《基本不等式》课件（苏教版必修5）

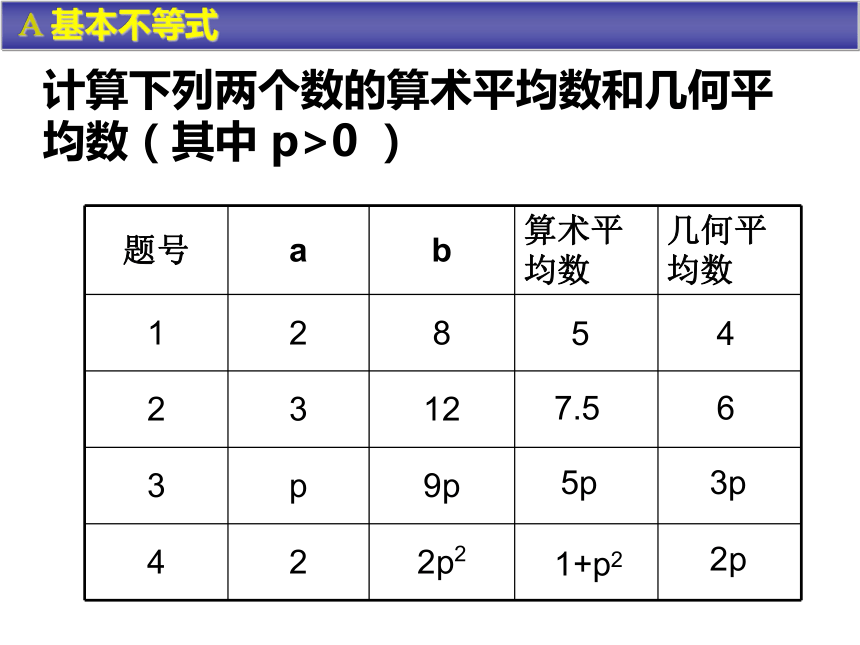
课件11张PPT。课题: §3.4基本不等式 第一课时 A 基本不等式某金店有一不准确的天平（臂长不等），你要买一串金项链，店主分别把项链放于左右两盘各称一次，分别称得a和b，然后把两次称得重量的算术平均数作为项链的重量,你认为这种称法是否合理？l1l2 A 基本不等式×问题情境 用一个两臂长短有差异的天平能否称得物体的实际重量呢？ A 基本不等式两个正数a,b的算术平均数两个正数a,b的几何平均数 A 基本不等式 A 基本不等式计算下列两个数的算术平均数和几何平均数（其中 p>0 ）547.565p3p1+p22p猜一猜：两个正数a.b的算术平均数和几何平均数之间具有怎样的大小关系？试试看猜猜看即：两个正数的几何平均数不大于它们的算术平均数，当两个数相等时相等。 A 基本不等式（当且仅当a=b时，取“=”号）
几何解释：
半径不小于半弦 A 一个公式的应用-----称为基本不等式例1 已知a、b都是正数，求证： A 基本不等式已知a、b、c都是正数，求证 (a＋b)(b＋c)(c＋a)≥８abc练一练： A 基本不等式两正数a、b的
算术平均数：( )
几何平均数：( )
及它们的关系：随堂小结：当两个数相等时相等。 A 基本不等式再见