《二元一次不等式表示的平面区域》课件(苏教版必修5)
文档属性
| 名称 | 《二元一次不等式表示的平面区域》课件(苏教版必修5) |  | |
| 格式 | rar | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-24 11:38:00 | ||
图片预览





文档简介
课件14张PPT。二元一次不等式
表示的平面区域江苏省常熟中学高一数学备课组教学要求1. 理解二元一次不等式所表示的平面区域的含义;2. 学会用“选点法”判断不等式kx+b>0和kx+b<0所表示的平面区域。 在平面直角坐标系中,以二元一次方程:x-y+1=0 的解为坐标的点的集合是一条直线,那么以二元一次不等式的解为坐标的点的集合是什么图形?问题:在平面直坐标系中,
点集{ (x, y)| x>0 }表示什么图形?
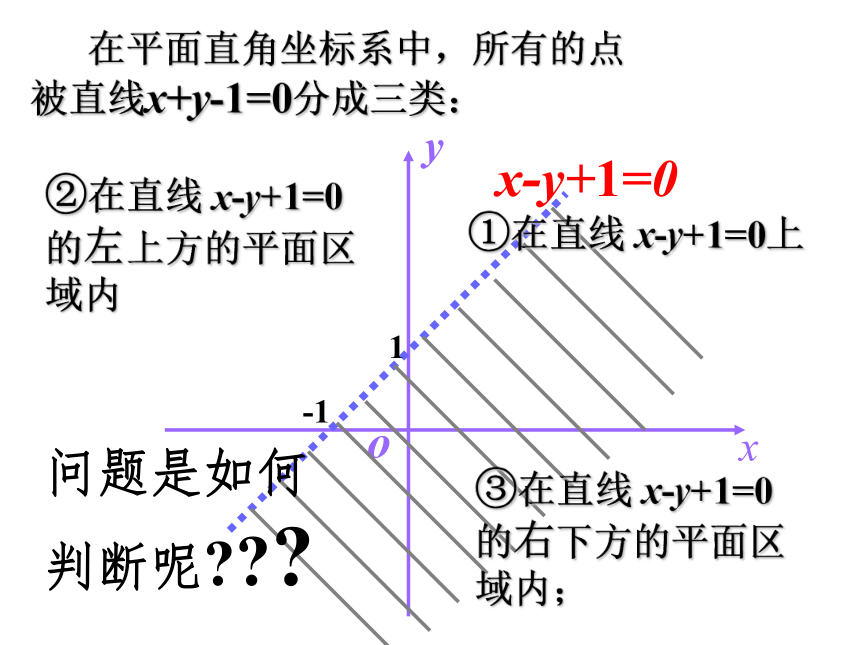
点集{ (x, y)| x<0 }呢? { (x, y)| y>0 }呢?{ (x, y)| x-y+1>0 }呢?1-1x-y+1=0 在平面直角坐标系中,所有的点
被直线x+y-1=0分成三类:①在直线 x-y+1=0上③在直线 x-y+1=0 的右下方的平面区域内;②在直线 x-y+1=0 的左上方的平面区域内问题是如何判断呢???1-1x-y+1>0x-y+1=00-0+1=1>0在直线: x-y+1=0右下方取原点代入:x-y+1
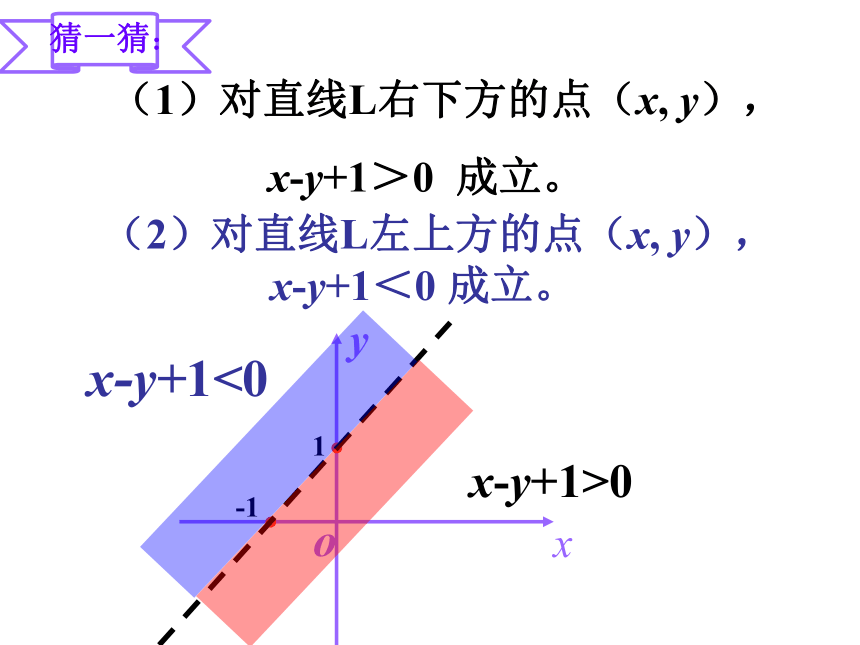
尝试? (1)对直线L右下方的点(x, y),
x-y+1>0 成立。 (2)对直线L左上方的点(x, y),x-y+1<0 成立。1-1x-y+1>0x-y+1<0(1)二元一次不等式Ax+By+C>0在平面直角坐标系中表示: 直线Ax+By+C=0某一侧所有点组成的平面区域。(2)在确定区域时,在直线的某一侧取一个特殊点(x0, y0) ,从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域。一般在C≠0时,取原点作为特殊点。得出结论:(3)注意所求区域是否包括边界直线例1 画出不等式
2x+y-6<0
表示的平面区域。362x+y-6<02x+y-6=0
巩固: 画出下列不等式表示的平面区域:
(1) x-y+1<0 (2) 2x+3y-6>0
(3) 2x+5y-10≥0 (4) 4x-3y≤12 解:不等式x-y+5>0表示
直线x-y+5=0上及右下方的点的集合,x+y≥0表示直线x+y=0
上及右上方的点的集合,x≤3表示直线x=3上及
左方的点的集合。 x+y=0x-y+5=0x=3所以,不等式所表示的平面区域如图所示巩固:画出下列不等式组表示的平面区域:应该注意的几个问题:1、若不等式中不含0,则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。否则应画成实线。变式一:
画出不等式 (x+2y+1) (x-y+4) < 0
表示的平面区域.变式二:
由直线 x+y+2=0, x+2y+1=0和
2x+y+1=0围成的三角形(包括边界)
用不等式可表示为变式三:求不等式|x-2|+|y-2|≤2
所表示的平面区域的面积
表示的平面区域江苏省常熟中学高一数学备课组教学要求1. 理解二元一次不等式所表示的平面区域的含义;2. 学会用“选点法”判断不等式kx+b>0和kx+b<0所表示的平面区域。 在平面直角坐标系中,以二元一次方程:x-y+1=0 的解为坐标的点的集合是一条直线,那么以二元一次不等式的解为坐标的点的集合是什么图形?问题:在平面直坐标系中,
点集{ (x, y)| x>0 }表示什么图形?
点集{ (x, y)| x<0 }呢? { (x, y)| y>0 }呢?{ (x, y)| x-y+1>0 }呢?1-1x-y+1=0 在平面直角坐标系中,所有的点
被直线x+y-1=0分成三类:①在直线 x-y+1=0上③在直线 x-y+1=0 的右下方的平面区域内;②在直线 x-y+1=0 的左上方的平面区域内问题是如何判断呢???1-1x-y+1>0x-y+1=00-0+1=1>0在直线: x-y+1=0右下方取原点代入:x-y+1
尝试? (1)对直线L右下方的点(x, y),
x-y+1>0 成立。 (2)对直线L左上方的点(x, y),x-y+1<0 成立。1-1x-y+1>0x-y+1<0(1)二元一次不等式Ax+By+C>0在平面直角坐标系中表示: 直线Ax+By+C=0某一侧所有点组成的平面区域。(2)在确定区域时,在直线的某一侧取一个特殊点(x0, y0) ,从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域。一般在C≠0时,取原点作为特殊点。得出结论:(3)注意所求区域是否包括边界直线例1 画出不等式
2x+y-6<0
表示的平面区域。362x+y-6<02x+y-6=0
巩固: 画出下列不等式表示的平面区域:
(1) x-y+1<0 (2) 2x+3y-6>0
(3) 2x+5y-10≥0 (4) 4x-3y≤12 解:不等式x-y+5>0表示
直线x-y+5=0上及右下方的点的集合,x+y≥0表示直线x+y=0
上及右上方的点的集合,x≤3表示直线x=3上及
左方的点的集合。 x+y=0x-y+5=0x=3所以,不等式所表示的平面区域如图所示巩固:画出下列不等式组表示的平面区域:应该注意的几个问题:1、若不等式中不含0,则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。否则应画成实线。变式一:
画出不等式 (x+2y+1) (x-y+4) < 0
表示的平面区域.变式二:
由直线 x+y+2=0, x+2y+1=0和
2x+y+1=0围成的三角形(包括边界)
用不等式可表示为变式三:求不等式|x-2|+|y-2|≤2
所表示的平面区域的面积
