一次函数练习
图片预览



文档简介
一次函数练习
1、列出下列函数关系式,判别其中哪些为一次函数、正比例函数. ( http: / / www. )
(1)正方形周长p和一边的长a. (2)圆的面积A与半径R. (3)长a一定时矩形面积y与宽x. ( http: / / www. )
(4)15斤梨售价20元.售价y与斤数x. (5)定期存100元本金,月利率1.8%,本息y与所存月数x. ( http: / / www. )
(6)水库原存水Q立方米,现以每小时a立方米的流量开闸放水,同时上游以每小时b立方米的流量向水库注水,求这时水库的蓄水量M与时间t的函数关系.
2、已知y+a与x+b(a,b是常数)成正比例,
(1)y是x的一次函数吗?请说明理由;(2)在什么条件下,y是x的正比例函数?
3、如果 为一次函数,且不是正比例函数,则m、n关系?
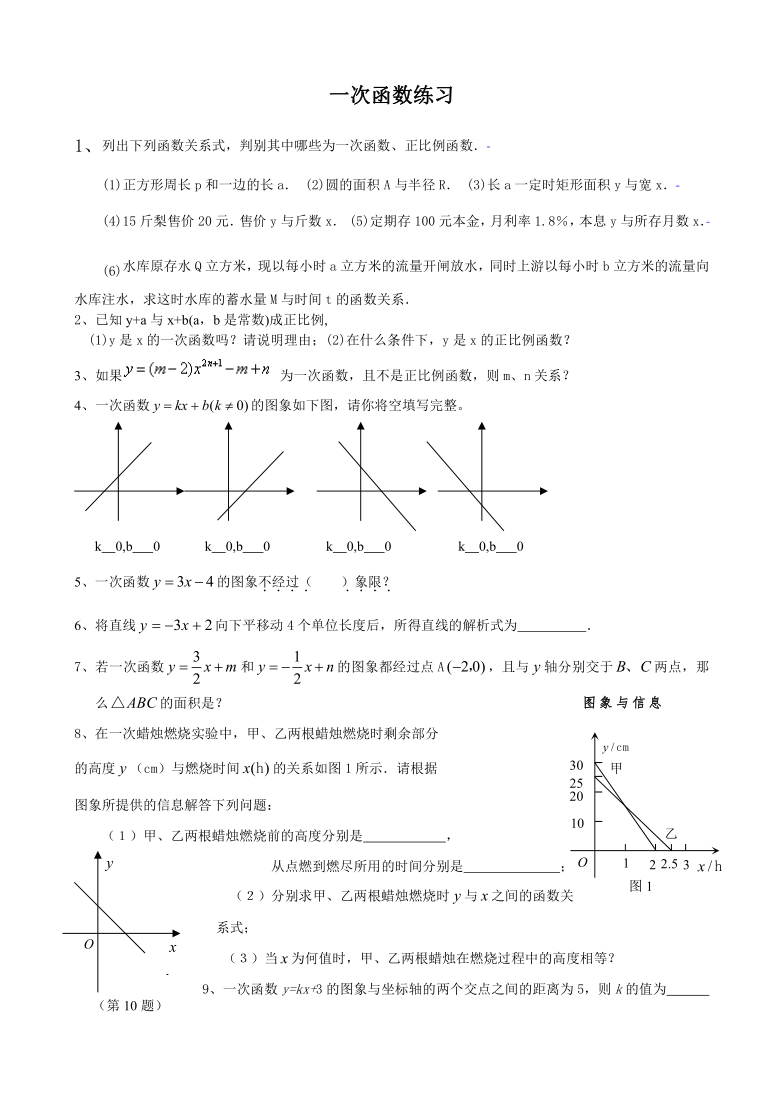
4、一次函数的图象如下图,请你将空填写完整。
5、一次函数的图象不经过( )象限?
6、将直线向下平移动4个单位长度后,所得直线的解析式为 .
7、若一次函数和的图象都经过点A,且与轴分别交于两点,那么的面积是?
8、在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分
的高度(cm)与燃烧时间的关系如图1所示.请根据
图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,
从点燃到燃尽所用的时间分别是 ;
(2)分别求甲、乙两根蜡烛燃烧时与之间的函数关
系式;
(3)当为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
9、一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5,则k的值为
10、直线如图所示,化简: .
11、如图,表示一次函数与正比例函数(为常数,且
)图象的是( )
12、在下列函数中,( )的函数值先达到100.
A. B. C. D.
13、已知一次函数与一次函数,若它们的图象是两条互相平等的直线,则 .
14、已知一次函数,且的值随值的增大而增大.
(1)的范围;(2)若此一次函数又是正比例函数,试求的值.
15、若函数与轴的交点在轴的上方,且为整数,则符合条件的有( )A.8个 B.7个 C.9个 D.10个
16、已知一次函数的图象经过一、二、四象限,求的取值范围.
17、求过点且与已知直线平行的直线的函数表达式,并画出直线 的图象;
(1)设直线分别与轴、轴交于点、,如果直线:与直线平行且交轴于点,求出△的面积关于的函数表达式.
18、在平面直角坐标中,边长为2的正方形的两顶点、分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转,当点第一次落在直线上时停止旋转,旋转过程中,边交直线于点,边交轴于点(如图).
(1)求边在旋转过程中所扫过的面积;
(2)旋转过程中,当和平行时,求正方形
旋转的度数;
(3)设的周长为,在旋转正方形
的过程中,值是否有变化?请证明你的结论.
19:某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金元,要使(2)中所有方案获利相同,值应是多少?此时,哪种方案对公司更有利?
20、某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元)和蔬菜加工厂自己加工制作纸箱的费用(元)关于(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
21、某冰箱厂为响应国家“家电下乡”号召,计划生产、两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
型号 A型 B型
成本(元/台) 2200 2600
售价(元/台) 2800 3000
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
22、如图,直线与两坐标轴分别相交于A.B点,点M是线段AB上任意一点(A.B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式
23、在直角坐标系中直接画出函数的图象;若一次函数的图象分别过点,,请你依据这两个函数的图象写出方程组的解.
24、“六一”前夕,某玩具经销商用去2350元购进A.B.C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具套,B种玩具套,三种电动玩具的进价和售价如右表所示,
型 号 A B C
进价(元/套) 40 55 50
售价(元/套) 50 80 65
⑴用含、的代数式表示购进C种玩具的套数;
⑵求与之间的函数关系式;
⑶假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元。
①求出利润P(元)与(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套。
25、为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元?
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买支钢笔需要花元,请你求出与的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.
答案
1:(1)∵p=4a.自变量a为一次且其系数为4(不为零).∴p为a的一次函数.又∵不含常数项所以也是正比例函数.正方形边长a>0 (2) ,自变量R的次数是二次,所以不是一次函数,也不是正比例函数. (3)y=ax,自变量x为一次且系数a为长度(不为零).∴y是x的一次函数.∵不含常数项.∴y也是x的正比例函数.矩形的宽0<x<a.(4) ,自变量x为一次,又系数 . 是一次函数,也是正比例函数。梨的斤数x≥0 (5)y=100+100×1.8%x,自变量x的次数为一次,又含有常数项.∴y是x的一次函数但不是正比例函数.所存月数x≥0 (6)M=Q+(b-a)t,因为自变量t的次数为一次,当a≠b时,M是t的一次函数.若Q=0时,M是t的正比例函数;若a=b时,M是常量函数,不是t的一次函数. HYPERLINK "http://www." 注放水时间t,当 时, ,当 时与水库可存水量有关。
2:1)y是x的一次函数.∵y+a与x+b是正比例函数,∴设y+a=k(x+b)(k为常数,且k≠0).整理,得y=kx+(kb-a).∵k≠0,k,a,b为常数,∴y=kx+(kb-a)是一次函数.(2)当kb-a=0,即a=kb时,y是x的正比例函数. 3: 5:第二象限 6:
7:4 8:(1)30cm,25cm;2h,2.5h;(2)设甲蜡烛燃烧时与之间函数关系式为,
由图可知,函数的图象过点(2,0)、(0,30),
解得
设乙蜡烛燃烧时与之间的函数关系式为,
由图可知,函数的图象过点(2.5,0)、(0,25),
解得
(3)由题意得 ,解得.
当甲、乙两根蜡烛燃烧1h的时候高度相等.
9:或 10: 11:C 12:B 13:3 14:解:(1)由题意,得,所以;
(2)由题意,得,所以.又因为,所以的值为4.即当时,
此函数是正比例函数,且随值的增大而增大.
15:B 16:的取值范围是. 17:直线l的函数表达式为y=—2x+6.
(1)∴C点在x轴的正半轴上.
当C点在B点的左侧时,;(0<t<6
当C点在B点的右侧时, .(t>6
18:1)解:∵点第一次落在直线上时停止旋转,
∴旋转了.∴在旋转过程中所扫过的面积为.
(2)解:∵∥,
∴,.∴.∴.
又∵,∴.又∵,,∴.
∴.∴.
∴旋转过程中,当和平行时,正方形旋转的度数为.
(3)答:值无变化.
证明:延长交轴于点,则,
,∴.
又∵,.∴.
∴.
又∵,,
∴.∴.
∴,
∴.
∴在旋转正方形的过程中,值无变化.
19:(1)设今年三月份甲种电脑每台售价元
解得: 经检验: 是原方程的根, 所以甲种电脑今年三月份每台售价4000元.
(2)设购进甲种电脑台,
解得 因的正整数为6,7,8,9,10, 有5种进货方案
(3) 设总获利为元,
当时, (2)中所有方案获利相同. 此时, 购买甲种电脑6台,乙种电脑9台时对公司更有利.
20:(1)从纸箱厂定制购买纸箱费用: 蔬菜加工厂自己加工纸箱费用:.
(2),由,得:,
解得:. 当时,,选择方案一,从纸箱厂定制购买纸箱所需的费用低.
当时,,选择方案二,蔬菜加工厂自己加工纸箱所需的费用低.
当时,,两种方案都可以,两种方案所需的费用相同.
21:(1)设生产型冰箱台,则型冰箱为台,由题意得:
解得: x是正整数 取38,39或40.
有以下三种生产方案:
方案一 方案二 方案三
A型/台 38 39 40
B型/台 62 61 60
(2)设投入成本为元,由题意有:
随的增大而减小当时,有最小值.
即生产型冰箱40台,型冰箱50台,该厂投入成本最少
此时,政府需补贴给农民
(3)实验设备的买法共有10种.
22:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(00,-x+4>0);
则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;
∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8
∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;
(2)根据题意得:S四边形OCMD=MC·MD=(-x+4)· x=-x2+4x=-(x-2)2+4
∴四边形OCMD的面积是关于点M的横坐标x(0(3)如图(2),当时,;
如图(3),当时,;
23:
24:1)购进C种玩具套数为:50-x-y(或47-x-y)
(2)由题意得 整理得
(3)①利润=销售收入-进价-其它费用
又∵ ∴整理得
②购进C种电动玩具的套数为:
据题意列不等式组,解得 ∴x的范围为,且x为整数 的最大值是23∵在中,>0 ∴P随x的增大而增大
∴当x取最大值23时,P有最大值,最大值为595元.此时购进A.B.C种玩具分别为23套、16套、11套.
25:(1)解:设每个笔记本元,每支钢笔元. 解得
答:每个笔记本14元,每支钢笔15元.
(2)
(3)当时,;
当时,;
当时,.综上,当买超过10件但少于15件商品时,买笔记本省钱;
当买15件奖品时,买笔记本和钢笔一样;
当买奖品超过15件时,买钢笔省钱.
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
甲
乙
1
2
2.5
3
10
20
25
30
O
图象与信息
图1
(第10题)
O
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
O
A
B
C
M
N
O
A
B
C
M
N
B
x
y
M
C
D
O
A
图(1)
B
x
y
O
A
图(2)
B
x
y
O
A
图(3)
y
x
O
1
2
-1
1
2
1、列出下列函数关系式,判别其中哪些为一次函数、正比例函数. ( http: / / www. )
(1)正方形周长p和一边的长a. (2)圆的面积A与半径R. (3)长a一定时矩形面积y与宽x. ( http: / / www. )
(4)15斤梨售价20元.售价y与斤数x. (5)定期存100元本金,月利率1.8%,本息y与所存月数x. ( http: / / www. )
(6)水库原存水Q立方米,现以每小时a立方米的流量开闸放水,同时上游以每小时b立方米的流量向水库注水,求这时水库的蓄水量M与时间t的函数关系.
2、已知y+a与x+b(a,b是常数)成正比例,
(1)y是x的一次函数吗?请说明理由;(2)在什么条件下,y是x的正比例函数?
3、如果 为一次函数,且不是正比例函数,则m、n关系?
4、一次函数的图象如下图,请你将空填写完整。
5、一次函数的图象不经过( )象限?
6、将直线向下平移动4个单位长度后,所得直线的解析式为 .
7、若一次函数和的图象都经过点A,且与轴分别交于两点,那么的面积是?
8、在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分
的高度(cm)与燃烧时间的关系如图1所示.请根据
图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,
从点燃到燃尽所用的时间分别是 ;
(2)分别求甲、乙两根蜡烛燃烧时与之间的函数关
系式;
(3)当为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
9、一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5,则k的值为
10、直线如图所示,化简: .
11、如图,表示一次函数与正比例函数(为常数,且
)图象的是( )
12、在下列函数中,( )的函数值先达到100.
A. B. C. D.
13、已知一次函数与一次函数,若它们的图象是两条互相平等的直线,则 .
14、已知一次函数,且的值随值的增大而增大.
(1)的范围;(2)若此一次函数又是正比例函数,试求的值.
15、若函数与轴的交点在轴的上方,且为整数,则符合条件的有( )A.8个 B.7个 C.9个 D.10个
16、已知一次函数的图象经过一、二、四象限,求的取值范围.
17、求过点且与已知直线平行的直线的函数表达式,并画出直线 的图象;
(1)设直线分别与轴、轴交于点、,如果直线:与直线平行且交轴于点,求出△的面积关于的函数表达式.
18、在平面直角坐标中,边长为2的正方形的两顶点、分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转,当点第一次落在直线上时停止旋转,旋转过程中,边交直线于点,边交轴于点(如图).
(1)求边在旋转过程中所扫过的面积;
(2)旋转过程中,当和平行时,求正方形
旋转的度数;
(3)设的周长为,在旋转正方形
的过程中,值是否有变化?请证明你的结论.
19:某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金元,要使(2)中所有方案获利相同,值应是多少?此时,哪种方案对公司更有利?
20、某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元)和蔬菜加工厂自己加工制作纸箱的费用(元)关于(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
21、某冰箱厂为响应国家“家电下乡”号召,计划生产、两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
型号 A型 B型
成本(元/台) 2200 2600
售价(元/台) 2800 3000
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
22、如图,直线与两坐标轴分别相交于A.B点,点M是线段AB上任意一点(A.B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式
23、在直角坐标系中直接画出函数的图象;若一次函数的图象分别过点,,请你依据这两个函数的图象写出方程组的解.
24、“六一”前夕,某玩具经销商用去2350元购进A.B.C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具套,B种玩具套,三种电动玩具的进价和售价如右表所示,
型 号 A B C
进价(元/套) 40 55 50
售价(元/套) 50 80 65
⑴用含、的代数式表示购进C种玩具的套数;
⑵求与之间的函数关系式;
⑶假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元。
①求出利润P(元)与(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套。
25、为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件.小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求购买每个笔记本和钢笔分别为多少元?
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买支钢笔需要花元,请你求出与的函数关系式;
(3)在(2)的条件下,小明决定买同一种奖品,数量超过10个,请帮小明判断买哪种奖品省钱.
答案
1:(1)∵p=4a.自变量a为一次且其系数为4(不为零).∴p为a的一次函数.又∵不含常数项所以也是正比例函数.正方形边长a>0 (2) ,自变量R的次数是二次,所以不是一次函数,也不是正比例函数. (3)y=ax,自变量x为一次且系数a为长度(不为零).∴y是x的一次函数.∵不含常数项.∴y也是x的正比例函数.矩形的宽0<x<a.(4) ,自变量x为一次,又系数 . 是一次函数,也是正比例函数。梨的斤数x≥0 (5)y=100+100×1.8%x,自变量x的次数为一次,又含有常数项.∴y是x的一次函数但不是正比例函数.所存月数x≥0 (6)M=Q+(b-a)t,因为自变量t的次数为一次,当a≠b时,M是t的一次函数.若Q=0时,M是t的正比例函数;若a=b时,M是常量函数,不是t的一次函数. HYPERLINK "http://www." 注放水时间t,当 时, ,当 时与水库可存水量有关。
2:1)y是x的一次函数.∵y+a与x+b是正比例函数,∴设y+a=k(x+b)(k为常数,且k≠0).整理,得y=kx+(kb-a).∵k≠0,k,a,b为常数,∴y=kx+(kb-a)是一次函数.(2)当kb-a=0,即a=kb时,y是x的正比例函数. 3: 5:第二象限 6:
7:4 8:(1)30cm,25cm;2h,2.5h;(2)设甲蜡烛燃烧时与之间函数关系式为,
由图可知,函数的图象过点(2,0)、(0,30),
解得
设乙蜡烛燃烧时与之间的函数关系式为,
由图可知,函数的图象过点(2.5,0)、(0,25),
解得
(3)由题意得 ,解得.
当甲、乙两根蜡烛燃烧1h的时候高度相等.
9:或 10: 11:C 12:B 13:3 14:解:(1)由题意,得,所以;
(2)由题意,得,所以.又因为,所以的值为4.即当时,
此函数是正比例函数,且随值的增大而增大.
15:B 16:的取值范围是. 17:直线l的函数表达式为y=—2x+6.
(1)∴C点在x轴的正半轴上.
当C点在B点的左侧时,;(0<t<6
当C点在B点的右侧时, .(t>6
18:1)解:∵点第一次落在直线上时停止旋转,
∴旋转了.∴在旋转过程中所扫过的面积为.
(2)解:∵∥,
∴,.∴.∴.
又∵,∴.又∵,,∴.
∴.∴.
∴旋转过程中,当和平行时,正方形旋转的度数为.
(3)答:值无变化.
证明:延长交轴于点,则,
,∴.
又∵,.∴.
∴.
又∵,,
∴.∴.
∴,
∴.
∴在旋转正方形的过程中,值无变化.
19:(1)设今年三月份甲种电脑每台售价元
解得: 经检验: 是原方程的根, 所以甲种电脑今年三月份每台售价4000元.
(2)设购进甲种电脑台,
解得 因的正整数为6,7,8,9,10, 有5种进货方案
(3) 设总获利为元,
当时, (2)中所有方案获利相同. 此时, 购买甲种电脑6台,乙种电脑9台时对公司更有利.
20:(1)从纸箱厂定制购买纸箱费用: 蔬菜加工厂自己加工纸箱费用:.
(2),由,得:,
解得:. 当时,,选择方案一,从纸箱厂定制购买纸箱所需的费用低.
当时,,选择方案二,蔬菜加工厂自己加工纸箱所需的费用低.
当时,,两种方案都可以,两种方案所需的费用相同.
21:(1)设生产型冰箱台,则型冰箱为台,由题意得:
解得: x是正整数 取38,39或40.
有以下三种生产方案:
方案一 方案二 方案三
A型/台 38 39 40
B型/台 62 61 60
(2)设投入成本为元,由题意有:
随的增大而减小当时,有最小值.
即生产型冰箱40台,型冰箱50台,该厂投入成本最少
此时,政府需补贴给农民
(3)实验设备的买法共有10种.
22:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0
则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;
∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8
∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;
(2)根据题意得:S四边形OCMD=MC·MD=(-x+4)· x=-x2+4x=-(x-2)2+4
∴四边形OCMD的面积是关于点M的横坐标x(0
如图(3),当时,;
23:
24:1)购进C种玩具套数为:50-x-y(或47-x-y)
(2)由题意得 整理得
(3)①利润=销售收入-进价-其它费用
又∵ ∴整理得
②购进C种电动玩具的套数为:
据题意列不等式组,解得 ∴x的范围为,且x为整数 的最大值是23∵在中,>0 ∴P随x的增大而增大
∴当x取最大值23时,P有最大值,最大值为595元.此时购进A.B.C种玩具分别为23套、16套、11套.
25:(1)解:设每个笔记本元,每支钢笔元. 解得
答:每个笔记本14元,每支钢笔15元.
(2)
(3)当时,;
当时,;
当时,.综上,当买超过10件但少于15件商品时,买笔记本省钱;
当买15件奖品时,买笔记本和钢笔一样;
当买奖品超过15件时,买钢笔省钱.
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
甲
乙
1
2
2.5
3
10
20
25
30
O
图象与信息
图1
(第10题)
O
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
O
A
B
C
M
N
O
A
B
C
M
N
B
x
y
M
C
D
O
A
图(1)
B
x
y
O
A
图(2)
B
x
y
O
A
图(3)
y
x
O
1
2
-1
1
2
