苏教版数列课件

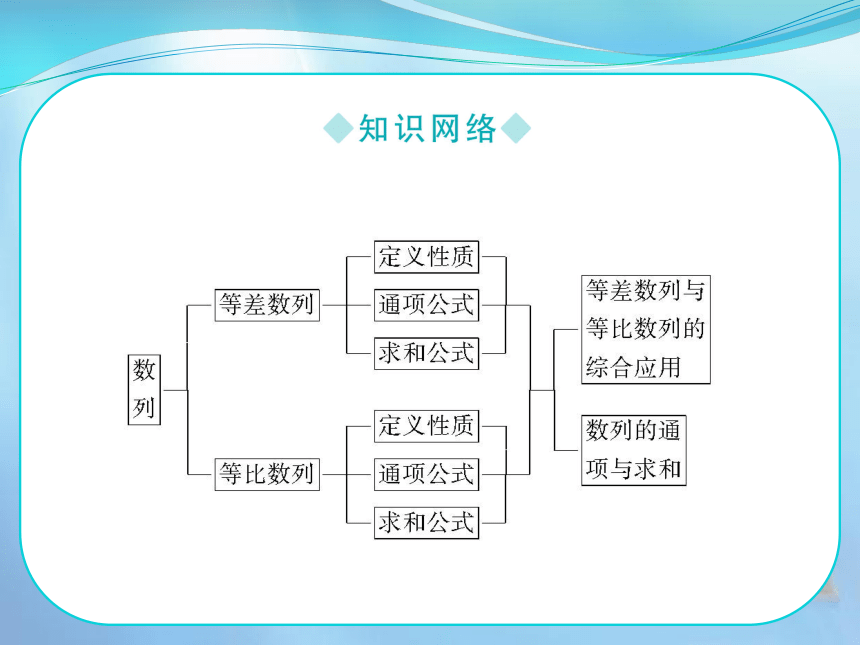
课件122张PPT。 等差、等比数列是两种最基本、最常见的数列，灵活地运用等差、等比数列的性质，能使问题简化；灵活地运用通项公式和前n项和公式解题是高考考查的重点．从等差数列中按某种规律，抽取某些项，依次排列，组成一个等比数列，是等差、等比数列综合题中的较重要的类型，要认真体会此类题．用函数的观点和方法揭示等差数列和等比数列的特征，在分析和解决有关数列的综合题中具有重要的意义．复习时，要注意以下几点：一是深刻理解等差数列与等比数列的定义及等价形式，灵活运用等差数列、等比数列的性质．二是注意方程思想、整体思想、分类讨论思想、数形结合思想的运用．第一节　等差数列1．等差数列的概念
若数列{an}从 起，每一项与它的 的差等于同一个 ，
则数列{an}叫等差数列．
2．通项公式：an＝ ，
若d≠0，表示an是n的 函数；若d＝0，表示此数列为 第二项前一项常数a1＋(n－1)d一次常数列推广：an＝am＋ .
对于 数列{an}，若n＋m＝p＋q，则 .
4．前n项和：
5．等差数列{an}中，当a1＜0，d＞0时，数列{an}为 数列，Sn有最小值；当a1＞0，d＜0时，数列{an}为 数列，Sn有最 值；当d＝0时，{an}为 数列．
an＋am＝ap＋aq等差(n－m)d递减大常递增若数列{an}是等差数列，Sn是其前n项的和，k∈N*，那么Sk，S2k－Sk，S3k－S2k成 数列．
等差6．奇数项和与偶数项和的关系
设数列{an}是等差数列，S奇是奇数项的和，S偶是偶数项的和，Sn是前n项的和，则有如下性质：前n项的和Sn＝S奇＋S偶．
当n为偶数时，S偶－S奇＝ d，其中d为公差；
当n为奇数时，则S奇－S偶＝a中，S奇＝ a中，1．已知{an}为等差数列，a3＋a8＝22，a6＝7，则a5＝________________________________________________________________________.
2．已知{an}是等差数列，a1＋a2＝4，a7＋a8＝28，，则该数列前10项和S10＝________.【解析】　a3＋a8＝a5＋a6，
∴a5＝a3＋a8－a6＝22－7＝15.
【答案】　15【答案】　100
3．等差数列{an}的前n项和为Sn，且6S5－5S3＝5，则a4＝________.【答案】　49【解析】因此Sn＝－8n＋n(n－1)＝n(n－9)或Sn＝8n－n(n－1)＝－n(n－9)． 数阵问题
近年来，数表问题频频出现在高考试题中，它与数列知识联手奏出一曲曲优美的“乐章”．它主要考查等差数列(有时可能为等比数列，多数是等差数列)的通项公式、求和公式以及性质的灵活运用．　下表给出一个“等差数阵”：其中每行、每列都是等差数列，aij表示位于第i行第j列的数．
(1)写出a45的值；
(2)写出aij的计算公式以及2 008在等差数阵中所在的一个位置．
【点拨】　本题主要考查等差数列的通项公式，以及知道项求项数的问题 【解】　(1)a45＝49.当i＝1时，得j＝669，所以2 008在等差数阵中的一个位置是第1行第669列．在等差数列{an}中，当a1<0，d＞0时，数列{an}为增数列，Sn有最小值；当a1＞0，d＜0时，数列{an}为减数列，Sn有最大值．在等差数列{an}中，满足3a4＝7a7，且a1>0，Sn是数列{an}前n项的和，若Sn取得最大值，求n的值．
【点拨】　若an≥0且an＋1＜0，Sn取得最大值，或利用等差数列{an}中前n和Sn是关于n的二次函数的形式，可以利用二次函数求最值，但此时要注意n的值为整数．
【解】　解法一　设公差为d，由题设有3(a1＋3d)＝7(a1＋6d)，最值问题Sn与an的关系(2)求an的表达式．求证数列{bn}是等差数列，并求数列{an}的通项公式．(本题满分16分)已知a为实数，数列{an}满足a1＝a，当n≥2时，数列的综合题是高考重点考查对象，与等差数列有关的解答题，重点考查函数与方程、不等式、等价转化等思想方法的灵活运用．(本题满分16分)已知a为实数，数列{an}满足a1＝a，当n≥2时，【点拨】　数列{an}是分段数列的形式，因此要注意分段求解，分组求和．由于bn中含有(－1)n，因此要注意将n按奇数、偶数进行分类讨论．(1)【解】　当a＝100时，由题意知数列{an}的前34项成首项为100，公差为－3的等差数列，从第35项开始，奇数项均为3，偶数项均为1，从而(2)【证明】　①若0②若a1>3，此时数列{an}的前若干项满足an－an－1＝3，即an＝a1－3(n－1)．
设a1∈(3k,3k＋3]，(k≥1，k∈N*)，则当n＝k＋1时，ak＋1＝a1－3k∈(0,3]．从而此时命题成立；(8分)③若a1≤0，由题意得a2＝4－a1>3，则由②的结论知此时命题也成立．
综上所述，原命题成立．(10分)已知{an}是一个公差大于0的等差数列，且满足a3a6＝55，a2＋a7＝16.由①得2a1＝16－7d将其代入②得(16－3d)(16＋3d)＝220.即256－9d2＝220
∴d2＝4，又d>0，∴d＝2，代入①得a1＝1
∴an＝1＋(n－1)·2＝2n－1.【解】　(1)设等差数列{an}的公差为d，则依题设d>0
由a2＋a7＝16.得2a1＋7d＝16①
由a3·a6＝55，得(a1＋2d)(a1＋5d)＝55②规律总结复习时要注意以下几点：深刻理解等差数列的定义及等价形式；由五个量a1，d，n，an，Sn中的三个量可求出其余两个量，要求选用公式要恰当，即善于减少运算量，达到快速、准确的目的；已知三个或四个数成等差数列这类问题，要善于设元，目的仍在于减少运算量，如三个数成等差数列时，除了设a，a＋d，a＋2d外，还可设a－d，a，a＋d；四个数成等差数列时，可设为a－3d，a－d，a＋d，a＋3d.【解】　(1)设公差为d，则a－a＝a－a，由性质得－3d(a4＋a3)＝d(a4＋a3)，因为d≠0，所以a4＋a3＝0，即2a1＋5d＝0，又由S7＝7得
，解得a1＝－5，d＝2，所以{an}的通项公式为an＝2n－7，前n项和Sn＝n2－6n.所以满足条件的正整数m＝2.则2m－3必是8的约数且m∈N*，故m＝1，所以要想得满分还是不易．【命题趋势】　近几年来江苏高考一直将数列问题作为压轴题来进行命题，往往难度大，不少学生基本不得分.2011年高考很有可能回归教材和重视基础知识、基本方法基本技能，重视两纲的导向作用，会有意识降低难度．学而时习之，不亦说乎？第二节　等比数列1．等比数列的概念：如果一个数列从第二项起，每一项与它的 等于同一个常数，那么这个数列就叫做等比数列．这个常数叫做等比数列的公比，用q表示(q≠0)．前一项的比等比G2＝abanan＋2＝a2n+1an＝a1qn－1an＝amqn－mmna1对于等比数列{an}，若n＋m＝u＋v，则 ，也就是：a1·an＝a2·an－1＝a3·an－2＝….
若数列{an}是等比数列，Sn是其前n项的和，k∈N*，那么Sk，S2k－Sk，S3k－S2k成 数列．an·am＝au·av等比1．若数列{an}满足：a1＝1，an＋1＝2an(n∈N*)，则a5＝________；前8项的和S8＝________.(用数字作答)【解析】　由a2＋a3＝q(a1＋a2)＝3q＝6，∴q＝2，∴a1(1＋q)＝3，∴a1＝1，∴a7＝26＝64.
【答案】　64
3．设等比数列{an}的公比q＝ ，前n项和为Sn，则 ＝________.6．已知{an}为等比数列，a3＝2，a2＋a4＝ ，求{an}的通项公式．通项公式灵活运用等比数列的通项公式与定义式，可以简化运算，提高解题速度及准确性．
　已知等比数列{an}中，a2＝2，a5＝128.
(1)求通项an；
(2)若bn＝log2an，数列{bn}的前n项和为Sn，且Sn＝360，求n的值．【点拨】　本题可以利用等比数列的通项公式，也可以利用推广公式a5＝a2q3.
【解】　(1)设等比数列{an}的公比为q，则求和公式在求等比数列前n项和时，若公比q用一个字母表示时，一定要注意对公比q进行讨论，即分公比q等于1和不等于1两种情况讨论．【点拨】　本题如果利用求和公式求解，需对公比q是否为1进行讨论，而要抓住条件中S30，S20，S10的特点，可以采用整体思想求解，避免求和公式出现，无需讨论公比是否为1.新数列问题近年来构造新数列，是高考数列命题的一个热点，解决这类问题主要是抓住等差数列、等比数列的定义、通项公式、性质、求和公式，进行重新构造，它们实际上是等差数列与等比数列的灵活运用．
　(2009·全国卷Ⅱ)设数列{an}的前n项和为Sn，已知a1＝1，Sn＋1＝4an＋2.
(1)设bn＝an＋1－2an，证明数列{bn}是等比数列；(2)求数列{an}的通项公式．【点拨】　第(1)问思路明确，只需利用已知条件寻找bn与bn－1的关系即可．第(2)问中由(1)易得an＋1－2an＝3·2n－1，这个递推式明显是一个构造新数列的模型：an＋1＝pan＋qn(p，q为常数)，主要的处理手段是两边除以qn＋1.(1)【证明】　由a1＝1，及Sn＋1＝4an＋2，
有a1＋a2＝4a1＋2，a2＝3a1＋2＝5，∴b1＝a2－2a1＝3
由Sn＋1＝4an＋2， ①
则当n≥2时，有Sn＝4an－1＋2②
①－②得an＋1＝4an－4an－1，∴an＋1－2an＝2(an－2an－1)
又∵bn＝an＋1－2an，∴bn＝2bn－1
∴{bn}是首项b1＝3，公比为2的等比数列．数列{an}的前n项和Sn满足：Sn＝2an－3n(n∈N*)．
(1)证明：数列{an＋3}是等比数列；
(2)求数列{an}的通项公式an.(1)【证明】　当n∈N*时有：Sn＝2an－3n，
∴Sn＋1＝2an＋1－3(n＋1)，
两式相减得：an＋1＝2an＋1－2an－3，∴an＋1＝2an＋3，
∴an＋1＋3＝2(an＋3)，∴数列{an＋3}是首项为6，公比为2的等比数列．
(2)【解】　又a1＝S1＝2a1－3，
∴a1＝3，a1＋3＝6≠0.
从而an＋3＝6·2n－1，∴an＝3·2n－3.等比数列的判断等比数列是比相等，它暗含了等比数列的每一项都不为0，且公比也不为0，它与an＝an－1q并不等价，因为后者an与q可以为0.(1)当m＝1时，求证：对于任意的实数λ，{an}一定不是等差数列；
(2)当λ＝－时，试判断{bn}是否为等比数列；
(3) 设Sn为数列{bn}的前n项和，在(2)的条件下，是否存在实数m，使得对任意的正整数n，都有 ≤Sn≤ ？若存在，请求出m的取值范围；若不存在，请说明理由．【点拨】　证明等比数列一要证明公比为常数，二是要证明首项不为0.1)【证明】　当m＝1时，a1＝1，a2＝λ＋1，a3＝λ2＋λ＋2(2分)
假设{an}是等差数列，由a1＋a3＝2a2得λ2＋λ＋3＝2(λ＋1)，即λ2－λ＋1＝0，
∵△＝1－4＝－3<0，方程无解．
故对于任意的实数λ，{an}一定不是等差数列．…(4分)规律总结求解等比数列有关问题的常见思想方法有：一是方程的思想．等比数列中有五个量a1、n、q、an和Sn，通常可以知三求二，通过列方程组求关键量a1与q.二是分类讨论思想．当等比数列的公比没有说明是否为1时，求Sn需要讨论．另外，通过对首项和公比的讨论，还会知道等比数列的类型等等．(2009·天津卷)已知等差数列{an}的公差为d(d≠0)，等比数列{bn}的公比为q(q>1)．设Sn＝a1b1＋a2b2…＋anbn，Tn＝a1b1－a2b2＋…＋(－1)n－1anbn，n∈N*【点拨】　本小题主要考查等差数列的通项公式、等比数列的通项公式与前n项和公式等基础知识，考查运算能力，推理论证能力及综合分析和解决问题的能力．
(1)【解】　由题设，可得an＝2n－1，bn＝3n－1，n∈N*
∴S3＝a1b1＋a2b2＋a3b3＝1×1＋3×3＋5×9＝55(2)【证明】　由题设可得bn＝qn－1则
S2n＝a1＋a2q＋a3q2＋…＋a2nq2n－1，①
T2n＝a1－a2q＋a3q2－a4q3＋…－a2nq2n－1，②
①式减去②式，得： 【误区警示】　本题难就难在对Sn＝a1b1＋a2b2…＋anbn，Tn＝a1b1－a2b2＋…＋(－1)n－1anbn，n∈N＋的处理上，由bn＝qn－1，不少学生不会对Sn与Tn进行合理的变形，即用方程组的思想来解决问题． 【命题趋势】　等差数列与等比数列的综合题是高考的热点，旨在考查将数列的知识实现相互的沟通，提升了对综合能力的考查．另外，运用方程思想求解数列题，特别是含有字母的问题，倍受高考的关注是高考考查的重点学而时习之，不亦说乎？第三节　数列求和2．求通项常用方法3．数列前n项和常用求法
(1)公式法：适用于等差、等比数列或可转化为等差、等比数列的数列．
(2)倒序相加法：类似于等差数列 公式的推导方法．
(3)裂项求和法：如果一个数列的每一项都能化为两项之差，并且前一项的减数恰与后一项的被减数 ，求和时中间项相互抵消．(4)错位相减法：适用于{anbn}，其中{an}是 数列，前n项和相同等差{bn}是 数列．
(5)分组求和法：将各项分解成 数列或 数列的和，分别求出这两个数列的和．等 比等差等比【答案】　992．如果数列{an}满足a1，a2－a1，a3－a2，…an－an－1，…是首项为1，公比为3的等比数列，则an＝________.【答案】　an＝2×3n6．已知数列{f(n)}的前n项和为Sn，且Sn＝n2＋2n.
(1)求数列{f(n)}的通项公式；
(2)若a1＝f(1)，an＋1＝f(an)(n∈N*)，求证数列{an＋1}是等比数列，并求数列{an}的前n项和Tn.【解】　(1)n≥2时，f(n)＝Sn－Sn－1＝2n＋1.
n＝1时，f(1)＝S1＝3，适合上式，∴f(n)＝2n＋1(n∈N*)．
(2)a1＝f(1)＝3，an＋1＝2an＋1(n∈N*)，即an＋1＋1＝2(an＋1)．
∴数列{an＋1}是首项为4、公比为2的等比数列．
an＋1＝(a1＋1)·2n－1＝2n＋1，∴an＝2n＋1－1(n∈N*)．
Tn＝(22＋23＋…＋2n＋1)－n＝2n＋2－4－n(n∈N*)．求数列通项公式，往往通过对数列若干项的观察、分析，猜想其通项公式，或利用an＝Sn－Sn－1(n≥2)来求通项公式，常见的类型为叠加法与叠乘法．【点拨】　形如an＋1＝an＋f(n)可采用叠加法；形如an＋1＝f(n)an常采用叠乘法；形如an＋1＝kan＋b(k、b为常数)常转化成等比数列来求．【解】　(1)∵an＋1＝an＋2n，∴an＋1－an＝2n，
∴an＝a1＋(a2－a1)＋(a3－a2)＋…＋(an－an－1)
＝1＋2×1＋2×2＋…＋2×(n－1)
＝1＋n×(n－1)＝n2－n＋1.裂项法裂项法的实质是将数列中的每项(通项)分解，然后重新组合，使之能消去一些项，最终达到求和的目的．【点拨】　数列求和的关键是分析通项，本题先要对通项进行分离常数，而后再进行“差分”，即裂项相消求和．分组求和对于既不是等差数列，又不是等比数列的类型，往往采用分组求和法．将此数列适当地拆开，可分成几个等差、等比数列或其它常见数列，然后分别求和，再将其合并．【点拨】　将每一项第一个数放在一起，再将每一项第二个数放在一起，这样形成两个组，然后分别求和，第一组求和时，要注意对公比进行分类讨论．思维启迪　分组求和即将不能直接求和的数列分解成若干个可以求和的数列，分别求和．求S＝12－22＋32－42＋…＋(－1)n－1n2(n∈N*)．错位相减法错位相减法主要适用于{an·bn}，其中{an}是等差数列，{bn}是等比数列．【点拨】　错位相减法的目的是构造特殊数列，即构造出等比数列，使之利用等比数列求和公式来求和．规律总结,运用公式求和要注意公式成立的条件，运用错位相减法求和时，相减后，若两边需除以含参数的代数式，则要讨论代数式是否为0的情况．对既不是等差数列也不是等比数列的数列，应先分析它的通项公式，抓住特点，将数列求和问题转化为已知的等差数列、等比数列的求和问题来解决．(2009·南通模拟)已知数列{an}的首项a1＝1，a2＝3，前n项和为Sn，且Sn＋1、Sn、Sn－1(n ≥2)分别是直线l上的点A、B、C的横坐标，【点拨】　在复杂的递推关系中，题目的前面的问题往往是与后面有联系的，前面的问题一般为后面的求解提供桥梁．【误区警示】　本题第一小问思路比较清晰，但不少学生因计算能力差因此得分较少，而第二小问出现了对数式，以及有关指数运算，再加上裂项又有难度，因此本题几乎没有得到多少分．【命题趋势】　高考中以考查等差、等比数列的求和公式为主，同时考查转化的思想，另外对非等差、等比数列求和，主要是考查学生的观察能力，分析问题与解决问题的能力及计算能力．数列求和题一直就是数列大题中的支柱内容．学而时习之，不亦说乎？第四节　数列的应用1.等差、等比数列的应用题常见于：产量增减、价格升降、细胞繁殖等问题，求利率、增长率等问题也常归结为数列建模问题．,2.将实际问题转化为数列问题时应注意：,(1)分清是等差数列还是等比数列；,(2)分清是求an还是求Sn，特别是准确地确定项数n.,3.将等比数列的通项公式和前n项求和公式应用到应用题的有关计算中去；增强应用意识，提高实际应用能力．4.解应用题的关键是建立数学模型，转化为数学问题，要加强培养学生的转化意识、加强方程思想的应用．1.夏季高山的温度从山脚起每升高100 m，降低0.7 ℃.已知某山山顶温度是14.8 ℃，山脚温度是26 ℃，则此山的相对高度是________m．【答案】　1 600【答案】　2703．已知{an}是递增的数列，且对于任意n∈N*，都有an＝n2＋λn成立，则实数λ的取值范围是________．【解析】　由题意知an＜an＋1恒成立，即2n＋1＋λ＞0恒成立，得λ＞－3.
【答案】　λ＞－34．现有200根相同的钢管，把它们堆放成正三角形垛，要使剩余的钢管尽可能的少，那么剩余钢管的根数为________．【答案】　105．用分期付款方式购买家用电器一件，价格为1 150元，购买当天先付150元，以后每月这一天都交付50元，并加付欠款利息，月利率为1%.若交付150元后的第一个月开始算分期付款的第一个月，全部欠款付清后，买这件家电实际付款________元．【答案】　1 2556．假设A型进口车关税税率在2003年是100%，在2008年是25%，在2003年A型进口车每辆价格为64万元(其中含32万元关税税款)
(1)已知与A型车性能相近的B型国产车，2003年每辆价格为46万元，若A型车的价格只受关税降低的影响，为了保证2008年B型车的价格不高于A型车价格的90%，B型车价格要逐年等额降低，问每年至少下降多少万元？
(2)某人在2003年将33万元存入银行，假设银行扣利息税后的年利率为1.8%(5年内不变)，且每年按复利计算(上一年的利息计入第二年的本金)，那么5年到期时这笔钱连本带利息是否一定够买按(1)中所述降价后的B型车一辆？(参考数据：1.0185≈1.093)【解】　(1)2008年A型车价格为32＋32×25%＝40(万元)
设B型车每年下降d万元，2003,2004，…，2008年B型车价格分别为a1，a2，a3…，a6(a1，a2，…，a6为公差是－d的等差数列)
∴a6≤40×90%，即46－5d≤36，∴d≥2，
故每年至少下降2万元．(2)2008年到期时共有钱33×(1＋1.8%)5≈33×1.093＝36.069>36(万元)
故5年到期后这笔钱够买一辆降价后的B型车．通项公式运用解数学问题应用题重点在过好三关：(1)事理关：阅读理解，知道命题所表达的内容；(2)文理关：将“问题情景”中的文字语言转化为符号语言，用数学关系式表述事件；(3)数理关：由题意建立相关的数学模型，将实际问题数学化，并解答这一数学模型，得出符合实际意义的解答．某地区发生流行性病毒感染，居住在该地区的居民必须服用一种药片预防，规定每人每天上午8时和晚上20时各服一片．现知该药片每片含药量为220毫克，若人的肾脏每12小时从体内滤出这种药的60%，该药物在人体内的残留量超过380毫克，就将产生副作用．
(1)某人上午8时第一次服药，问到第二天上午8时服完药后，这种药在他体内还残留多少？
(2)若人长期服用这种药，这种药会不会对人体产生副作用？说明理由．【点拨】　对数列应用题要分清是求通项问题还是求和问题．【解】　(1)设人第n次服药后，药在体内的残留量为an毫克，则
a1＝220，a2＝220＋a1×(1－60%)＝220×1.4＝308，
a3＝220＋a2×(1－60%)＝343.2，
即到第二天上午8时服完药后，这种药在他体内还残留343.2毫克；故若人长期服用这种药，这种药不会对人体产生副作用．求和公式运用数列应用题常见的模型有：一是等差模型，二是等比模型，在这两种模型中求和公式的运用是考查最多的．它与函数、方程、不等式等知识相互联系，无形中加大了综合力度．某市去年11月曾发生流感，据统计，11月1日该市新的流感病毒感染者有20人，此后，每天的新感染者平均比前一天的新感染者增加50人，由于该市医疗部门采取措施，使该种病毒的传播得到控制，从某天起，每天的新感染者平均比前一天的新感染者减少30人，到11月30日止，该市在这30天内感染该病毒的患者总共8 670人，问11月几日，该市感染此病毒的新患者人数最多？并求这一天的新患者人数．
【点拨】　本题关键在于抽象出等差数列的求和模型，然后利用方程思想进行求解．
【解】　设第n天新患者人数最多，则从n＋1天起该市医疗部门采取措施，前n天流感 病毒感染者总人数，构成一个首项为20，公差为50的等差数列的前n项和，单调性的应用数列是特殊的函数，因此解答时要注意函数性质的运用，如单调性、对称性等等．解答数列应用题的步骤为：审题；建模；求解；还原．其中在建模中，将已知条件翻译成数列语言，将实际问题转化为数学问题是非常关键的，要弄清该数列的特征和要求的问题．在一次人才招聘会上，有A、B两家公司分别开出它们的工资标准：A公司允诺第一年月工资为1 500元，以后每年月工资比上一年月工资增加230元；B公司允诺第一年月工资为2 000元，以后每年月工资在上一年的月工资基础上递增5%.设某人年初被A、B两家公司同时录取，试问：
(1)若该人分别在A公司或B公司连续工作n年，则他在第n年的月工资收入分别是多少？
(2)该人打算连续在一家公司工作10年，仅从工资收入总量较多作为应聘的标准(不计其他因素)，该人应该选择哪家公司，为什么？
(3)在A公司工作比在B公司工作的月工资收入最多可以多多少元？(精确到1元)并说明理由．【点拨】　本题涉及到两种数列，即等差数列与等比数列，“多收入”的问题可以理解成最值问题，借助数列单调性来解决．【解】　(1)此人在A、B公司第n年的月工资数分别为：
an＝1 500＋230×(n－1)(n∈N*)，
bn＝2 000(1＋5%)n－1(n∈N*)
(2)若该人在A公司连续工作10年，则工资收入总量为12(a1＋a2＋…＋a10)＝304 200(元)．
若该人在B公司连续工作10年，则工资收入总量为12(b1＋b2＋…＋b10)≈301 869(元)．
因为在A公司收入的总量高些，因此该人应该选择A公司．(3)问题等价于求Cn＝an－bn＝1 270＋230n－2 000×1.05n－1(n∈N*)的最大值．
当n≥2时，Cn－Cn－1＝230－100×1.05n－2
当Cn－Cn－1>0，即230－100×1.05n－2>0时，1．05n－2<2.3，得n<19.1
因此，当2≤n≤19时，
Cn－1∴C19＝a19－b19≈827(元)．
答：在A公司工作比在B公司工作的月工资收入最多可以多827元．假设某市2010年新建住房400万平方米，其中有250万平方米是中低价房，预计在今后的若干年内，该市每年新建住房面积平均比上一年增长8%.另外，每年新建住房中，中低价房的面积均比上一年增加50万平方米．那么，到哪一年底，(1)该市历年所建中低价房的累计面积(以2010年为累计的第一年)将首次不少于4 750万平方米？
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？(参考数据：1.084≈1.36,1.085≈1.47，1.086≈1.59)(2)设新建住房面积形成数列{bn}，由题意可知{bn}是等比数列，其中b1＝400，q＝1.08，则bn＝400·(1.08)n－1.由题意可知an＞0.85bn，即50n＋200＞400·(1.08)n－1·0.85.
当n＝5时，a5<0.85b5，当n＝6时，a6＞0.85b6，
∴满足上述不等式的最小正整数n为6.
∴到2015年底，当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.递推数列模型如果容易找到该数列任意一项an与它的前一或几项(或后一或几项)间的递推关系，那么我们可以用递推数列的知识求解．(本题满分14分)为了治理“沙尘暴”，西部某地区政府经过多年努力，到2009年底，将当地沙漠绿化了40%，从2010年开始，每年将出现这种现象：原有沙漠面积的12%被绿化，即改造为绿洲(被绿化的部分叫绿洲)，同时原有绿洲面积的8%又被侵蚀为沙漠，问至少经过几年的绿化，才能使该地区的绿洲面积超过50%？(可参考数据lg 2＝0.3，最后结果精确到整数)．【点拨】　本题要注意前后两年绿洲面积与沙漠面积的变化情况，特别是会根据绿洲面积的变化，列出递推关系式，求出通项公式，再结合不等式来求解．某国采用养老储备金制度．公民在就业的第一年就交纳养老储备金，数目为a1，以后每年交纳的数目均比上一年增加d(d＞0)，因此，历年所交纳的储备金数目a1，a2，…是一个公差为d的等差数列．与此同时，国家给予优惠的计息政策，不仅采用固定利率，而且计算复利．这就是说，如果固定年利率为r(r＞0)，那么在第n年末，第一年所交纳的储备金就变为a1(1＋r)n－1，第二年所交纳的储备金就变为a2(1＋r)n－2，…….以Tn表示到第n年末所累计的储备金总额．
(1)写出Tn与Tn－1(n≥2)的递推关系式；
(2)求证：Tn＝An＋Bn，其中{An}是一个等比数列，{Bn}是一个等差数列 规律总结数列应用题是高考命题的热点之一．解应用题的关键在于将实际问题抽象为数列模型．通过反复读题，列出有关信息，转化为数列的有关问题，这也是数学实际应用的具体体现(2009·湖南卷)将正△ABC分割成n2(n≥2，n∈N*)个全等的小正三角形(图2，图3分别给出了n＝2,3的情形)，在每个三角形的顶点各放置一个数，使位于△ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列，若顶点A ，B ，C处的三个数互不相同且和为1，记所有顶点上的数之和为f(n)，则有f(2)＝2，f(3)＝________，…，f(n)＝________.
图5－4－1【点拨】　本题可以先由几个特殊情况，列出f(2)＝2 ，f(3)＝，f(4)＝5……而后可采用不完全归纳法得出通项，但本题难度较大，理解起来比较困难．【解析】　当n＝3时，如图所示分别设各顶点的数用小写字母表示，即由条件知a＋b＋c＝1，x1＋x2＝a＋b，y1＋y2＝b＋c，z1＋z2＝c＋a
x1＋x2＋y1＋y2＋z1＋z2＝2(a＋b＋c)＝2,2g＝x1＋y2＝x2＋z1＝y1＋z2
6g＝x1＋x2＋y1＋y2＋z1＋z2＝2(a＋b＋c)＝2.【误区警示】　在最近几年高考试卷中，探索性题型在数列中考查较多，解决此类问题应具备较高的数学思维能力，研究与分析探索性题型有利于培养创新意识，但难度较大，不少学生找不到解题的思路，进入不了解题的切入点．
【命题趋势】　本节内容在高考中常常会以解答题形式出现，考查的力度非常大，从知识角度来说，数列是特殊的函数，对于等差、等比数列的综合运用，要从“注重数学思想方法、强化运算能力、重点知识重点训练”的角度做好准备．学而时习之，不亦说乎？