山东省2010年夏季普通高中学生学业水平考试数学全真模拟(一)
文档属性
| 名称 | 山东省2010年夏季普通高中学生学业水平考试数学全真模拟(一) |  | |
| 格式 | rar | ||
| 文件大小 | 35.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-27 06:42:00 | ||
图片预览


文档简介
山东省2010年夏季普通高中学生学业水平考试
数学全真模拟(一)
第一卷(选择题 共45分)
一、选择题(15’×3=45’)
1、已知角的终边经过点(-3,4),则tanx等于
A B C D
2、已知lg2=a,lg3=b,则lg等于
A a-b B b-a C D
3、设集合M=,则下列关系成立的是
A 1∈M B 2∈M C (1,2)∈M D (2,1)∈M
4、直线x-y+3=0的倾斜角是
A 300 B 450 C 600 D 900
5、底面半径为2,高为4的圆柱,它的侧面积是
A 8π B 16π C 20π D 24π
6、若b<0A b2a+b
7、已知x∈(-,o),cosx=,则tanx等于
A B C D
8、已知数列的前n项和sn=,则a3等于
A B C D
9、在ΔABC中,sinAsinB-cosAcosB<0则这个三角形一定是
A 锐角三角形 B 钝角三角形 C 直角三角形 D 等腰三角形
10、若函数,则f(x)
A 在(-2,+),内单调递增 B 在(-2,+)内单调递减
C 在(2,+)内单调递增 D 在(2,+)内单调递减
11、在空间中,a、b、c是两两不重合的三条直线,α、β、γ是两两不重合的三个平面,下列命题正确的是
A 若两直线a、b分别与平面α平行, 则a∥b
B 若直线a与平面β内的一条直线b平行,则a∥β
C 若直线a与平面β内的两条直线b、c都垂直,则a⊥β
D 若平面β内的一条直线a垂直平面γ,则γ⊥β
12、不等式(x+1)(x+2)<0的解集是
A B
C D
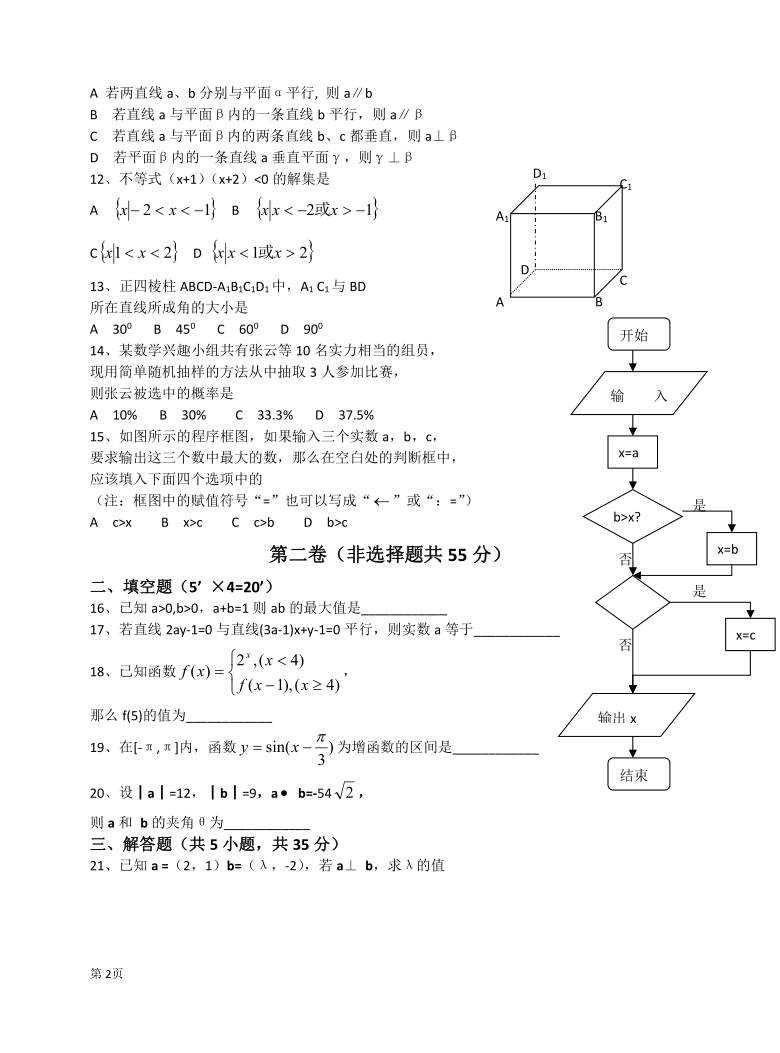
13、正四棱柱ABCD-A1B1C1D1中,A1 C1与BD
所在直线所成角的大小是
A 300 B 450 C 600 D 900
14、某数学兴趣小组共有张云等10名实力相当的组员,
现用简单随机抽样的方法从中抽取3人参加比赛,
则张云被选中的概率是
A 10% B 30% C 33.3% D 37.5%
15、如图所示的程序框图,如果输入三个实数a,b,c,
要求输出这三个数中最大的数,那么在空白处的判断框中,
应该填入下面四个选项中的
(注:框图中的赋值符号“=”也可以写成“”或“:=”)
A c>x B x>c C c>b D b>c
第二卷(非选择题共55分)
二、填空题(5’ ×4=20’)
16、已知a>0,b>0,a+b=1则ab的最大值是____________
17、若直线2ay-1=0与直线(3a-1)x+y-1=0平行,则实数a等于____________
18、已知函数,
那么f(5)的值为____________
19、在[-π,π]内,函数为增函数的区间是____________
20、设┃a┃=12,┃b┃=9,a b=-54,
则a和 b的夹角θ为____________
三、解答题(共5小题,共35分)
21、已知a =(2,1)b=(λ,-2),若a⊥ b,求λ的值
22、(6’)已知一个圆的圆心坐标为(-1, 2),且过点P(2,-2),求这个圆的标准方程
23、(7’)已知是各项为正数的等比数列,且a1=1,a2+a3=6,求该数列前10项的和Sn
24、(8’)已知函数
求f(x)的最大值,并求使f(x)取得最大值时x 的集合
25、(8’)已知函数f(x)满足xf(x)=b+cf(x),b≠0,f(2)=-1,且f(1-x)=-f(x+1)对两边都有意义的任意 x都成立
(1)求f(x)的解析式及定义域
(2)写出f(x)的单调区间,并用定义证明在各单调区间上是增函数还是减函数?
山东省2010年夏季普通高中学生学业水平考试
数学全真模拟(一)参考答案
选择题
DBCBB,DBABD,DADBA
二、填空题
16、 17、 18、8 19、 [,] 20、
三、解答题
21、解:∵a⊥b,∴ab=0,又∵a=(2,1),b =(λ,-2),∴ab=2λ-2=0,∴λ=1
22、解:依题意可设所求圆的方程为(x+1)2+(y-2)2=r2。
∵点P(2,-2)在圆上,
∴ r2=(2+1)2+(-2-2)2=25
∴所求的圆的标准方程是(x+1)2+(y-2)2=52 。
23、解:设数列的公比为q,由a1=1,a2+a3=6得:
q+q2=6,即q2+q-6=0,
解得q=-3(舍去)或q=2
∴S10=
24解:∵
∴f(x)取到最大值为1
当,f(x)取到最大值为1
∴f(x)取到最大值时的x的集合为
25、解:(1)由xf(x)=b+cf(x),b≠0,
∴x≠c,得,
由f(1-x)=-f(x+1)得
∴c=1
由f(2)=-1,得-1= ,即b=-1
∴,
∵1-x≠0,∴x≠1
即f(x)的定义域为
(2)f(x)的单调区间为(-,1),(1,+)且都为增区间
证明:当x∈(-,1)时,设x1则1- x1>0,1- x2>0
∴,
∵1- x1>0,1- x2>0
∴<0
即∴f(x)在(-,1)上单调递增。同理f(x)在(1,+)上单调递增。
数学全真模拟(一)
第一卷(选择题 共45分)
一、选择题(15’×3=45’)
1、已知角的终边经过点(-3,4),则tanx等于
A B C D
2、已知lg2=a,lg3=b,则lg等于
A a-b B b-a C D
3、设集合M=,则下列关系成立的是
A 1∈M B 2∈M C (1,2)∈M D (2,1)∈M
4、直线x-y+3=0的倾斜角是
A 300 B 450 C 600 D 900
5、底面半径为2,高为4的圆柱,它的侧面积是
A 8π B 16π C 20π D 24π
6、若b<0
7、已知x∈(-,o),cosx=,则tanx等于
A B C D
8、已知数列的前n项和sn=,则a3等于
A B C D
9、在ΔABC中,sinAsinB-cosAcosB<0则这个三角形一定是
A 锐角三角形 B 钝角三角形 C 直角三角形 D 等腰三角形
10、若函数,则f(x)
A 在(-2,+),内单调递增 B 在(-2,+)内单调递减
C 在(2,+)内单调递增 D 在(2,+)内单调递减
11、在空间中,a、b、c是两两不重合的三条直线,α、β、γ是两两不重合的三个平面,下列命题正确的是
A 若两直线a、b分别与平面α平行, 则a∥b
B 若直线a与平面β内的一条直线b平行,则a∥β
C 若直线a与平面β内的两条直线b、c都垂直,则a⊥β
D 若平面β内的一条直线a垂直平面γ,则γ⊥β
12、不等式(x+1)(x+2)<0的解集是
A B
C D
13、正四棱柱ABCD-A1B1C1D1中,A1 C1与BD
所在直线所成角的大小是
A 300 B 450 C 600 D 900
14、某数学兴趣小组共有张云等10名实力相当的组员,
现用简单随机抽样的方法从中抽取3人参加比赛,
则张云被选中的概率是
A 10% B 30% C 33.3% D 37.5%
15、如图所示的程序框图,如果输入三个实数a,b,c,
要求输出这三个数中最大的数,那么在空白处的判断框中,
应该填入下面四个选项中的
(注:框图中的赋值符号“=”也可以写成“”或“:=”)
A c>x B x>c C c>b D b>c
第二卷(非选择题共55分)
二、填空题(5’ ×4=20’)
16、已知a>0,b>0,a+b=1则ab的最大值是____________
17、若直线2ay-1=0与直线(3a-1)x+y-1=0平行,则实数a等于____________
18、已知函数,
那么f(5)的值为____________
19、在[-π,π]内,函数为增函数的区间是____________
20、设┃a┃=12,┃b┃=9,a b=-54,
则a和 b的夹角θ为____________
三、解答题(共5小题,共35分)
21、已知a =(2,1)b=(λ,-2),若a⊥ b,求λ的值
22、(6’)已知一个圆的圆心坐标为(-1, 2),且过点P(2,-2),求这个圆的标准方程
23、(7’)已知是各项为正数的等比数列,且a1=1,a2+a3=6,求该数列前10项的和Sn
24、(8’)已知函数
求f(x)的最大值,并求使f(x)取得最大值时x 的集合
25、(8’)已知函数f(x)满足xf(x)=b+cf(x),b≠0,f(2)=-1,且f(1-x)=-f(x+1)对两边都有意义的任意 x都成立
(1)求f(x)的解析式及定义域
(2)写出f(x)的单调区间,并用定义证明在各单调区间上是增函数还是减函数?
山东省2010年夏季普通高中学生学业水平考试
数学全真模拟(一)参考答案
选择题
DBCBB,DBABD,DADBA
二、填空题
16、 17、 18、8 19、 [,] 20、
三、解答题
21、解:∵a⊥b,∴ab=0,又∵a=(2,1),b =(λ,-2),∴ab=2λ-2=0,∴λ=1
22、解:依题意可设所求圆的方程为(x+1)2+(y-2)2=r2。
∵点P(2,-2)在圆上,
∴ r2=(2+1)2+(-2-2)2=25
∴所求的圆的标准方程是(x+1)2+(y-2)2=52 。
23、解:设数列的公比为q,由a1=1,a2+a3=6得:
q+q2=6,即q2+q-6=0,
解得q=-3(舍去)或q=2
∴S10=
24解:∵
∴f(x)取到最大值为1
当,f(x)取到最大值为1
∴f(x)取到最大值时的x的集合为
25、解:(1)由xf(x)=b+cf(x),b≠0,
∴x≠c,得,
由f(1-x)=-f(x+1)得
∴c=1
由f(2)=-1,得-1= ,即b=-1
∴,
∵1-x≠0,∴x≠1
即f(x)的定义域为
(2)f(x)的单调区间为(-,1),(1,+)且都为增区间
证明:当x∈(-,1)时,设x1
∴,
∵1- x1>0,1- x2>0
∴<0
即∴f(x)在(-,1)上单调递增。同理f(x)在(1,+)上单调递增。
同课章节目录
