第9章 多边形
图片预览






文档简介
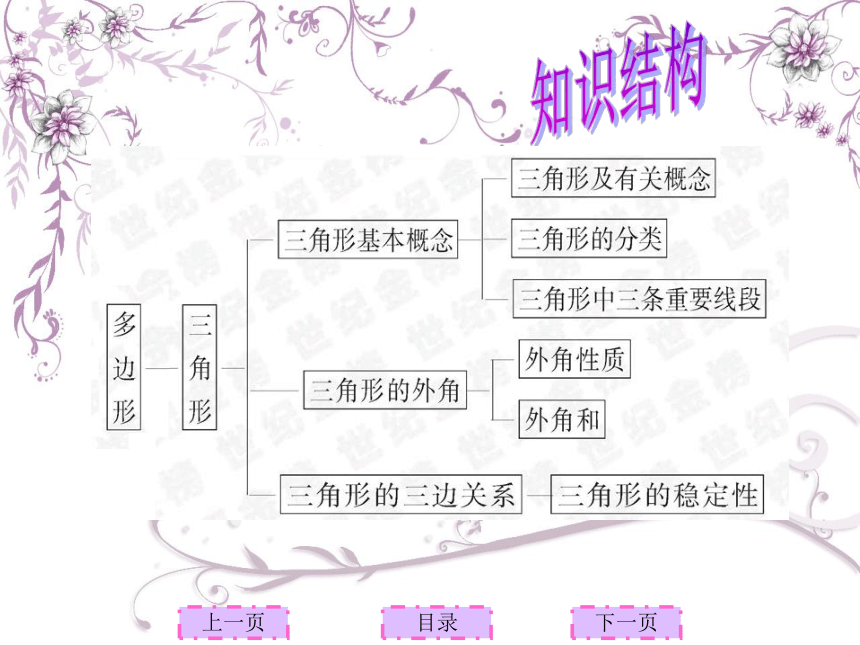
课件23张PPT。第九章多边形第十组制作9.19.29.3知识结构图多边形知识结构上一页下一页目录上一页下一页目录上一页下一页目录9.1三角形定义:1.三角形是由三条不在同一条直线上的线段首位顺次连结组成的平面图形,这三条线段就是三角形的边。
2.三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
3.三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。
4.三角形的三边关系:
(1)三角形任何两边的和大于第三边
(2)三角形任何两边的差小于第三边
5.三角形的外角和等于360°
6.三角形具有稳定性,四边形具有不稳定性
例题解析上一页下一页目录1.如图,AD=DE=BE,那么线段CD,CE
分别为△_______与△_______的中线.
【解析】∵AD=DE,
∴CD是△ACE的中线.
∵DE=BE,
∴CE是△DCB的中线.
ACE DCB上一页下一页目录2.如图所示,在△ABC中,∠ABC=90°,
AD是BC边上的中线,若△ABD的面积是
5 cm2,则△ABC的面积是_____cm2.
【解析】∵AD是BC边上的中线,
∴BC=2BD
∵S△ABD=5 cm2,
∴ BD·AB=5 cm2,
∴S△ABC= BC·AB= ·2BD·AB=BD·AB
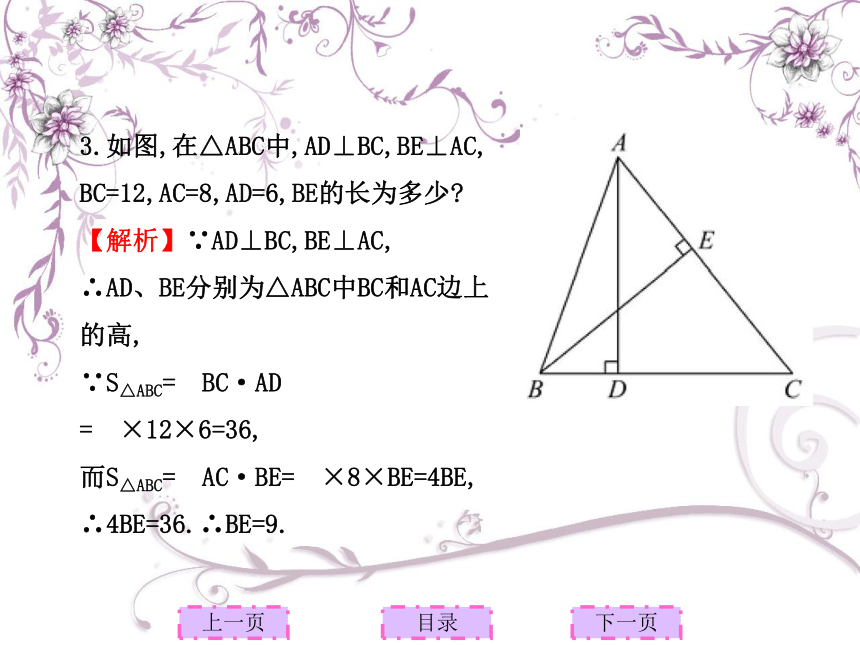
=10 (cm2).上一页下一页目录3.如图,在△ABC中,AD⊥BC,BE⊥AC,
BC=12,AC=8,AD=6,BE的长为多少?
【解析】∵AD⊥BC,BE⊥AC,
∴AD、BE分别为△ABC中BC和AC边上
的高,
∵S△ABC= BC·AD
= ×12×6=36,
而S△ABC= AC·BE= ×8×BE=4BE,
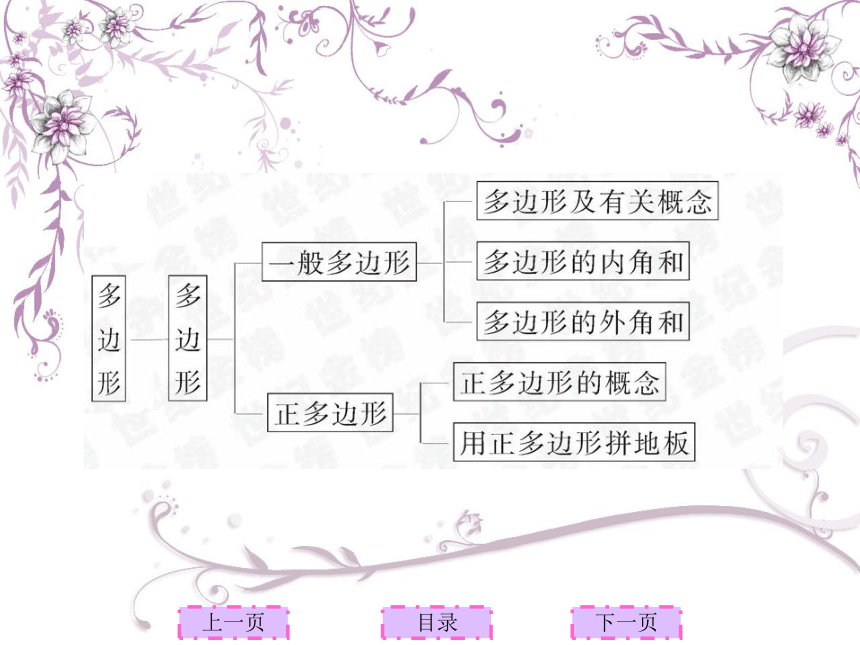
∴4BE=36.∴BE=9.9.2多边形的内角和与外角和定义:1.由n条不在同一直线上的线段首位顺次连结组成的平面图形成为n边形,又称为多边形。
2.如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。
3.连结多边形不相邻的两个顶角的线段叫做多边形的对角线。
4.N边形的内角和为:180°×(n-2)
5.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。上一页下一页目录上一页下一页目录 分别求出下列多边形的外角和的度数.360° 360° 360° 360° 3×180°=540°(n-2)·180°…n·180°……4×180°=720°5×180°=900°180°360°540°360°360°360°360°上一页下一页目录结论:n边形的内角与外角的总和为n·180°;
n边形的内角和为(n-2)·180°;那么多边形的外角和为 n·180°-(n-2)·180°因此,任意多边形的外角和都为360°.注:多边形的外角和与边数无关. =n·180°-n·180°+360°=360°例题解析[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形. 上一页下一页目录 例2 一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
分析: 正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°.设一个外角为x°,则内角为(x+36)°因为多边形的内角与相邻的外角互补;所以 x+x+36=180解得 x=72360÷72=5答 这个多边形的五边形.上一页下一页目录1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°CC巩固练习:上一页下一页目录3.若一个凸多边形的内角和等于它的外角和,则它的边数是_______.
4.如果一个多边形的每一个外角都相等,并且它的内角和为2880°,那么它的内角为_______.
5.一个多边形的每个外角都是12°,则这个多边形是________边形.
6.正n边形的一个内角为120°,那么n为( )
A.5 B.6 C.7 D.84160°30B上一页下一页目录9.3用正多边形拼地板定义:1.使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角是,就可以拼成一个平面图形。
2.两钟正多边形拼地板的有:
(1)正三角形与正方形
(2)正三角形与正六边形
(3)正三角形与正十二边形
(4)正方形与正八边形
上一页下一页目录演示上一页下一页目录正方形的镶嵌正三角形的镶嵌正六边形正五边形的镶嵌上一页下一页目录正方形和正八边形上一页下一页目录正方形和正八边形上一页下一页目录正十二边形和正三角形组合上一页下一页目录正六边形、正方形和正三角形的组合上一页下一页目录正十二边形、正六边形和正方形的组合上一页下一页目录
2.三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
3.三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。
4.三角形的三边关系:
(1)三角形任何两边的和大于第三边
(2)三角形任何两边的差小于第三边
5.三角形的外角和等于360°
6.三角形具有稳定性,四边形具有不稳定性
例题解析上一页下一页目录1.如图,AD=DE=BE,那么线段CD,CE
分别为△_______与△_______的中线.
【解析】∵AD=DE,
∴CD是△ACE的中线.
∵DE=BE,
∴CE是△DCB的中线.
ACE DCB上一页下一页目录2.如图所示,在△ABC中,∠ABC=90°,
AD是BC边上的中线,若△ABD的面积是
5 cm2,则△ABC的面积是_____cm2.
【解析】∵AD是BC边上的中线,
∴BC=2BD
∵S△ABD=5 cm2,
∴ BD·AB=5 cm2,
∴S△ABC= BC·AB= ·2BD·AB=BD·AB
=10 (cm2).上一页下一页目录3.如图,在△ABC中,AD⊥BC,BE⊥AC,
BC=12,AC=8,AD=6,BE的长为多少?
【解析】∵AD⊥BC,BE⊥AC,
∴AD、BE分别为△ABC中BC和AC边上
的高,
∵S△ABC= BC·AD
= ×12×6=36,
而S△ABC= AC·BE= ×8×BE=4BE,
∴4BE=36.∴BE=9.9.2多边形的内角和与外角和定义:1.由n条不在同一直线上的线段首位顺次连结组成的平面图形成为n边形,又称为多边形。
2.如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。
3.连结多边形不相邻的两个顶角的线段叫做多边形的对角线。
4.N边形的内角和为:180°×(n-2)
5.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。上一页下一页目录上一页下一页目录 分别求出下列多边形的外角和的度数.360° 360° 360° 360° 3×180°=540°(n-2)·180°…n·180°……4×180°=720°5×180°=900°180°360°540°360°360°360°360°上一页下一页目录结论:n边形的内角与外角的总和为n·180°;
n边形的内角和为(n-2)·180°;那么多边形的外角和为 n·180°-(n-2)·180°因此,任意多边形的外角和都为360°.注:多边形的外角和与边数无关. =n·180°-n·180°+360°=360°例题解析[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形. 上一页下一页目录 例2 一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
分析: 正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°.设一个外角为x°,则内角为(x+36)°因为多边形的内角与相邻的外角互补;所以 x+x+36=180解得 x=72360÷72=5答 这个多边形的五边形.上一页下一页目录1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°CC巩固练习:上一页下一页目录3.若一个凸多边形的内角和等于它的外角和,则它的边数是_______.
4.如果一个多边形的每一个外角都相等,并且它的内角和为2880°,那么它的内角为_______.
5.一个多边形的每个外角都是12°,则这个多边形是________边形.
6.正n边形的一个内角为120°,那么n为( )
A.5 B.6 C.7 D.84160°30B上一页下一页目录9.3用正多边形拼地板定义:1.使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角是,就可以拼成一个平面图形。
2.两钟正多边形拼地板的有:
(1)正三角形与正方形
(2)正三角形与正六边形
(3)正三角形与正十二边形
(4)正方形与正八边形
上一页下一页目录演示上一页下一页目录正方形的镶嵌正三角形的镶嵌正六边形正五边形的镶嵌上一页下一页目录正方形和正八边形上一页下一页目录正方形和正八边形上一页下一页目录正十二边形和正三角形组合上一页下一页目录正六边形、正方形和正三角形的组合上一页下一页目录正十二边形、正六边形和正方形的组合上一页下一页目录
