6.3平面直角坐标系(2)
文档属性
| 名称 | 6.3平面直角坐标系(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 21.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-02 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
6.3
平面直角坐标系(2)
[学习目标]
1. 认识平面直角坐标系,了解点的坐标的意义,会用坐标表示点,能画出点的坐标位
2. 渗透对应关系,提高学生的数感.
[复习]
____________叫平面直角坐标系,________叫横轴(又叫X轴)_______叫纵轴(又叫Y轴),________原点
请写出图中A,B,C,DE,F,G,M的坐标
A( , ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , ) M( , )
板块一:认识象限
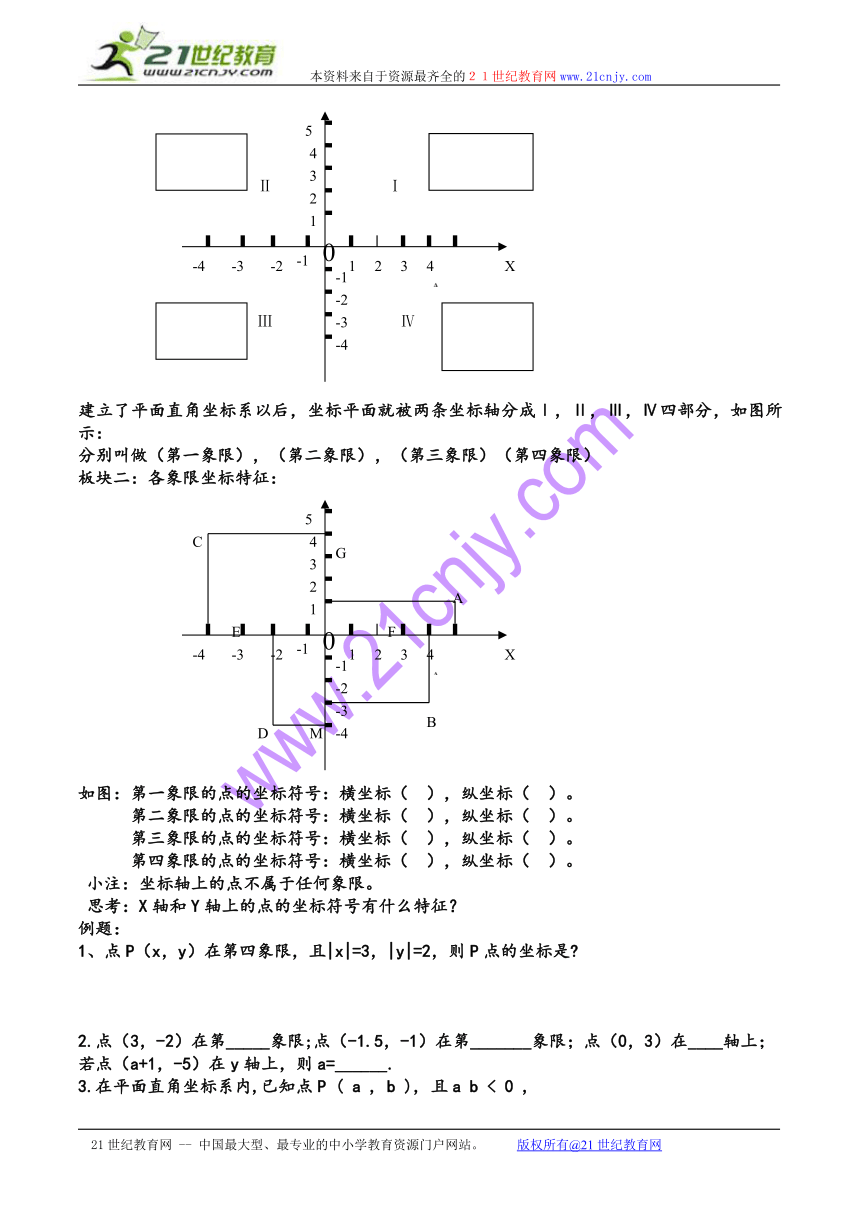
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四部分,如图所示:
分别叫做(第一象限),(第二象限),(第三象限)(第四象限)
板块二:各象限坐标特征:
如图:第一象限的点的坐标符号:横坐标( ),纵坐标( )。
第二象限的点的坐标符号:横坐标( ),纵坐标( )。
第三象限的点的坐标符号:横坐标( ),纵坐标( )。
第四象限的点的坐标符号:横坐标( ),纵坐标( )。
小注:坐标轴上的点不属于任何象限。
思考:X轴和Y轴上的点的坐标符号有什么特征?
例题:
1、点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是
2.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
3.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________
板块三 点到两轴的距离
小结:点M(a,b)到X轴的距离是( ),到Y轴的距离是
( )
例题:
1点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 。
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
.
练一练:
1点 M(- 8,12)到 x轴的距离是_________,到 y轴的距离是________.
2若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是________
3点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
4已知点M(a,b),当a>0,b>0时,M在第_______象限;当a____,b______时,M 在第二象限;当a_____,b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
选择题:
1.如图1所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( )
A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.若点M的坐标是(a,b),且a>0,b<0,
则点M在( )
A.第一象限;B.第二象限; C.第三象限;
D.第四象限
填空题:
1.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
2.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
3.在坐标平面内,已知点A(a,b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
A
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
B
C
D
X
G
E
F
M
y
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
Ⅲ
X
Ⅱ
Ⅰ
Ⅳ
A
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
B
C
D
X
G
E
F
M
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
X
M
M到X轴的距离是多少?
M到Y轴的距离是多少?
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
6.3
平面直角坐标系(2)
[学习目标]
1. 认识平面直角坐标系,了解点的坐标的意义,会用坐标表示点,能画出点的坐标位
2. 渗透对应关系,提高学生的数感.
[复习]
____________叫平面直角坐标系,________叫横轴(又叫X轴)_______叫纵轴(又叫Y轴),________原点
请写出图中A,B,C,DE,F,G,M的坐标
A( , ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , ) M( , )
板块一:认识象限
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四部分,如图所示:
分别叫做(第一象限),(第二象限),(第三象限)(第四象限)
板块二:各象限坐标特征:
如图:第一象限的点的坐标符号:横坐标( ),纵坐标( )。
第二象限的点的坐标符号:横坐标( ),纵坐标( )。
第三象限的点的坐标符号:横坐标( ),纵坐标( )。
第四象限的点的坐标符号:横坐标( ),纵坐标( )。
小注:坐标轴上的点不属于任何象限。
思考:X轴和Y轴上的点的坐标符号有什么特征?
例题:
1、点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是
2.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
3.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________
板块三 点到两轴的距离
小结:点M(a,b)到X轴的距离是( ),到Y轴的距离是
( )
例题:
1点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 。
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
.
练一练:
1点 M(- 8,12)到 x轴的距离是_________,到 y轴的距离是________.
2若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是________
3点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
4已知点M(a,b),当a>0,b>0时,M在第_______象限;当a____,b______时,M 在第二象限;当a_____,b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
选择题:
1.如图1所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( )
A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.若点M的坐标是(a,b),且a>0,b<0,
则点M在( )
A.第一象限;B.第二象限; C.第三象限;
D.第四象限
填空题:
1.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
2.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
3.在坐标平面内,已知点A(a,b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
A
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
B
C
D
X
G
E
F
M
y
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
Ⅲ
X
Ⅱ
Ⅰ
Ⅳ
A
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
B
C
D
X
G
E
F
M
1
2
3
4
-1
-2
-3
-4
1
2
-4
-2
-3
-1
0
3
5
4
X
M
M到X轴的距离是多少?
M到Y轴的距离是多少?
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
