§1.1 等腰三角形的性质与判定

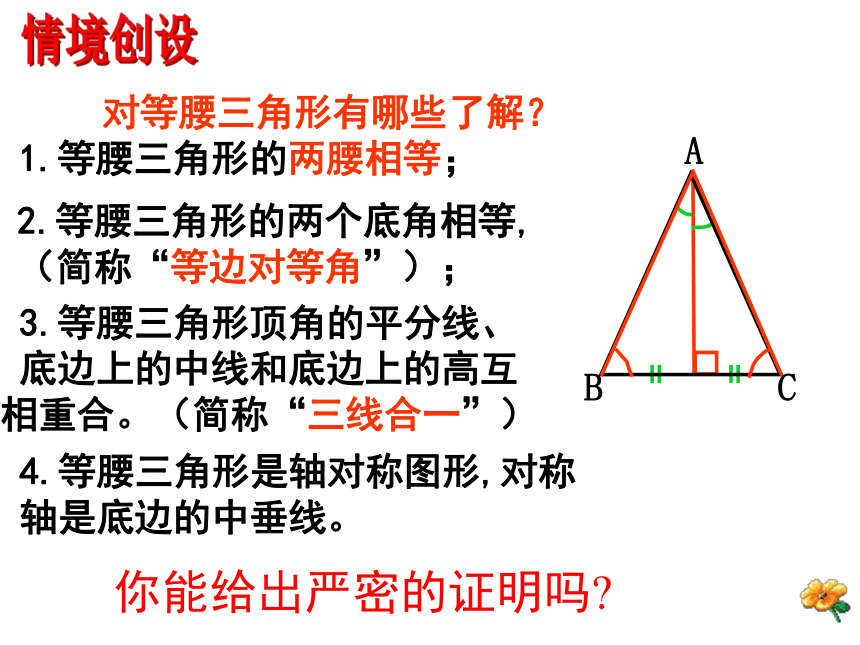
课件21张PPT。九年级数学（上册）第一章 证明(二)§1.1等腰三角形的性质与判定主备人:李志勇 复核人：程伟伟1.等腰三角形的两腰相等；2.等腰三角形的两个底角相等,（简称“等边对等角”）；3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。（简称“三线合一”）4.等腰三角形是轴对称图形,对称轴是底边的中垂线。你能给出严密的证明吗?情境创设求证：等腰三角形的两个底角相等（“等边对等角”）已知：如图，在△ABC中，AB=AC
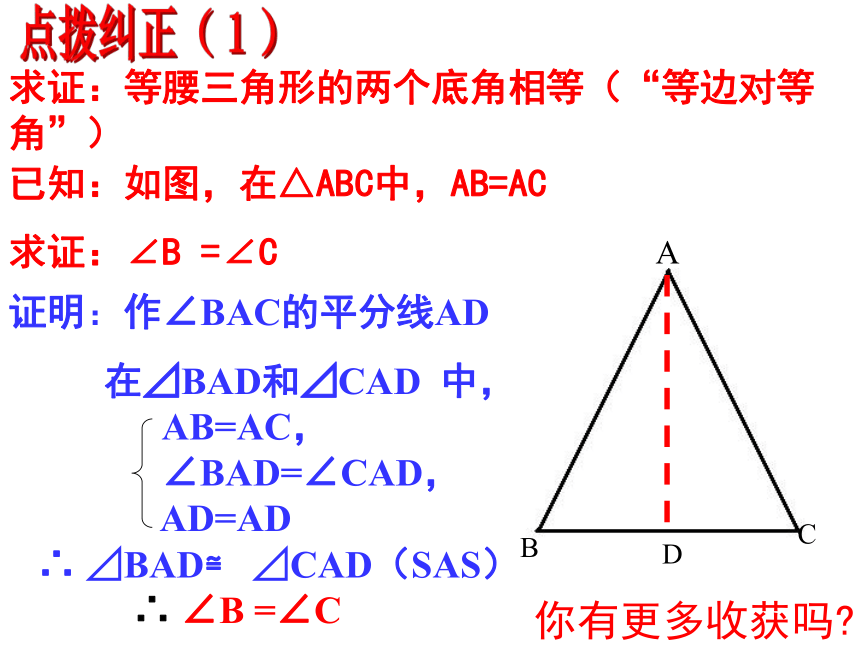
求证：∠B =∠CACBD证明：作∠BAC的平分线AD
在⊿BAD和⊿CAD 中，
AB=AC，
∠BAD=∠CAD，
AD=AD
∴ ⊿BAD≌ ⊿CAD（SAS）
∴ ∠B =∠C
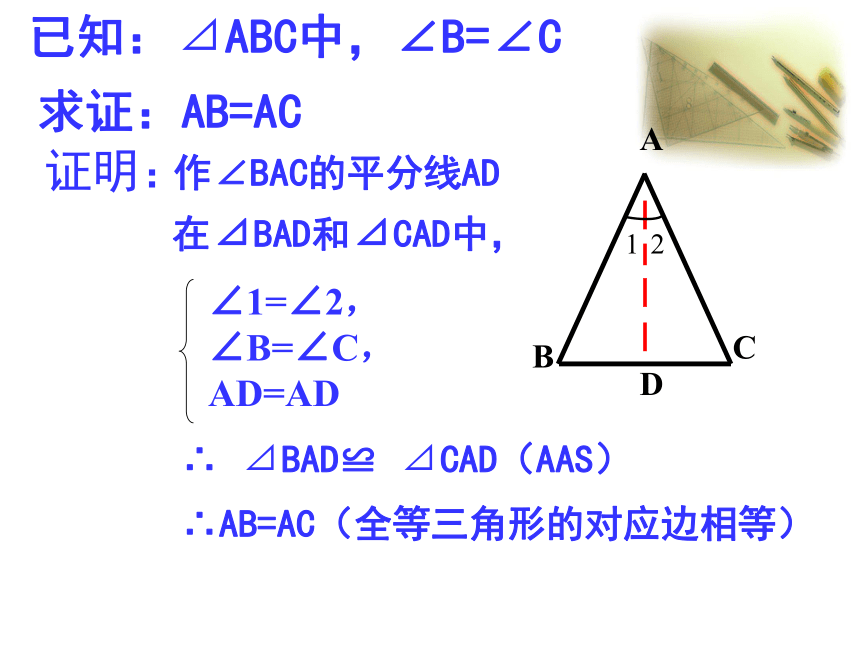
你有更多收获吗?点拨纠正（１）定理：等腰三角形的两个底角相等（“等边对等角”）你能用几种方法证明？情境创设定理２：等腰三角形的顶角平分线、底边上的中线和高是同一条线段。（三线合一）定理３：如果一个三角形的两个角相等，那么这个这两个角所对的边也相等（“等角对等边”）已知：⊿ABC中，∠B=∠C求证：AB=AC证明：作∠BAC的平分线AD在⊿BAD和⊿CAD中，∠1=∠2，
∠B=∠C，
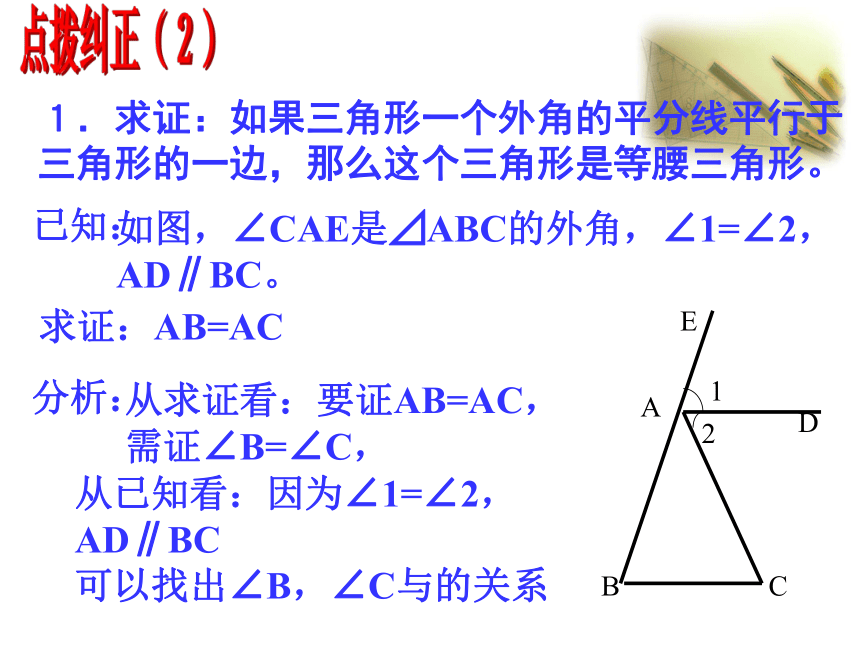
AD=AD∴ ⊿BAD≌ ⊿CAD（AAS）∴AB=AC（全等三角形的对应边相等）12１．求证：如果三角形一个外角的平分线平行于
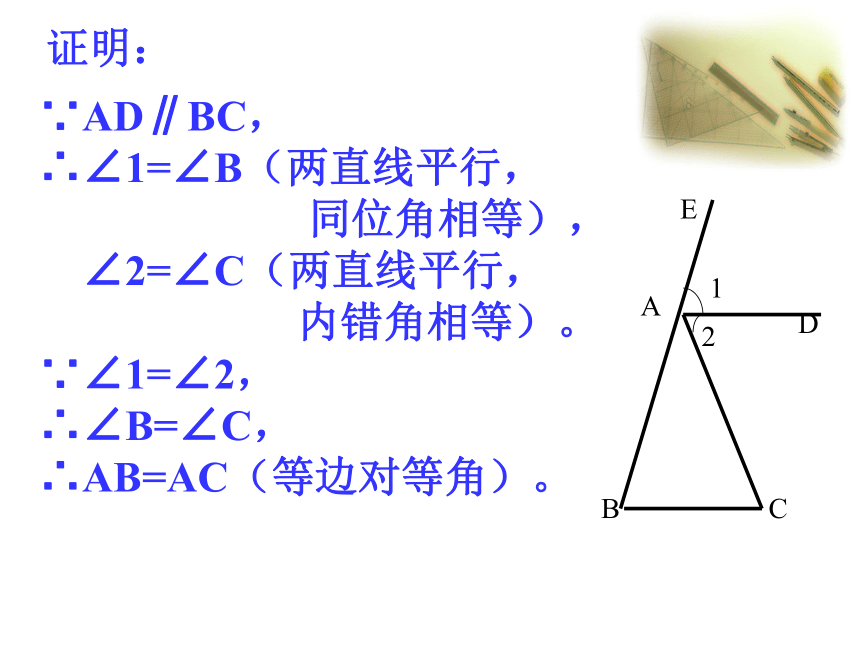
三角形的一边，那么这个三角形是等腰三角形。点拨纠正（２）证明：∵AD∥BC，
∴∠1=∠B（两直线平行，
同位角相等），
∠2=∠C（两直线平行，
内错角相等）。
∵∠1=∠2，
∴∠B=∠C，
∴AB=AC（等边对等角）。２．变式1：如图，∠EAC是△ABC的外角，AD平分∠EAC，且AB=AC
求证：AD∥BC.
ABCDE３．变式2：如果AB=AC，AD∥BC，
那么AD平分∠EAC吗？角平分线、平行线，等腰三角形这三个
结论中有两个成立，第三个一定成立。(1)如果等腰三角形的一个底角为500，则其余两个角为____和____.(2)如果等腰三角形的顶角为800，则它的一个底角为____.5008005001.填空题(3)如果等腰三角形的一个角为800，则其余两个角为___________________.800和200(4)如果等腰三角形的一个角为1000，则其余两个角为_________.400和400或500和500才艺展示(4)钝角三角形不可能是等腰三角形 . （ ）2. 判断下列语句是否正确.(1)等腰三角形的角平分线、中线和高互相重合.( )××(5)等腰三角形的一个外角为1300，则三个内角分别:_______________________________.650、650、500或500、500、800(3)等腰三角形的底角都是锐角. （ ） (2)有一个角是60°的等腰三角形，其它两个内角也为60°. （ ） ３．已知：如图（１），∠A =360 , ∠DBC =360 ， 　　　　∠C=720．计算∠1和∠2，并说明图中有哪些等腰三角　　　形？才艺展示４.已知：如图（２），CD是等腰直角三角形ABC斜边上的高，找出图中有哪些等腰直角三角形。５.已知：如图（３），AD ∥BC，BD平分∠ABC。
求证：AB=AD图（１）图（２）图（３）1、证明：两角及其中一角的对边对应相等的两个三角形全等。 7.(只画图,写出已知和求证,不证明)2、证明：等边三角形的每个角都相等.
3、证明：线段垂直平分线上的 点到线段两端距离相等。　1.如图，AD是△ABC的角平分线AB=AC+DC，求证：∠C=2∠BABCDE3.如图，AB＞AC，AD是角平分线，E是AB上的一点，AE=AC，EF∥BC交AC于F，求证：CE平分∠DEF有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.1.等角对等边,1.两腰相等.