§1.2 直角三角形全等的判定（1）

课件17张PPT。九年级数学（上册）第一章 证明(二)§1.2(1)直角三角形全等的判定主备人：李志勇 复核人：程伟伟 １．三角形全等的判定定理有哪些?
２．两边及其中一边的对角对应相等　　　　　　　　　　　　　　　　　　 的两个三角形全等吗?
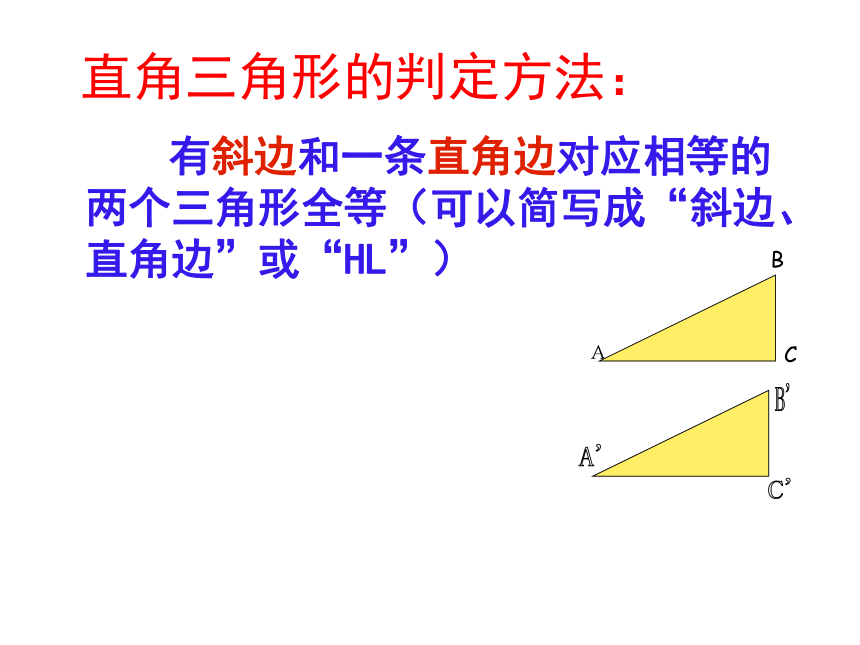
　３．如果其中一边所对的角是直角呢情景创设请提出你的猜想.直角三角形的判定方法：　　　有斜边和一条直角边对应相等的两个三角形全等（可以简写成“斜边、直角边”或“HL”）
B'ＡC'A'CB如图在Δ ABC和Δ A’B’C’中， ∠ C= ∠ C’=RT∠, AB=A’B’，AC=A’C’
求证:Δ ABC≌Δ A’B’C’ 。
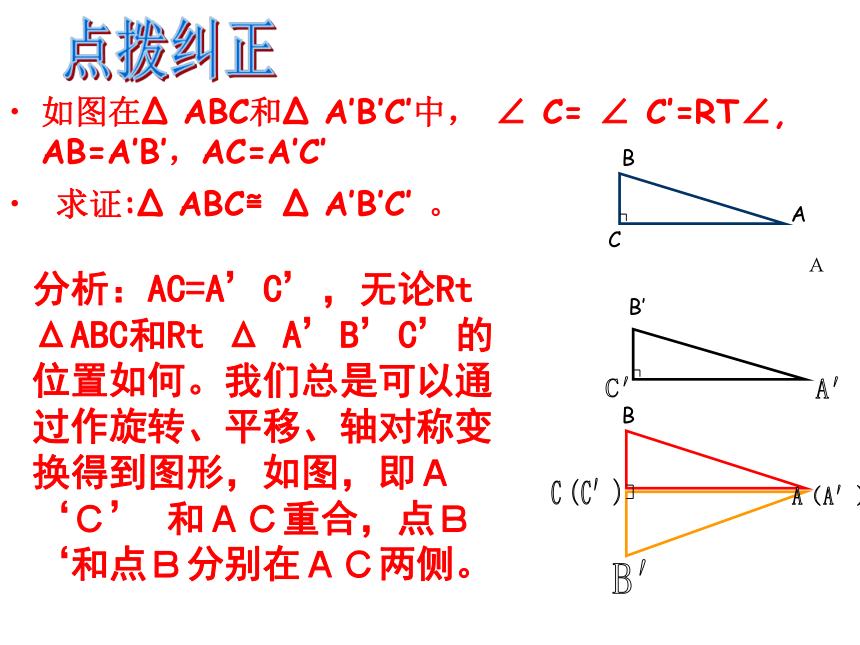
C（C′）A（A′）B′A′C′Ａ分析：AC=A’C’，无论Rt ΔABC和Rt Δ A’B’C’的位置如何。我们总是可以通过作旋转、平移、轴对称变换得到图形，如图，即Ａ‘Ｃ’ 和ＡＣ重合，点Ｂ‘和点Ｂ分别在ＡＣ两侧。BBCAB′点拨纠正如图:在Δ ABC和Δ A’B’C’中，
∠ C= ∠ C’=RT∠, AB=A’B’，AC=A’C’
求证:Δ ABC≌Δ A’B’C’ 。
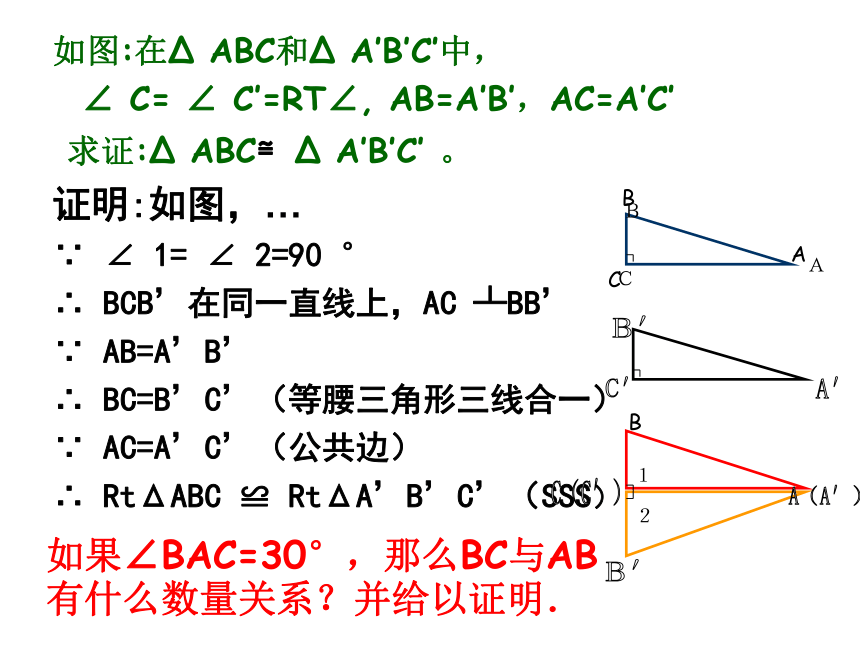
证明:如图，…
∵ ∠ 1= ∠ 2=90 °
∴ BCB’在同一直线上，AC ┴BB’
∵ AB=A’B’
∴ BC=B’C’（等腰三角形三线合一）
∵ AC=A’C’（公共边）
∴ RtΔABC ≌ RtΔA’B’C’（SSS）C（C′）A（A′）B′B′A′C′ＡＣＢ１２BCAB如果∠BAC=30°，那么BC与AB有什么数量关系？并给以证明．直角三角形的判定方法：　　　有斜边和一条直角边对应相等的两个三角形全等（可以简写成“斜边、直角边”或“HL”）
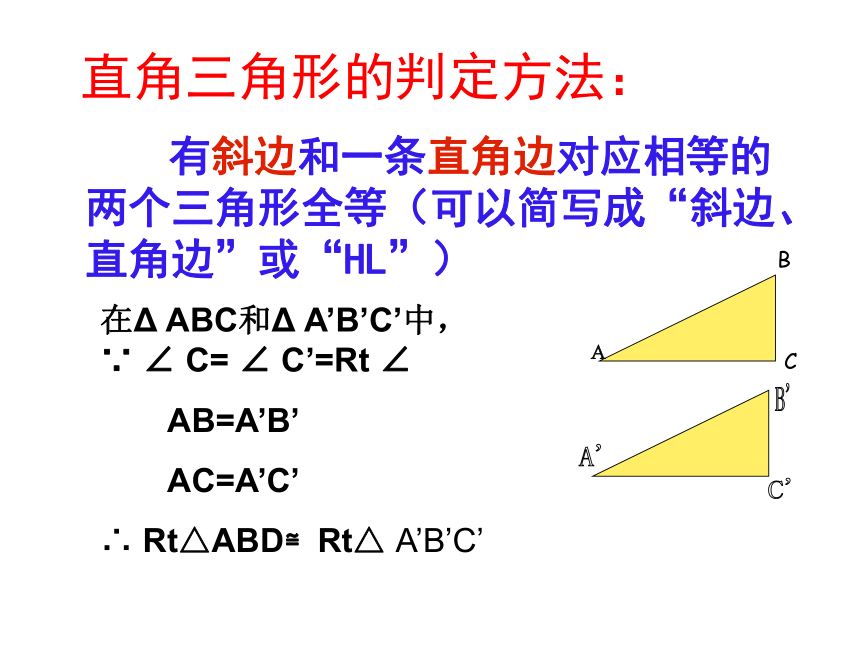
B'ＡC'A'在Δ ABC和Δ A’B’C’中， ∵ ∠ C= ∠ C’=Rt ∠
　　AB=A’B’
　　AC=A’C’
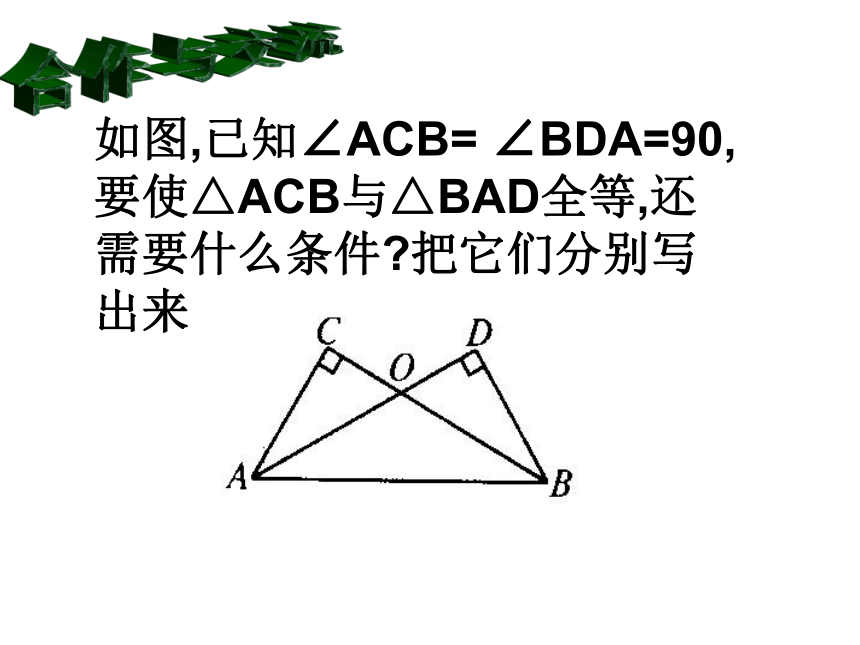
∴ Rt△ABD≌Rt△ A’B’C’ CB如图,已知∠ACB= ∠BDA=90,要使△ACB与△BAD全等,还需要什么条件?把它们分别写出来.合作与交流1.下列判断对吗?并说明理由:1)两个锐角对应相等的两个直角三角形全等;2)斜边及一个锐角对应相等的两个直角三角形全等;3)两直角边对应相等的两个直角三角形全等;4)一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.才艺展示 2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,
垂足分别为E,F,DE=BF.
求证: (1)AE=CF;
(2)AB∥CD.才艺展示3.如图:CD⊥AB,BE⊥AC,垂足分别
为D、E，BE、CD相交于点O。如
果AB=AC，那么图中有几对全等的
直角三角形？试证明你的结论。 ４. 如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。解：BD=CD
∵∠ADB=∠ADC=90°
AB=AC
AD=AD∴Rt△ABD≌Rt△ACD(HL)
∴BD=CD５.已知:如图,D是△ABC的BC边上
的中点,DE⊥AC,DF⊥AB,
垂足分别为E、F，
且DE =DF。
求证: △ABC是
等腰三角形.
１．用三角尺作角平分线再过点M作OA的垂线,如图:在已知∠AOB的两边OA,OB上
分别取点M,N,使OM=ON;过点N作OB的垂线,两垂线交于点P,那么射线OP就是∠AOB的平分线.请你证明OP平分∠AOB.P已知:如图,OM=ON,PM⊥OM,PN⊥ON,PM与PN交于点P.
求证:∠AOP=∠BOP.先把它转化为一个纯数学问题:●拓展与延伸 ２.如图，在△ABC与△A′B′C中， CD， C′D′分别是高，并且AC＝A′C′，CD＝C′D′，∠ACB＝∠A′C′B′．
求证：△ABC≌△A′B′C′．拓展与延伸小 结 你能够用几种方法说明两个直角三角形全等？ 直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS，还有直角三角形特殊的判定方法——“HL”.定理：等腰三角形的两个底角相等（“等边对等角”）定理：等腰三角形的顶角平分线、底边上的中线和高是同一条线段（三线合一）定理：如果一个三角形的两个角相等，那么这个这两个角所对的边也相等（“等角对等边”）定理回顾定理：两角及其中一角的对边对应相等的两个三角形全等。定理：等边三角形的每个角都相等. 定理：线段垂直平分线上的 点到线段两端距离相等。定理：3个角都相等的三角形是等边三角形. 定理：到一条线段两端距离相等的点在这条线段垂直平分线上。