函数的单调性

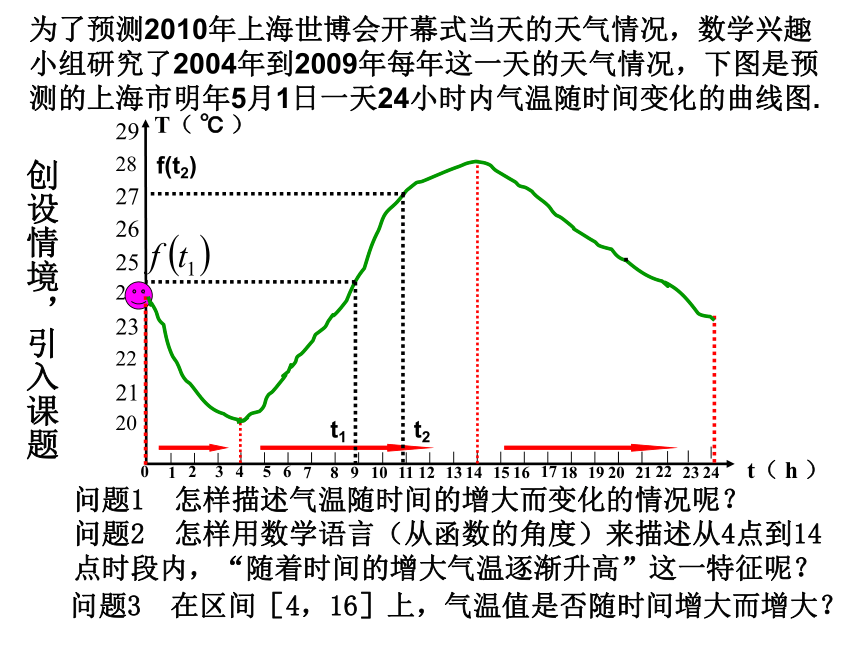
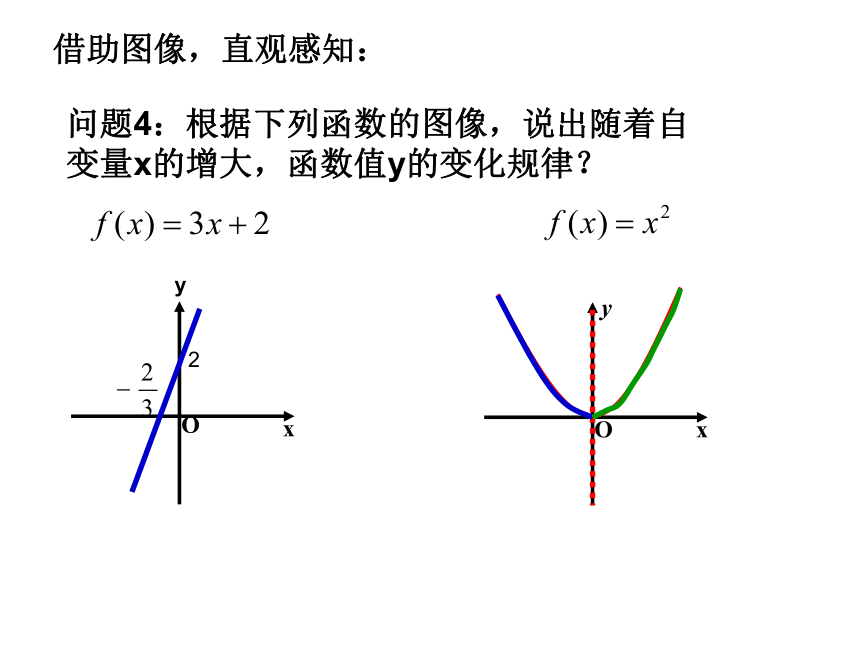
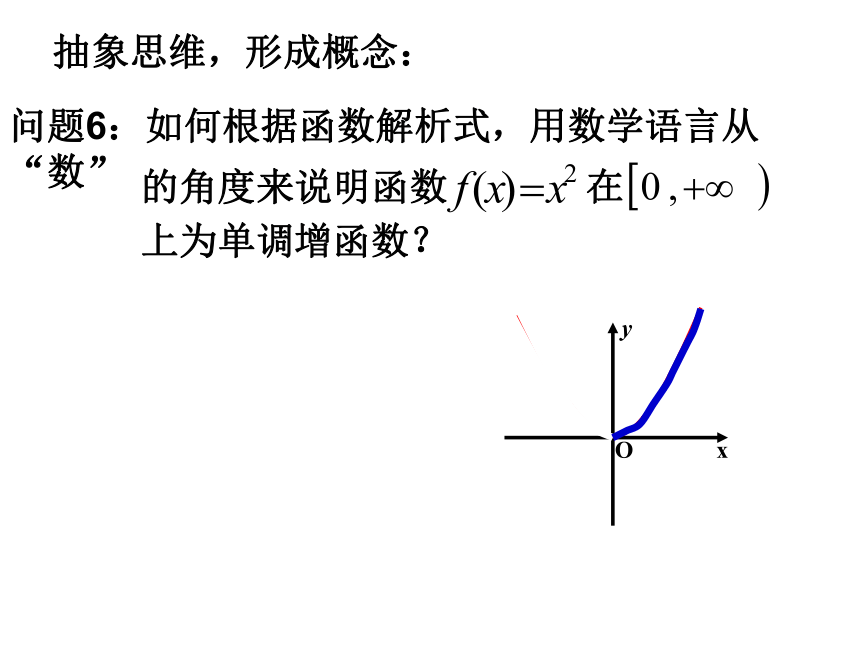
课件18张PPT。为了预测2010年上海世博会开幕式当天的天气情况，数学兴趣小组研究了2004年到2009年每年这一天的天气情况，下图是预测的上海市明年5月1日一天24小时内气温随时间变化的曲线图.t（ h ）问题1 怎样描述气温随时间的增大而变化的情况呢？问题2 怎样用数学语言（从函数的角度）来描述从4点到14点时段内，“随着时间的增大气温逐渐升高”这一特征呢？问题3 在区间［4，16］上，气温值是否随时间增大而增大？创设情境，引入课题 函数的单调性大新中学 赵晓凤借助图像，直观感知： 问题4：根据下列函数的图像，说出随着自变量x的增大，函数值y的变化规律？问题5：能否根据自己的理解，说说什么是单调增函数，单调减函数呢？如果函数在某个区间上随自变量x的增大，函数值y越来越大，我们说函数在该区间上为单调增函数；如果函数在某个区间上随自变量x的增大，函数值y越来越小，我们说函数在该区间上为单调减函数。借助图像，直观感知： 抽象思维，形成概念： 问题7：如何用准确的数学语言表述出单调增函数的定义呢?请类比描述单调减函数的定义抽象思维，形成概念： 1、单调增函数 如果对于区间I内的任意两个实数x1、x2，当x1＜x2时，都
有f(x1)＜f(x2)，那么就说y＝f(x)在区间I上是单调增函数， I称为y＝f(x)的单调增区间．一般地，设函数y ＝ f(x) 的定义域为D，区间I D．2、单调减函数一般地，设函数y ＝ f(x) 的定义域为D，区间I D． 如果对于区间I内的任意两个实数x1、x2，当x1＜x2时，都
有f(x1)>f(x2)，那么就说y＝f(x)在区间I上是单调减函数， I称为y＝f(x)的单调减区间．如果函数y＝f(x)在区间I上是单调增函数或单调减函数，那么就说函数y＝f(x) 在区间I上具有单调性，函数y＝f(x)称为区间I上的单调函数；单调增区间和单调减区间统称为单调区间。 3、单调性、单调区间抽象思维，形成概念： 单调增区间：单调减区间： [4，14][0，4]，[14，24]口答：你能找出气温图中的单调区间吗?巩固概念，应用提高: 判断： 2、定义在R上的函数f(x)满足f(-1)巩固概念，应用提高: 巩固概念，应用提高: 例1、运用函数单调性的定义证明：函数 在区间 上是增函数。问题8：你能归纳运用定义法探求并证明函数单调性的步骤吗？（1）取值（2）作差（3）变形（4）定号（5）下结论例2、运用函数单调性的定义证明：函数 在 上的单调性。巩固概念，应用提高: 问题9：函数 在定义域R上是单调函数吗？能用我们今天学习的函数单调性定义说说为什么吗？巩固概念，应用提高: 问题10：能说说函数 的单调性情况吗?巩固概念，应用提高: 问题11：如何说明一个函数在某个区间上是单调函数？又如何说明一个函数在某个区间上不是单调函数呢？ 巩固概念，应用提高: 若函数在某个区间上不是单调函数，举反例即可。课堂小结：请谈谈本节课的收获与体会！课后探究：1、讨论函数 （x>0）的单调性 2、判断函数 在[- 2, 3]上的单调性，并指出它的单调区间. 3、二次函数 在［0，＋∞）是增函数，你能确定字母的值吗？ 谢谢！