函数的单调性
图片预览


文档简介
函数的单调性
崇明县大新中学 赵晓凤
一、教学内容分析:
《函数单调性》是高级中学数学学科,上海教育出版社出版的高一年级(第一学期)第三章《函数》,第四单元《函数性质》的第二节,该课时主要学习增函数、减函数的定义,以及应用定义解决一些简单问题。
二、教材所处地位和作用:
函数的单调性是函数众多性质中的重要性质之一,在解决函数值域、定义域、不等式、比较两数大小等具体问题中均需用到函数的单调性;在本节课的教学中以函数的单调性的概念为线,它始终贯穿于整个课堂教学过程;利用函数的单调性的定义证明具体函数的单调性是对函数单调性概念的深层理解,且“作差、变形、判号、定论”的过程学生不易掌握。
学生只学过一次函数、反比例函数、正比例函数、二次函数,所以对函数的单调性研究也只能限于这几种函数,学生的现有认知结构中,能根据函数的图像观察出“随着自变量的增大函数值增大”等变化趋势,所以在教学中要充分利用好函数图像的直观性,发挥好多媒体教学的优势;同时在这一节中利用函数图像来研究函数性质的数形结合思想,将贯穿于我们整个高中数学教学。
三、教学目标的确定:
依据二期课改的理念及高中数学课程标准的要求,并结合学生的认知规律和实际特点,确定本节课教学目标如下:
知识与技能:从形与数两方面理解函数单调性的概念,初步掌握利用函数图像和定义判断、证明函数单调性的方法.
过程能力与方法:通过对函数单调性定义的探究,渗透数形结合的思想方法,培养观察、归纳、抽象的能力和语言表达能力,通过对函数单调性的证明,提高推理论证的能力。
情感态度价值观:通过知识的探究过程,培养细心观察、认真分析、严谨论证的良好思维习惯,感知从具体到抽象,从感性到理性的认知过程。
【教学重点】 函数单调性的概念的理解、判断及证明。
【教学难点】 根据定义证明函数的单调性。
由于本节内容涉及的问题都要通过函数增减性的定义来解决,因此确定本节课教学重点为函数单调性概念的理解、判断及证明,使用定义去证明函数单调性需灵活运用,故确定为本节的教学难点。
四、教法与学法:
1、教法分析:
依据目前教育发展和二期课改的精神及当前积极倡导“培养学生的探究精神和实践能力”的迫切需要。结合学生的认知水平,寓教学于情境之中,体现数学与现实生活的联系。采用“以学生为主体,以问题为中心”的问题驱动式教学模式,意在调动学生的积极性,让学生主动参与到教学活动中。为了突出重点,突破难点,在教学中采取以下措施:
从学生已有的生活经验,知识背景,精心设计一些适合学生学力的具体问题情境,逐步引导学生发现与探索,归纳出增、减函数的概念。
另外在教学过程中,从实际问题入手,利用学生的生活经验和感性认知,借助电教手段,生动直观地分析问题,从而增强学习的可接受性,同时诱导和启发学生主动学习,探究学习。
2、学法指导:
在本节课的教学中,教会学生善于观察,认真分析,最后从直观中抽象出理论和知识,使获取知识和培养能力融为一体,使学生主体地位得以实现,真正实现本节课的教学目标。
3、教学手段:
为了更形象、直观地突出重点,突破难点,增大教学容量,提高教学效率,本节课采用多媒体辅助教学。
五、教学方法:教师启发讲授,学生探究学习.
六、教学过程:
教学环节 教 学 过 程 设 计 意 图
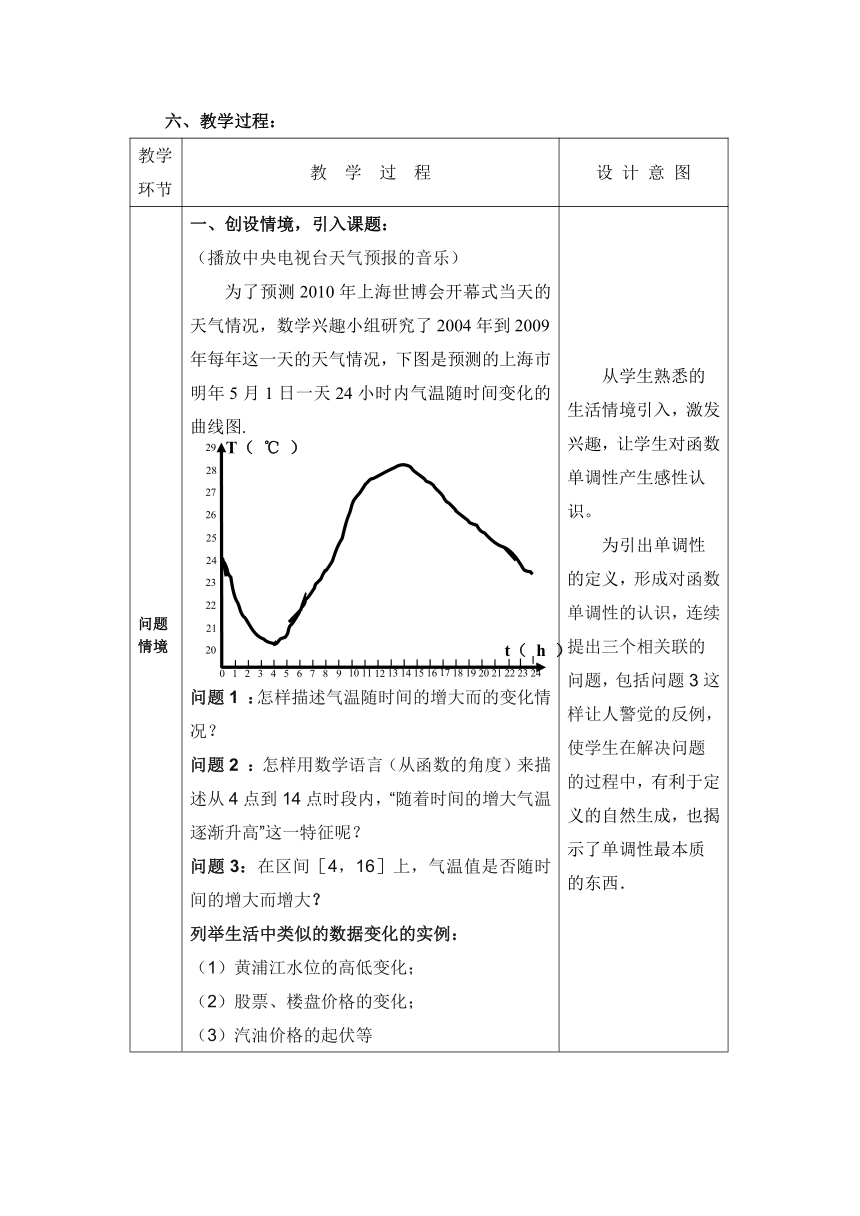
问题情境 一、创设情境,引入课题:(播放中央电视台天气预报的音乐)为了预测2010年上海世博会开幕式当天的天气情况,数学兴趣小组研究了2004年到2009年每年这一天的天气情况,下图是预测的上海市明年5月1日一天24小时内气温随时间变化的曲线图.问题1 :怎样描述气温随时间的增大而的变化情况?问题2 :怎样用数学语言(从函数的角度)来描述从4点到14点时段内,“随着时间的增大气温逐渐升高”这一特征呢?问题3:在区间[4,16]上,气温值是否随时间的增大而增大?列举生活中类似的数据变化的实例:(1)黄浦江水位的高低变化;(2)股票、楼盘价格的变化;(3)汽油价格的起伏等 从学生熟悉的生活情境引入,激发兴趣,让学生对函数单调性产生感性认识。为引出单调性的定义,形成对函数单调性的认识,连续提出三个相关联的问题,包括问题3这样让人警觉的反例,使学生在解决问题的过程中,有利于定义的自然生成,也揭示了单调性最本质的东西.
定义形成 二、借助图像,直观感知:问题4:根据下列函数的图像,说出随着自变量x的增大,函数值y的变化规律?(1);(2)。问题5:能不能根据自己的理解说说什么是单调增函数、什么是单调减函数呢? 从图象直观感知函数单调性,完成对函数单调性的第一次认识。
三、抽象思维,形成概念:问题6:如何根据函数解析式,用数学语言从“数”的角度来说明函数在上为增函数?问题7:如何用准确的数学语言表述出单调增函数的定义呢 我们一起来学习它的定义。(学生类比得出单调减函数的定义)教师介绍单调性和单调区间的定义. 通过问题的分解,引导学生步步深入,把对单调性的认识由感性上升到理性认识的高度,完成对概念的第二次认识。让学生由特殊到一般,从具体到抽象归纳形成单调性的定义。也给出了证明单调性的方法,为第三阶段的学习做好铺垫。这里体现以学生为主体,师生互动合作的教学新理念.
定义运用 四、巩固概念,应用提高:1、口答:你能找出问题情境的气温图中的单调区间吗?2、判断:(1)函数f(x)=2有单调区间。(2)定义在上的函数满足,则是上的单调增函数。3、证明:例1、运用函数单调性的定义证明:函数在区间上是增函数。(教师板书)问题8:你能归纳运用定义法探求并证明函数单调性的步骤吗?①取值;②作差;③变形;④定号;⑤下结论。例2、运用函数单调性的定义证明:函数在上的单调性。(学生完成)问题9:函数在定义域R上是单调函数吗?能用我们今天学习的函数单调性定义说说为什么吗?问题10:能说说函数的单调性情况吗?问题11:如何说明一个函数在某个区间上是单调函数?又如何说明一个函数在某个区间上不是单调函数呢? 通过对判断题的辨析,加深学生对定义的理解,完成对概念的第三次认识。回归定义,从“数”的角度证明单调性,使学生认识到“形”可帮助我们探索解题思路,而定义是最终解决问题的基础。初步掌握根据定义证明函数单调性的方法和步骤.
课堂小结 五、归纳小结,提高认识:(让学生谈体会与收获)1、函数单调性的定义;2、判断、证明函数单调性的方法;3、函数单调性的证明步骤;4、概念探究过程:直观到抽象、感性到理性;5、数学思想方法:数形结合。 学生交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,师生合作共同完成小结,通过学生的主体参与,使学生深切体会到本节课的主要内容和思想方法,从而实现对函数单调性认识的再次深化。
作业布置 六、课后探究:讨论函数(x>0)的单调性2、判断函数在[- 2, 3]上的单调性,并指出它的单调区间.3、二次函数在[0,+∞)是增函数,你能确定字母的值吗? 课后探究是对课堂知识的深化理解。
教学设计说明:
本节课是一节概念课,函数单调性的本质是利用代数的方法来研究函数图像的性质,如何将图形特征用严谨的数学语言来刻画是本节课的难点之一,另一难点是学生在高中阶段第一次接触代数证明,如何进行严格的推理论证并完成规范的书面表达。
围绕以上两个难点,在本节课的处理上,我着重注意了以下几个问题:
1、重视学生的亲身体验,具体体现在两个方面:①将新知识与学生的已有知识建立了联系,如:学生对一次函数、二次函数和反比例函数的认识,学生对“y随x的增大而增大”的理解;②运用新知识尝试解决新问题,如用定义证明函数的单调性。
2、重视学生发现的过程,如:充分暴露学生将函数图像(形)的特征转化为函数值(数)的特征的思维过程;充分暴露在正、反两个方面探讨活动中,学生认知结构升华、发现的过程。
3、重视学生的动手实践过程,通过对定义的解读、巩固,让学生动手去实践运用定义,通过对问题的设计,引导学生解决问题.
2009-11-9
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
20
21
22
23
24
25
26
27
28
29
T( ℃ )
t( h )
崇明县大新中学 赵晓凤
一、教学内容分析:
《函数单调性》是高级中学数学学科,上海教育出版社出版的高一年级(第一学期)第三章《函数》,第四单元《函数性质》的第二节,该课时主要学习增函数、减函数的定义,以及应用定义解决一些简单问题。
二、教材所处地位和作用:
函数的单调性是函数众多性质中的重要性质之一,在解决函数值域、定义域、不等式、比较两数大小等具体问题中均需用到函数的单调性;在本节课的教学中以函数的单调性的概念为线,它始终贯穿于整个课堂教学过程;利用函数的单调性的定义证明具体函数的单调性是对函数单调性概念的深层理解,且“作差、变形、判号、定论”的过程学生不易掌握。
学生只学过一次函数、反比例函数、正比例函数、二次函数,所以对函数的单调性研究也只能限于这几种函数,学生的现有认知结构中,能根据函数的图像观察出“随着自变量的增大函数值增大”等变化趋势,所以在教学中要充分利用好函数图像的直观性,发挥好多媒体教学的优势;同时在这一节中利用函数图像来研究函数性质的数形结合思想,将贯穿于我们整个高中数学教学。
三、教学目标的确定:
依据二期课改的理念及高中数学课程标准的要求,并结合学生的认知规律和实际特点,确定本节课教学目标如下:
知识与技能:从形与数两方面理解函数单调性的概念,初步掌握利用函数图像和定义判断、证明函数单调性的方法.
过程能力与方法:通过对函数单调性定义的探究,渗透数形结合的思想方法,培养观察、归纳、抽象的能力和语言表达能力,通过对函数单调性的证明,提高推理论证的能力。
情感态度价值观:通过知识的探究过程,培养细心观察、认真分析、严谨论证的良好思维习惯,感知从具体到抽象,从感性到理性的认知过程。
【教学重点】 函数单调性的概念的理解、判断及证明。
【教学难点】 根据定义证明函数的单调性。
由于本节内容涉及的问题都要通过函数增减性的定义来解决,因此确定本节课教学重点为函数单调性概念的理解、判断及证明,使用定义去证明函数单调性需灵活运用,故确定为本节的教学难点。
四、教法与学法:
1、教法分析:
依据目前教育发展和二期课改的精神及当前积极倡导“培养学生的探究精神和实践能力”的迫切需要。结合学生的认知水平,寓教学于情境之中,体现数学与现实生活的联系。采用“以学生为主体,以问题为中心”的问题驱动式教学模式,意在调动学生的积极性,让学生主动参与到教学活动中。为了突出重点,突破难点,在教学中采取以下措施:
从学生已有的生活经验,知识背景,精心设计一些适合学生学力的具体问题情境,逐步引导学生发现与探索,归纳出增、减函数的概念。
另外在教学过程中,从实际问题入手,利用学生的生活经验和感性认知,借助电教手段,生动直观地分析问题,从而增强学习的可接受性,同时诱导和启发学生主动学习,探究学习。
2、学法指导:
在本节课的教学中,教会学生善于观察,认真分析,最后从直观中抽象出理论和知识,使获取知识和培养能力融为一体,使学生主体地位得以实现,真正实现本节课的教学目标。
3、教学手段:
为了更形象、直观地突出重点,突破难点,增大教学容量,提高教学效率,本节课采用多媒体辅助教学。
五、教学方法:教师启发讲授,学生探究学习.
六、教学过程:
教学环节 教 学 过 程 设 计 意 图
问题情境 一、创设情境,引入课题:(播放中央电视台天气预报的音乐)为了预测2010年上海世博会开幕式当天的天气情况,数学兴趣小组研究了2004年到2009年每年这一天的天气情况,下图是预测的上海市明年5月1日一天24小时内气温随时间变化的曲线图.问题1 :怎样描述气温随时间的增大而的变化情况?问题2 :怎样用数学语言(从函数的角度)来描述从4点到14点时段内,“随着时间的增大气温逐渐升高”这一特征呢?问题3:在区间[4,16]上,气温值是否随时间的增大而增大?列举生活中类似的数据变化的实例:(1)黄浦江水位的高低变化;(2)股票、楼盘价格的变化;(3)汽油价格的起伏等 从学生熟悉的生活情境引入,激发兴趣,让学生对函数单调性产生感性认识。为引出单调性的定义,形成对函数单调性的认识,连续提出三个相关联的问题,包括问题3这样让人警觉的反例,使学生在解决问题的过程中,有利于定义的自然生成,也揭示了单调性最本质的东西.
定义形成 二、借助图像,直观感知:问题4:根据下列函数的图像,说出随着自变量x的增大,函数值y的变化规律?(1);(2)。问题5:能不能根据自己的理解说说什么是单调增函数、什么是单调减函数呢? 从图象直观感知函数单调性,完成对函数单调性的第一次认识。
三、抽象思维,形成概念:问题6:如何根据函数解析式,用数学语言从“数”的角度来说明函数在上为增函数?问题7:如何用准确的数学语言表述出单调增函数的定义呢 我们一起来学习它的定义。(学生类比得出单调减函数的定义)教师介绍单调性和单调区间的定义. 通过问题的分解,引导学生步步深入,把对单调性的认识由感性上升到理性认识的高度,完成对概念的第二次认识。让学生由特殊到一般,从具体到抽象归纳形成单调性的定义。也给出了证明单调性的方法,为第三阶段的学习做好铺垫。这里体现以学生为主体,师生互动合作的教学新理念.
定义运用 四、巩固概念,应用提高:1、口答:你能找出问题情境的气温图中的单调区间吗?2、判断:(1)函数f(x)=2有单调区间。(2)定义在上的函数满足,则是上的单调增函数。3、证明:例1、运用函数单调性的定义证明:函数在区间上是增函数。(教师板书)问题8:你能归纳运用定义法探求并证明函数单调性的步骤吗?①取值;②作差;③变形;④定号;⑤下结论。例2、运用函数单调性的定义证明:函数在上的单调性。(学生完成)问题9:函数在定义域R上是单调函数吗?能用我们今天学习的函数单调性定义说说为什么吗?问题10:能说说函数的单调性情况吗?问题11:如何说明一个函数在某个区间上是单调函数?又如何说明一个函数在某个区间上不是单调函数呢? 通过对判断题的辨析,加深学生对定义的理解,完成对概念的第三次认识。回归定义,从“数”的角度证明单调性,使学生认识到“形”可帮助我们探索解题思路,而定义是最终解决问题的基础。初步掌握根据定义证明函数单调性的方法和步骤.
课堂小结 五、归纳小结,提高认识:(让学生谈体会与收获)1、函数单调性的定义;2、判断、证明函数单调性的方法;3、函数单调性的证明步骤;4、概念探究过程:直观到抽象、感性到理性;5、数学思想方法:数形结合。 学生交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,师生合作共同完成小结,通过学生的主体参与,使学生深切体会到本节课的主要内容和思想方法,从而实现对函数单调性认识的再次深化。
作业布置 六、课后探究:讨论函数(x>0)的单调性2、判断函数在[- 2, 3]上的单调性,并指出它的单调区间.3、二次函数在[0,+∞)是增函数,你能确定字母的值吗? 课后探究是对课堂知识的深化理解。
教学设计说明:
本节课是一节概念课,函数单调性的本质是利用代数的方法来研究函数图像的性质,如何将图形特征用严谨的数学语言来刻画是本节课的难点之一,另一难点是学生在高中阶段第一次接触代数证明,如何进行严格的推理论证并完成规范的书面表达。
围绕以上两个难点,在本节课的处理上,我着重注意了以下几个问题:
1、重视学生的亲身体验,具体体现在两个方面:①将新知识与学生的已有知识建立了联系,如:学生对一次函数、二次函数和反比例函数的认识,学生对“y随x的增大而增大”的理解;②运用新知识尝试解决新问题,如用定义证明函数的单调性。
2、重视学生发现的过程,如:充分暴露学生将函数图像(形)的特征转化为函数值(数)的特征的思维过程;充分暴露在正、反两个方面探讨活动中,学生认知结构升华、发现的过程。
3、重视学生的动手实践过程,通过对定义的解读、巩固,让学生动手去实践运用定义,通过对问题的设计,引导学生解决问题.
2009-11-9
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
20
21
22
23
24
25
26
27
28
29
T( ℃ )
t( h )
