《平行线的特征》

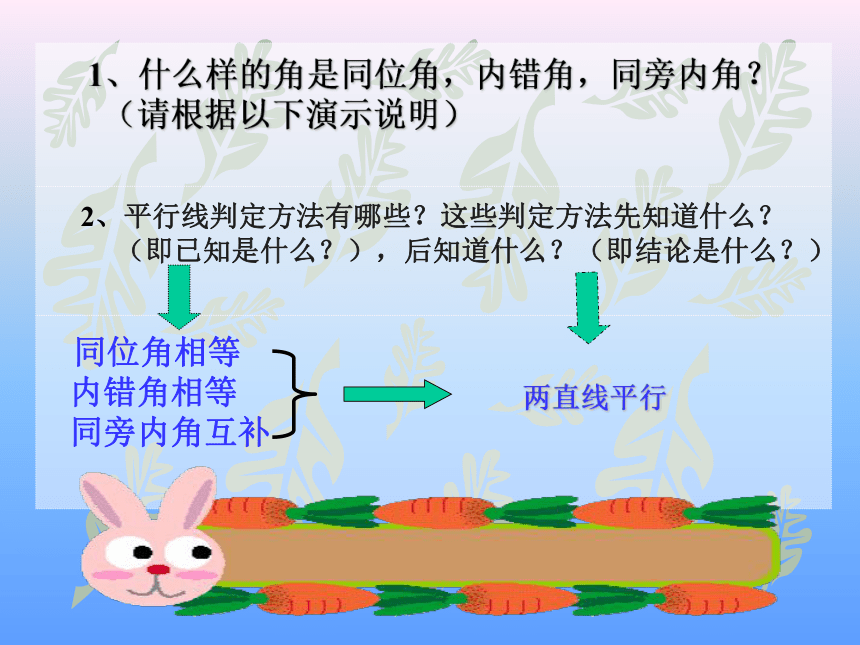
课件17张PPT。平行线的特征 1、什么样的角是同位角，内错角，同旁内角？
（请根据以下演示说明）

2、平行线判定方法有哪些？这些判定方法先知道什么？
（即已知是什么？），后知道什么？（即结论是什么？）

同位角相等
内错角相等
同旁内角互补
两直线平行复习1、判定两条直线平行有哪些方法？在这些方法中，已经知道
了什么？得到的结果是什么？2、思考：已知两条直线平行，同位角，内错角，同旁内角
有什么关系？图形已知结果结论同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
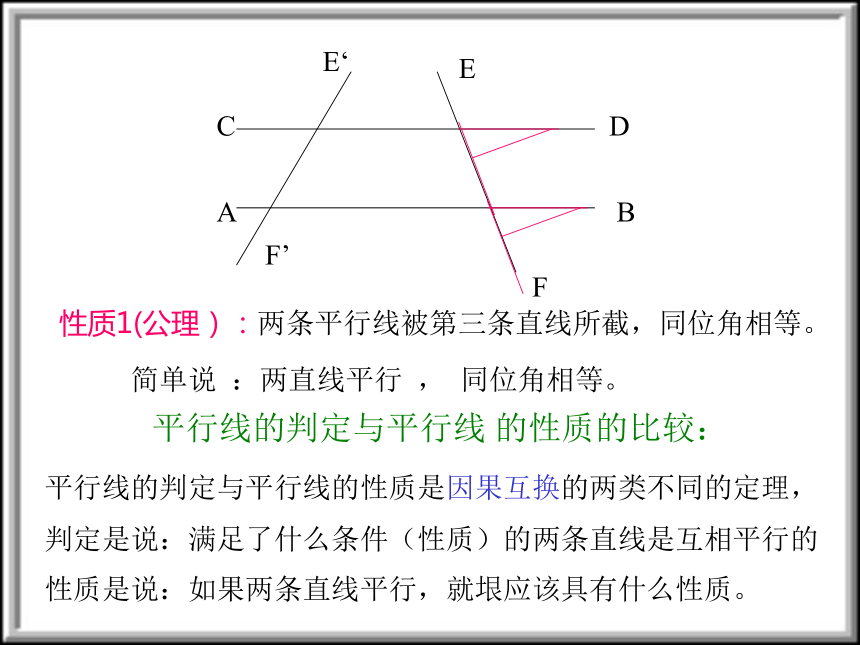
两直线平行122324））））））abababccc性质1(公理）：两条平行线被第三条直线所截，同位角相等。 简单说 ：两直线平行 ， 同位角相等。 平行线的判定与平行线 的性质的比较：CADBE‘F’EF平行线的判定与平行线的性质是因果互换的两类不同的定理，判定是说：满足了什么条件（性质）的两条直线是互相平行的性质是说：如果两条直线平行，就垠应该具有什么性质。问题如果两条直线平行，那么这两条平行线被
第三条直线所截而成的同位角有什么关系？结论平行线的性质1（公理）
两条平行线被第三条直线所截，同位角相等。
简单说成：两直线平行，同位角相等。平行线的判定公理与性质公理有什么不同比一比

a//b (已知）
?1=?2 （两直线平行，同位角相等）
又 ?1=?3（对顶角相等）
?3=?2（等量代换）
思考回答????结论如图，已知：a// b
那么?3与?2有什么关系？ 平行线的性质2
两条平行线被第三条直线所截，内错角相等
简单说成：两直线平行，内错角相等。c
解法一： a//b （已知）
? 1= ? 2（两直线平行，同位角相等）
? 1+ ? 4=180°（邻补角定义）
? 2+ ? 4=180°（等量代换）
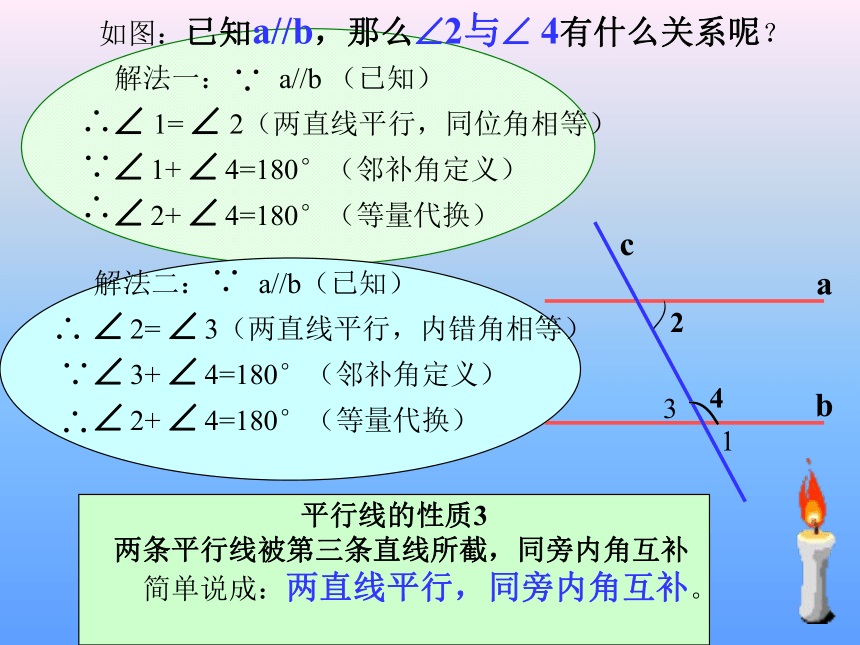
如图：已知a//b，那么?2与? 4有什么关系呢？解法二： a//b（已知）
? 2= ? 3（两直线平行，内错角相等）
? 3+ ? 4=180°（邻补角定义）
? 2+ ? 4=180°（等量代换）
平行线的性质3
两条平行线被第三条直线所截，同旁内角互补
简单说成：两直线平行，同旁内角互补。
????????能力考查1如图： ?1= ? 2（已知）
AD//
（ ）
? BCD+ ? D=180?
（ ）BC内错角相等，两直线平行两直线平行，同旁内角互补???2www.czsx.com.cn能力考查2 如图： AB//DE（已知）
? ABE+ =180?
（ ）
AB// （已知）
? DEC= ? ABC
（ ）????两直线平行，同旁内角互补两直线平行，同位角相等?DEBDE同位角相等
内错角相等
同旁内角互补两直线平行判定性质最后的冲刺图形已知结果结论同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
两直线平行122324））））））abababccc平行线的特征（性质）小结a//b同位角相等
两直线平行a//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行例题学习：例1：如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片，工作人员从玉片上已经量得∠A=1150，∠D=1000。已知梯形的两底AD//BC，请你求出另外两个角的度数。 解：∵ AD//BC （已知）.∴ ∠A＋∠B＝1800；∠C＋∠D＝1800又∵ ∠A=1150；∠D=1000. (已知)∴ ∠B＝1800－∠A＝1800－1150＝650.
∠C＝1800－∠D＝1800－1000＝800.（两直线平行，同旁内角互补）.1、如图，一条公路两次拐弯后，和原来的方向相同，也就是拐弯前后的两条路互相平行。第一次拐的角∠B等于1420，第二次拐的角∠C是多少度？为什么？课堂练习：2、如图，直线DE经过点A，DE//BC，∠B=440，∠C=570。
（1）∠DAB 等于多少度？为什么？
（2）∠DAC 等于多少度？为什么？1420？∴ DE//BC（ ）.注意：此处应用的是平行线的判定。3、已知：如图，∠ADE=600，∠B=600，∠C=800。
问∠ AED等于多少度？为什么？解：∵ ∠ADE=∠B=600 （已知）.∴ ∠AED=∠C=800 ( ).注意：此处应用的是平行线的性质。同位角相等，两直线平行两直线平行，同位角相等平行线的三个性质：两直线平行同位角相等内错角相等同旁内角互补平行线的三个判定：两直线平行同位角相等内错角相等同旁内角互补课堂小结1、平行线的三个特征（性质）：2、平行线的特征（性质）与平行线的条件（判定）的区别。 家庭作业: 教材第62页，2、3题。两直线平行，同位角相等。两直线平行，内错角相等。两直线平行，同旁内角互补。判定：性质：3、证平行，用判定。知平行，用性质。角的关系平行的关系角的关系平行的关系