13.2三角形全等的条件(2)SAS
文档属性
| 名称 | 13.2三角形全等的条件(2)SAS |  | |
| 格式 | rar | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-14 20:33:00 | ||
图片预览


文档简介
课件22张PPT。13.2三角形全等的条件(2)
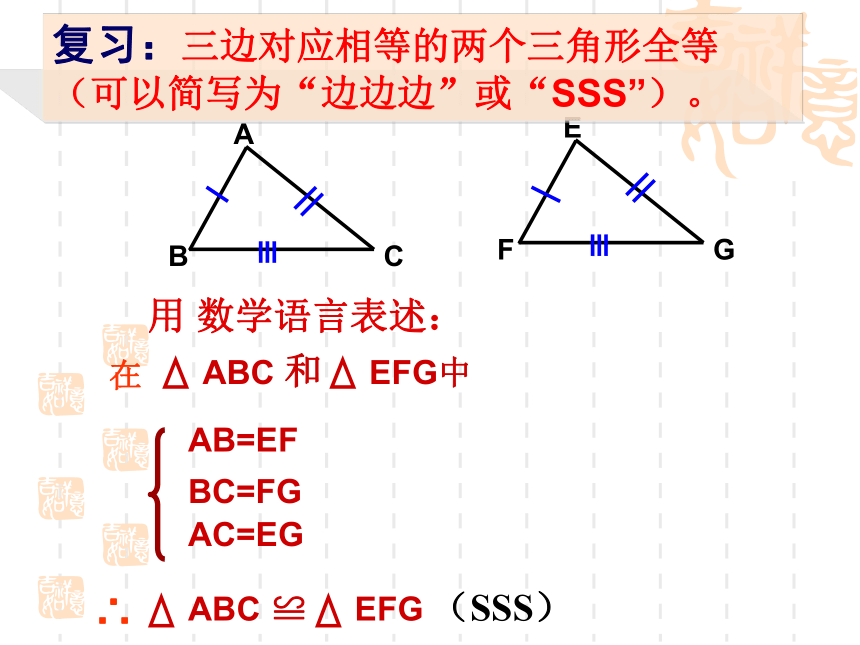
SAS初二中AB=EFBC=FGAC=EG(SSS)复习:三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。用 数学语言表述:做一做:先任意画出△ABC.再画一个△A/B/C/,
使A/B/ = AB, A/C/ = AC,∠A/=∠A.(即有两边和
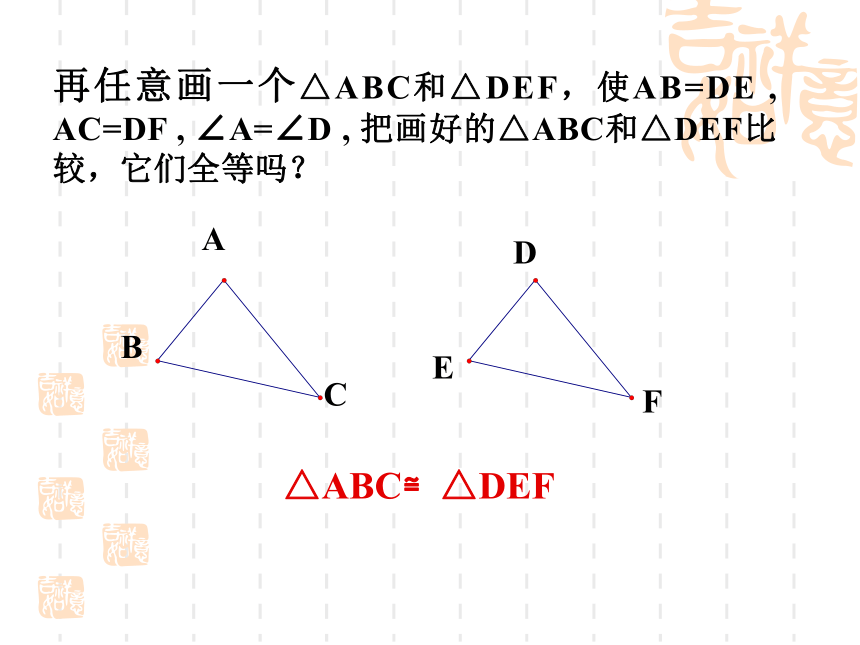
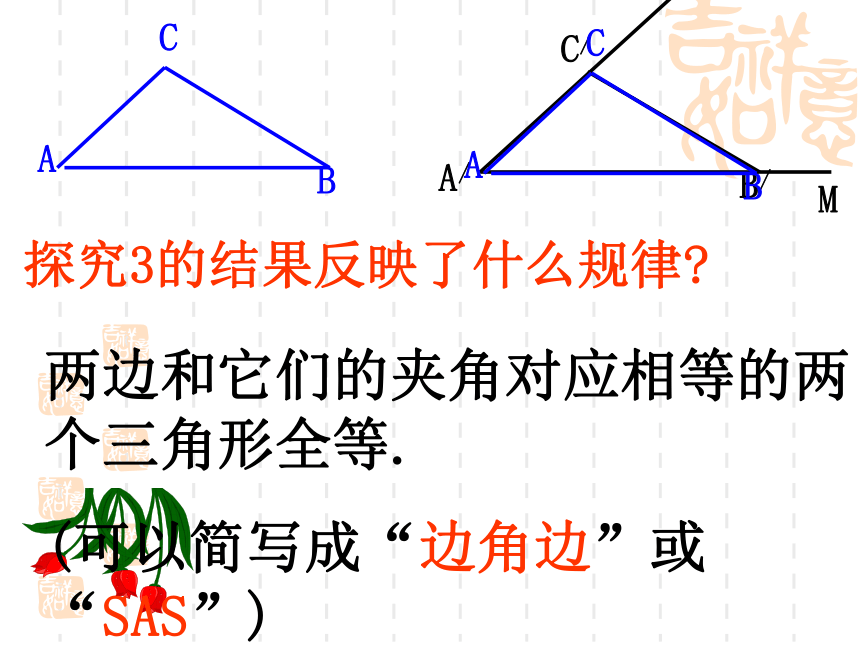
它们的夹角相等).把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?画法:2. 在射线A/ M上截取A/B/ = AB3. 在射线A/ N上截取A/C/ = AC1. 画∠MA/ N= ∠A4.连接B/ C/∴△A /B /C/就是所求的三角形探究3再任意画一个△ABC和△DEF,使AB=DE , AC=DF , ∠A=∠D , 把画好的△ABC和△DEF比较,它们全等吗?DEF△ABC≌△DEF探究3的结果反映了什么规律?两边和它们的夹角对应相等的两个三角形全等.
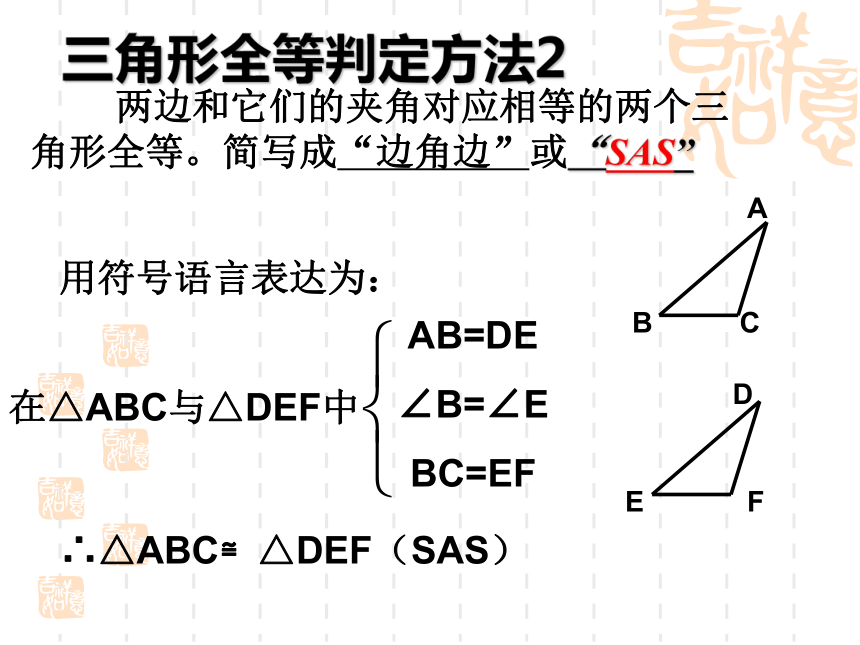
(可以简写成“边角边”或“SAS”) 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
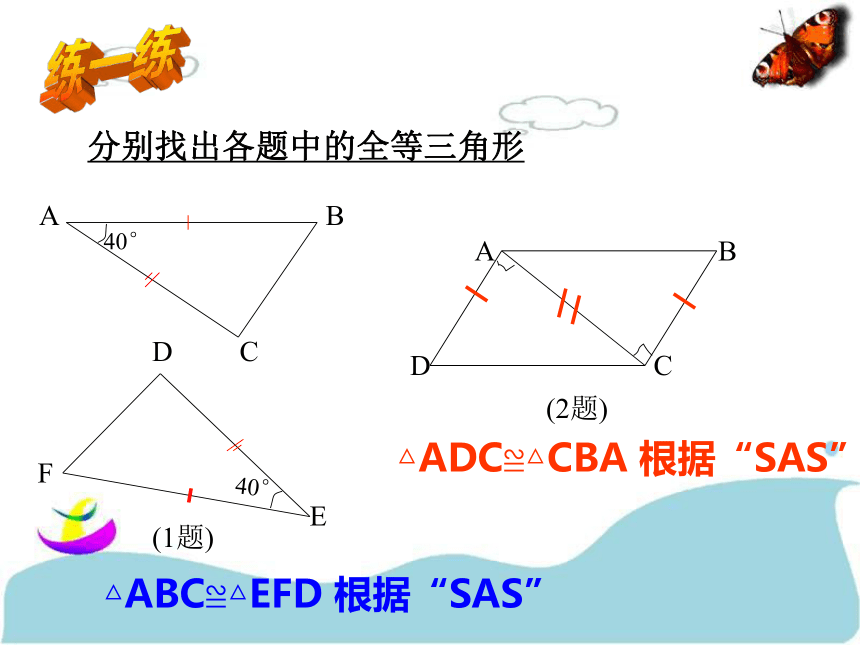
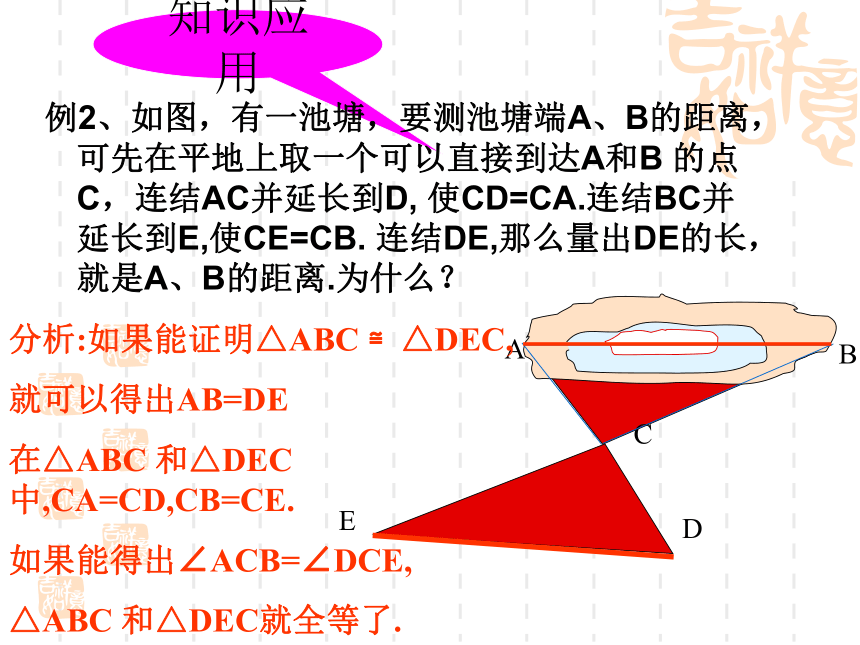
练一练分别找出各题中的全等三角形40° DEF(1题)(2题)△ABC≌△EFD 根据“SAS”△ADC≌△CBA 根据“SAS”知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?分析:如果能证明△ABC ≌△DEC,
就可以得出AB=DE
在△ABC 和△DEC中,CA=CD,CB=CE.
如果能得出∠ACB=∠DCE,
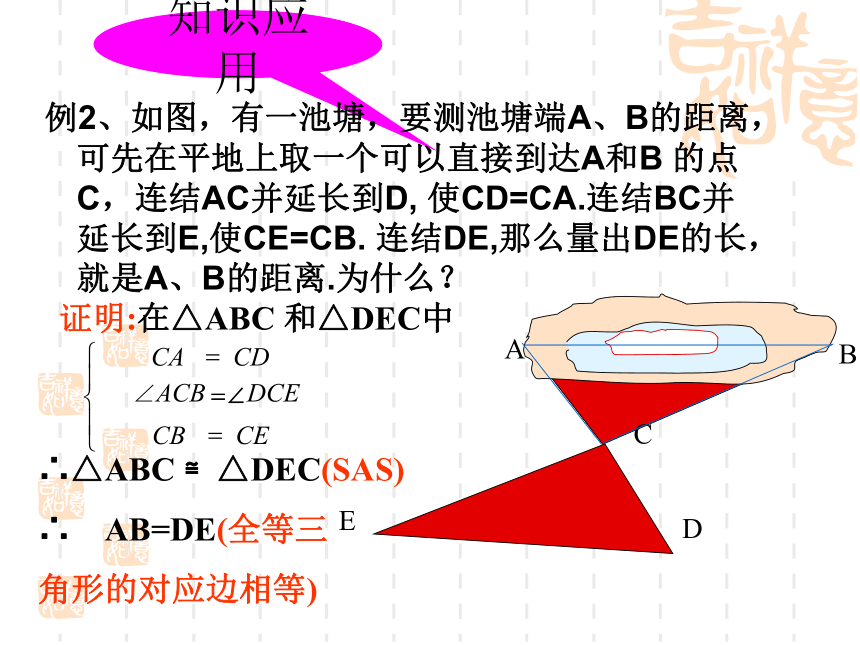
△ABC 和△DEC就全等了.知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴ AB=DE(全等三
角形的对应边相等)???íì===CECBDCE∠ACBCDCA=∠已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?例题推广证明:在△ABD与△CBD中AB=CB
∠ABD=∠CBD
BD=BD∴△ABD≌△CBD(SAS)∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。由前边两个题目可以看出: 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究4ABCD猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B他们全等吗?注:这个角一定要是这两边所夹的角ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?补充题:
例1 如图AC与BD相交于点O,
已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。证明:在△AOB和△COD中∠AOB=∠COD
OB=OD∴ △AOB≌△COD(SAS)小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH练一练1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?BDAC【证明】∵在△BAD和△BAC中,BA=BA
∠BAD=∠BAC
AD=AC则△BAD≌△BAC (SAS).即BD=BC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D要点复习与回顾:1、边角边的内容是什么?
2、边角边的作用:
(证明两个三角形全等,也可利用证明两个三角形全等进一步证明两个线段,两个角相等)
3、怎样找已知条件:
[一是已知中给出的,二是图形中隐含的(如:公共边 、公共角、对顶角、邻补角,外角等)]
总结:已知中找。图形中看 3.利用全等三角形证明线段或角相等, 是证明 线段 或角相等的重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.课堂小结:2. 用尺规作图:已知两边及其夹角的三角形1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)4.利用全等三角形解决实际问题的步骤:
⑴先确定实际问题应用哪些几何知识解决.
⑵根据实际抽象出几何图形.
⑶结合图形和题意写出已知,求证.
⑷经过分析,找出证明途径.
⑸写出证明过程.
作业:104页3、4、10补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.10cm6.5cm
SAS初二中AB=EFBC=FGAC=EG(SSS)复习:三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。用 数学语言表述:做一做:先任意画出△ABC.再画一个△A/B/C/,
使A/B/ = AB, A/C/ = AC,∠A/=∠A.(即有两边和
它们的夹角相等).把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?画法:2. 在射线A/ M上截取A/B/ = AB3. 在射线A/ N上截取A/C/ = AC1. 画∠MA/ N= ∠A4.连接B/ C/∴△A /B /C/就是所求的三角形探究3再任意画一个△ABC和△DEF,使AB=DE , AC=DF , ∠A=∠D , 把画好的△ABC和△DEF比较,它们全等吗?DEF△ABC≌△DEF探究3的结果反映了什么规律?两边和它们的夹角对应相等的两个三角形全等.
(可以简写成“边角边”或“SAS”) 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
练一练分别找出各题中的全等三角形40° DEF(1题)(2题)△ABC≌△EFD 根据“SAS”△ADC≌△CBA 根据“SAS”知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?分析:如果能证明△ABC ≌△DEC,
就可以得出AB=DE
在△ABC 和△DEC中,CA=CD,CB=CE.
如果能得出∠ACB=∠DCE,
△ABC 和△DEC就全等了.知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴ AB=DE(全等三
角形的对应边相等)???íì===CECBDCE∠ACBCDCA=∠已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?例题推广证明:在△ABD与△CBD中AB=CB
∠ABD=∠CBD
BD=BD∴△ABD≌△CBD(SAS)∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。由前边两个题目可以看出: 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究4ABCD猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B他们全等吗?注:这个角一定要是这两边所夹的角ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?补充题:
例1 如图AC与BD相交于点O,
已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。证明:在△AOB和△COD中∠AOB=∠COD
OB=OD∴ △AOB≌△COD(SAS)小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH练一练1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?BDAC【证明】∵在△BAD和△BAC中,BA=BA
∠BAD=∠BAC
AD=AC则△BAD≌△BAC (SAS).即BD=BC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D要点复习与回顾:1、边角边的内容是什么?
2、边角边的作用:
(证明两个三角形全等,也可利用证明两个三角形全等进一步证明两个线段,两个角相等)
3、怎样找已知条件:
[一是已知中给出的,二是图形中隐含的(如:公共边 、公共角、对顶角、邻补角,外角等)]
总结:已知中找。图形中看 3.利用全等三角形证明线段或角相等, 是证明 线段 或角相等的重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.课堂小结:2. 用尺规作图:已知两边及其夹角的三角形1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)4.利用全等三角形解决实际问题的步骤:
⑴先确定实际问题应用哪些几何知识解决.
⑵根据实际抽象出几何图形.
⑶结合图形和题意写出已知,求证.
⑷经过分析,找出证明途径.
⑸写出证明过程.
作业:104页3、4、10补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.10cm6.5cm
