§1.3平行四边形、矩形、菱形、正方形的性质和判定⑴
文档属性
| 名称 | §1.3平行四边形、矩形、菱形、正方形的性质和判定⑴ |

|
|
| 格式 | rar | ||
| 文件大小 | 708.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-13 00:00:00 | ||
图片预览




文档简介
课件26张PPT。 第一章 证明(二)
平行四边形的性质(一)
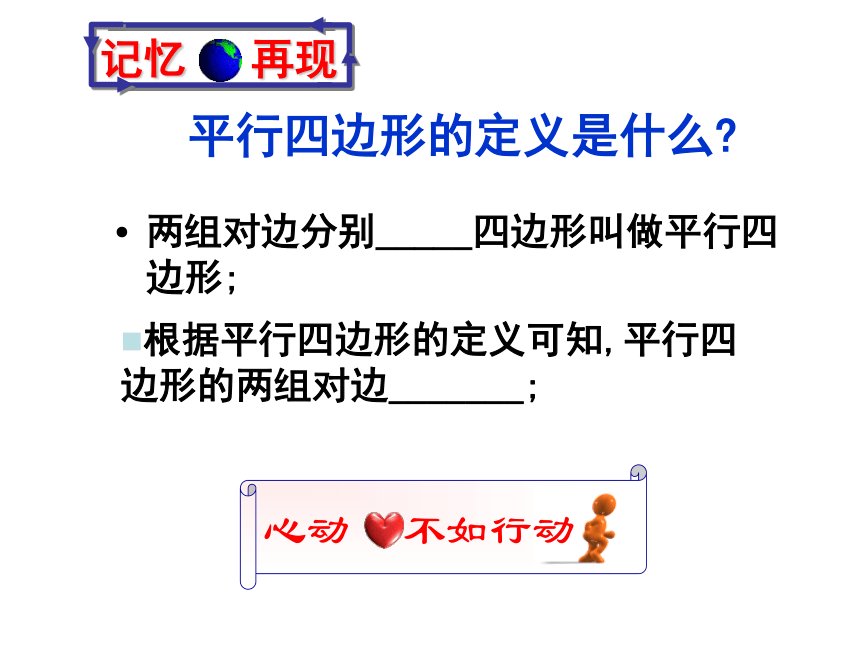
下面的图片中,有你熟悉的哪些图形?情境创设这些都是平行四边形.平行四边形的定义是什么? 两组对边分别_____四边形叫做平行四边形;记忆 再现根据平行四边形的定义可知,平行四边形的两组对边_______;再努力一下除了由定义得到的性质(两组对边分别平行),平行四边形还有哪些性质?
平行四边形的两组对边________;
平行四边形的两组对角________;
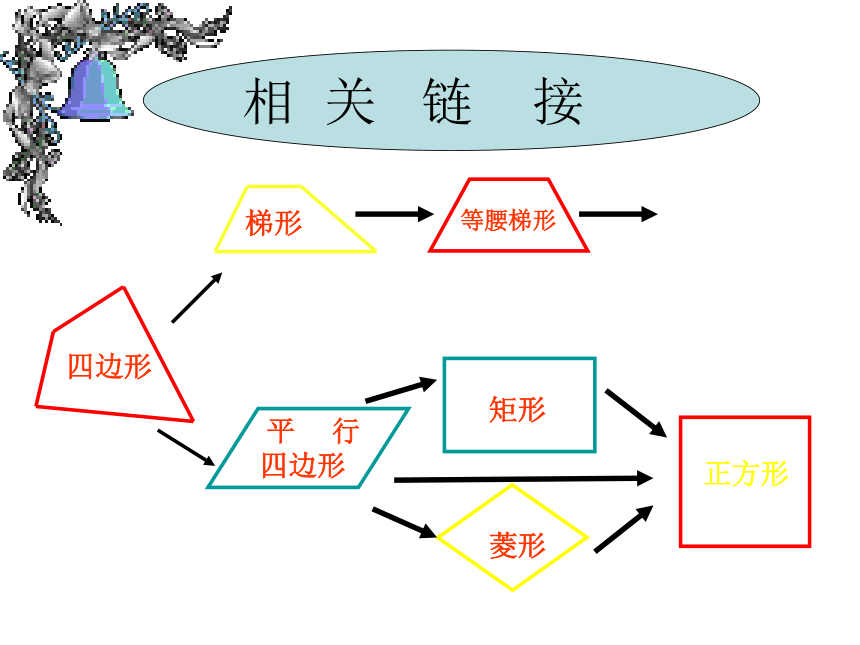
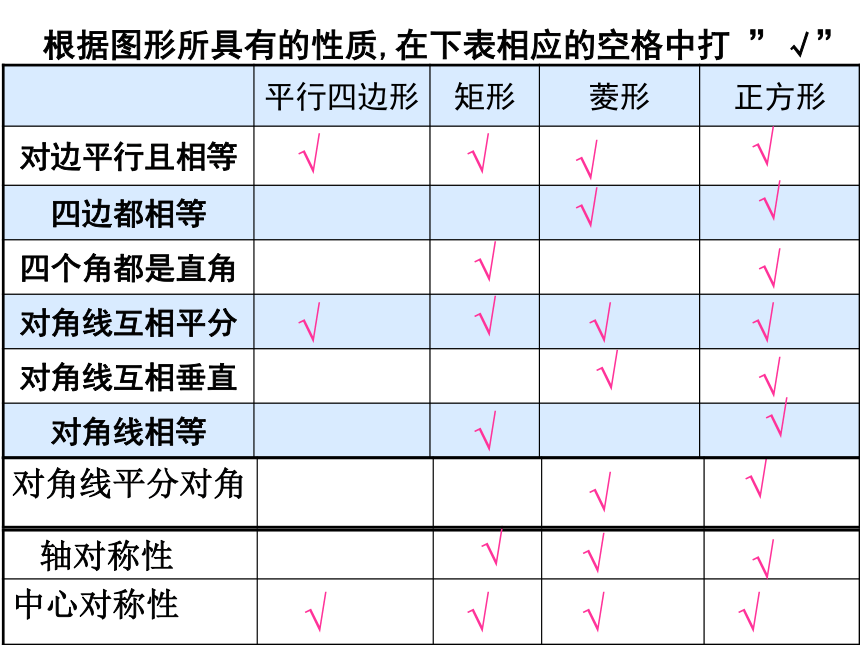
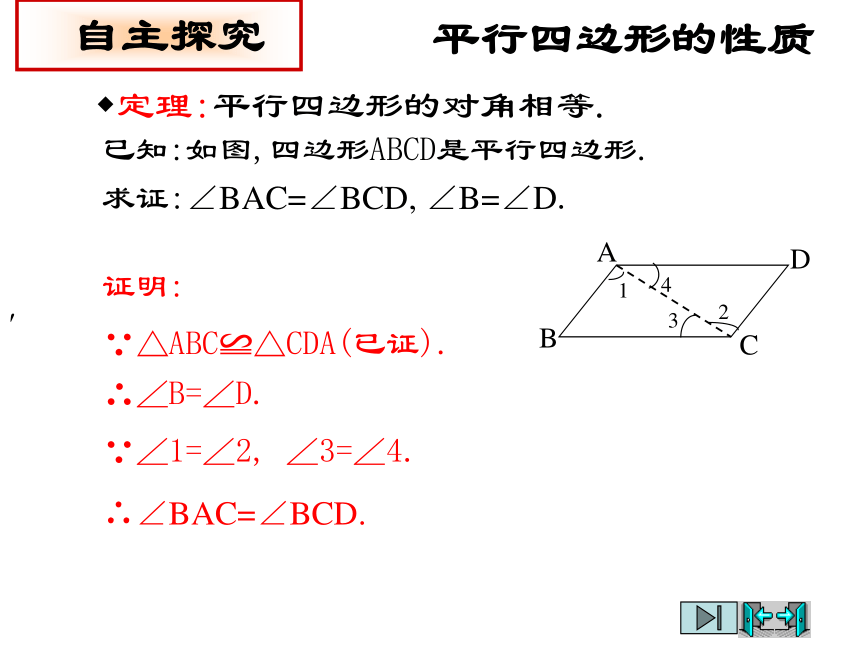
平行四边形的对角线__________;四边形梯形等腰梯形 平 行 四边形矩形菱形正方形相 关 链 接 根据图形所具有的性质,在下表相应的空格中打 ”√”√√√√√√√√√√√√√√√√√√√√√√√√√平行四边形的性质 自主探究定理:平行四边形的对边相等.已知:如图,四边形ABCD是平行四边形.求证:AB=CD,BC=DA.分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.证明:连接AC.∵四边形ABCD是平行四边形,∴AB∥CD,BC∥DA.∴∠1=∠2, ∠3=∠4.∵AC=CA,∴△ABC≌△CDA(ASA).∴AB=CD,BC=DA.从上面的证明过程,你还能得到什么结论?平行四边形的性质定理:平行四边形的对角相等.′ 自主探究已知:如图,四边形ABCD是平行四边形.求证:∠BAC=∠BCD, ∠B=∠D.∵∠1=∠2, ∠3=∠4.证明:∵△ABC≌△CDA(已证).∴∠B=∠D.∴∠BAC=∠BCD.平行四边形的性质 自主探究定理:平行四边形的对角线互相平分.已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O.求证:CO=AO,BO=DO.证明:∵四边形ABCD是平行四边形,∴BC∥DA.∵∠1=∠2, ∠3=∠4.∴BC=DA,∴△BOC≌△DOA(ASA).∴CO=AO,BO=DO.平行四边形的性质定理:平行四边形的对边相等.′ ∵ABCD是平行四边形.则AB=CD,BC=DA
定理:平行四边形的对角相等.∵ABCD是平行四边形.则∠A=∠C, ∠B=∠D.
定理:平行四边形的对角线互相平分.∵ABCD是平行四边形.
∴ CO=AO,BO=DO
1.已知:如图,□ ABCD的对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点E,F.求证:OE=OF.证明:∴OB=OD,AD∥BC.∴ ∠1=∠2.∵∠3=∠4,∴△BOF≌△DOE(ASA).∴OE=OF.∵四边形ABCD是平行四边形,点拨矫正2.已知:如图,四边形ABCD和BFDE都是平行四边形,E,F在AC上.
求证:AE=CF;点拨矫正1.选择、填空题: (1)两条对角线相等且互相垂直平分的四边形是( )
(A)平行四边形,但不是矩形 (B)矩形但不是菱形
(C)菱形但不是矩形 (D)正方形(2)下列命题为真命题的是( )
(A)四边相等的四边形是正方形.
(B)四角相等的四边形是正方形.
(C)对角线相等的菱形是正方形
(D)对角线相等且平分的四边形是正方形.才艺展示(3) 在平行四边形ABCD中,∠A=65°,则∠D的度数是 ( )
A. 105° B. 115° C. 125° D. 65°(4)已知平行四边形的周长是100cm, AB:BC=4 : 1,则AB的长为____________.(5)在平行四边形ABCD中,一个角的平分线把一条边分成3㎝和4㎝的两部分.则这个平行四边形的周长为 .(6)平行四边形的两邻边分别为3、4,那么其对角线必( )
A.大于1 B.小于7
C.大于1且小于7 D.小于7或大于1C(7)如果平行四边形的一条边长是8,一条对角线长为6,那么它的另一条对角线长m的取值范围是________________.大于10且小于22 (8)用两个全等的三角形按不同的方法拼成四边形,在这些四边形中,平行四边形的个数是( ) A.1个 B.2个 C.3个 D.4个C2、已知:如图,在□ABCD中,∠BAD和∠BCD的平分线分别交DC、BA的延长线于F、E.
求证:DE∥BF. 3、如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在对角线AC上,试问:当BE、DF满足什么条件时,EF与BD互相平分?并说明理由. FBACDE4、□ABCD的周长为32cm, ∠ABC的角平分线交边AD所在直线于点E,且AE:ED=3:2,则AB= . 拓展延伸1. □ ABCD的周长是20cm,那么它的两条邻边之和是多少?两条对角线最长不超过多少?
2.在□ ABCD中,对角线AC与BD交于O, AC=20cm ,BD=30cm,AD=18cm,则三角形BOC的周长是多少? 3.在平行四边形ABCD中,E,F分别在CD,AD上,且AE=CF,AE,CF交于点G.
求证:BG平分∠AGC.拓展延伸2、在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交BC于E,交CD于F,FG∥AB交BC于G。 求证:1、CE=CF 2、CG=EB 拓展与延伸结束寄语严格性之于数学家,犹如道德之于人.
条理清晰,因果相应,言必有据.是初学证明者谨记和遵循的原则.
平行四边形的性质(一)
下面的图片中,有你熟悉的哪些图形?情境创设这些都是平行四边形.平行四边形的定义是什么? 两组对边分别_____四边形叫做平行四边形;记忆 再现根据平行四边形的定义可知,平行四边形的两组对边_______;再努力一下除了由定义得到的性质(两组对边分别平行),平行四边形还有哪些性质?
平行四边形的两组对边________;
平行四边形的两组对角________;
平行四边形的对角线__________;四边形梯形等腰梯形 平 行 四边形矩形菱形正方形相 关 链 接 根据图形所具有的性质,在下表相应的空格中打 ”√”√√√√√√√√√√√√√√√√√√√√√√√√√平行四边形的性质 自主探究定理:平行四边形的对边相等.已知:如图,四边形ABCD是平行四边形.求证:AB=CD,BC=DA.分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.证明:连接AC.∵四边形ABCD是平行四边形,∴AB∥CD,BC∥DA.∴∠1=∠2, ∠3=∠4.∵AC=CA,∴△ABC≌△CDA(ASA).∴AB=CD,BC=DA.从上面的证明过程,你还能得到什么结论?平行四边形的性质定理:平行四边形的对角相等.′ 自主探究已知:如图,四边形ABCD是平行四边形.求证:∠BAC=∠BCD, ∠B=∠D.∵∠1=∠2, ∠3=∠4.证明:∵△ABC≌△CDA(已证).∴∠B=∠D.∴∠BAC=∠BCD.平行四边形的性质 自主探究定理:平行四边形的对角线互相平分.已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O.求证:CO=AO,BO=DO.证明:∵四边形ABCD是平行四边形,∴BC∥DA.∵∠1=∠2, ∠3=∠4.∴BC=DA,∴△BOC≌△DOA(ASA).∴CO=AO,BO=DO.平行四边形的性质定理:平行四边形的对边相等.′ ∵ABCD是平行四边形.则AB=CD,BC=DA
定理:平行四边形的对角相等.∵ABCD是平行四边形.则∠A=∠C, ∠B=∠D.
定理:平行四边形的对角线互相平分.∵ABCD是平行四边形.
∴ CO=AO,BO=DO
1.已知:如图,□ ABCD的对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点E,F.求证:OE=OF.证明:∴OB=OD,AD∥BC.∴ ∠1=∠2.∵∠3=∠4,∴△BOF≌△DOE(ASA).∴OE=OF.∵四边形ABCD是平行四边形,点拨矫正2.已知:如图,四边形ABCD和BFDE都是平行四边形,E,F在AC上.
求证:AE=CF;点拨矫正1.选择、填空题: (1)两条对角线相等且互相垂直平分的四边形是( )
(A)平行四边形,但不是矩形 (B)矩形但不是菱形
(C)菱形但不是矩形 (D)正方形(2)下列命题为真命题的是( )
(A)四边相等的四边形是正方形.
(B)四角相等的四边形是正方形.
(C)对角线相等的菱形是正方形
(D)对角线相等且平分的四边形是正方形.才艺展示(3) 在平行四边形ABCD中,∠A=65°,则∠D的度数是 ( )
A. 105° B. 115° C. 125° D. 65°(4)已知平行四边形的周长是100cm, AB:BC=4 : 1,则AB的长为____________.(5)在平行四边形ABCD中,一个角的平分线把一条边分成3㎝和4㎝的两部分.则这个平行四边形的周长为 .(6)平行四边形的两邻边分别为3、4,那么其对角线必( )
A.大于1 B.小于7
C.大于1且小于7 D.小于7或大于1C(7)如果平行四边形的一条边长是8,一条对角线长为6,那么它的另一条对角线长m的取值范围是________________.大于10且小于22 (8)用两个全等的三角形按不同的方法拼成四边形,在这些四边形中,平行四边形的个数是( ) A.1个 B.2个 C.3个 D.4个C2、已知:如图,在□ABCD中,∠BAD和∠BCD的平分线分别交DC、BA的延长线于F、E.
求证:DE∥BF. 3、如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在对角线AC上,试问:当BE、DF满足什么条件时,EF与BD互相平分?并说明理由. FBACDE4、□ABCD的周长为32cm, ∠ABC的角平分线交边AD所在直线于点E,且AE:ED=3:2,则AB= . 拓展延伸1. □ ABCD的周长是20cm,那么它的两条邻边之和是多少?两条对角线最长不超过多少?
2.在□ ABCD中,对角线AC与BD交于O, AC=20cm ,BD=30cm,AD=18cm,则三角形BOC的周长是多少? 3.在平行四边形ABCD中,E,F分别在CD,AD上,且AE=CF,AE,CF交于点G.
求证:BG平分∠AGC.拓展延伸2、在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交BC于E,交CD于F,FG∥AB交BC于G。 求证:1、CE=CF 2、CG=EB 拓展与延伸结束寄语严格性之于数学家,犹如道德之于人.
条理清晰,因果相应,言必有据.是初学证明者谨记和遵循的原则.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
