§1.3平行四边形、矩形、菱形、正方形的性质和判定⑵
文档属性
| 名称 | §1.3平行四边形、矩形、菱形、正方形的性质和判定⑵ |  | |
| 格式 | rar | ||
| 文件大小 | 614.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-13 11:21:00 | ||
图片预览




文档简介
课件19张PPT。§3.2特殊的平行四边形第1课时—矩形的性质及判定主备人:李志勇 审核人:程伟伟平行四边形的性质 ①两组对边分别平行
②两组对边分别相等 ①对角相等②邻角互补 对角线互相平分夹在两条平行线间的平行线段相等 回顾 思考矩形的性质定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的
定义,利用对角
相等,邻角互补
可使问题得证.证明:∵ 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,
∠B=1800-∠A=900,
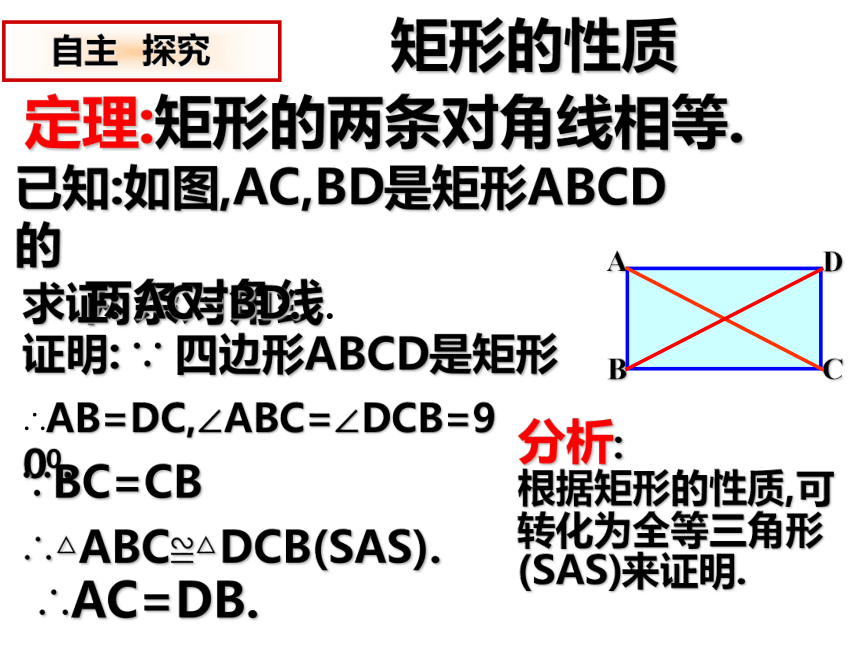
∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.即:矩形的四个角都是直角. 自主探究定理:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的
两条对角线.求证: AC=BD.证明:∵ 四边形ABCD是矩形∴AB=DC,∠ABC=∠DCB=900.分析:
根据矩形的性质,可转化为全等三角形(SAS)来证明.∵BC=CB∴△ABC≌△DCB(SAS).∴AC=DB.矩形的性质 自主 探究议一议:设矩形的对角线AC与BD交于点E,
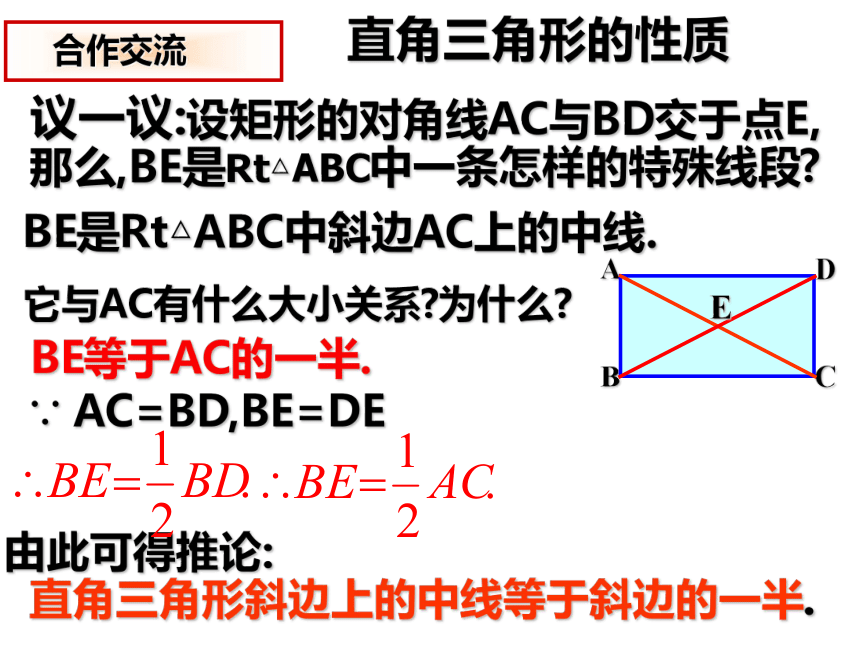
那么,BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么? 由此可得推论:
直角三角形斜边上的中线等于斜边的一半.BE是Rt△ABC中斜边AC上的中线. BE等于AC的一半.∵ AC=BD,BE=DE 合作交流直角三角形的性质E知识 总结矩形的性质,推论:定理:矩形的四个角都是直角.推论(直角三角形性质):
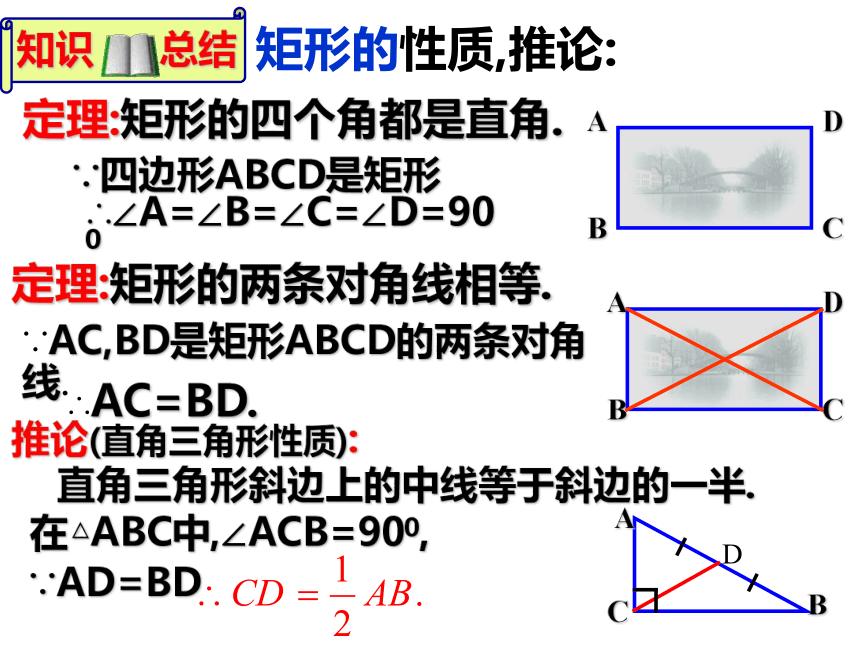
直角三角形斜边上的中线等于斜边的一半.∵四边形ABCD是矩形∴∠A=∠B=∠C=∠D=900∵AC,BD是矩形ABCD的两条对角线.∴AC=BD.在△ABC中,∠ACB=900,
∵AD=BD定理:矩形的两条对角线相等. 求证:如果一个三角形一边上的中线等于这边
的一半,那么这个三角形是直角三角形.求证:△ABC是直角三角形已知:CD是△ABC边AB上的中线,且证明:延长CD到E,使DE=DC,连接AE,BE.∴四边形ACBE是平行四边形.∵AB=2CD,CE=2CD,∴ AB=CE.∴平行四边形ACBE是矩形.∵ AD=BD,CD=ED,∴∠ACB=900.∴△ABC是直角三角形. 点拨矫正你怎样证明?还有别的方法吗?1 .矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等 2.下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直
3.由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
才艺展示4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 A.50° B.60° C.70° D.80°6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于 A.30° B.45° C.60° D.120°[ ][ ][ ]7. 已知矩形的一条对角线与一边的夹
角是40°,则两条对角线所夹锐角的
度数为 ( ) A.50° B.60°
C.70° D.80°才艺展示8.如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)△BEC是 三角形;
(2)若AB=1,∠ABE=45°, 则BC= .矩形性质的应用9.已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.O 才艺 展示 才艺展示10.已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别平分
∠DAB和∠CBA,QP∥AD,交AB于点Q.
(1)求证:AP⊥PB;
(2)如果AD=5cm,AP=8cm,那么AB的长是多少?
△APB的面积是多少?11.已知:如图,BD、CE是△ABC 的两条高,M是BC的中点. 求证:ME=MD 才艺展示 1.在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在E处.设DE与BC相交于点F,求BF的长.拓展延伸 2.矩形ABCD中,DF平分∠ADC,交AC于E,交BC于F, ∠BDF=15°,求∠DOC和∠COF的度数.拓展提高
3.如图 在矩形ABCD中,BE平分∠ABC,
交CD于点E,点F在边BC上,
① 如果FE⊥AE,求证FE=AE。②如果FE=AE 你能证明FE⊥AE吗?拓展提高再见
②两组对边分别相等 ①对角相等②邻角互补 对角线互相平分夹在两条平行线间的平行线段相等 回顾 思考矩形的性质定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的
定义,利用对角
相等,邻角互补
可使问题得证.证明:∵ 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,
∠B=1800-∠A=900,
∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.即:矩形的四个角都是直角. 自主探究定理:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的
两条对角线.求证: AC=BD.证明:∵ 四边形ABCD是矩形∴AB=DC,∠ABC=∠DCB=900.分析:
根据矩形的性质,可转化为全等三角形(SAS)来证明.∵BC=CB∴△ABC≌△DCB(SAS).∴AC=DB.矩形的性质 自主 探究议一议:设矩形的对角线AC与BD交于点E,
那么,BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么? 由此可得推论:
直角三角形斜边上的中线等于斜边的一半.BE是Rt△ABC中斜边AC上的中线. BE等于AC的一半.∵ AC=BD,BE=DE 合作交流直角三角形的性质E知识 总结矩形的性质,推论:定理:矩形的四个角都是直角.推论(直角三角形性质):
直角三角形斜边上的中线等于斜边的一半.∵四边形ABCD是矩形∴∠A=∠B=∠C=∠D=900∵AC,BD是矩形ABCD的两条对角线.∴AC=BD.在△ABC中,∠ACB=900,
∵AD=BD定理:矩形的两条对角线相等. 求证:如果一个三角形一边上的中线等于这边
的一半,那么这个三角形是直角三角形.求证:△ABC是直角三角形已知:CD是△ABC边AB上的中线,且证明:延长CD到E,使DE=DC,连接AE,BE.∴四边形ACBE是平行四边形.∵AB=2CD,CE=2CD,∴ AB=CE.∴平行四边形ACBE是矩形.∵ AD=BD,CD=ED,∴∠ACB=900.∴△ABC是直角三角形. 点拨矫正你怎样证明?还有别的方法吗?1 .矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等 2.下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直
3.由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
才艺展示4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 A.50° B.60° C.70° D.80°6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于 A.30° B.45° C.60° D.120°[ ][ ][ ]7. 已知矩形的一条对角线与一边的夹
角是40°,则两条对角线所夹锐角的
度数为 ( ) A.50° B.60°
C.70° D.80°才艺展示8.如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)△BEC是 三角形;
(2)若AB=1,∠ABE=45°, 则BC= .矩形性质的应用9.已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.O 才艺 展示 才艺展示10.已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别平分
∠DAB和∠CBA,QP∥AD,交AB于点Q.
(1)求证:AP⊥PB;
(2)如果AD=5cm,AP=8cm,那么AB的长是多少?
△APB的面积是多少?11.已知:如图,BD、CE是△ABC 的两条高,M是BC的中点. 求证:ME=MD 才艺展示 1.在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在E处.设DE与BC相交于点F,求BF的长.拓展延伸 2.矩形ABCD中,DF平分∠ADC,交AC于E,交BC于F, ∠BDF=15°,求∠DOC和∠COF的度数.拓展提高
3.如图 在矩形ABCD中,BE平分∠ABC,
交CD于点E,点F在边BC上,
① 如果FE⊥AE,求证FE=AE。②如果FE=AE 你能证明FE⊥AE吗?拓展提高再见
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
