§1.3平行四边形、矩形、菱形、正方形的性质和判定⑸
文档属性
| 名称 | §1.3平行四边形、矩形、菱形、正方形的性质和判定⑸ |  | |
| 格式 | rar | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-13 11:30:00 | ||
图片预览



文档简介
课件19张PPT。平行四边形的判定主备人:李志勇 复核人:郭红霞 小明在家用细木棒钉制了一个平行四边形。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
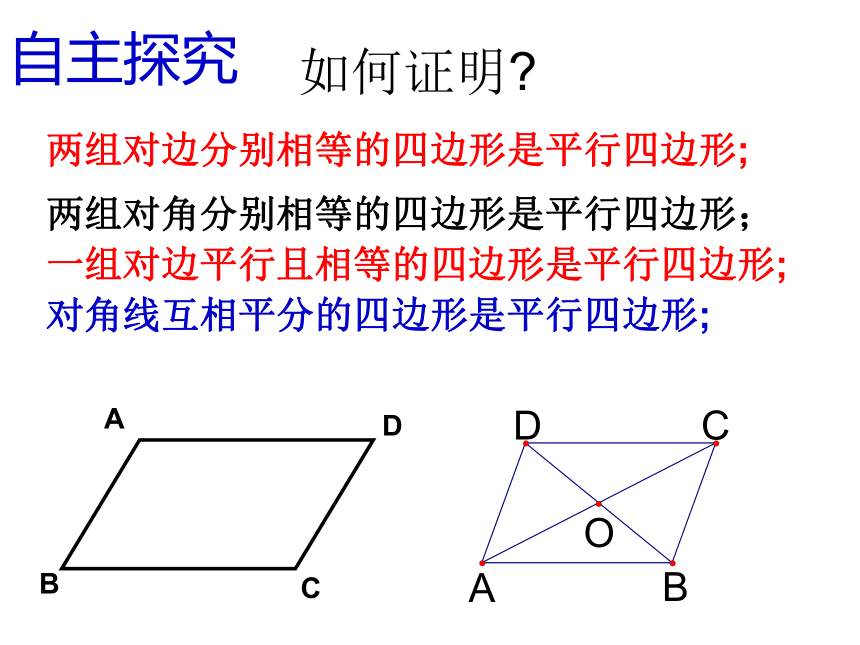
大家都困惑了……请你帮忙情境创设平行四边形的判定方法 两组对边分别相等的四边形是 平行四边形 两组对边分别平行的四边形是平行四边形。方法 一:方法 二:∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形∵AB=CD,AD=BC ∴四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形 两条对角线互相平分的四边形是平行四边形。 两组对角分别相等的四边形是平行四边形方法 三:方法 四:方法五:∵∠A=∠C,∠B=∠D ∴四边形ABCD是平行四边形∵OA=OC,OB=OD ∴四边形ABCD是平行四边形∵ AB∥CD,AB=CD ∴四边形ABCD是平行四边形如何证明?两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
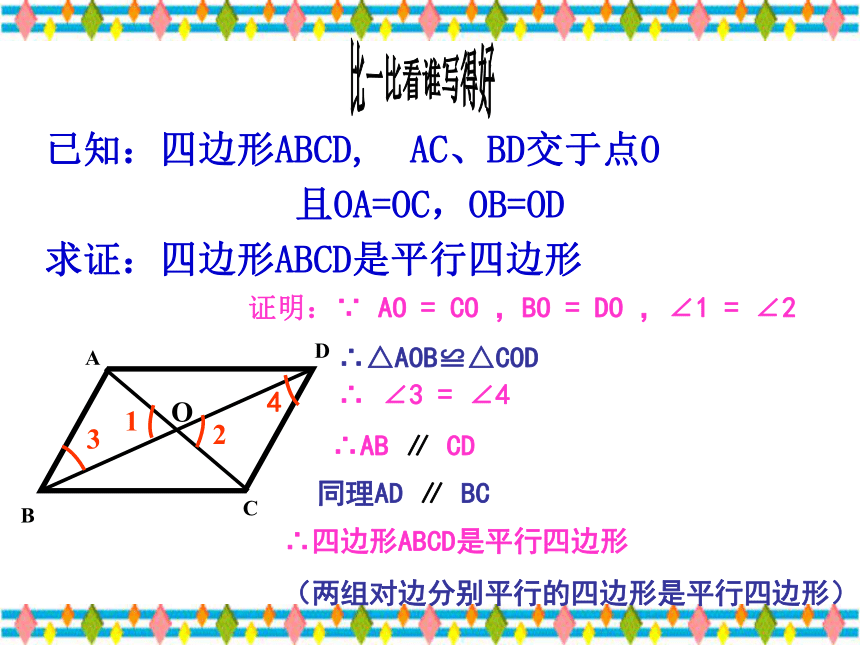
对角线互相平分的四边形是平行四边形;自主探究已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形比一比看谁写得好证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
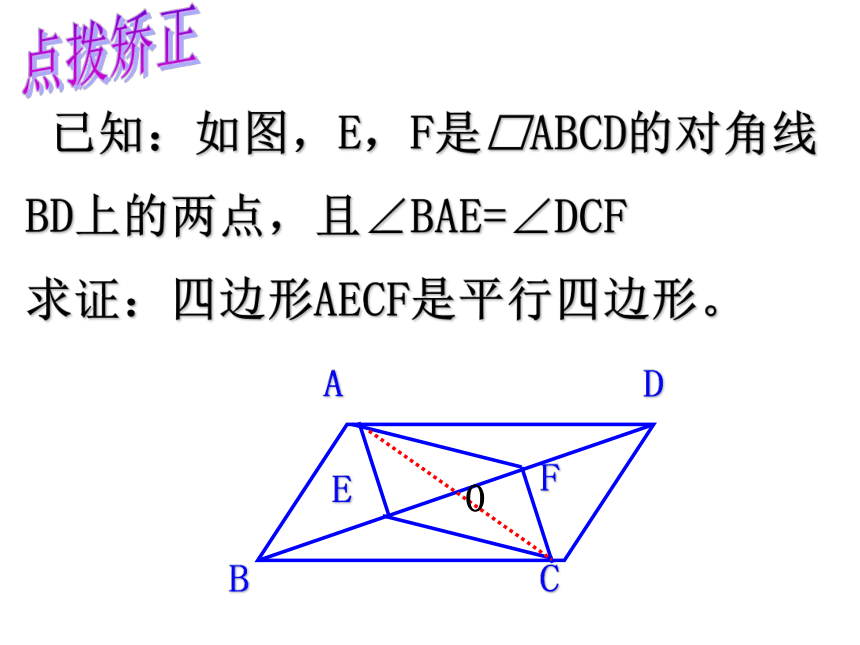
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4 已知:如图,E,F是□ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。O点拨矫正才艺展示:1、判断下列说法是否正确。
(1)一组对边平行,另一组对边相等的四边形一定是平行四边形。
(2)对角线相等的四边形是平行四边形。
(3)两组对边分别相等的四边形是平行四边形。
(4)有两条边相等,并且另
外的两条边也相等的四边形
一定是平行四边形。筝形2.判断下列四边形是不是平行四边形?才艺展示:3.在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C才艺展示:4.在四边形ABCD中,若分别给出四个条件:⑴AB∥CD ⑵AB=CD ⑶AD=BC ⑷AD∥ BC,现在以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号,写出所有情况)才艺展示:5.已知:在平行四边形ABCD中,对角线AC 、BD相交于点O,E是AB的中点, AB=6, BC=8 ,∠ABC= 70°,则OE=____, ∠OEB= ____°.E才艺展示:才艺展示:6、在□ABCD中,E,F,G,H分别是四条边上的点,且满足AE=CF,BG=DH,求证:四边形EFGH是平行四边形。7、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形才艺展示: 1、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD123拓展延伸2:如图,在△ABC中,AB=14,BC=18,BD是AC边上的中线,求BD的取值范围。3、如图所示,在 Rt△ABC中,∠ACB= 90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
⑴ 求证:四边形ACEF是平行四边形;
⑵ 当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
⑶ 四边形ACEF有可能是正方形吗?为什么?本课学到了什么?1.定义:两组对边分别_____的四边形叫做平行四边形;
2.两组对边分别_____的四边形是平行四边形;
3.两组对角分别____的四边形是平行四边形;
4.一组对边____且____的四边形是平行四边形;
5.对角线_____的四边形是平行四边形;回顾思考
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙情境创设平行四边形的判定方法 两组对边分别相等的四边形是 平行四边形 两组对边分别平行的四边形是平行四边形。方法 一:方法 二:∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形∵AB=CD,AD=BC ∴四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形 两条对角线互相平分的四边形是平行四边形。 两组对角分别相等的四边形是平行四边形方法 三:方法 四:方法五:∵∠A=∠C,∠B=∠D ∴四边形ABCD是平行四边形∵OA=OC,OB=OD ∴四边形ABCD是平行四边形∵ AB∥CD,AB=CD ∴四边形ABCD是平行四边形如何证明?两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形;自主探究已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形比一比看谁写得好证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4 已知:如图,E,F是□ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。O点拨矫正才艺展示:1、判断下列说法是否正确。
(1)一组对边平行,另一组对边相等的四边形一定是平行四边形。
(2)对角线相等的四边形是平行四边形。
(3)两组对边分别相等的四边形是平行四边形。
(4)有两条边相等,并且另
外的两条边也相等的四边形
一定是平行四边形。筝形2.判断下列四边形是不是平行四边形?才艺展示:3.在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C才艺展示:4.在四边形ABCD中,若分别给出四个条件:⑴AB∥CD ⑵AB=CD ⑶AD=BC ⑷AD∥ BC,现在以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号,写出所有情况)才艺展示:5.已知:在平行四边形ABCD中,对角线AC 、BD相交于点O,E是AB的中点, AB=6, BC=8 ,∠ABC= 70°,则OE=____, ∠OEB= ____°.E才艺展示:才艺展示:6、在□ABCD中,E,F,G,H分别是四条边上的点,且满足AE=CF,BG=DH,求证:四边形EFGH是平行四边形。7、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形才艺展示: 1、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD123拓展延伸2:如图,在△ABC中,AB=14,BC=18,BD是AC边上的中线,求BD的取值范围。3、如图所示,在 Rt△ABC中,∠ACB= 90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
⑴ 求证:四边形ACEF是平行四边形;
⑵ 当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
⑶ 四边形ACEF有可能是正方形吗?为什么?本课学到了什么?1.定义:两组对边分别_____的四边形叫做平行四边形;
2.两组对边分别_____的四边形是平行四边形;
3.两组对角分别____的四边形是平行四边形;
4.一组对边____且____的四边形是平行四边形;
5.对角线_____的四边形是平行四边形;回顾思考
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
