§1.3平行四边形、矩形、菱形、正方形的性质和判定⑻
文档属性
| 名称 | §1.3平行四边形、矩形、菱形、正方形的性质和判定⑻ |

|
|
| 格式 | rar | ||
| 文件大小 | 266.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-13 00:00:00 | ||
图片预览





文档简介
课件15张PPT。正方形判定主备人:李志勇 复核人:郭红霞复习与回顾1、正方形的定义是什么?
有一个角是直角的菱形是正方形
有一组邻边相等的矩形是正方形
2、正方形有什么性质?
(1)四条边都相等;
(2)四个角都是直角;
(3)对角线相等且互相垂直平分,…… 正方形的判定方法一、从正方形的定义:
1.有一个角是直角的菱形是正方形
2.有一组邻边相等的矩形是正方形
二、从正方形的性质:
判断下列命题是否正确,错误的请举出反例,正确的给出证明。
1.四条边都相等的四边形是正方形
2.四个角都是直角的四边形是正方形
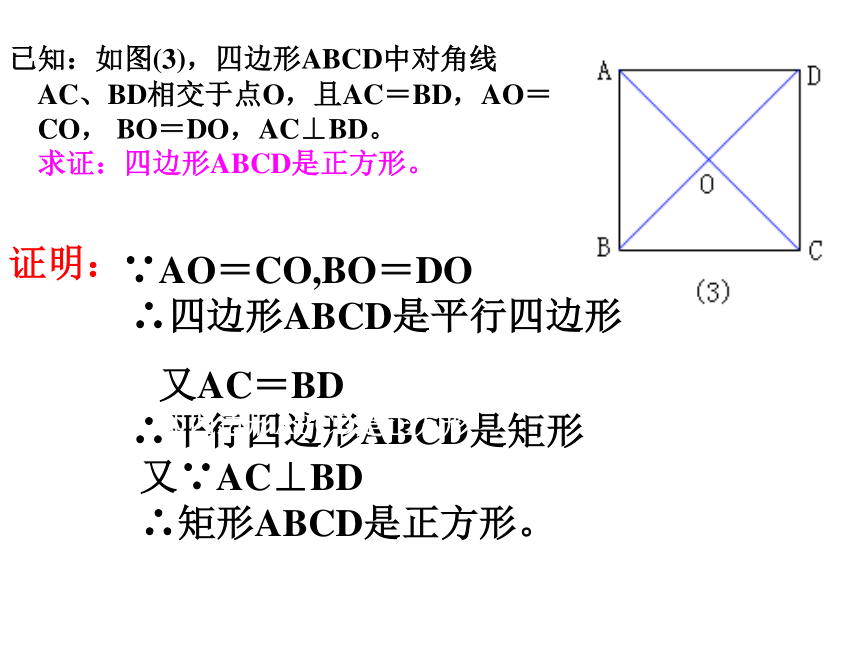
3.对角线相等且互相垂直平分的四边形是正 方形 求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
AC、BD相交于点O,且AC=BD,
AO=CO,BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。 请大家先根据题意,画出图形然后写出已知、求证。点拨矫正求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
证明:
∵AO=CO,BO=DO ∴四边形ABCD是平行四边形 又AC=BD ∴平行四边形ABCD是矩形 又∵AC⊥BD ∴矩形ABCD是正方形。即四边形ABCD是正方形 AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。 求证:四边形ABCD是正方形。
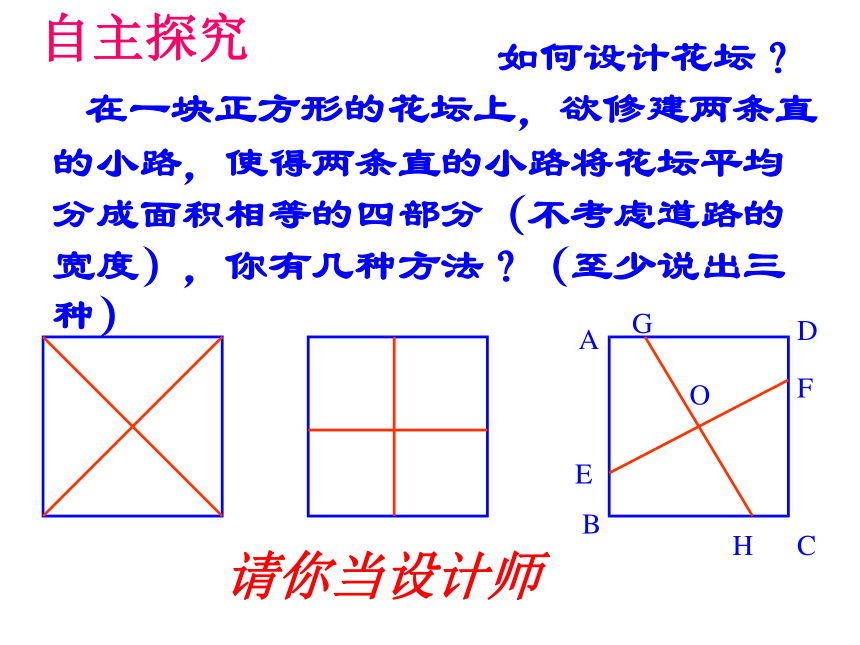
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师ABCDEFGHO自主探究 1.四个内角都相等的四边形一定是: A.正方形 B.菱形 C.矩形 D.平行四边形 2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是: A.AO=BO=CO=DO,AC⊥BD
B.AD∥BC ∠A=∠C
C.AO=CO BO=DO AB=BC D.AC=BD 3 .四个内角都相等,四条边也都相等的四边形一定是: A.正方形 B.菱形
C.矩形 D.平行四边形 才艺展示 E F4、正方形ABCD的边长为4,P是形内任一点,求⊿PAB与⊿PCD的面积之和。ABCDP提示:过P作PE⊥AB于E,
并延长EP交CD于F.
可求得面积之和S=8.才艺展示5:已知正方形ABCD中,Q在CD上,且DQ=QC,P在BC上,AP=CD+CP; 求证: AQ平分∠DAP.A D
Q
B P C E证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形,
∴AD=CD,AD∥CD;
∴∠D=∠QCE,∠DAQ=∠E,
又∵DQ=CQ,
∴⊿ADQ≌⊿ECQ (AAS).
∴AD=CE,又AD=CD,
∴CD=CE, ∴AP=CD+CP=CE+CP=EP.
∴∠PAQ=∠E
∴∠DAQ=∠PAQ,即AQ平分∠DAQ.才艺展示 6.△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F. 求证: 四边形CFDE是正方形.才艺展示 7.已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。才艺展示1.如图,在△ABC中,∠C=90°,∠BAC、∠ABC的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.
求证: 四边形CFDE是正方形.H拓展延伸2.如图,正方形ABCD中,E、F分别是CD、AD上的一点,EF=AF+CE。求∠EBF的度数。ABCDFE拓展延伸3.(2001年山东省济南市中考试题)如图,是一块在电脑屏幕上出现的矩形色块图,由5种颜色不同的正方形组成。设中间最小的一个正方形边长为1,则这个矩形的面积是拓展延伸收获与反思
有一个角是直角的菱形是正方形
有一组邻边相等的矩形是正方形
2、正方形有什么性质?
(1)四条边都相等;
(2)四个角都是直角;
(3)对角线相等且互相垂直平分,…… 正方形的判定方法一、从正方形的定义:
1.有一个角是直角的菱形是正方形
2.有一组邻边相等的矩形是正方形
二、从正方形的性质:
判断下列命题是否正确,错误的请举出反例,正确的给出证明。
1.四条边都相等的四边形是正方形
2.四个角都是直角的四边形是正方形
3.对角线相等且互相垂直平分的四边形是正 方形 求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
AC、BD相交于点O,且AC=BD,
AO=CO,BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。 请大家先根据题意,画出图形然后写出已知、求证。点拨矫正求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
证明:
∵AO=CO,BO=DO ∴四边形ABCD是平行四边形 又AC=BD ∴平行四边形ABCD是矩形 又∵AC⊥BD ∴矩形ABCD是正方形。即四边形ABCD是正方形 AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。 求证:四边形ABCD是正方形。
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师ABCDEFGHO自主探究 1.四个内角都相等的四边形一定是: A.正方形 B.菱形 C.矩形 D.平行四边形 2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是: A.AO=BO=CO=DO,AC⊥BD
B.AD∥BC ∠A=∠C
C.AO=CO BO=DO AB=BC D.AC=BD 3 .四个内角都相等,四条边也都相等的四边形一定是: A.正方形 B.菱形
C.矩形 D.平行四边形 才艺展示 E F4、正方形ABCD的边长为4,P是形内任一点,求⊿PAB与⊿PCD的面积之和。ABCDP提示:过P作PE⊥AB于E,
并延长EP交CD于F.
可求得面积之和S=8.才艺展示5:已知正方形ABCD中,Q在CD上,且DQ=QC,P在BC上,AP=CD+CP; 求证: AQ平分∠DAP.A D
Q
B P C E证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形,
∴AD=CD,AD∥CD;
∴∠D=∠QCE,∠DAQ=∠E,
又∵DQ=CQ,
∴⊿ADQ≌⊿ECQ (AAS).
∴AD=CE,又AD=CD,
∴CD=CE, ∴AP=CD+CP=CE+CP=EP.
∴∠PAQ=∠E
∴∠DAQ=∠PAQ,即AQ平分∠DAQ.才艺展示 6.△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F. 求证: 四边形CFDE是正方形.才艺展示 7.已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。才艺展示1.如图,在△ABC中,∠C=90°,∠BAC、∠ABC的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.
求证: 四边形CFDE是正方形.H拓展延伸2.如图,正方形ABCD中,E、F分别是CD、AD上的一点,EF=AF+CE。求∠EBF的度数。ABCDFE拓展延伸3.(2001年山东省济南市中考试题)如图,是一块在电脑屏幕上出现的矩形色块图,由5种颜色不同的正方形组成。设中间最小的一个正方形边长为1,则这个矩形的面积是拓展延伸收获与反思
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
