27.1 图形的相似
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二十六章二次函数
第19课时 §27.1 图形的相似
同学们在上册已经学习了图形的全等,与全等图形相比,形状相同的图形不仅是现实世界运动变化的最简捷形式之一,而且是现实生活中更为广泛存在的现象(全等图形其实就是它的一个特例).现实世界中既有图形的全等变换,也有图形的相似变换,事实上,探索相似图形的一些重要性质,不仅是认识、描述物体的形状,更好地刻画现实世界的必要手段,而且也是解决现实世界中的具体问题,进行数学交流的重要工具.
本章是继“图形全等、三角形全等”之后集中研究图形形状的内容,不仅是对图形全等内容的进一步深化和发展,而且是对图形研究方法的综合运用.学习本章有关内容,不仅是第三学段“图形的认识”、“图形与变换”等部分的重要目标,而且也是密切数学与现实之间必然联系以及“图形与空间”各部分之间内在联系的重要桥梁.因此,学好本章的内容十分重要.我们来看下面的问题:
1.小颖测得2m高的标杆在太阳下的影长为1.2m,同时又
测得一棵树的影长为3.6m,请你帮助小颖计算出这棵树的高度.
2.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,
某一时刻AB在阳光下的投影BC=3m.
(1)请你在图4.1中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光
下的投影长为6m,请你计算DE的长
相信,通过本章的学习,上述问题是不难解决的.
点击一:线段的比的定义
(1)线段比的概念:在同一单位下,两条线段长度的比.叫做这两条线段的比.
(2)比例线段的定义:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段.简称比例线段,如四条线段a,b,c,d,有,那么这四条线段叫做成比例线段.
(3)比例尺:在地图或者工程图纸上,图上长度与实际长度的比通常叫做比例尺.如你照的全身照片与你本人相比,缩小了很多,若用1:20表示,则把比例尺称为1:20.
(4)比例的基本性质:如果,那么ad=bc(a,b,c,d都不为零).特例:若,那么b2=ac,则把b叫做a,c的比例中项.
(5)比例性质的推广:
针对练习1:
1. 如图2,直线CD∥EF,若OC=3,CE=4,则的值是( )
A. B. C. D.
答案:C
2. 已知A、B两地的实际距离是5km,画在图上的距离为2cm,则该地图的比例尺为
A.2:5 B.1:2500 C.250000:1 D. 1:250000
答案:D
点击二:相似形的概念
(1)定义:一般地说:形状相同的两个图形称为相似图形.从所学习的多边形而言:对应角相等,对应边成比例的两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
(2)相似多边形写法:用符号“∽”表示,读作“相似于”.
相似形定义应注意两点:(1)相同点:形状相同;(2)不同点:大小不一定相同.
点击三:相似形的识别
形状相同识识别图形相似的重要标致.
通过生活中的实例认识物体和图形的相似;感受形状相同是识别图形相似的重要标致.理解相似图形概念;会判断两个图形是否相似.
相似形与全等形的联系与区别:全等形是相似形的特殊情况.全等一定相似,但相似不一定全等.
点击四: 相似形的性质
相似形的对应边相等,对应角相等.
点击五:相似多边形的性质
相似多边形的对应边成比例,对应角相等;反之,如果两个多边形的对应角相等,对应边成比例,那么这两个多边形相似.两个边数不同的多边形一定不相似,仅有对应角相等(如正方形与矩形)或仅有对应边成比例(如正方形与菱形)的多边形并不一定相似.
针对练习:
1.如图1,点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是( ).
A. B. C. D.
答案:A
2.在下列四组图形中,不相似的有 ( )
A.1组 B.2组 C.3组 D.4组
答:B
3.若如图4所示的两个四边形相似,则的度数是( ).
A. B. C. D.
答:A
4.将一个矩形纸片ABCD沿AD和BC的中点的连线对折,要使矩形AEFB与原矩形相似,
则原矩形的长和宽的比应为( ).
A.2:1 B. C. D.1:1
答:C
类型之一:图形相似和相似图形的概念
例1: 下面是两张大小不同的中国地图,左边的图形与右边的图形有怎样的关系?
【解析】左边的中国地图图形可以看作是右边的中国地图图形缩小得来的.由于不同的需要,经常会制成各种大小的中国地图地图,但其形状(包括地图中所描绘的各个部分)肯定是相同的.
答案:这两幅地图相似.
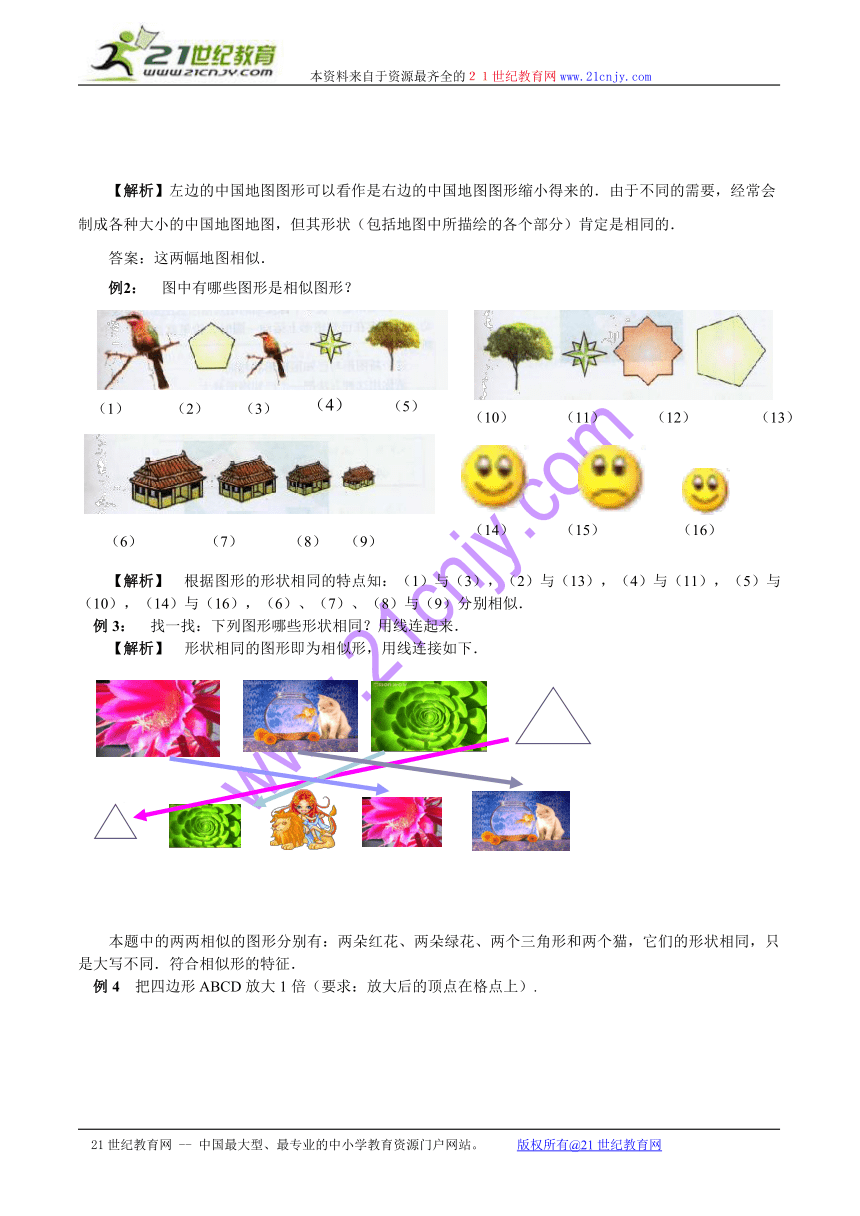
例2: 图中有哪些图形是相似图形?
【解析】 根据图形的形状相同的特点知:(1)与(3),(2)与(13),(4)与(11),(5)与(10),(14)与(16),(6)、(7)、(8)与(9)分别相似.
例3: 找一找:下列图形哪些形状相同?用线连起来.
【解析】 形状相同的图形即为相似形,用线连接如下.
本题中的两两相似的图形分别有:两朵红花、两朵绿花、两个三角形和两个猫,它们的形状相同,只是大写不同.符合相似形的特征.
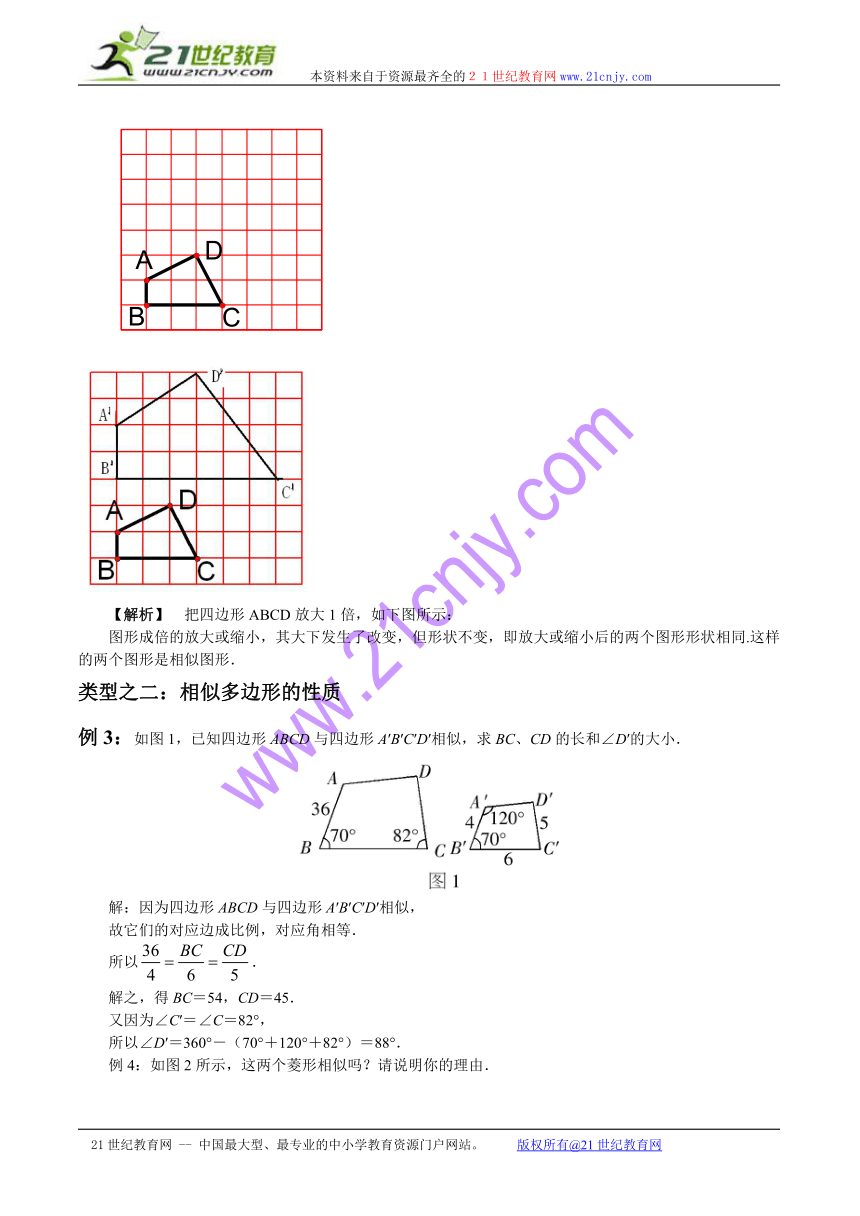
例4 把四边形ABCD放大1倍(要求:放大后的顶点在格点上).
【解析】 把四边形ABCD放大1倍,如下图所示:
图形成倍的放大或缩小,其大下发生了改变,但形状不变,即放大或缩小后的两个图形形状相同.这样的两个图形是相似图形.
类型之二:相似多边形的性质
例3:如图1,已知四边形ABCD与四边形A′B′C′D′相似,求BC、CD的长和∠D′的大小.
解:因为四边形ABCD与四边形A′B′C′D′相似,
故它们的对应边成比例,对应角相等.
所以.
解之,得BC=54,CD=45.
又因为∠C′=∠C=82°,
所以∠D′=360°-(70°+120°+82°)=88°.
例4:如图2所示,这两个菱形相似吗?请说明你的理由.
解:这两个菱形不相似.因为这两个菱形的对应角不相等,第一个菱形的内角分别为45°,135°,45°,135°,而第二个菱形的内角分别为60°,120°,60°,120°,它们仅对应边成比例.
例5: 已知图3中的两个梯形相似,求未知边x、y、z的长度和∠α、∠β的度数.
分析:解题时要充分利用相似多边形的特征和梯形的性质.
解:因为两个梯形相似,
所以.
解之,得x=3,y=6,z=3.
又因为对应角相等,
所以∠α=∠D=180°-∠A=180°-62°=118°,
∠β=∠B′=180°-∠C′=180°-110°=70°.
一.选择题
1.下列各线段的长度成比例的是( )毛
A.2cm,5cm,6cm,8cm B.1cm,2cm,3cm,4cm
C.3cm,6cm,7cm,9cm D.3cm,6cm,9cm,18cm
2.已知A,B两地的实际距离是250米,若画在图上的距离是5厘米, 则图上距离与实际距离的比是( )
A.1:50 B.1:5000 C.1:500 D.1:50000
3.下列语句中不正确的是( ).
(A)求两条线段的比值,必需采用相同的长度单位
(B)求两条线段的比值,只需采用相同的长度单位,与选用何种长度单位无关
(C)两个相似三角形中,任意两组边对应成比例
(D)不相似的两个三角形中,也有可能两组边对应成比例
4.下列各组图形有可能不相似的是( ).
(A)各有一个角是50°的两个等腰三角形;(B)各有一个角是100°的两个等腰三角形
(C)各有一个角是50°的两个直角三角形;(D)两个等腰直角三角形
5.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面( )
(A)2.4米 (B)2.8米 (C)3米 (D)高度不能确定
6.下列语句正确的是( )毛
A.在△ABC和△A′B′C′中,∠B=∠B′=90°, ∠A=30°,
∠C′=60°, 则△ABC和△A′B′C′不相似;
B.在△ABC和△A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,
B′C′=14,A′B ′=10,则△ABC∽△A′B′C′;
C.两个全等三角形不一定相似; D.所有的菱形都相似
7.如图所示, △ABC∽△ADE,AE=30cm,EC=15cm,BC=60cm,则DE的长为( )
A.40cm B.50cm C.45cm D.35cm
8.如图所示,能保证△ACD∽△ABC的条件是( )
A.AB:BC=AC:CD B.CD:AD=BC:AC
C.CD2=AD.DC D.AC2=AB.AD
9.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为( )
A.9:4 B.2:3 C.3:2 D.81:16
10.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是( )
11.等边三角形的一条中线与一条中位线长的比是( )
A. :1; B.:2; C.:; D.1:3
12.如图所示,在□ABCD中,BE交AC,CD于G,F,交AD的延长线于E, 则图中的相似三角形有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
1.已知:.(1)当a=1时,b=___,c=____;(2)当a≠0时 ,=_______.
2.两个相似三角形的一组对应边长分别为15和27,它们的周长之差为36,则较小三角形的周长是 .
3.若一个边长为10cm的等边三角形ABC内接一个正方形DEFG,且点D,E在BC边上,点F,G分别在AC,AB边上,则正方形DEFG的边长是_____.
4.如果一个三角形的面积根据相似的知识扩大9倍,那么它的周长扩大________倍.
5.如图所示, △ABC中,DE∥FG∥BC,且AD=DF=FB,则
S△AFG:S△ABC=_______.
6.在矩形ABCD中,AB=3BC,P为DC上任意一点,使得
△ADP与△PBC相似的点P有________个.
三、解答题
1.任意画一个三角形,再把它放大到原来的3倍.
2.如图所示,铁道口的栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米时, 长臂端点升高了几米
3.将矩形纸片ABCD沿折痕EF对折,使点A与C重合.若已知AB=6cm,BC=8cm,求EF的长.
4.已知:正方形的边长为1.
(1)如图(1)所示,可以算出一个正方形的对角线长为 , 那么两个正方形并排拼成的矩形的对角线的长呢 n个正方形并排拼成的矩形的对角线长呢
(2)根据图(2),说明△BCE∽△BED;
(3)由图(3),在下列所给的3个结论中, 通过合理推理选出一个正确的结论加以说明.
(A)∠BEC+∠BDE=45°; (B)∠BEC+∠BED=45°; (C)∠BEC+∠DFE=45°.
5.如图所示,已知凸透镜焦距 =10cm,一根点燃的蜡烛放在距凸透镜15cm的主光轴上,现测得烛焰AB长为2cm,通过调节光屏位置,得到烛焰在光屏上清晰的像.
(1)请根据凸透镜成像原理(与主光轴平行的光线经过凸透镜折射后,通过凸透镜的焦点,经过凸透镜光心的光线不改变方向),画出烛焰的像的位置;
(2)求出烛焰像的长度.
6.如图所示,有一条路CF为15米宽,这条路的北侧有一栋11层高的楼AB, 为33米的高层住宅,这条路的南侧有一栋电力公司办公楼CD,为12米高, 已知高层住宅的每层楼都一样高,当某一时刻,高层住宅楼的影长是165米,办公楼的影子映在住宅楼上,使下面的几层没有见到阳光,请你通过计算说明此刻高层住宅从第几层开始没有被前面的办公楼档住阳光.
答案:
一、DBCAA BADCB AD
二、1.2,3,3 2.45 3.(20-30)CM; 4.3 5.4:9 6.3
三、1.略 2.8米 3.15/2 (先求得OC=5,再由△COE∽△CBA求得OE=5/4)
4.(1), (2)解:由BE=,BC=1,BD=2,
∴, 且∠EBD=135°,
∴△BCE∽△BED.
(3)解:由(2)知,△BCE∽∽BED,有∠BEC=∠BED, ∠BCE=∠BED,
又∠BEC+∠BCE=45°,∴∠BEC+∠BED=45°,
所以(B)成立.
HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4
∴△BEC∽△DEF,∴∠BCE=∠DFE,
又∠BEC+ ∠BCE=45°,∴∠BEC+∠DFE=45°,所以(C)成立.
5. (1)略, (2)4cm; 24.略.毛
6.解:过E作EM⊥CD于M,设EF=x,则DM=12-x.
由题意知:,∴x=9.
又33 米高的楼是11层,
∴1层楼为3米高,因此EF是3层楼高.
∴从第4 层开始没有被前面的办公楼挡住阳光.
一、认认真真,书写快乐
1.两个相似图形的 相同, 不一定相同.
2.放大镜下看到的物体图形与原来的图形 相似图形(填“是”或“不是”)
3.在中国地理地图册上,连接上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图1所示.飞机从台湾直飞上海的距离为1 286千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是 千米.
4.科学研究表明,当人的下肢长与身高之比为0.618时,看起来最美.某成年女士身高为155cm,下肢长94cm,按此比例,该女士穿的高跟鞋鞋跟的最佳高度应约为 cm(精确到0.1)
5.在比例尺为1∶m的地图上,某市为长5cm,宽为2cm的矩形地域,则该市的实际地域面积为 平方米.
二、仔仔细细,记录自信
6.下面每组图中的两个图形是相似图形的是( )
7.下面每组图中的两个图形不是相似图形的是( )
8.下列说法错误的是( )
A.同一底片冲洗出的一张一寸照片和一张两寸照片相似
B.大小不一的两张中国地图相似
C.一个人在哈哈镜中的形象与他本人是相似的
D.国旗上的大小五角星相似
9.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB之比为( )
A.3∶4 B.2∶3 C.3∶5 D.1∶2
10.应中共中央总书记胡锦涛同志的邀请,中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的“大唐芙蓉园”.该园占地面积约为800 000m2,若按比例尺1∶2 000缩小后,其面积大约相当于( )
A.一个篮球场的面积
B.一张乒乓球台台面的面积
C.《人民日报》的一个版面的面积
D.《数学》课本封面的面积
三、平心静气,展示智慧
11.一块长3m,宽1.5m的矩形黑板如图2所示,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?
12.我们已经学习了相似三角形,也知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.
现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.
参考答案:
一、1.形状,大小 2.是 3.3 858 4.4.7 5.
二、6.B 7.D 8.C 9.A 10.C
三、11.答:不相似,因为对应边不成比例.
12.圆和正六边形是相似图形,因为它们的形状相同;菱形和长方形不是相似图形,因为它们的形状不一定相同.
1.如图,在正方形网格中,每个小正方形的边长均为1个单位.将向下平移4个单位,得到,再把绕点顺时针旋转,得到,请你画出和(不要求写画法).
【解析】 先将向下平移4个单位,得到,再把绕点顺时针旋转,得到,结果如图所示:
本题融图形的平移、旋转于一体,综合性、操作性强,主要考查学生实际动手操作能力.由于平移、旋转不改变图形的大小,故平移、旋转后的三角形与原三角形的关系全等,是属于相似的特例.
2.如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点D顺时针方向旋转900,1800,2700的图案,
你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为l,旋转后点A的对应点依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.
【解析】 (1)如图,正确画出图案
(2)如图,=-4
=(3+5)2-4××3×5
=34
故四边形似AA1A2A3的面积为34.
(3)结论:AB2+BC2=AC2或勾股定理的文字叙述
课时作业:
A等级
一、选择题
1.下面图形中,相似的一组是( )
A B C D
2.下面给出的图形中,不是相似的图形的是( )
A.刚买的一双手套的左右两只 B.仅仅宽度不同的两快长方形木板
C.一对羽毛球球拍 D.复印出来的两个“春”字
3. 在下列四组图形中,不相似的有( )
A.1组 B.2组 C.3组 D.4组
4. 如图,下列四组图形中,两个图形不相似的有( )
A.1组 B.2组 C.3组 D.4组
5.你看到过哈哈镜吗?哈哈镜中的形象与你本人相似的识( )
A B C D
6.a、b、c、d是四条线段,下列各组中这四条线段成比例的是 ( )
A.a=2cm, b=5cm, c=5cm, d=10cm
B.a=5cm, b=3cm, c=5cm, d=3cm
C.a=30cm, b=2cm, c=0.8cm, d=2cm
D.a=5cm, b=0.02cm, c=7cm, d=0.3cm
7.下列图形中一定相似的一组是 ( )
A.邻边对应成比例的两个平行四边形 B.有一条边相等的两个矩形
C.有一个内角相等的两个菱形 D.底角都是600的两个等腰三角形
8.根据下列各组条件,△ABC与△A1B1C1相似的有( )
①A=450,AB=12,AC=15,A1=450,A1B1=16,A1C1=20
②AB=12,BC=15,AC=24, A1B1=20, A1C1=40,B1C1=25
③B=B1=750,C=500,A1=550
④C=C1=900,AB=10,AC=6,A1B1=15,A1C1=9
A.1个 B.2个 C.3个 D.4个
9.有同一三角形地块的甲乙两张地图,比例尺分别为1:100和1:500,那么甲地图与乙地图表示这一块的三角形面积比是 ( )
A.25 B.5 C.1:25 D.1:5
10.我们已经学习和掌握了不少在平地上测量建筑物高度的方法,如果在同一个斜坡上,在同一时刻,测得在斜坡上自己的影子和一幢大楼的影子长,那么由自己的身高( )
A.也能够求出楼高
B.还须知道斜坡的角度,才能求出楼高
C.不能求出楼高
D.只有在光线垂直于斜坡时,才能求出楼高
二、填空题
11.同一底片印出来的不同尺寸的照片也是________.
12.放大镜下的图形与原来的图形_____.
13.如果图形A与图形B相似,图形B与图形C相似,那么图形A与图形C____.
图形A 图形B 图形C
14.下列图形中是____与_____相似的.
(1) (2) (3) (4)
15.图中与三角形相似的有_________个.
16. 如果(x-y):y=1:2,那么x:y= .
17.两个相似三角形的周长之比为2:3,则它们的面积之比是 .
18.已知C是线段AB的黄金分割点,AC:AB0.618,则CB:AC= .
三、解答题
19.将下图分割成五个大小相等的图形.
20.请将一个任意三角形分成四个面积相等的三角形.
21.如图左边格点图中有一个四边形,请在右边的格点图中画出一个与该
四边形相似的图形,和你的伙伴交流一下,看看谁的方法又快又好.
22.如图,作线段将长方形分割同样大小的多边形.请将正方形作同样的分割.
23.下图中的两个多边形分别是幻灯片上的多边形ABCDEF和银幕上的多边形A1B1C1D1E1F1,它们的形状相同吗?
图4-14
在上图的两个多边形中,是否有相等的内角?设法验证你的猜测.
24.在方格纸中,△ABC与△DEF是否成位似图形?请说明你的理由.
25.试一试,把下列左边的图形放大到右边的格点图中.
26.请在格点图中任意画两个相似的图形.
A卷参考答案
一、1.D;形状相同
2. B;两个长方形不相似
3.B;关于形状相同,应该看成是没有一点不同之处.
4.B,两组
5.B
6.A;2:5=5:10
7. C;根据相似的定义
8. B;①④
9. C.1:25
10.A.能求出楼高
二、11. 相似图形
12. 相似
13. 相似;相似具有传递性
14.(1)(2)相似
15.4个
16.3:2
17.4:9
18. 0.618
三、19.图形如下
20.本题要求分成面积相等的三角形,因此可以利用“同底等高的三角形面积相等”这一性质来分割.
方法一:将某一边等分成四份,连结各分点与顶点(见左下图).
方法二:画出某一边的中线,然后将中线二等分,连结分点与另两个顶点(见右上图).
方法三:找出三条边上的中点,然后如左下图所示连结.
方法四:将三条边上的中点两两连结(见右上图).
前三种方法可以看成先将三角形分割成面积相等的两部分,然后分别将每部分再分割成面积相等的两部分.本题还有更多的分割方法.
21.本题答案不唯一
22.分割的图形如下
23.相似,对应的角相等.
24. △ABC与△DEF是相似图形,△ABC可以看作△DEF放大2倍后的图形
25.放大的图形如下
26.两个相似的三角形,答案不唯一
B等级
一.选择题
1.下列语句正确的是 ( )毛
A.在△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=30°,∠C′=60°, 则△ABC和△A′B′C′不相似
B.在△ABC和△A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,B′C′=14,A′B ′=10,则△ABC∽△A′B′C′
C.两个全等三角形不一定相似
D.所有的菱形都相似
2.如图所示,△ABC∽△ADE,AE=30cm,EC=15cm,BC=60cm,则DE的长为 ( )
A.40cm B.50cm C.45cm D.35cm
3.如图所示,能保证△ACD∽△ABC的条件是 ( )
A.AB:BC=AC:CD B.CD:AD=BC:AC
C.CD2=AD.DC D.AC2=AB.AD
4.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为 ( )
A.9:4 B.2:3 C.3:2 D.81:16
5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是 ( )
6.语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有 ( )
A.4句 B.3句 C.2句 D.1句
7.下列语句中不正确的是 ( )
A.求两条线段的比值,必需采用相同的长度单位
B.求两条线段的比值,只需采用相同的长度单位,与选用何种长度单位无关
C.两个相似三角形中,任意两组边对应成比例
D.不相似的两个三角形中,也有可能两组边对应成比例
8.下列各组图形有可能不相似的是 ( )
A.各有一个角是50°的两个等腰三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个等腰直角三角形
9.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,其最短边长为6,则最长边长为( )
A.12 B.18 C.24 D.30
10. 已知=k,则k=( )
A.2 B.-1 C.2或-1 D.0
二、填空题
11.如果一个三角形的面积扩大9倍,那么它的边长扩大_____________倍.
12.如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为______________.
13.如图所示的两个三角形是相似的x=_________,m=___________,n=____________.
14. 已知如图,两个矩形相似, 则x= ,y= ,α= .
15. 在相同时刻的物高与影长成比例,如果一古塔在地面上影长为50m,同时,高为1.5m的测竿的影长为2.5m,那么,古塔的高是___米.
16.如图中的两个矩形相似,则x=___________.
17. 请把下列各组图形是否相似的结论写在下面的括号里.
18.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是 .
三、解答题
19.把上下对应的相似图形用线连起来
20.如图所示,写出多边形ABCDEF各个顶点的坐标,并画出多边形ABCDEF 关于y轴的轴对称图形,它们相应的对称点的坐标有什么变化
21.学生会举办一个校园摄影艺术展览会,小华和小刚准备将矩形的作品四周镶上一圈等宽的纸边,如图所示.两人在设计时发生了争执:小华要使内外两个矩形相似,感到这样视觉效果较好;小刚试了几次不能办到,表示这是不可能的.小红和小莉了解情况后,小红说这一要求只有当矩形是黄金矩形时才能做到,小莉则坚持只有当矩形是正方形时才能做到.请你动手试一试,说一说你的看法.
22.以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:(1)都是直角三角形;(2)都是锐角三角形;(3)都是钝角三角形.
23.如果一个图形经过分割,能成为若干个与自身相似的图形,我们称它为“能相似分割的图形”,如图所示的等腰三角形和矩形就是能相似分割的图形.
(1)你能否再各举出一个 “能相似分割”的三角形和四边形?
(2)一般的三角形是否“能相似分割的图形”?如果是的话给出一种分割方案,否则说明原因.
24.我们通常用到的一种复印纸,整张称为A1纸,对折一分为二裁开成为A2纸,再一分为二成为A3纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位).
B卷参考答案
1.B;对应边成比例 2.A;根据对应边成比例 3.D;比例性质 4.C;相似形的性质 5.C;图形的相似 6.B;②③④ 7.C;注意对应 8.A;不符合对应关系 9. 由相似多边形对应边成比例,设最长边为x.
∴,∴2x=36,x=18.答案:B 10.C.2或-1
二、11.3倍 12.14m 13. 14.根据相似形的性质,得x=2.5,y=1.5,α=900;⑵x=22.5. 15.在相同时刻的物高与影长成比例,设古塔的高为xm,则,解得x=30(m) 16.已知两个矩形相似,根据相似形的性质,有,∴30x=15×20,解得x=10;又,∴x=22.5 17. ①相似,②不相似,③不相似,④相似,⑤不相似,⑥不相似 18. 由左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),不难发现左右眼睛之间的距离2个单位;平
移后的图形右图中左眼的坐标是(3,4),则右图案中右眼的坐标的纵坐标不变,横坐标为3+2=5,即右图案中右眼的坐标是(5,3).
三、19.相似形连线如(1)-(a),(2)-(d),(3)-(g)
20.提示:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3),A′(2,0),B′(0, 3),C′(-3,-3),D′(-4,0),E′(-3,3),F′(0,3).
21.只有正方形才能做到,设矩形的一边为a,另一边为b,等宽的纸边宽为c,按小华的要求,应有,化简得a=b.
22.作图如下
23.例如直角三角形,一组底角是60°、三边相等的等腰梯形. 三角形都是“能相似分割的图形”(提示:顺次连结三角形三边中点,将三角形分成的四个三角形都和原三角形相似)
24. 1.414(提示:设 A1纸的长为a,观为b ,由A1,A2纸的长余观对应成比例,得a:b=b:a)
C等级
一、选择题
1.两个相似五边形,一组对应边的长分别为3cm和4.5cm,则这两个多边形的相似比可能是( )
(A) (B) (C) (D)
2.有同一三角形地块的甲、乙两地图,比例尺分别为1:100和1:500,那么甲地图与乙地图表示这一地块的三角形的相似比是( )
(A)5:1 (B)25:1 (C)1:25 (D)1:5
3.在一张由复印机复印出来的纸上,一个多边形的一条边由原来的1cm变成了4cm,那么这个多边形的另一条边由原来4cm变成了( ).
(A)4cm (B)8cm (C)16cm (D)32cm
4. 下列成比例的一组线段是( )
(A)a=2,b=4,c=6,d=8 (B)a=3,b=4,c=9,d=12
(C)a=2,b=6,c=8,d=9 (D)a=6,b=9,c=10,d=12
5. 下列说法:①相似多边形一定全等;②不相似多边形一定不全等;③全等多边形不一定相似;④全等多边形一定相似.其中正确的是( )
(A)①② (B)②③ (C)②④ (D)③④
6. 小明同学在学习相似形后,总结了能够形似的图形,下面是他给出的几个图形中一定能相似的是( )
(A)两个矩形(B)两个平行四边形 (C)两个正四边形 (D)两个菱形
二、填空题
7.已知A、B两地相距300km,在地图上量得两地相距15cm,则图上距离与实际距离之比为______.
8.用100倍的放大镜看一个正方形,则所看到正方形与原正方形的形状关系是____.
9.已知正方形ABCD与正方形DEFG的边长分别是2cm和4cm,则正方形ABCD与正方形DEFG的相似比是___.
10.已知矩形ABCD∽矩形EFGH,若AB=5cm,BC=6cm,EF=10cm,则FG=_____.
三、解答题
11.请你说清楚所有的正方形都相似的道理
12.我们已经学习了相似多边形,也知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长,对角线等所有元素都对应成比例,就可以称它们为相似图形.
现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形.请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.
13.如图1,两个梯形相似.
(1)求α的度数;(2)求x和y的值.
( http: / / www.21cnjy.com / )
图1
14.已知四边形ABCD与四边形A′B′C′D′相似,且AB:BC:CD:DA=20:15:9:8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
答案:
一、1.D 2.A 3.C 4.B 5.C 6.C
二、7.1:2 000 000;8.相似; 9.; 10.12cm
三、11.∵正方形每个内角都等于90°,∴所有的正方形的对应角相等.∵正方形每条边都相等,∴所有的正方形的对应边的比都相等.即:所有的正方形的各角对应相等,各边对应成比例,因此所有正方形都相似.
12.1. ①、④是相似图形,②、③不一定是相似图形 理由:两个圆和两个正六边形分别为形似图形,因为它们的对应元素都成比例;两个菱形和两个长方形都不是,因为它们的对应元素不一定都成比例(或举出具体的反例).
13.(1)根据相似多边形的对应边角相等可得α=45°,(2)根据相似多边形的对应边成比例可得x=HYPERLINK "http://www.21cnjy.com/" EMBED Equation.3 ,y=.
14.因为四边形ABCD与四边形A′B′C′D′相似,且AB:BC:CD:DA=20:15:9:8,
所以A′B′:B′C′:C′D′:D′A′=20:15:9:8
设A′B′=20x,B′C′=15x,C′D′=9x,D′A′=8x,由四边形A′B′C′D′的周长为26,得20x+15x+9x+8x=26,解得x=
所以A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4
A
E
D
C
B
图1
图4
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
D
E
F
B
C
A
A
C
A
B
C
B
1250
800
╯
╮
650
╭
α
╰
╯
800
3
-3
-2
-1
3
2
1
O
-1
-2
1
2
3
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二十六章二次函数
第19课时 §27.1 图形的相似
同学们在上册已经学习了图形的全等,与全等图形相比,形状相同的图形不仅是现实世界运动变化的最简捷形式之一,而且是现实生活中更为广泛存在的现象(全等图形其实就是它的一个特例).现实世界中既有图形的全等变换,也有图形的相似变换,事实上,探索相似图形的一些重要性质,不仅是认识、描述物体的形状,更好地刻画现实世界的必要手段,而且也是解决现实世界中的具体问题,进行数学交流的重要工具.
本章是继“图形全等、三角形全等”之后集中研究图形形状的内容,不仅是对图形全等内容的进一步深化和发展,而且是对图形研究方法的综合运用.学习本章有关内容,不仅是第三学段“图形的认识”、“图形与变换”等部分的重要目标,而且也是密切数学与现实之间必然联系以及“图形与空间”各部分之间内在联系的重要桥梁.因此,学好本章的内容十分重要.我们来看下面的问题:
1.小颖测得2m高的标杆在太阳下的影长为1.2m,同时又
测得一棵树的影长为3.6m,请你帮助小颖计算出这棵树的高度.
2.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,
某一时刻AB在阳光下的投影BC=3m.
(1)请你在图4.1中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光
下的投影长为6m,请你计算DE的长
相信,通过本章的学习,上述问题是不难解决的.
点击一:线段的比的定义
(1)线段比的概念:在同一单位下,两条线段长度的比.叫做这两条线段的比.
(2)比例线段的定义:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段.简称比例线段,如四条线段a,b,c,d,有,那么这四条线段叫做成比例线段.
(3)比例尺:在地图或者工程图纸上,图上长度与实际长度的比通常叫做比例尺.如你照的全身照片与你本人相比,缩小了很多,若用1:20表示,则把比例尺称为1:20.
(4)比例的基本性质:如果,那么ad=bc(a,b,c,d都不为零).特例:若,那么b2=ac,则把b叫做a,c的比例中项.
(5)比例性质的推广:
针对练习1:
1. 如图2,直线CD∥EF,若OC=3,CE=4,则的值是( )
A. B. C. D.
答案:C
2. 已知A、B两地的实际距离是5km,画在图上的距离为2cm,则该地图的比例尺为
A.2:5 B.1:2500 C.250000:1 D. 1:250000
答案:D
点击二:相似形的概念
(1)定义:一般地说:形状相同的两个图形称为相似图形.从所学习的多边形而言:对应角相等,对应边成比例的两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
(2)相似多边形写法:用符号“∽”表示,读作“相似于”.
相似形定义应注意两点:(1)相同点:形状相同;(2)不同点:大小不一定相同.
点击三:相似形的识别
形状相同识识别图形相似的重要标致.
通过生活中的实例认识物体和图形的相似;感受形状相同是识别图形相似的重要标致.理解相似图形概念;会判断两个图形是否相似.
相似形与全等形的联系与区别:全等形是相似形的特殊情况.全等一定相似,但相似不一定全等.
点击四: 相似形的性质
相似形的对应边相等,对应角相等.
点击五:相似多边形的性质
相似多边形的对应边成比例,对应角相等;反之,如果两个多边形的对应角相等,对应边成比例,那么这两个多边形相似.两个边数不同的多边形一定不相似,仅有对应角相等(如正方形与矩形)或仅有对应边成比例(如正方形与菱形)的多边形并不一定相似.
针对练习:
1.如图1,点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是( ).
A. B. C. D.
答案:A
2.在下列四组图形中,不相似的有 ( )
A.1组 B.2组 C.3组 D.4组
答:B
3.若如图4所示的两个四边形相似,则的度数是( ).
A. B. C. D.
答:A
4.将一个矩形纸片ABCD沿AD和BC的中点的连线对折,要使矩形AEFB与原矩形相似,
则原矩形的长和宽的比应为( ).
A.2:1 B. C. D.1:1
答:C
类型之一:图形相似和相似图形的概念
例1: 下面是两张大小不同的中国地图,左边的图形与右边的图形有怎样的关系?
【解析】左边的中国地图图形可以看作是右边的中国地图图形缩小得来的.由于不同的需要,经常会制成各种大小的中国地图地图,但其形状(包括地图中所描绘的各个部分)肯定是相同的.
答案:这两幅地图相似.
例2: 图中有哪些图形是相似图形?
【解析】 根据图形的形状相同的特点知:(1)与(3),(2)与(13),(4)与(11),(5)与(10),(14)与(16),(6)、(7)、(8)与(9)分别相似.
例3: 找一找:下列图形哪些形状相同?用线连起来.
【解析】 形状相同的图形即为相似形,用线连接如下.
本题中的两两相似的图形分别有:两朵红花、两朵绿花、两个三角形和两个猫,它们的形状相同,只是大写不同.符合相似形的特征.
例4 把四边形ABCD放大1倍(要求:放大后的顶点在格点上).
【解析】 把四边形ABCD放大1倍,如下图所示:
图形成倍的放大或缩小,其大下发生了改变,但形状不变,即放大或缩小后的两个图形形状相同.这样的两个图形是相似图形.
类型之二:相似多边形的性质
例3:如图1,已知四边形ABCD与四边形A′B′C′D′相似,求BC、CD的长和∠D′的大小.
解:因为四边形ABCD与四边形A′B′C′D′相似,
故它们的对应边成比例,对应角相等.
所以.
解之,得BC=54,CD=45.
又因为∠C′=∠C=82°,
所以∠D′=360°-(70°+120°+82°)=88°.
例4:如图2所示,这两个菱形相似吗?请说明你的理由.
解:这两个菱形不相似.因为这两个菱形的对应角不相等,第一个菱形的内角分别为45°,135°,45°,135°,而第二个菱形的内角分别为60°,120°,60°,120°,它们仅对应边成比例.
例5: 已知图3中的两个梯形相似,求未知边x、y、z的长度和∠α、∠β的度数.
分析:解题时要充分利用相似多边形的特征和梯形的性质.
解:因为两个梯形相似,
所以.
解之,得x=3,y=6,z=3.
又因为对应角相等,
所以∠α=∠D=180°-∠A=180°-62°=118°,
∠β=∠B′=180°-∠C′=180°-110°=70°.
一.选择题
1.下列各线段的长度成比例的是( )毛
A.2cm,5cm,6cm,8cm B.1cm,2cm,3cm,4cm
C.3cm,6cm,7cm,9cm D.3cm,6cm,9cm,18cm
2.已知A,B两地的实际距离是250米,若画在图上的距离是5厘米, 则图上距离与实际距离的比是( )
A.1:50 B.1:5000 C.1:500 D.1:50000
3.下列语句中不正确的是( ).
(A)求两条线段的比值,必需采用相同的长度单位
(B)求两条线段的比值,只需采用相同的长度单位,与选用何种长度单位无关
(C)两个相似三角形中,任意两组边对应成比例
(D)不相似的两个三角形中,也有可能两组边对应成比例
4.下列各组图形有可能不相似的是( ).
(A)各有一个角是50°的两个等腰三角形;(B)各有一个角是100°的两个等腰三角形
(C)各有一个角是50°的两个直角三角形;(D)两个等腰直角三角形
5.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面( )
(A)2.4米 (B)2.8米 (C)3米 (D)高度不能确定
6.下列语句正确的是( )毛
A.在△ABC和△A′B′C′中,∠B=∠B′=90°, ∠A=30°,
∠C′=60°, 则△ABC和△A′B′C′不相似;
B.在△ABC和△A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,
B′C′=14,A′B ′=10,则△ABC∽△A′B′C′;
C.两个全等三角形不一定相似; D.所有的菱形都相似
7.如图所示, △ABC∽△ADE,AE=30cm,EC=15cm,BC=60cm,则DE的长为( )
A.40cm B.50cm C.45cm D.35cm
8.如图所示,能保证△ACD∽△ABC的条件是( )
A.AB:BC=AC:CD B.CD:AD=BC:AC
C.CD2=AD.DC D.AC2=AB.AD
9.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为( )
A.9:4 B.2:3 C.3:2 D.81:16
10.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是( )
11.等边三角形的一条中线与一条中位线长的比是( )
A. :1; B.:2; C.:; D.1:3
12.如图所示,在□ABCD中,BE交AC,CD于G,F,交AD的延长线于E, 则图中的相似三角形有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
1.已知:.(1)当a=1时,b=___,c=____;(2)当a≠0时 ,=_______.
2.两个相似三角形的一组对应边长分别为15和27,它们的周长之差为36,则较小三角形的周长是 .
3.若一个边长为10cm的等边三角形ABC内接一个正方形DEFG,且点D,E在BC边上,点F,G分别在AC,AB边上,则正方形DEFG的边长是_____.
4.如果一个三角形的面积根据相似的知识扩大9倍,那么它的周长扩大________倍.
5.如图所示, △ABC中,DE∥FG∥BC,且AD=DF=FB,则
S△AFG:S△ABC=_______.
6.在矩形ABCD中,AB=3BC,P为DC上任意一点,使得
△ADP与△PBC相似的点P有________个.
三、解答题
1.任意画一个三角形,再把它放大到原来的3倍.
2.如图所示,铁道口的栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米时, 长臂端点升高了几米
3.将矩形纸片ABCD沿折痕EF对折,使点A与C重合.若已知AB=6cm,BC=8cm,求EF的长.
4.已知:正方形的边长为1.
(1)如图(1)所示,可以算出一个正方形的对角线长为 , 那么两个正方形并排拼成的矩形的对角线的长呢 n个正方形并排拼成的矩形的对角线长呢
(2)根据图(2),说明△BCE∽△BED;
(3)由图(3),在下列所给的3个结论中, 通过合理推理选出一个正确的结论加以说明.
(A)∠BEC+∠BDE=45°; (B)∠BEC+∠BED=45°; (C)∠BEC+∠DFE=45°.
5.如图所示,已知凸透镜焦距 =10cm,一根点燃的蜡烛放在距凸透镜15cm的主光轴上,现测得烛焰AB长为2cm,通过调节光屏位置,得到烛焰在光屏上清晰的像.
(1)请根据凸透镜成像原理(与主光轴平行的光线经过凸透镜折射后,通过凸透镜的焦点,经过凸透镜光心的光线不改变方向),画出烛焰的像的位置;
(2)求出烛焰像的长度.
6.如图所示,有一条路CF为15米宽,这条路的北侧有一栋11层高的楼AB, 为33米的高层住宅,这条路的南侧有一栋电力公司办公楼CD,为12米高, 已知高层住宅的每层楼都一样高,当某一时刻,高层住宅楼的影长是165米,办公楼的影子映在住宅楼上,使下面的几层没有见到阳光,请你通过计算说明此刻高层住宅从第几层开始没有被前面的办公楼档住阳光.
答案:
一、DBCAA BADCB AD
二、1.2,3,3 2.45 3.(20-30)CM; 4.3 5.4:9 6.3
三、1.略 2.8米 3.15/2 (先求得OC=5,再由△COE∽△CBA求得OE=5/4)
4.(1), (2)解:由BE=,BC=1,BD=2,
∴, 且∠EBD=135°,
∴△BCE∽△BED.
(3)解:由(2)知,△BCE∽∽BED,有∠BEC=∠BED, ∠BCE=∠BED,
又∠BEC+∠BCE=45°,∴∠BEC+∠BED=45°,
所以(B)成立.
HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4
∴△BEC∽△DEF,∴∠BCE=∠DFE,
又∠BEC+ ∠BCE=45°,∴∠BEC+∠DFE=45°,所以(C)成立.
5. (1)略, (2)4cm; 24.略.毛
6.解:过E作EM⊥CD于M,设EF=x,则DM=12-x.
由题意知:,∴x=9.
又33 米高的楼是11层,
∴1层楼为3米高,因此EF是3层楼高.
∴从第4 层开始没有被前面的办公楼挡住阳光.
一、认认真真,书写快乐
1.两个相似图形的 相同, 不一定相同.
2.放大镜下看到的物体图形与原来的图形 相似图形(填“是”或“不是”)
3.在中国地理地图册上,连接上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图1所示.飞机从台湾直飞上海的距离为1 286千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是 千米.
4.科学研究表明,当人的下肢长与身高之比为0.618时,看起来最美.某成年女士身高为155cm,下肢长94cm,按此比例,该女士穿的高跟鞋鞋跟的最佳高度应约为 cm(精确到0.1)
5.在比例尺为1∶m的地图上,某市为长5cm,宽为2cm的矩形地域,则该市的实际地域面积为 平方米.
二、仔仔细细,记录自信
6.下面每组图中的两个图形是相似图形的是( )
7.下面每组图中的两个图形不是相似图形的是( )
8.下列说法错误的是( )
A.同一底片冲洗出的一张一寸照片和一张两寸照片相似
B.大小不一的两张中国地图相似
C.一个人在哈哈镜中的形象与他本人是相似的
D.国旗上的大小五角星相似
9.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB之比为( )
A.3∶4 B.2∶3 C.3∶5 D.1∶2
10.应中共中央总书记胡锦涛同志的邀请,中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的“大唐芙蓉园”.该园占地面积约为800 000m2,若按比例尺1∶2 000缩小后,其面积大约相当于( )
A.一个篮球场的面积
B.一张乒乓球台台面的面积
C.《人民日报》的一个版面的面积
D.《数学》课本封面的面积
三、平心静气,展示智慧
11.一块长3m,宽1.5m的矩形黑板如图2所示,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?
12.我们已经学习了相似三角形,也知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.
现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.
参考答案:
一、1.形状,大小 2.是 3.3 858 4.4.7 5.
二、6.B 7.D 8.C 9.A 10.C
三、11.答:不相似,因为对应边不成比例.
12.圆和正六边形是相似图形,因为它们的形状相同;菱形和长方形不是相似图形,因为它们的形状不一定相同.
1.如图,在正方形网格中,每个小正方形的边长均为1个单位.将向下平移4个单位,得到,再把绕点顺时针旋转,得到,请你画出和(不要求写画法).
【解析】 先将向下平移4个单位,得到,再把绕点顺时针旋转,得到,结果如图所示:
本题融图形的平移、旋转于一体,综合性、操作性强,主要考查学生实际动手操作能力.由于平移、旋转不改变图形的大小,故平移、旋转后的三角形与原三角形的关系全等,是属于相似的特例.
2.如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点D顺时针方向旋转900,1800,2700的图案,
你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为l,旋转后点A的对应点依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.
【解析】 (1)如图,正确画出图案
(2)如图,=-4
=(3+5)2-4××3×5
=34
故四边形似AA1A2A3的面积为34.
(3)结论:AB2+BC2=AC2或勾股定理的文字叙述
课时作业:
A等级
一、选择题
1.下面图形中,相似的一组是( )
A B C D
2.下面给出的图形中,不是相似的图形的是( )
A.刚买的一双手套的左右两只 B.仅仅宽度不同的两快长方形木板
C.一对羽毛球球拍 D.复印出来的两个“春”字
3. 在下列四组图形中,不相似的有( )
A.1组 B.2组 C.3组 D.4组
4. 如图,下列四组图形中,两个图形不相似的有( )
A.1组 B.2组 C.3组 D.4组
5.你看到过哈哈镜吗?哈哈镜中的形象与你本人相似的识( )
A B C D
6.a、b、c、d是四条线段,下列各组中这四条线段成比例的是 ( )
A.a=2cm, b=5cm, c=5cm, d=10cm
B.a=5cm, b=3cm, c=5cm, d=3cm
C.a=30cm, b=2cm, c=0.8cm, d=2cm
D.a=5cm, b=0.02cm, c=7cm, d=0.3cm
7.下列图形中一定相似的一组是 ( )
A.邻边对应成比例的两个平行四边形 B.有一条边相等的两个矩形
C.有一个内角相等的两个菱形 D.底角都是600的两个等腰三角形
8.根据下列各组条件,△ABC与△A1B1C1相似的有( )
①A=450,AB=12,AC=15,A1=450,A1B1=16,A1C1=20
②AB=12,BC=15,AC=24, A1B1=20, A1C1=40,B1C1=25
③B=B1=750,C=500,A1=550
④C=C1=900,AB=10,AC=6,A1B1=15,A1C1=9
A.1个 B.2个 C.3个 D.4个
9.有同一三角形地块的甲乙两张地图,比例尺分别为1:100和1:500,那么甲地图与乙地图表示这一块的三角形面积比是 ( )
A.25 B.5 C.1:25 D.1:5
10.我们已经学习和掌握了不少在平地上测量建筑物高度的方法,如果在同一个斜坡上,在同一时刻,测得在斜坡上自己的影子和一幢大楼的影子长,那么由自己的身高( )
A.也能够求出楼高
B.还须知道斜坡的角度,才能求出楼高
C.不能求出楼高
D.只有在光线垂直于斜坡时,才能求出楼高
二、填空题
11.同一底片印出来的不同尺寸的照片也是________.
12.放大镜下的图形与原来的图形_____.
13.如果图形A与图形B相似,图形B与图形C相似,那么图形A与图形C____.
图形A 图形B 图形C
14.下列图形中是____与_____相似的.
(1) (2) (3) (4)
15.图中与三角形相似的有_________个.
16. 如果(x-y):y=1:2,那么x:y= .
17.两个相似三角形的周长之比为2:3,则它们的面积之比是 .
18.已知C是线段AB的黄金分割点,AC:AB0.618,则CB:AC= .
三、解答题
19.将下图分割成五个大小相等的图形.
20.请将一个任意三角形分成四个面积相等的三角形.
21.如图左边格点图中有一个四边形,请在右边的格点图中画出一个与该
四边形相似的图形,和你的伙伴交流一下,看看谁的方法又快又好.
22.如图,作线段将长方形分割同样大小的多边形.请将正方形作同样的分割.
23.下图中的两个多边形分别是幻灯片上的多边形ABCDEF和银幕上的多边形A1B1C1D1E1F1,它们的形状相同吗?
图4-14
在上图的两个多边形中,是否有相等的内角?设法验证你的猜测.
24.在方格纸中,△ABC与△DEF是否成位似图形?请说明你的理由.
25.试一试,把下列左边的图形放大到右边的格点图中.
26.请在格点图中任意画两个相似的图形.
A卷参考答案
一、1.D;形状相同
2. B;两个长方形不相似
3.B;关于形状相同,应该看成是没有一点不同之处.
4.B,两组
5.B
6.A;2:5=5:10
7. C;根据相似的定义
8. B;①④
9. C.1:25
10.A.能求出楼高
二、11. 相似图形
12. 相似
13. 相似;相似具有传递性
14.(1)(2)相似
15.4个
16.3:2
17.4:9
18. 0.618
三、19.图形如下
20.本题要求分成面积相等的三角形,因此可以利用“同底等高的三角形面积相等”这一性质来分割.
方法一:将某一边等分成四份,连结各分点与顶点(见左下图).
方法二:画出某一边的中线,然后将中线二等分,连结分点与另两个顶点(见右上图).
方法三:找出三条边上的中点,然后如左下图所示连结.
方法四:将三条边上的中点两两连结(见右上图).
前三种方法可以看成先将三角形分割成面积相等的两部分,然后分别将每部分再分割成面积相等的两部分.本题还有更多的分割方法.
21.本题答案不唯一
22.分割的图形如下
23.相似,对应的角相等.
24. △ABC与△DEF是相似图形,△ABC可以看作△DEF放大2倍后的图形
25.放大的图形如下
26.两个相似的三角形,答案不唯一
B等级
一.选择题
1.下列语句正确的是 ( )毛
A.在△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=30°,∠C′=60°, 则△ABC和△A′B′C′不相似
B.在△ABC和△A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,B′C′=14,A′B ′=10,则△ABC∽△A′B′C′
C.两个全等三角形不一定相似
D.所有的菱形都相似
2.如图所示,△ABC∽△ADE,AE=30cm,EC=15cm,BC=60cm,则DE的长为 ( )
A.40cm B.50cm C.45cm D.35cm
3.如图所示,能保证△ACD∽△ABC的条件是 ( )
A.AB:BC=AC:CD B.CD:AD=BC:AC
C.CD2=AD.DC D.AC2=AB.AD
4.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为 ( )
A.9:4 B.2:3 C.3:2 D.81:16
5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是 ( )
6.语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有 ( )
A.4句 B.3句 C.2句 D.1句
7.下列语句中不正确的是 ( )
A.求两条线段的比值,必需采用相同的长度单位
B.求两条线段的比值,只需采用相同的长度单位,与选用何种长度单位无关
C.两个相似三角形中,任意两组边对应成比例
D.不相似的两个三角形中,也有可能两组边对应成比例
8.下列各组图形有可能不相似的是 ( )
A.各有一个角是50°的两个等腰三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个等腰直角三角形
9.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,其最短边长为6,则最长边长为( )
A.12 B.18 C.24 D.30
10. 已知=k,则k=( )
A.2 B.-1 C.2或-1 D.0
二、填空题
11.如果一个三角形的面积扩大9倍,那么它的边长扩大_____________倍.
12.如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为______________.
13.如图所示的两个三角形是相似的x=_________,m=___________,n=____________.
14. 已知如图,两个矩形相似, 则x= ,y= ,α= .
15. 在相同时刻的物高与影长成比例,如果一古塔在地面上影长为50m,同时,高为1.5m的测竿的影长为2.5m,那么,古塔的高是___米.
16.如图中的两个矩形相似,则x=___________.
17. 请把下列各组图形是否相似的结论写在下面的括号里.
18.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是 .
三、解答题
19.把上下对应的相似图形用线连起来
20.如图所示,写出多边形ABCDEF各个顶点的坐标,并画出多边形ABCDEF 关于y轴的轴对称图形,它们相应的对称点的坐标有什么变化
21.学生会举办一个校园摄影艺术展览会,小华和小刚准备将矩形的作品四周镶上一圈等宽的纸边,如图所示.两人在设计时发生了争执:小华要使内外两个矩形相似,感到这样视觉效果较好;小刚试了几次不能办到,表示这是不可能的.小红和小莉了解情况后,小红说这一要求只有当矩形是黄金矩形时才能做到,小莉则坚持只有当矩形是正方形时才能做到.请你动手试一试,说一说你的看法.
22.以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:(1)都是直角三角形;(2)都是锐角三角形;(3)都是钝角三角形.
23.如果一个图形经过分割,能成为若干个与自身相似的图形,我们称它为“能相似分割的图形”,如图所示的等腰三角形和矩形就是能相似分割的图形.
(1)你能否再各举出一个 “能相似分割”的三角形和四边形?
(2)一般的三角形是否“能相似分割的图形”?如果是的话给出一种分割方案,否则说明原因.
24.我们通常用到的一种复印纸,整张称为A1纸,对折一分为二裁开成为A2纸,再一分为二成为A3纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位).
B卷参考答案
1.B;对应边成比例 2.A;根据对应边成比例 3.D;比例性质 4.C;相似形的性质 5.C;图形的相似 6.B;②③④ 7.C;注意对应 8.A;不符合对应关系 9. 由相似多边形对应边成比例,设最长边为x.
∴,∴2x=36,x=18.答案:B 10.C.2或-1
二、11.3倍 12.14m 13. 14.根据相似形的性质,得x=2.5,y=1.5,α=900;⑵x=22.5. 15.在相同时刻的物高与影长成比例,设古塔的高为xm,则,解得x=30(m) 16.已知两个矩形相似,根据相似形的性质,有,∴30x=15×20,解得x=10;又,∴x=22.5 17. ①相似,②不相似,③不相似,④相似,⑤不相似,⑥不相似 18. 由左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),不难发现左右眼睛之间的距离2个单位;平
移后的图形右图中左眼的坐标是(3,4),则右图案中右眼的坐标的纵坐标不变,横坐标为3+2=5,即右图案中右眼的坐标是(5,3).
三、19.相似形连线如(1)-(a),(2)-(d),(3)-(g)
20.提示:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3),A′(2,0),B′(0, 3),C′(-3,-3),D′(-4,0),E′(-3,3),F′(0,3).
21.只有正方形才能做到,设矩形的一边为a,另一边为b,等宽的纸边宽为c,按小华的要求,应有,化简得a=b.
22.作图如下
23.例如直角三角形,一组底角是60°、三边相等的等腰梯形. 三角形都是“能相似分割的图形”(提示:顺次连结三角形三边中点,将三角形分成的四个三角形都和原三角形相似)
24. 1.414(提示:设 A1纸的长为a,观为b ,由A1,A2纸的长余观对应成比例,得a:b=b:a)
C等级
一、选择题
1.两个相似五边形,一组对应边的长分别为3cm和4.5cm,则这两个多边形的相似比可能是( )
(A) (B) (C) (D)
2.有同一三角形地块的甲、乙两地图,比例尺分别为1:100和1:500,那么甲地图与乙地图表示这一地块的三角形的相似比是( )
(A)5:1 (B)25:1 (C)1:25 (D)1:5
3.在一张由复印机复印出来的纸上,一个多边形的一条边由原来的1cm变成了4cm,那么这个多边形的另一条边由原来4cm变成了( ).
(A)4cm (B)8cm (C)16cm (D)32cm
4. 下列成比例的一组线段是( )
(A)a=2,b=4,c=6,d=8 (B)a=3,b=4,c=9,d=12
(C)a=2,b=6,c=8,d=9 (D)a=6,b=9,c=10,d=12
5. 下列说法:①相似多边形一定全等;②不相似多边形一定不全等;③全等多边形不一定相似;④全等多边形一定相似.其中正确的是( )
(A)①② (B)②③ (C)②④ (D)③④
6. 小明同学在学习相似形后,总结了能够形似的图形,下面是他给出的几个图形中一定能相似的是( )
(A)两个矩形(B)两个平行四边形 (C)两个正四边形 (D)两个菱形
二、填空题
7.已知A、B两地相距300km,在地图上量得两地相距15cm,则图上距离与实际距离之比为______.
8.用100倍的放大镜看一个正方形,则所看到正方形与原正方形的形状关系是____.
9.已知正方形ABCD与正方形DEFG的边长分别是2cm和4cm,则正方形ABCD与正方形DEFG的相似比是___.
10.已知矩形ABCD∽矩形EFGH,若AB=5cm,BC=6cm,EF=10cm,则FG=_____.
三、解答题
11.请你说清楚所有的正方形都相似的道理
12.我们已经学习了相似多边形,也知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长,对角线等所有元素都对应成比例,就可以称它们为相似图形.
现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形.请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.
13.如图1,两个梯形相似.
(1)求α的度数;(2)求x和y的值.
( http: / / www.21cnjy.com / )
图1
14.已知四边形ABCD与四边形A′B′C′D′相似,且AB:BC:CD:DA=20:15:9:8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
答案:
一、1.D 2.A 3.C 4.B 5.C 6.C
二、7.1:2 000 000;8.相似; 9.; 10.12cm
三、11.∵正方形每个内角都等于90°,∴所有的正方形的对应角相等.∵正方形每条边都相等,∴所有的正方形的对应边的比都相等.即:所有的正方形的各角对应相等,各边对应成比例,因此所有正方形都相似.
12.1. ①、④是相似图形,②、③不一定是相似图形 理由:两个圆和两个正六边形分别为形似图形,因为它们的对应元素都成比例;两个菱形和两个长方形都不是,因为它们的对应元素不一定都成比例(或举出具体的反例).
13.(1)根据相似多边形的对应边角相等可得α=45°,(2)根据相似多边形的对应边成比例可得x=HYPERLINK "http://www.21cnjy.com/" EMBED Equation.3 ,y=.
14.因为四边形ABCD与四边形A′B′C′D′相似,且AB:BC:CD:DA=20:15:9:8,
所以A′B′:B′C′:C′D′:D′A′=20:15:9:8
设A′B′=20x,B′C′=15x,C′D′=9x,D′A′=8x,由四边形A′B′C′D′的周长为26,得20x+15x+9x+8x=26,解得x=
所以A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4
A
E
D
C
B
图1
图4
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
D
E
F
B
C
A
A
C
A
B
C
B
1250
800
╯
╮
650
╭
α
╰
╯
800
3
-3
-2
-1
3
2
1
O
-1
-2
1
2
3
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
