28.1锐角三角函数
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二十六章二次函数
第22课时 §28.1 锐角三角函数
本章“锐角三角函数”属于三角形,是《数学课程标准》中“空间与图形”领域的重要内容。从《数学课程标准》看,中学数学把三角形内容分成两个部分,第一部分放在义务教育阶段,第二部分放在高中阶段。在义务教育阶段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
本章包括锐角三角函数的概念(主要是正弦、余弦和正切的概念),以及利用锐角三角函数解直角三角形等内容。锐角三角函数为解直角三角形提供了有效的工具,解直角三角形在实际当中有着广泛的应用,这也为锐角三角函数提供了与实际联系的机会。研究锐角三角函数的直接基础是相似三角形的一些结论,解直角三角形主要依赖锐角三角函数和勾股定理等内容,因此相似三角形和勾股定理等是学习本章的直接基础。本章重点是锐角三角函数的概念和直角三角形的解法。锐角三角函数的概念既是本章的难点,也是学习本章的关键。难点在于,锐角三角函数的概念反映了角度与数值之间对应的函数关系,这种角与数之间的对应关系,以及用含有几个字母的符号sinA、cosA、tanA表示函数等,学生过去没有接触过,因此对学生来讲有一定的难度。至于关键,因为只有正确掌握了锐角三角函数的概念,才能真正理解直角三角形中边、角之间的关系,从而才能利用这些关系解直角三角形。
在余弦函数和正切函数的概念给出之后,教科书在边注中分析了锐角三角函数的角与数值之间的对应关系,突出了函数的思想。一些特殊角的三角函数值是经常用到的,教科书借助于学生熟悉的两种三角尺研究了、、角的正弦、余弦和正切值,并以例题的形式介绍了已知锐角三角函数值求锐角的问题,当然这时所要求出的角都是、和的特殊角。教科书把求特殊角的三角函数值和已知特殊角的三角函数值求角这两个相反方向的问题安排在一起,目的是体现锐角三角函数中角与函数值之间的对应关系。本节最后,教科书介绍了如何使用计算器求非特殊角的三角函数值以及如何根据三角函数值求对应的角等内容。由于不同的计算器操作步骤有所不同,教科书只就常见的情况进行介绍。
在第28.1节 “锐角三角函数”中,教科书先研究了正弦函数,然后在正弦函数的基础上给出余弦函数和正切函数的概念。在第28.1节 “锐角三角函数”中,教科书先研究了正弦函数,然后在正弦函数的基础上给出余弦函数和正切函数的概念。在余弦函数和正切函数的概念给出之后,教科书在边注中分析了锐角三角函数的角与数值之间的对应关系,突出了函数的思想。一些特殊角的三角函数值是经常用到的,教科书借助于学生熟悉的两种三角尺研究了、、角的正弦、余弦和正切值,并以例题的形式介绍了已知锐角三角函数值求锐角的问题,当然这时所要求出的角都是、和的特殊角。教科书把求特殊角的三角函数值和已知特殊角的三角函数值求角这两个相反方向的问题安排在一起,目的是体现锐角三角函数中角与函数值之间的对应关系。
点击一:锐角三角函数定义
如图1,在Rt△ABC中,如果锐角A确定,那么
∠A的对边与斜边的比叫做∠A的正弦,记作sinA ,即sinA=;
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=;
∠A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA=.
锐角A的正弦、余弦和正切都是∠A的三角函数.
注意:(1)由于锐角三角函数是一种比值,因此它只有大小而没有单位;
(2)由于三角函数是一个比值,它的大小仅与角的大小有关,而与它所在的三角形的边的长度无关;
(3)sinA、cosA、tanA是一些完整的符号,不能把sinA看作sin与A的积,离开了A的sin没有任何意义,只有合起来,sinA才表示∠A的正弦. cosA、tanA也是如此.
针对练习1:
1.正方形网格中,如图放置,则的值为( )
A. B.HYPERLINK "http://www.21cnjy.com/"EMBED Unknown C. D.2
答案:A
2.正方形网格中,如图放置,则=( )
A. B.
C. D.
答案:B
3.在中,,若,则的值是( )
A. B.2 C. D.
答案:A
4.在Rt△ABC 中, ∠C=90,AB=4,AC=1,则的值是 ( )
A. B. C. D.4
答案:B
5.在正方形网格中,的位置如图所示,则的值为( )
A. B. C. D.
答案:B
6.如图,已知⊙O的半径为1,AB与⊙O相切于点A,OB与⊙O交于点C,CD⊥OA,垂足为D,则cos ∠AOB的值等于( )
A.OD B.OA C.CD D.AB
答案:A
7.已知中,AC=4,BC=3,AB=5,则( )
A. B. C. D.
答案:A
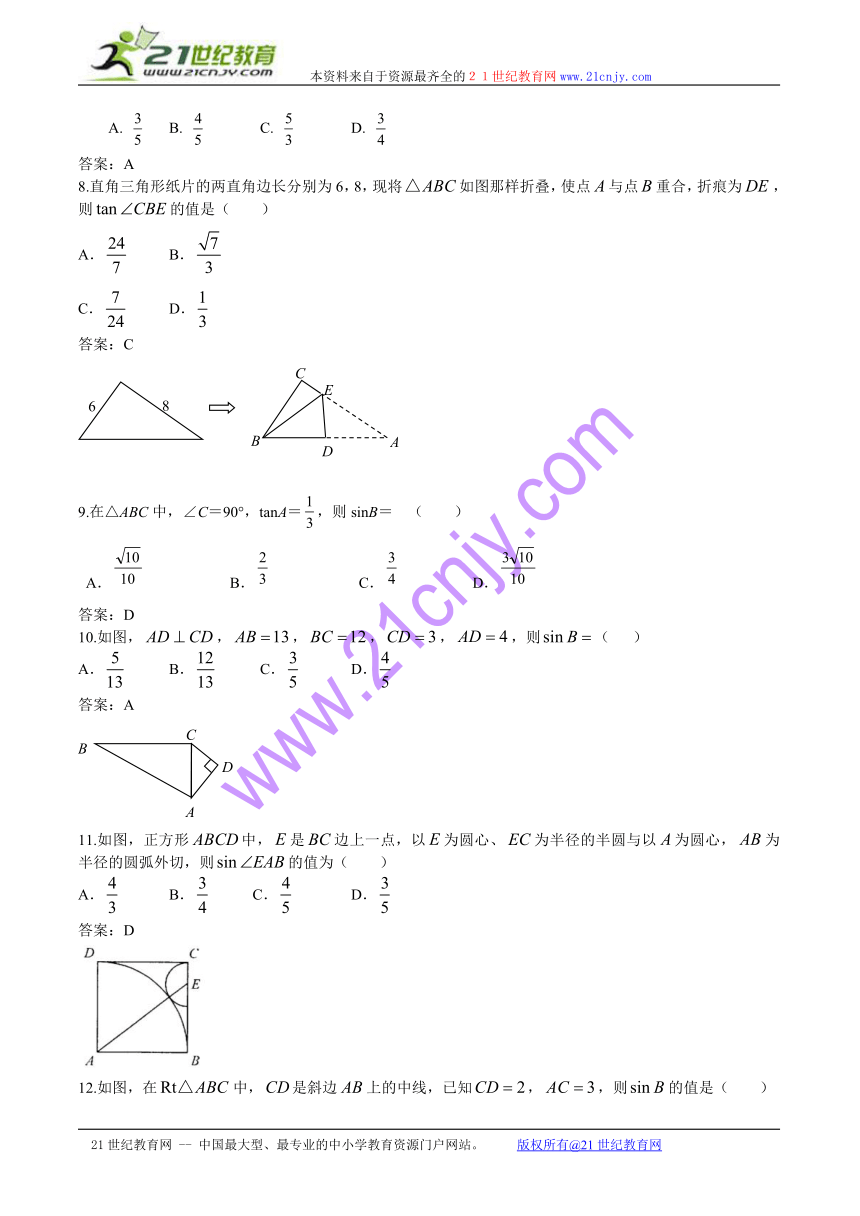
8.直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是( )
A. B.
C. D.
答案:C
9.在△ABC中,∠C=90°,tanA=,则sinB= ( )
A. B. C. D.
答案:D
10.如图,,,,,,则( )
A. B. C. D.
答案:A
11.如图,正方形中,是边上一点,以为圆心、为半径的半圆与以为圆心,为半径的圆弧外切,则的值为( )
A. B. C. D.
答案:D
12.如图,在中,是斜边上的中线,已知,,则的值是( )
A. B. C. D.
答案:C
13.如右图所示,已知⊙O是△ABC的外接圆,AD是⊙O 的直径,连接CD,若,则的值为( )
A. B. C. D.
答案:B
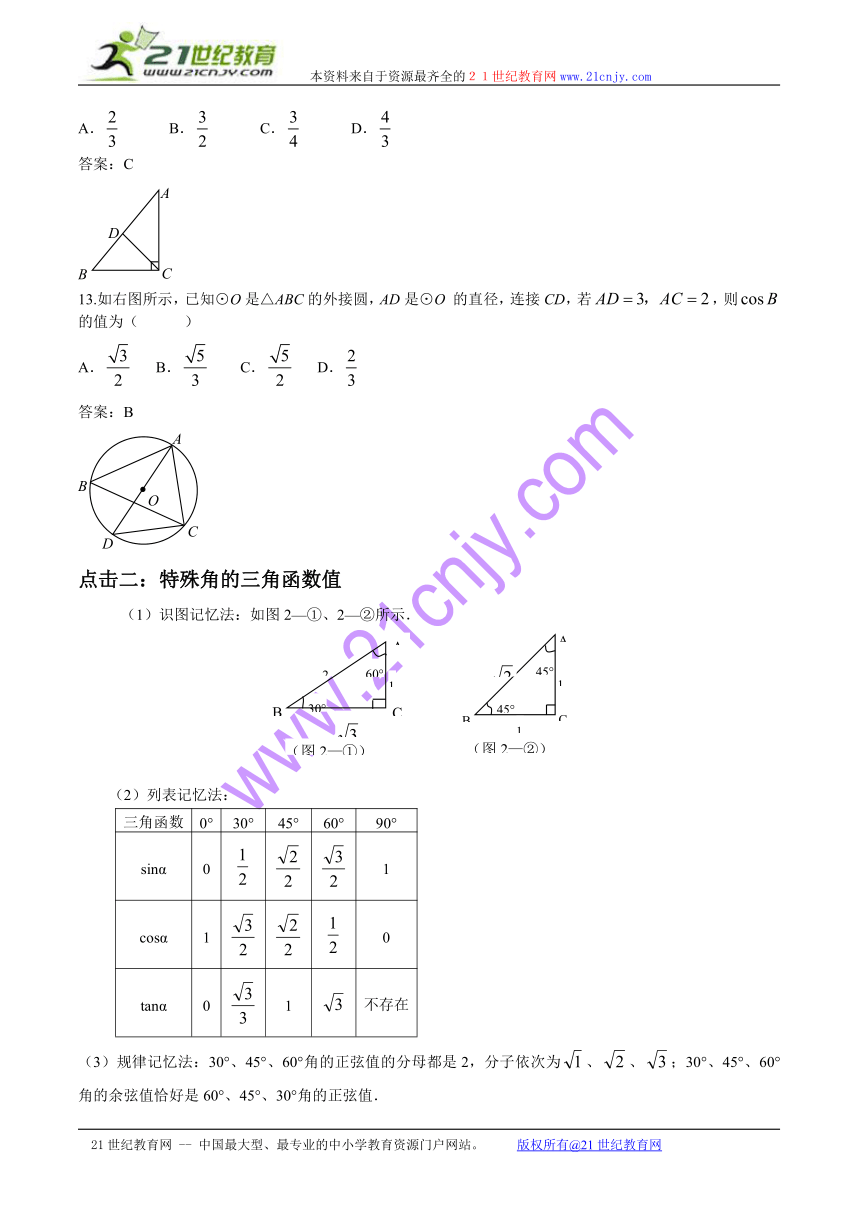
点击二:特殊角的三角函数值
(1)识图记忆法:如图2—①、2—②所示.
(2)列表记忆法:
三角函数 0° 30° 45° 60° 90°
sinα 0 1
cosα 1 0
tanα 0 1 不存在
(3)规律记忆法:30°、45°、60°角的正弦值的分母都是2,分子依次为、、;30°、45°、60°角的余弦值恰好是60°、45°、30°角的正弦值.
针对练习2:
1.如图所示,Rt△ABC∽Rt△DEF,则cosE的值等于( )
A. B.
C. D.
答案:A
2.因为,,
所以;因为,,所以,由此猜想,推理知:一般地当为锐角时有,由此可知:( )
A. B. C. D.
答案:C
3.已知为锐角,且,则等于( )
A. B. C. D.
答案:C
4.的值等于( )
A. B. C. D.
答案:B
5.已知为锐角,且cot(90°-)=,则的度数为( )
A.30° B.60° C.45° D.75°
答案:B
6.的值等于( )
A. B. C. D.1
答案:A
7.在直角坐标系中,点在第一象限内,且与轴正半轴的夹角为,则的值是( )
A. B. C. D.
答案:B
8. A(cos60°,-tan30°)关于原点对称的点A1的坐标是( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
答案:A
9. 计算: .
答案:
10. 计算:.
答案:解: 原式
点击三:三角函数关系
我们知道,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,则有:,,,这就是锐角三角函数的定义.根据锐角三角函数的定义,再结合直角三角形的性质,我们可以探索出锐角三角函数之间的三个特殊关系.
(1)余角关系
由上面的定义我们已得到sinA=cosB,cosA=sinB,而在直角三角形中,∠A+∠B=90°,即∠B=90°-∠A.因此有:sinA=cos(90°-A),cosA=sin(90°-A).应用这些关系式,可以很轻松地进行三角函数之间的转换.
(2)平方关系
由定义知,,
所以(sin2A、cos2A分别表示sinA、cosA的平方).
又由勾股定理,知a2+b2=c2,
所以sin2A+cos2A==1.
应用此关系式我们可以进行有关锐角三角函数平方的计算.
(3)相除关系
由定义中,,
得.
利用这个关系式可以使一些化简求值运算过程变得简单.
针对练习3:
1.如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,已知,BD=2,求BC的长.
解:由于∠A+∠B=90°,
所以.
在Rt△BCD中,,所以.
所以BC=4.
2. 计算:sin256°+sin245°+sin234°.
解:由余角关系知sin56°=cos(90°-56°)=cos34°.
所以原式=sin245°+(sin234°+cos234°)
.
3. 已知α为锐角,tanα=2,求的值.
解:因为,所以sinα=2cosα,
所以原式.
类型之一:锐角三角函数概念
例1:在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_________.
解析:已知Rt△ABC中, ∠C=AB=5,AC=4,可以利用勾股定理求出BC,再直接由正弦定义求解.
解答:在Rt△ABC中,因为∠C=AB=5,AC=4,所以由勾股定理,得BC=所以由正弦定义,得HYPERLINK "http://www.21cnjy.com/" EMBED Equation.3
点评:若在求解过程中不方便利用锐角三角函数的定义,可以依照题意画出草图.另外,要知道锐角三角函数的值是一个比值.
类型之二:特殊角的三角函数值的计算
例2:计算的结果是( )
A.2 B. C. D.1
解析:将对应的锐角三角函数值直接代如计算.
解答:=故应选C.
点评:特殊角的锐角三角函数的值必须熟记,才能在具体计算时少出差错.
类型之三:运用三角函数的关系化简或求值
例3:已知为锐角, sin()=0.625, 则cos=_______.
解析:利用公式sin()=cos直接求解.
解答:因为sin()=cos, sin()=0.625,所以cos=0.625.
点评:在解决此类型题时,要熟练掌握互为余角的两个角的正弦、余弦之间的关系.
一、选择题
1.在Rt△ABC中,∠C=900,∠A=∠B,则sinA的值是( ).
A. B. C. D.1
2.在△ABC中,∠A=105°,∠B=45°,tanC的值是( ).
A. B. C.1 D.
3.在Rt△ABC中,如果各边的长度都缩小至原来的,那么锐角A的各个三角函数值( ).
A.都缩小 B.都不变 C.都扩大5倍 D.仅A不变
4.如图,菱形ABCD对角线AC=6,BD=8,∠ABD=.则下列结论正确的是( ).
A.sin= B.cos= C.tan= D.tan=
5.在Rt△ABC中,斜边AB是直角边AC的3倍,下列式子正确的是( ).
A. B. C. D.
6.已知ΔABC中,∠C=90,CD是AB边上的高,则CD:CB等于( ).
A.sinA B.cosA C.tanA D.
7.等腰三角形底边长为10㎝,周长为36cm,那么底角的余弦等于( ).
A. B. C. D.
8.如图,在△EFG中,∠EFG=90°,FH⊥EG,下面等式中,错误的是( ).
A. B. C. D.
9.身高相同的三个小朋友甲、乙、丙风筝,他们放出的线长分别为300米、250米、200米,线与地面所成的角为30°、45°、60°(风筝线是拉直的),则三人所放的风筝( ).
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
10.如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将ΔEBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF等于( ).
A. B. C. D.
二、填空题
11.可用锐角的正弦表示成__________.
12.如图表示甲、乙两山坡情况,其中tan_____tanβ,_____坡更陡. (前一空填“>”“<”或“=”,后一空填“甲”“乙”)
13.在Rt△ABC中,若∠C=900,∠A=300,AC=3,则BC=__________.
14.在Rt△ABC中,∠C=900,=2, sinA=, 则c=______.
15.如图,P是∠的边OA上一点,且P点的坐标为(3,4),则sin(900 - )=_______.
16.已知tan·tan30°=1,且为锐角,则=______.
17.在△ABC中,∠A=∠B=∠C,则∠A= ,若BC=4,则AB= .
18.已知直角三角形的两直角边的比为1:7,则最小角的正弦值为__________.
三、解答题(共56分)
19.在Rt△ABC中,∠C=900,AB=13,BC=5,
求, ,.
20.计算:
(1)
(2)tan230°+cos230°-sin245°tan45°
(3)+60°
21.在△ABC中,∠C=90°,sinA=,求cosA、tanB .
22.已知为锐角,求下列各题中的度数:
(1)tan(+12°)= (2)
23.在△ABC中,内角∠A、∠B满足|sinA-|+(1-tanB)2=0,请说出△ABC的至少三个特征.
24.在△ABC中,∠C=900,a、b、c分别为∠A、∠B、∠C的对边,试证明sin2A+cos2A=1;并利用这个公式计算:若sinA= ,求cosA的值(∠A为锐角).
参考答案:
一、选择题
1.B 2.B 3.B 4.D 5.D 6.B 7.B 8.C 9.D 10.A
(提示:设AB=CD=4,AD=BC=CF=5,∵∠D=90°,∴DF==3,∴∠DCF=
二、填空题
11.60° 12.<、乙 13. 14.6 15. 16.60° 17.30°、8 18.
三、解答题
19.∵在Rt△ABC中,∠C=90°,AB=13,BC=5,∴AC==12,
∴A==,A==,A==.
20.(1)原式==
(2)原式=+-= =
(3)原式=+2×=1-+=1+
21.∵∠C=90°,∴A==,设,则,
∴=,∴A==,B===.
22.(1)∵,∴,∴;
(2),∴=或=,∵是锐角,=,∵=,∴.
23.∵=0且=0,∴,,∴∠A=60°,∠B=90°,∴∠C=30°.特征:∠A=60°,∠B=90°,∠C=30°,AC=2AB,BC=AB等等.
24.∵∠C=90°,∴A=,B=,∴A+B=+=,
∵在Rt△ABC中,∠C=90°,∴,∴A+B==1,∵A=,
∴,∴,∴,∵∠A是锐角,∴
一、选择题:
1.Rt△ABC中,若各边长都扩大2倍,则锐角A的四个三角函数值( )
A.都没有变化 B.都扩大2倍 C.都缩小2倍 D.不能确定
2.Rt△ABC中,若sinA= ,则cos的值等于( )
A. B. C. D.
3.当锐角A>60°时,∠A的余弦值 ( )
A.小于 B.大于 C.大于 D.小于
4.如图所示,为测得河两岸相对的电线杆A,B间的距离,在相距A点15m的C处测得∠ACB=50°,且AC⊥AB,则A,B间的距离应是( )
A.15sin50°m B.15cos50°m; C.15tan50°m D.15cot50°m
5.一个人从山下沿30°角的坡路向上攀登,如果在坡面上走了100米,那么他上升的高度是( )
A.100米 B.50米 C.50米 D.无法确定
6.若锐角A满足tanA-cotA=2,则tan2A+cot2A等于( )
A.6 B.4 C.2 D.0
7.∠A是锐角,tanA>,则∠A( )
A.小于30° B.大于30° C.小于60° D.大于60°
8.下列各式正确的是( )
A.sin30°+sin30°=sin60° B.tan60°-tan30°=tan30°
C.cos(60°-30°)=cos60°-cos30° D.3tg30°=
9.HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 的值等于( )
A.-1- B.- C. D.1+
10.用计算器求“已知cotα=1.515,求α”时,先计算( )
A. B.α C.HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 D.1+
二、填空题:
1.如图所示,sinD=______,cosD=_______,tanD=________,cotD=_______,
tanE=_______,sinE=________,cosE=_________,cotE=________.
2.若△ABC中,∠C=90°,则是∠A的_______函数.
3.若∠A为锐角,cosA=,则sinA=________.
4.(tan70°)2003·(3tan20°)2003=_________.
5.△ABC中,若│sinA-|+(-cosB)=0,则∠C=_______.
6.若sin(90°-α)=,则cos(90°-α)=______.
7.用不等号连接右面的式子:cos40°_____cos20°,sin37°______sin42°.
8.若tanα·tan35°=1,则锐角α的度数等于________.
三、训练平台:
(1)2sin30°-2cos60°+tan45° (2)tan30°.cot30°+sin245°+cos245°
(3)1-sin245°-cos245° (4) HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 ·cot30°
(5)2sin30°-(cos60°)-1-│-tan60°│+HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 ; (6)
(7)利用计算器计算sin55°+tan28°*cos18°(结果保留四个有效数字).
四、提高训练:
1.△ABC中,若∠A,∠B都是锐角,且sinA=,sinB=,你能判断出△ABC的形状吗
2.已知Rt△ABC中,∠C=90°,a+b=2+2,c=4,求锐角A的度数.
3.△ABC中,∠C=90°,tanA+cotB=1,求sinA+sinB的值.
4.已知一次函数y=kx+b的图象经过点P(1,2),且与x轴正半轴交于点A,与y轴正半轴交于点B,若tan∠PAO=,求点B的坐标.
五、探索发现
阅读下面的材料,再回答问题.
三角函数中,常用公式sin(α+β)=sinαcosβ+cosαsinβ求sin75°的值,
即sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°=.
请你用公式cos(α+β)=cosαcosβ-sinαsinβ求cos75°的值.
参考答案
一、1.A 2.C 3.D 4.C 5.B 6.A 7.B 8.D 9.D 10.A
二、1. 2.正切 3.
4.1 5.105° 6. 7.< < 8. 55°
三、1.(1)1. (2)2. (3)0. (4)1. (5)-2. (6)cos40°-sin40°
(7)sin55°+tan28°·cos18°≈0.81915+0.53170×0.95105≈1.325
计算过程中的数据要结果要求的精确度多取一个有效数字.
四、1.直角三角形
2.∠A=30°或∠A=60°.
3. . 4.B(0, ).
五、解:cos75°=cos(30°+45°)=cos30°·cos45°-sin30°·sin45°=.
一、填空题
1、sin53°cos37°+cos53°sin37°= .
2、如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径,,则的值是_____。
二、选择题
3、在△ABC中,∠C = 90°,∠B=50°,AB=10,则BC的长为( )
A.10tan50° B.10cos20° C.10sin50° D.
4、如图所示,AB是⊙O的直径,弦AC、BD相交于E,则等于( )
A、 B、 C、 D、
三、计算解答题
5、cos21°+cos22°+···+cos288°+cos289°.
6、如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
(1) 求证:DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3) 在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
7、已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据sin50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,cos25°=0.9063,tan25°=O.4663)
8. 如图,△ABC中,已知∠ACB=90°,CD⊥AB于D,AC=,BD=3.
(1)请根据下面求cosA的解答过程,在横线上填上适当的结论,使解答正确完整:
∵CD⊥AB,∠ACB=90°,∴AC=_____cosA,_____=. 由已知,AC=,BD=3,∴=AB =(AD+BD)=(+3).
设t=cosA,则t>0,上式可化为____________=0,
解得,(不合题意,舍去),,∴cosA=t=.
(2)求BC的长及△ABC的面积.
9.在△ABC中,∠A=1200,AB=12,AC=6.求sinB+sinC的值.
(提示:过C点作CE⊥BA交BA的延长线于E,过点B作BD⊥CA交CA的延长线于D.)
答案:
1、1;2、.3、B.4、D;
5、原式=44.5
6、(1)过A作DC的垂线AM交DC于M,
则AM=BC=2.
又tan∠ADC=2,所以.即DC=BC.
(2)等腰三角形.
证明:因为.
所以,△DEC≌△BFC
所以,.
所以,
即△ECF是等腰直角三角形.
(3)设,则,所以.
因为,又,所以.
所以
所以.
7、(1)解:连结OA
∵PA,PB是⊙O的切线
∴∠PAO=90°,∠APO=∠BPO
∵∠APB=90°
∴∠APO=45°
∴∠AOP=45°
∴OA=PA=8
∴OP=
(2)解:连结OA
∵PA,PB是⊙O的切线
∴∠APO=∠BPO=∠APB=25°
∵
∴
8.(1)AB、AD、 (2)∵cosA=,∴∠A=30°, ∵∠BCD=∠A=30°,
∠BDC=90°,∴BD=BC,∵BD=3,∴BC=6.∴△ABC的面积==.
9.∵∠BAC=120°, ∴∠DAB=∠EAC=60°,∵∠D=∠E=90°,∴∠DBA=∠ECA=30°,∵AB=12,AC=6,∴AD=6,AE=3,∴BD=,CE=,BC=,
∴SinB==,sinC==,
∴SinB+sinC=
课时作业:
A等级
一、选择题
1.中,,分别的对边,下列关系中错误的是( )
A. B. C. D.
2.如果是锐角,且,那么( )
A. B.
C. D.
3.已知,则的值等于( )
A. B. C. D.
4.如图1,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )
A. B. C. D.
5.下列说法中正确的是( )
A.在中,若,则
B.在中,若,则
C.在中,,则
D.
6.比较,,的大小关系是( )
A. B.
C. D.
二、填空题
7.在中,,且,求的三个三角函数值._______;_______;_______.
8.在中,,,,则_______.
9.中,已知,,则_______.
10.中,,,则_______.
11.在中,,,边上的高,则_______.
12. _______.
三、解答题
13.在锐角中,,,,
(1)求的值;
(2)求的值.
14.如图2,矩形中,作交于,且,试用和表示和的长.
15.已知:如图3,三个村庄在一条东西走向的公路沿线上,千米.在村的正北方向有一个村,测得,,今将区域进行规划,除其中面积为0.5平方千米的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.
(结果精确到0.1平方千米,,,)
参考答案:
一、1.A 2.C 3.D 4.A 5.C 6.B
二、7.,,, 8.
9. 10. 11. 12.
三、13.(1);(2)
14.提示:,
15.提示:平方千米
B等级
一、填空题
1.如图1中,在直角坐标系中,已知中,,,则点坐标是_______.
2.如图2,在中,,,在边上,且,,则_______.
3.如图3从位于处的某海防哨所在它的北偏东的方向,相距米的处有一艘艇正在向正南方向航行,经过若干时间快艇到达哨所东南方向的处,则间的距离是_______米.
4.如图4,中,,,为垂足,若,,则_______, _______.
二、选择题
5.已知等腰梯形的底角为,上底长为,上、下底长之比为,那么梯形的面积为( )
A. B. C. D.
6.某人沿着倾斜角为的斜坡前进米,那么他上升的高度是( )
A.米 B.米 C.米 D.米
7.如图5两建筑物的水平距离为米,从点测得点的俯角为,测得点的俯角为,则较低建筑物的高为( )
A.米 B.米 C.米 D.米
8.河堤的横断面如图6所示,堤高是5米,迎水坡的长是13米,那么斜坡的坡度是( )
A. B. C. D.
三、解答题
9.如图7,为响应市人民政府“形象重于生命”的号召,在甲建筑物从点到点挂一长为30米的宣传条幅,在乙建筑物的顶部点测得条幅顶端点的仰角为45°,测得条幅底端点的俯角为30°,求底部不能直接到达的甲、乙建筑物之间水平距离.
10.如图8,某一水库大坝的横断面是梯形,坝顶宽米,斜坡米,坝高8米,斜坡的坡度,求斜坡的坡角和坝底宽.
11.如图9,海轮在处测得北偏东45°方向上有一座灯塔,海轮向正东方向每小时18海里的速度航行,1小时30分钟后到达处,测得灯塔在北偏东15°的方向上,求塔到处的距离.(精确到0.1海里,参考数据:sin75°=0.97,cos75°=0.26,tan75°=3.73)
四、实践应用题
12.如图10,在旧城改造中,要拆除一烟囱,在地面上事先划定以为圆心,半径与等长的圆形危险区,现在从离点到21米远的建筑物顶端点测得点的仰角为,点的俯角为30°;问离点35米远的受保护文物是否在危险区内?
参考答案:
一、1. 2. 3. 4.,
二、5.A 6.D 7.D 8.C
三、9.提示:米.
10.提示:,.
11.提示:到的距离约为海里.
12.提示:不在危险区之内.
C等级
一、填空题
1、△ABC中,∠C=90°,BC=1,AC=2,则sinB=__________,tanA=_______。
2、△ABC中,∠C=90°,BC=50,AB=50,则cosB=______,tanA=____。
3、 △ABC中,三个内角之比为1∶2∶3,则对应的三边之比为__________。
4、△ABC中,∠C=90°,∠A=60°,则sinA+cosB=__________。
5、若∠A为锐角,且sinA-=0,则∠A=__________。
6、计算sin30°-cos45°=__________。
7、已知∠A为锐角,sinA=,则tgA=__________。
8、△ABC中,∠C=90°,∠A=60°,BC=1,则AB=__________。
二、选择题
9、用计算器计算的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
10、直角三角形ABC中,斜边AB是直角边BC的4倍,则cosA是 ( )
A. B. C. D.
11、在Rt△ABC中,∠C=90°,下列各式中正确的是( )
A. sinA=sinB B.sinA=cosB C.tanA=tanB D.cotA=cotB
12、△ABC中,∠C=90°,若sinA=,则tanB等于( )
A. B. C. D.
13、如图,菱形ABCD中,对角线AC=10 cm,BD=6 cm,那么sin∠DAC等于( )
A. B. C. D.
14、在△ABC中,∠C=900,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
三、解答题
15、计算:(1)4sin245°-cos30°+tan60°.
(2)-2sin45°-32.
方式一:(用计算器计算)
计算的结果是__________.
按键顺序为:
方式二:(不用计算器计算)
16、如图,是一零件图,已知∠ABC=∠BCD=90°,AB=8cm,sinA=,CD=2cm,求sin∠CBD的值。
17、如图,△ABC是一仓库的屋顶的截面图,若∠B=30°,∠C=45°,AC=2,求线段AB长。
18、求tan15°的值.(提示:先画一30°角的Rt△ABC,∠A=30°,延长CA到D,使AD=AB,构造出15°的锐角,求解)
19、如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
(2)若直线AB交x轴于点C,求△AOC的面积。
参考答案:
1、 填空题
1、,;2、,1;3、1∶∶2;4、;5、45°;6、0; 7、;8、;
二、选择题
9、B; 10、B;11、B;12、D;13、C;14、A ;
三、
15、(1)解:原式=4×-+
=2-+=2+;
(2)方式一:(用计算器计算)
计算的结果是 -9 .
按键顺序为:
方式二:(不用计算器计算)
原式=-2×-9
=--9
=-9
16、解:由 sinA==, 设BC=3,AC=5,
则根据勾股定理,得 AB==4;
∵ AB=8 cm, ∴ =2,
∴ BC=6 cm,
在Rt△BCD中,BD===4 cm;
∴ sin∠CBD===;
17、解:过A作AD⊥BC,
在Rt△ADC中,∵ ∠C=45°,
∴ sinC==,
∴ AD=,
在Rt△ABD中,∵ ∠B=30°,
∴ sinB==,
∴ AB=2AD=2.
18、解:延长CA到D,使AD=AB,则∠D=∠ABD,
∵∠BAC=30°,∴∠D=15°;设BC=1,则AB=2,AC=,
∴ tan15°=====2-.
19、解:(1)过点A作AD⊥x轴,垂足为D
则OD=OA cos60°=2×=1,
AD=OA sin60°=2×=,
∴点A的坐标为(1,)
(2)设直线AB的解析式为y=kx+b,
则有
∴直线AB的解析式为y
令x=0,得,∴
A
B
C
(图1)
∠A的对边
∠A的邻边
斜边
A
B
O
A
B
O
O
A
B
C
D
6
8
C
E
A
B
D
D
A
B
C
C
A
B
D
A
C
D
B
O
(图2—①)
(图2—②)
30°
A
B
C
60°
1
2
45°
45°
A
B
C
1
1
F
E
D
B
C
60°
C
B
A
E
F
D
C
D
B
A
O
E
C
A
B
D
A
B
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二十六章二次函数
第22课时 §28.1 锐角三角函数
本章“锐角三角函数”属于三角形,是《数学课程标准》中“空间与图形”领域的重要内容。从《数学课程标准》看,中学数学把三角形内容分成两个部分,第一部分放在义务教育阶段,第二部分放在高中阶段。在义务教育阶段,主要研究锐角三角函数和解直角三角形的内容,本套教科书安排了一章的内容,就是本章“锐角三角函数”。在高中阶段的三角内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
本章包括锐角三角函数的概念(主要是正弦、余弦和正切的概念),以及利用锐角三角函数解直角三角形等内容。锐角三角函数为解直角三角形提供了有效的工具,解直角三角形在实际当中有着广泛的应用,这也为锐角三角函数提供了与实际联系的机会。研究锐角三角函数的直接基础是相似三角形的一些结论,解直角三角形主要依赖锐角三角函数和勾股定理等内容,因此相似三角形和勾股定理等是学习本章的直接基础。本章重点是锐角三角函数的概念和直角三角形的解法。锐角三角函数的概念既是本章的难点,也是学习本章的关键。难点在于,锐角三角函数的概念反映了角度与数值之间对应的函数关系,这种角与数之间的对应关系,以及用含有几个字母的符号sinA、cosA、tanA表示函数等,学生过去没有接触过,因此对学生来讲有一定的难度。至于关键,因为只有正确掌握了锐角三角函数的概念,才能真正理解直角三角形中边、角之间的关系,从而才能利用这些关系解直角三角形。
在余弦函数和正切函数的概念给出之后,教科书在边注中分析了锐角三角函数的角与数值之间的对应关系,突出了函数的思想。一些特殊角的三角函数值是经常用到的,教科书借助于学生熟悉的两种三角尺研究了、、角的正弦、余弦和正切值,并以例题的形式介绍了已知锐角三角函数值求锐角的问题,当然这时所要求出的角都是、和的特殊角。教科书把求特殊角的三角函数值和已知特殊角的三角函数值求角这两个相反方向的问题安排在一起,目的是体现锐角三角函数中角与函数值之间的对应关系。本节最后,教科书介绍了如何使用计算器求非特殊角的三角函数值以及如何根据三角函数值求对应的角等内容。由于不同的计算器操作步骤有所不同,教科书只就常见的情况进行介绍。
在第28.1节 “锐角三角函数”中,教科书先研究了正弦函数,然后在正弦函数的基础上给出余弦函数和正切函数的概念。在第28.1节 “锐角三角函数”中,教科书先研究了正弦函数,然后在正弦函数的基础上给出余弦函数和正切函数的概念。在余弦函数和正切函数的概念给出之后,教科书在边注中分析了锐角三角函数的角与数值之间的对应关系,突出了函数的思想。一些特殊角的三角函数值是经常用到的,教科书借助于学生熟悉的两种三角尺研究了、、角的正弦、余弦和正切值,并以例题的形式介绍了已知锐角三角函数值求锐角的问题,当然这时所要求出的角都是、和的特殊角。教科书把求特殊角的三角函数值和已知特殊角的三角函数值求角这两个相反方向的问题安排在一起,目的是体现锐角三角函数中角与函数值之间的对应关系。
点击一:锐角三角函数定义
如图1,在Rt△ABC中,如果锐角A确定,那么
∠A的对边与斜边的比叫做∠A的正弦,记作sinA ,即sinA=;
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=;
∠A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA=.
锐角A的正弦、余弦和正切都是∠A的三角函数.
注意:(1)由于锐角三角函数是一种比值,因此它只有大小而没有单位;
(2)由于三角函数是一个比值,它的大小仅与角的大小有关,而与它所在的三角形的边的长度无关;
(3)sinA、cosA、tanA是一些完整的符号,不能把sinA看作sin与A的积,离开了A的sin没有任何意义,只有合起来,sinA才表示∠A的正弦. cosA、tanA也是如此.
针对练习1:
1.正方形网格中,如图放置,则的值为( )
A. B.HYPERLINK "http://www.21cnjy.com/"EMBED Unknown C. D.2
答案:A
2.正方形网格中,如图放置,则=( )
A. B.
C. D.
答案:B
3.在中,,若,则的值是( )
A. B.2 C. D.
答案:A
4.在Rt△ABC 中, ∠C=90,AB=4,AC=1,则的值是 ( )
A. B. C. D.4
答案:B
5.在正方形网格中,的位置如图所示,则的值为( )
A. B. C. D.
答案:B
6.如图,已知⊙O的半径为1,AB与⊙O相切于点A,OB与⊙O交于点C,CD⊥OA,垂足为D,则cos ∠AOB的值等于( )
A.OD B.OA C.CD D.AB
答案:A
7.已知中,AC=4,BC=3,AB=5,则( )
A. B. C. D.
答案:A
8.直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是( )
A. B.
C. D.
答案:C
9.在△ABC中,∠C=90°,tanA=,则sinB= ( )
A. B. C. D.
答案:D
10.如图,,,,,,则( )
A. B. C. D.
答案:A
11.如图,正方形中,是边上一点,以为圆心、为半径的半圆与以为圆心,为半径的圆弧外切,则的值为( )
A. B. C. D.
答案:D
12.如图,在中,是斜边上的中线,已知,,则的值是( )
A. B. C. D.
答案:C
13.如右图所示,已知⊙O是△ABC的外接圆,AD是⊙O 的直径,连接CD,若,则的值为( )
A. B. C. D.
答案:B
点击二:特殊角的三角函数值
(1)识图记忆法:如图2—①、2—②所示.
(2)列表记忆法:
三角函数 0° 30° 45° 60° 90°
sinα 0 1
cosα 1 0
tanα 0 1 不存在
(3)规律记忆法:30°、45°、60°角的正弦值的分母都是2,分子依次为、、;30°、45°、60°角的余弦值恰好是60°、45°、30°角的正弦值.
针对练习2:
1.如图所示,Rt△ABC∽Rt△DEF,则cosE的值等于( )
A. B.
C. D.
答案:A
2.因为,,
所以;因为,,所以,由此猜想,推理知:一般地当为锐角时有,由此可知:( )
A. B. C. D.
答案:C
3.已知为锐角,且,则等于( )
A. B. C. D.
答案:C
4.的值等于( )
A. B. C. D.
答案:B
5.已知为锐角,且cot(90°-)=,则的度数为( )
A.30° B.60° C.45° D.75°
答案:B
6.的值等于( )
A. B. C. D.1
答案:A
7.在直角坐标系中,点在第一象限内,且与轴正半轴的夹角为,则的值是( )
A. B. C. D.
答案:B
8. A(cos60°,-tan30°)关于原点对称的点A1的坐标是( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
答案:A
9. 计算: .
答案:
10. 计算:.
答案:解: 原式
点击三:三角函数关系
我们知道,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,则有:,,,这就是锐角三角函数的定义.根据锐角三角函数的定义,再结合直角三角形的性质,我们可以探索出锐角三角函数之间的三个特殊关系.
(1)余角关系
由上面的定义我们已得到sinA=cosB,cosA=sinB,而在直角三角形中,∠A+∠B=90°,即∠B=90°-∠A.因此有:sinA=cos(90°-A),cosA=sin(90°-A).应用这些关系式,可以很轻松地进行三角函数之间的转换.
(2)平方关系
由定义知,,
所以(sin2A、cos2A分别表示sinA、cosA的平方).
又由勾股定理,知a2+b2=c2,
所以sin2A+cos2A==1.
应用此关系式我们可以进行有关锐角三角函数平方的计算.
(3)相除关系
由定义中,,
得.
利用这个关系式可以使一些化简求值运算过程变得简单.
针对练习3:
1.如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,已知,BD=2,求BC的长.
解:由于∠A+∠B=90°,
所以.
在Rt△BCD中,,所以.
所以BC=4.
2. 计算:sin256°+sin245°+sin234°.
解:由余角关系知sin56°=cos(90°-56°)=cos34°.
所以原式=sin245°+(sin234°+cos234°)
.
3. 已知α为锐角,tanα=2,求的值.
解:因为,所以sinα=2cosα,
所以原式.
类型之一:锐角三角函数概念
例1:在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_________.
解析:已知Rt△ABC中, ∠C=AB=5,AC=4,可以利用勾股定理求出BC,再直接由正弦定义求解.
解答:在Rt△ABC中,因为∠C=AB=5,AC=4,所以由勾股定理,得BC=所以由正弦定义,得HYPERLINK "http://www.21cnjy.com/" EMBED Equation.3
点评:若在求解过程中不方便利用锐角三角函数的定义,可以依照题意画出草图.另外,要知道锐角三角函数的值是一个比值.
类型之二:特殊角的三角函数值的计算
例2:计算的结果是( )
A.2 B. C. D.1
解析:将对应的锐角三角函数值直接代如计算.
解答:=故应选C.
点评:特殊角的锐角三角函数的值必须熟记,才能在具体计算时少出差错.
类型之三:运用三角函数的关系化简或求值
例3:已知为锐角, sin()=0.625, 则cos=_______.
解析:利用公式sin()=cos直接求解.
解答:因为sin()=cos, sin()=0.625,所以cos=0.625.
点评:在解决此类型题时,要熟练掌握互为余角的两个角的正弦、余弦之间的关系.
一、选择题
1.在Rt△ABC中,∠C=900,∠A=∠B,则sinA的值是( ).
A. B. C. D.1
2.在△ABC中,∠A=105°,∠B=45°,tanC的值是( ).
A. B. C.1 D.
3.在Rt△ABC中,如果各边的长度都缩小至原来的,那么锐角A的各个三角函数值( ).
A.都缩小 B.都不变 C.都扩大5倍 D.仅A不变
4.如图,菱形ABCD对角线AC=6,BD=8,∠ABD=.则下列结论正确的是( ).
A.sin= B.cos= C.tan= D.tan=
5.在Rt△ABC中,斜边AB是直角边AC的3倍,下列式子正确的是( ).
A. B. C. D.
6.已知ΔABC中,∠C=90,CD是AB边上的高,则CD:CB等于( ).
A.sinA B.cosA C.tanA D.
7.等腰三角形底边长为10㎝,周长为36cm,那么底角的余弦等于( ).
A. B. C. D.
8.如图,在△EFG中,∠EFG=90°,FH⊥EG,下面等式中,错误的是( ).
A. B. C. D.
9.身高相同的三个小朋友甲、乙、丙风筝,他们放出的线长分别为300米、250米、200米,线与地面所成的角为30°、45°、60°(风筝线是拉直的),则三人所放的风筝( ).
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
10.如图,已知矩形ABCD的两边AB与BC的比为4:5,E是AB上的一点,沿CE将ΔEBC向上翻折,若B点恰好落在边AD上的F点,则tan∠DCF等于( ).
A. B. C. D.
二、填空题
11.可用锐角的正弦表示成__________.
12.如图表示甲、乙两山坡情况,其中tan_____tanβ,_____坡更陡. (前一空填“>”“<”或“=”,后一空填“甲”“乙”)
13.在Rt△ABC中,若∠C=900,∠A=300,AC=3,则BC=__________.
14.在Rt△ABC中,∠C=900,=2, sinA=, 则c=______.
15.如图,P是∠的边OA上一点,且P点的坐标为(3,4),则sin(900 - )=_______.
16.已知tan·tan30°=1,且为锐角,则=______.
17.在△ABC中,∠A=∠B=∠C,则∠A= ,若BC=4,则AB= .
18.已知直角三角形的两直角边的比为1:7,则最小角的正弦值为__________.
三、解答题(共56分)
19.在Rt△ABC中,∠C=900,AB=13,BC=5,
求, ,.
20.计算:
(1)
(2)tan230°+cos230°-sin245°tan45°
(3)+60°
21.在△ABC中,∠C=90°,sinA=,求cosA、tanB .
22.已知为锐角,求下列各题中的度数:
(1)tan(+12°)= (2)
23.在△ABC中,内角∠A、∠B满足|sinA-|+(1-tanB)2=0,请说出△ABC的至少三个特征.
24.在△ABC中,∠C=900,a、b、c分别为∠A、∠B、∠C的对边,试证明sin2A+cos2A=1;并利用这个公式计算:若sinA= ,求cosA的值(∠A为锐角).
参考答案:
一、选择题
1.B 2.B 3.B 4.D 5.D 6.B 7.B 8.C 9.D 10.A
(提示:设AB=CD=4,AD=BC=CF=5,∵∠D=90°,∴DF==3,∴∠DCF=
二、填空题
11.60° 12.<、乙 13. 14.6 15. 16.60° 17.30°、8 18.
三、解答题
19.∵在Rt△ABC中,∠C=90°,AB=13,BC=5,∴AC==12,
∴A==,A==,A==.
20.(1)原式==
(2)原式=+-= =
(3)原式=+2×=1-+=1+
21.∵∠C=90°,∴A==,设,则,
∴=,∴A==,B===.
22.(1)∵,∴,∴;
(2),∴=或=,∵是锐角,=,∵=,∴.
23.∵=0且=0,∴,,∴∠A=60°,∠B=90°,∴∠C=30°.特征:∠A=60°,∠B=90°,∠C=30°,AC=2AB,BC=AB等等.
24.∵∠C=90°,∴A=,B=,∴A+B=+=,
∵在Rt△ABC中,∠C=90°,∴,∴A+B==1,∵A=,
∴,∴,∴,∵∠A是锐角,∴
一、选择题:
1.Rt△ABC中,若各边长都扩大2倍,则锐角A的四个三角函数值( )
A.都没有变化 B.都扩大2倍 C.都缩小2倍 D.不能确定
2.Rt△ABC中,若sinA= ,则cos的值等于( )
A. B. C. D.
3.当锐角A>60°时,∠A的余弦值 ( )
A.小于 B.大于 C.大于 D.小于
4.如图所示,为测得河两岸相对的电线杆A,B间的距离,在相距A点15m的C处测得∠ACB=50°,且AC⊥AB,则A,B间的距离应是( )
A.15sin50°m B.15cos50°m; C.15tan50°m D.15cot50°m
5.一个人从山下沿30°角的坡路向上攀登,如果在坡面上走了100米,那么他上升的高度是( )
A.100米 B.50米 C.50米 D.无法确定
6.若锐角A满足tanA-cotA=2,则tan2A+cot2A等于( )
A.6 B.4 C.2 D.0
7.∠A是锐角,tanA>,则∠A( )
A.小于30° B.大于30° C.小于60° D.大于60°
8.下列各式正确的是( )
A.sin30°+sin30°=sin60° B.tan60°-tan30°=tan30°
C.cos(60°-30°)=cos60°-cos30° D.3tg30°=
9.HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 的值等于( )
A.-1- B.- C. D.1+
10.用计算器求“已知cotα=1.515,求α”时,先计算( )
A. B.α C.HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 D.1+
二、填空题:
1.如图所示,sinD=______,cosD=_______,tanD=________,cotD=_______,
tanE=_______,sinE=________,cosE=_________,cotE=________.
2.若△ABC中,∠C=90°,则是∠A的_______函数.
3.若∠A为锐角,cosA=,则sinA=________.
4.(tan70°)2003·(3tan20°)2003=_________.
5.△ABC中,若│sinA-|+(-cosB)=0,则∠C=_______.
6.若sin(90°-α)=,则cos(90°-α)=______.
7.用不等号连接右面的式子:cos40°_____cos20°,sin37°______sin42°.
8.若tanα·tan35°=1,则锐角α的度数等于________.
三、训练平台:
(1)2sin30°-2cos60°+tan45° (2)tan30°.cot30°+sin245°+cos245°
(3)1-sin245°-cos245° (4) HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 ·cot30°
(5)2sin30°-(cos60°)-1-│-tan60°│+HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 ; (6)
(7)利用计算器计算sin55°+tan28°*cos18°(结果保留四个有效数字).
四、提高训练:
1.△ABC中,若∠A,∠B都是锐角,且sinA=,sinB=,你能判断出△ABC的形状吗
2.已知Rt△ABC中,∠C=90°,a+b=2+2,c=4,求锐角A的度数.
3.△ABC中,∠C=90°,tanA+cotB=1,求sinA+sinB的值.
4.已知一次函数y=kx+b的图象经过点P(1,2),且与x轴正半轴交于点A,与y轴正半轴交于点B,若tan∠PAO=,求点B的坐标.
五、探索发现
阅读下面的材料,再回答问题.
三角函数中,常用公式sin(α+β)=sinαcosβ+cosαsinβ求sin75°的值,
即sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°=.
请你用公式cos(α+β)=cosαcosβ-sinαsinβ求cos75°的值.
参考答案
一、1.A 2.C 3.D 4.C 5.B 6.A 7.B 8.D 9.D 10.A
二、1. 2.正切 3.
4.1 5.105° 6. 7.< < 8. 55°
三、1.(1)1. (2)2. (3)0. (4)1. (5)-2. (6)cos40°-sin40°
(7)sin55°+tan28°·cos18°≈0.81915+0.53170×0.95105≈1.325
计算过程中的数据要结果要求的精确度多取一个有效数字.
四、1.直角三角形
2.∠A=30°或∠A=60°.
3. . 4.B(0, ).
五、解:cos75°=cos(30°+45°)=cos30°·cos45°-sin30°·sin45°=.
一、填空题
1、sin53°cos37°+cos53°sin37°= .
2、如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径,,则的值是_____。
二、选择题
3、在△ABC中,∠C = 90°,∠B=50°,AB=10,则BC的长为( )
A.10tan50° B.10cos20° C.10sin50° D.
4、如图所示,AB是⊙O的直径,弦AC、BD相交于E,则等于( )
A、 B、 C、 D、
三、计算解答题
5、cos21°+cos22°+···+cos288°+cos289°.
6、如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
(1) 求证:DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3) 在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
7、已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据sin50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,cos25°=0.9063,tan25°=O.4663)
8. 如图,△ABC中,已知∠ACB=90°,CD⊥AB于D,AC=,BD=3.
(1)请根据下面求cosA的解答过程,在横线上填上适当的结论,使解答正确完整:
∵CD⊥AB,∠ACB=90°,∴AC=_____cosA,_____=. 由已知,AC=,BD=3,∴=AB =(AD+BD)=(+3).
设t=cosA,则t>0,上式可化为____________=0,
解得,(不合题意,舍去),,∴cosA=t=.
(2)求BC的长及△ABC的面积.
9.在△ABC中,∠A=1200,AB=12,AC=6.求sinB+sinC的值.
(提示:过C点作CE⊥BA交BA的延长线于E,过点B作BD⊥CA交CA的延长线于D.)
答案:
1、1;2、.3、B.4、D;
5、原式=44.5
6、(1)过A作DC的垂线AM交DC于M,
则AM=BC=2.
又tan∠ADC=2,所以.即DC=BC.
(2)等腰三角形.
证明:因为.
所以,△DEC≌△BFC
所以,.
所以,
即△ECF是等腰直角三角形.
(3)设,则,所以.
因为,又,所以.
所以
所以.
7、(1)解:连结OA
∵PA,PB是⊙O的切线
∴∠PAO=90°,∠APO=∠BPO
∵∠APB=90°
∴∠APO=45°
∴∠AOP=45°
∴OA=PA=8
∴OP=
(2)解:连结OA
∵PA,PB是⊙O的切线
∴∠APO=∠BPO=∠APB=25°
∵
∴
8.(1)AB、AD、 (2)∵cosA=,∴∠A=30°, ∵∠BCD=∠A=30°,
∠BDC=90°,∴BD=BC,∵BD=3,∴BC=6.∴△ABC的面积==.
9.∵∠BAC=120°, ∴∠DAB=∠EAC=60°,∵∠D=∠E=90°,∴∠DBA=∠ECA=30°,∵AB=12,AC=6,∴AD=6,AE=3,∴BD=,CE=,BC=,
∴SinB==,sinC==,
∴SinB+sinC=
课时作业:
A等级
一、选择题
1.中,,分别的对边,下列关系中错误的是( )
A. B. C. D.
2.如果是锐角,且,那么( )
A. B.
C. D.
3.已知,则的值等于( )
A. B. C. D.
4.如图1,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )
A. B. C. D.
5.下列说法中正确的是( )
A.在中,若,则
B.在中,若,则
C.在中,,则
D.
6.比较,,的大小关系是( )
A. B.
C. D.
二、填空题
7.在中,,且,求的三个三角函数值._______;_______;_______.
8.在中,,,,则_______.
9.中,已知,,则_______.
10.中,,,则_______.
11.在中,,,边上的高,则_______.
12. _______.
三、解答题
13.在锐角中,,,,
(1)求的值;
(2)求的值.
14.如图2,矩形中,作交于,且,试用和表示和的长.
15.已知:如图3,三个村庄在一条东西走向的公路沿线上,千米.在村的正北方向有一个村,测得,,今将区域进行规划,除其中面积为0.5平方千米的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.
(结果精确到0.1平方千米,,,)
参考答案:
一、1.A 2.C 3.D 4.A 5.C 6.B
二、7.,,, 8.
9. 10. 11. 12.
三、13.(1);(2)
14.提示:,
15.提示:平方千米
B等级
一、填空题
1.如图1中,在直角坐标系中,已知中,,,则点坐标是_______.
2.如图2,在中,,,在边上,且,,则_______.
3.如图3从位于处的某海防哨所在它的北偏东的方向,相距米的处有一艘艇正在向正南方向航行,经过若干时间快艇到达哨所东南方向的处,则间的距离是_______米.
4.如图4,中,,,为垂足,若,,则_______, _______.
二、选择题
5.已知等腰梯形的底角为,上底长为,上、下底长之比为,那么梯形的面积为( )
A. B. C. D.
6.某人沿着倾斜角为的斜坡前进米,那么他上升的高度是( )
A.米 B.米 C.米 D.米
7.如图5两建筑物的水平距离为米,从点测得点的俯角为,测得点的俯角为,则较低建筑物的高为( )
A.米 B.米 C.米 D.米
8.河堤的横断面如图6所示,堤高是5米,迎水坡的长是13米,那么斜坡的坡度是( )
A. B. C. D.
三、解答题
9.如图7,为响应市人民政府“形象重于生命”的号召,在甲建筑物从点到点挂一长为30米的宣传条幅,在乙建筑物的顶部点测得条幅顶端点的仰角为45°,测得条幅底端点的俯角为30°,求底部不能直接到达的甲、乙建筑物之间水平距离.
10.如图8,某一水库大坝的横断面是梯形,坝顶宽米,斜坡米,坝高8米,斜坡的坡度,求斜坡的坡角和坝底宽.
11.如图9,海轮在处测得北偏东45°方向上有一座灯塔,海轮向正东方向每小时18海里的速度航行,1小时30分钟后到达处,测得灯塔在北偏东15°的方向上,求塔到处的距离.(精确到0.1海里,参考数据:sin75°=0.97,cos75°=0.26,tan75°=3.73)
四、实践应用题
12.如图10,在旧城改造中,要拆除一烟囱,在地面上事先划定以为圆心,半径与等长的圆形危险区,现在从离点到21米远的建筑物顶端点测得点的仰角为,点的俯角为30°;问离点35米远的受保护文物是否在危险区内?
参考答案:
一、1. 2. 3. 4.,
二、5.A 6.D 7.D 8.C
三、9.提示:米.
10.提示:,.
11.提示:到的距离约为海里.
12.提示:不在危险区之内.
C等级
一、填空题
1、△ABC中,∠C=90°,BC=1,AC=2,则sinB=__________,tanA=_______。
2、△ABC中,∠C=90°,BC=50,AB=50,则cosB=______,tanA=____。
3、 △ABC中,三个内角之比为1∶2∶3,则对应的三边之比为__________。
4、△ABC中,∠C=90°,∠A=60°,则sinA+cosB=__________。
5、若∠A为锐角,且sinA-=0,则∠A=__________。
6、计算sin30°-cos45°=__________。
7、已知∠A为锐角,sinA=,则tgA=__________。
8、△ABC中,∠C=90°,∠A=60°,BC=1,则AB=__________。
二、选择题
9、用计算器计算的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
10、直角三角形ABC中,斜边AB是直角边BC的4倍,则cosA是 ( )
A. B. C. D.
11、在Rt△ABC中,∠C=90°,下列各式中正确的是( )
A. sinA=sinB B.sinA=cosB C.tanA=tanB D.cotA=cotB
12、△ABC中,∠C=90°,若sinA=,则tanB等于( )
A. B. C. D.
13、如图,菱形ABCD中,对角线AC=10 cm,BD=6 cm,那么sin∠DAC等于( )
A. B. C. D.
14、在△ABC中,∠C=900,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
三、解答题
15、计算:(1)4sin245°-cos30°+tan60°.
(2)-2sin45°-32.
方式一:(用计算器计算)
计算的结果是__________.
按键顺序为:
方式二:(不用计算器计算)
16、如图,是一零件图,已知∠ABC=∠BCD=90°,AB=8cm,sinA=,CD=2cm,求sin∠CBD的值。
17、如图,△ABC是一仓库的屋顶的截面图,若∠B=30°,∠C=45°,AC=2,求线段AB长。
18、求tan15°的值.(提示:先画一30°角的Rt△ABC,∠A=30°,延长CA到D,使AD=AB,构造出15°的锐角,求解)
19、如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
(2)若直线AB交x轴于点C,求△AOC的面积。
参考答案:
1、 填空题
1、,;2、,1;3、1∶∶2;4、;5、45°;6、0; 7、;8、;
二、选择题
9、B; 10、B;11、B;12、D;13、C;14、A ;
三、
15、(1)解:原式=4×-+
=2-+=2+;
(2)方式一:(用计算器计算)
计算的结果是 -9 .
按键顺序为:
方式二:(不用计算器计算)
原式=-2×-9
=--9
=-9
16、解:由 sinA==, 设BC=3,AC=5,
则根据勾股定理,得 AB==4;
∵ AB=8 cm, ∴ =2,
∴ BC=6 cm,
在Rt△BCD中,BD===4 cm;
∴ sin∠CBD===;
17、解:过A作AD⊥BC,
在Rt△ADC中,∵ ∠C=45°,
∴ sinC==,
∴ AD=,
在Rt△ABD中,∵ ∠B=30°,
∴ sinB==,
∴ AB=2AD=2.
18、解:延长CA到D,使AD=AB,则∠D=∠ABD,
∵∠BAC=30°,∴∠D=15°;设BC=1,则AB=2,AC=,
∴ tan15°=====2-.
19、解:(1)过点A作AD⊥x轴,垂足为D
则OD=OA cos60°=2×=1,
AD=OA sin60°=2×=,
∴点A的坐标为(1,)
(2)设直线AB的解析式为y=kx+b,
则有
∴直线AB的解析式为y
令x=0,得,∴
A
B
C
(图1)
∠A的对边
∠A的邻边
斜边
A
B
O
A
B
O
O
A
B
C
D
6
8
C
E
A
B
D
D
A
B
C
C
A
B
D
A
C
D
B
O
(图2—①)
(图2—②)
30°
A
B
C
60°
1
2
45°
45°
A
B
C
1
1
F
E
D
B
C
60°
C
B
A
E
F
D
C
D
B
A
O
E
C
A
B
D
A
B
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
