29.2三视图(含课题学习制作立体模型)
文档属性
| 名称 | 29.2三视图(含课题学习制作立体模型) |

|
|
| 格式 | rar | ||
| 文件大小 | 752.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-13 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二十九章投影与视图
第25课时 §29.2 三视图
§29.3 课题学习 制作立体模
三视图是主视图、俯视图、左视图的统称,它是从三个方向分别表示物体的形状的一种常见的视图。三视图中的三个视图的区别是:它们的哦投影方向也既是看物体的方向不同;联系是它们是同一物体的投影;位置和大小关系是长对正,高平齐,宽相等。画图时规定看得见的轮廓线化成实线,因被其它部分遮挡而看不见的轮廓线画成虚线。
由三视图确定几何体的形状,是把几何体的三个方面形状综合起来的过程,这个过程与由几何体画三视图的过程正好相反。
点击一:三视图
当我们从某一个角度观察一个物体时,所看到的图像叫做物体的一个视图。视图也可以看做物体在某一角度的光线下的投影,其中正对着我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面。一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图叫做俯视图;在侧面内得到的由左向右观察物体的视图叫做左视图。
将三个投影面展开在一个平面内,得到这一物体的一张三视图。
注意:(1)主视图反映的是物体的长和高;俯视图反映的是物体的长和宽;左视图反映的是物体的宽和高. 因此,在画三种视图时,主、俯视图要长对正,主、左视图要高平齐,俯、左视图要宽相等.
(2)三视图与投影密切相关,某些物体的三视图实际上是该物体在一定条件下所形成的平行投影,某些物体的主视图、俯视图、左视图可以看成在一束平行光线分别从物体的正面,左面上面照射下,在垂直于这一方向的平面上所形成的投影。
针对练习1:
1.如图1,一个碗摆放在桌面上,则它的俯视图是( )
答案:C
2. 如图的几何体的俯视图是( )
答案:A
3.如图①是一些大小相同的小正方体组成的几何体,其主视图如图②所示,则其俯视图是( )
答案:B
4. 右图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
A.
B. C. D.
答案:A
5. 下面左图所示的几何体的俯视图是( )
答案:D
6.左下图是由若干个小正方形所搭成的几何体及从上面看这个几何体所看到的图形,那么从左边看这个几何体时, 所看到的几何图形是( )
答案:B
7. 下列各几何体均由三个大小相同的正方体组成,其中正视图为右图的是( )
答案:A
8.如图所示的几何体的俯视图是( )
答案:C
点击二:基本几何体的三视图
基本几何体包括圆柱、圆锥、球、直棱柱、圆台,它们的三视图是画复杂几何体三视图的基础
基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆和一个点。
(4)四棱锥的三视图中有两个是三角形,另一个是矩形和它的对角线。
(5)球体的三视图都是圆形。
针对练习2:
(1)如左图,这个几何体的主视图是( )
答案:A
2.如图所示的物体是一个几何体,其主视图是( )
答案:C
3.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是( )
答案:C
4. 如图,圆柱的左视图是( )
A. B. C. D.
答案:C
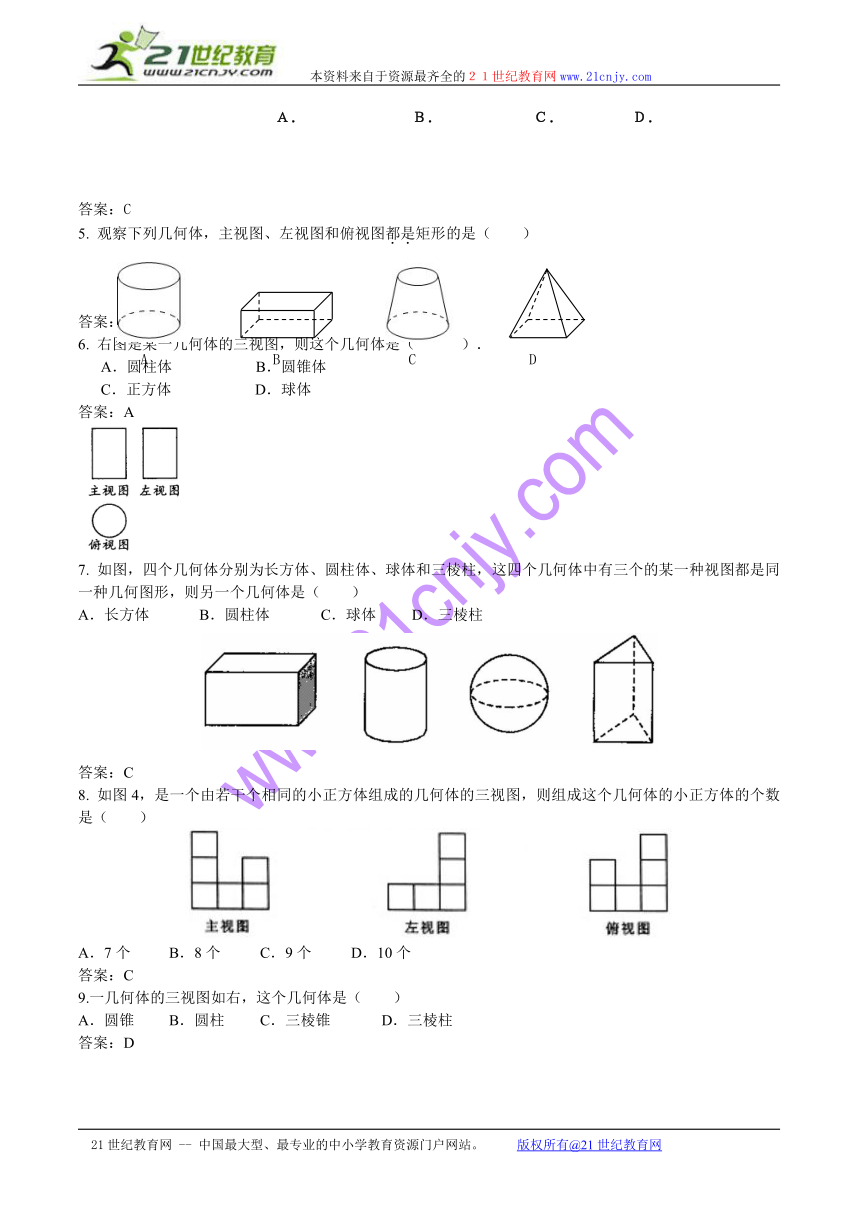
5. 观察下列几何体,主视图、左视图和俯视图都是矩形的是( )
答案:B
6. 右图是某一几何体的三视图,则这个几何体是( ).
A.圆柱体 B.圆锥体
C.正方体 D.球体
答案:A
7. 如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是( )
A.长方体 B.圆柱体 C.球体 D.三棱柱
答案:C
8. 如图4,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( )
A.7个 B.8个 C.9个 D.10个
答案:C
9.一几何体的三视图如右,这个几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
答案:D
10. 与左图中的三视图相对应的几何体是( )
答案:D
点击三:几何体三视图的画法
画这些基本几何体的三视图时,要注意从三个方面观察它们,具体画法为:
1.确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
1.将如图所示的Rt△ABC绕直角边BC旋转一周,所得几何体的左视图是( )
答案:A
2. 如下图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )
A. B. C. D.
答案:A
3. 图(1),(2),(3),(4)四个几何体的三视图为以下四组平面图形,其中与图(3)对应的三视图是( )
答案:A
4. 六个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( )
A.正视图的面积最大
B.左视图的面积最大
C.俯视图的面积最大
D.三个视图的面积一样大
答案:C
5. 如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是( )
A. B.
C. D.
答案:D
6. 如图是一个包装盒的三视图,则这个包装盒的体积是( )
A. 1000πcm3 B. 1500πcm3 C. 2000πcm3 D. 4000πcm3
答案:C
7. 某几何体的三视图如下所示,则该几何体可以是( )
答案:A
8. 在生活和生产实践中,我们经常需要运用三视图来描述物体的形状和大小.小亮在观察左边的热水瓶时,得到的左视图是( )
答案:B
类型之一:根据物体(几何体)画三种视图
例1: 小明从正面观察如图1所示的两个物体,看到的是( )
解析:本题是由正面观察两个物体,所以小明看到的图形应是物体的主视图.从正面看圆柱,所得的图形是长方形;从正面看正方体,所得的图形为正方形,所以小明从正面看到的图形应是两个,左边为长方形,右边为正方形,
答案:C.
例2 如图2,水杯的俯视图是( )
解析:物体的俯视图就是从实物的上面看到的图形,从水杯正上面往下看,看到的一定是水杯圆形的上口和圆形的水杯底及右侧的杯柄,而不是长方形或带杯柄的长方形.观察四个选项符合题意的只有D
答案:D.
例3:我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图3,从图的左面看这个几何体的所得左视图是( )
解析:从左面看,从后至前共有两列,从上至下共有三行,即所画的立体图形的左视图有两列三行.第一列上有3个正方形,第二列上有1个正方形
答案:B.
类型之二:根据三种视图确定物体(几何体)的形状
例4:如果某物体的三种视图是如图4所示的三个图形,那么该物体的形状是( )
A.正方体 B.长方体
C.三棱柱 D.圆锥
解 析:从图4的主视图和左视图以及俯视图看,原几何体是一个柱体,由于主视图和左视图都是长方形,俯视图是三角形,所以几何体为三棱柱
答案:C.
类型之三:根据三种视图确定组成原几何体的小正方体的个数
例5:由几个相同的小正方体搭成的几何体的三种视图如图5所示,则搭成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.7
解析:要解决这类问题应做到,一看俯视图,从左至右共两列,从上到下共两行;二看主视图共两列三行,并且第一列上有3个正方形,第二列上有1个正方形,则俯视图第一列上必定有一个数字为3,第二列上的数字为1;三看左视图共两列三行,第一列上有3个正方形,第二列上有1个正方形,则俯视图第一行上必有数字3,第二行上的数字为1,所以该俯视图上每个小正方形的数字(层数)应为:搭成这个几何体的小正方体的个数是3+1+1=5
答案:B.
类型之四:根据俯视图及其各位置上小正方体的个数确定几何体的主视图或左视图
例6: 如图7是几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的主视图为( )
解析:这类题目,在俯视图上都标有其相应位置上的小立方体块的个数(即层数).画图原则:通常是把俯视图画在主视图的下边,左视图画在主视图的右边.其具体画法是先确定俯视图有几列,则其主视图就有几列,然后根据俯视图每一列上对应数字的大小来确定主视图相对应的列上要画几个小正方形即该列上有几层.本题几何体的俯视图从左至右共有三列,则对应的主视图应有三列,本题几何体的俯视图第一列上数字为1,则其主视图第一列上要画1个正方形即该列上有1层,本题几何体的俯视图第二列上最大数字为2,则其主视图第二列上要画2个正方形即该列上有2层,本题几何体的俯视图第三列上最大数字为1,则其主视图第三列上要画1个正方形,即该列上有1层
答案:A.
类型之五:根据视图计算体积
例:图5是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积。(结果保留)
解析:根据立体图形的三视图,计算立体图的体积,首先要根据三视图确定立体图形的形状,然后再根据相应的计算公式计算。观察三视图可知原立体图形是圆柱,其中圆柱的高为10,圆柱底面圆的直径为10,根据圆柱的体积计算公式可以计算出该圆柱的体积。
解:这个立体图形为圆柱,其中高是10,底面圆的半径为5,
所以体积为π×52×10=250π。 图5
评注:根据三视图计算几何体的体积,首先根据三视图确定原几何体的形状,然后再根据所给出的尺寸的大小,代入相应的公式进行计算。
1.小明从正面观察图1所示的两个物体,看到的是下图中的( )
2.图2是空心圆柱体在指定方向上的视图,如图正确的是( )
3.将如图3所示放置的一个直角三角形ABC( ∠C=90°),绕斜边AB旋转一周所得到的几何体的主视图是图中四个图形中的_________(只填序号).
4.如图4,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB、DC重合,则所围成的几何体图形是图中的( )
5.如图,是由一些相同的小立方块搭成的立体图形的三种视图,则搭成这个立体图形的小立方块的个数是( )
A.5 B.6 C.7 D.8
6.如图所示,说出下列四个图形各是由哪些立体图形展开得到的?
7.如图所示,画出该物体的三视图
8.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
答案: 1.C 2.C 3.(2) 4.D 5.D
6.长方形 圆柱 三棱柱 四棱锥 7.略 8.(1)略 (2)8、9、10、11
一、认认真真,书写快乐
1.如图1,圆锥的左视图是 .
2.圆柱的左视图是 ,俯视图是 .
3.主视图、左视图和俯视图都是圆的几何体是 ,主视图、左视图和俯视图都是正方形的几何体是 .
4.如图2是某几何体的三种视图,这个几何体是 .
5.图3是某几何体的三视图,则该几何体是 .
二、仔仔细细,记录自信
6.图4中几何体的主视图是( )
7.如图5所示几何体的左视图是( )
8.如图6所示的正四棱锥的俯视图是( )
9.某同学所画的如图7所示几何体的三种视图如下:(不考虑尺寸)
在这三种视图中,正确的是( )
A.①② B.①③ C.②③ D.②
10.按图8摆放的球、圆锥、圆台的俯视图是( )
三、平心静气,展示智慧
11.如图9所示,在公园的石凳子上放着一个篮球,画出它们组合体的三视图:
12.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图10所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
13.一个透明的几何体如图11,粗线表示一根嵌在几何体内的铁丝,右边是它的主视图,请你画出它的左视图和俯视图,并用色笔标明铁丝位置.
参考答案:
一、1.等腰三角形 2.长方形,圆 3.球,正方体 4.圆柱
5.六棱柱
二、6.C 7.C 8.D 9.B 10.A
三、11.图略。
12.(1)
(2)的值可以是8,9,10,11。
13.
1.如图,这个几何体的俯视图是( )C
2.我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )B
3.如图是由几个小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,那么这个几何体的主视图是( )B
4.如图所示物体的主视图是( )A
5.由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法
正确的是( )C
A. 主视图的面积最大 B. 左视图的面积最大
C. 俯视图的面积最大 D. 三个视图的面积一样大。
6.桌上摆放着一个由若干个相同正方形组成的几何体,其正视图和左视图如下所示,这个几何体最多可由______个这样的正方体,最少可由______个这样的正方体。 13;7
7. 由几个相同的小正方体叠成的一个几何体,它的三种视图如下,那么这个几何体是由_______个小正方体组成。5
8. 如图,是由一些完全相同的小立方体搭成的几何体的三种视图,那么搭成这个几何体所用的小立方体个数是________8
9 .如图正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,所得圆柱的主视图的周长是__________________12
10.如图,是某工件的三视图,求此工件的全面积及体积。
面积:
体积:
11.如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE)。广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC。一辆以60km/h匀速行驶的汽车经过公路段BC的时间是3s,已知广告牌和公路的距离为40m,求小华家到公路的距离。(精确到1m)133m
12.求如图所示的三视图所表示的物体的体积和表面积。体积:
表面积:
课时作业:
课时作业A
1.三视图位置有规定:主视图要在______,它的下方应是______,______坐落在右边.
2.主视图反映物体的_______和_______,俯视图反映物体的______和______,左视图反映物体的________和_______.因此,必须注意主视图与俯视图的长对正,主视图与________的高平齐,左视图与_______的宽相等.
3.根据下列物体的三视图,填出几何体的名称:
(1)如图7所示的几何体是______.
(2)如图8所示的几何体是______.
4.小琳过14周岁生日,父母为她预定的生日蛋糕如图9所示,它的主视图应该是()
5.某物体三视图如图10,则该物体形状可能是( )
A.长方体 B.圆锥体 C.立方体 D.圆柱体
6.,如图11是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( )
A.4个 B.5个 C.6个 D.7个
7.如果用“■”表示1个立方体,用“▓”表示两个立方体叠加,用“■”表示三个立方体叠加,那么如图12由6个立方体叠成的几何体的主视图是如图13所示的( )
8.如图14的右图是一只小动物正在观看另一只小动物用锯子分割立方体,小明随即编了一道题:若把立方体①截去若干部分,分别得到图②、③、④、⑤的物体,请画出图②、③、④、⑤的物体的俯视图.
9.画出如图15所示立体图形的三视图.
10.如图16是某物体的三种视图,请描述这个物体的形状,并画出其图形.
11.由6个大小相同的正方体搭成的几何体如图16所示,则关于它的视图说法正确的是( )
A.正视图的面积最大 B.左视图的面积最大
C.俯视图的面积最大 D.三个视图的面积一样大
12.如图17,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( )
A.5m B.6m C.7m D.8m
13.如图18是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是( )
A.24πcm3 B.48πcm3 C.72πcm3 D.192πcm3
14.如图19,一个圆柱的轴截面平行于投影面,圆柱的正投影是边长为4的正方形.求圆柱的体积和表面积.
15.如图20这是一个几何体的二视图,求该几何体的体积(π取3.14).
16.分别画出如图21所示几何体的三视图,并求几何体的表面积和体积.
17.如图22,由物体的展开图,画出物体的三视图,并求其体积.
课时作业A答案:
1.左上边、俯视图、左视图;2.长、高、长、宽、高、度、左视图、俯视;3.六棱柱、圆台;4.B;5.A;6.D;7.B;8.如图:
9,(1)如图:
(2)如图:
(3)如图:
(4)如图:
10,其形状为一个圆柱体和一个长方体的组合图形,其图形如图:
11.C;12.D;13.B;14.体积为16π(立方单位),表面积为24π(平方单位);15.V=V圆柱体+V长方体=π(HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 )2×32+30×25×40=40048(cm3).答:该几何体的体积为40048cm3;16.如图:①表面积为208cm2,体积为192cm3,②表面积为247.5cm2,体积为141.75cm3;③表面积为460+36π≈573cm2,体积为(1500-135π)≈538cm3;
17.如图:体积为cm3,体积约为18.36cm2.
课时作业B
1.一个正方体的面共有( )
A.1个 B.2个 C.4个 D.6个
答案:D
2.下列物体的形状类似于球的是( ).
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
答案:C
3.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体( )
A.4个 B.8个 C.16个 D.27个
答案:B
4.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 (填 “相同”、“不一定相同”、“不相同”之一).
答案:相同
5.如图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 .
答案:24
6.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是 cm2.
答案:6
7.展览厅内要用相同的正方体木块搭成一个三视图如右图的展台,则此展台共需这样的正方体______块.
答案:10
8.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是 .
答案:
9.右图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 .
答案:
10.一个几何体的三视图如图所示,则这个几何体的名称是 .
答案:直三棱柱
11.下图是某几何体的展开图.
(1)这个几何体的名称是 ;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(取3.14)
答案:(1)圆柱;
(2)三视图为:
(3)体积为:==1570.
课时作业C
1. 小琳过14周岁生日,父母为她预定的生日蛋糕如图所示,它的主视图应该是 ( )
2.某物体三视图如图,则该物体形状可能是 ( )
(A)长方体.
(B)圆锥体.
(C)立方体.
(D)圆柱体.
3.下图是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( )
(A)4个. (B)5个. (C)6个. (D)7个.
4.如果用 表示1个立方体,用 表示两个立方体叠加,用 表示三个立方体叠加,那么下图由6个立方体叠成的几何体的主视图是 ( )
5.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是 ( )
6.小明从正面观察下图所示的两个物体,看到的是 ( )
7.有一实物如图,那么它的主视图是 ( )
8.如图是正三菱柱,它的主视图正确的是
( )
9.两个物体的主视图都是圆,则这两个物体
可能是( )
(A)圆柱体、圆锥体. (B)圆柱体、正方体.
(C)圆柱体、球. (D)圆锥体、球.
10.由若干个同样大小的正方体堆积成一个实
物,不同侧面观察到如下投影图,则构成该
实物的小正方体个数为 ( )
(A)6. (B)7. (C)8. (D)9.
11.我们常说的三种视图是指 .
12.请写出三种视图都相同的两种几何体是 .
13.棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积是 .
14.一个物体的俯视图是圆,则该物体有可能是 (写两个即可).
15.一个几何体的三视图如下,那么这个几何体是 .
16.图中四个图形是多面体的展开图,你能说出这些多面体的名称吗
17.画出如图所示中立体图形的三视图.
课时作业C答案:
1.B 2.A 3.D 4.B 5.A 6.C 7.B 8.B 9.D 10.B 11.主视图 俯视图 左视图 12.球、正方体 13.36cm2 14.球 圆柱体 圆锥体等 15.圆锥体 16.略 17.略
A.
B.
C.
D.
图①
图②
A. B. C. D.
2
1
3
A.
B.
C.
D.
从左面看
A.
D.
B.
C.
从正面看
从上面看
A.
B.
C.
D.
A.
B.
C.
D.
a
a
a
A. B. C. D.
A. B. C. D.
左面
A.
B.
C.
D.
A
B
D
C
俯视图
左
视
图
主
视
图
A.
B.
C.
D.
D
A
B
C
C
B
A
主视图
左视图
俯视图
1
1
1
1
2
2
(1)
(2)
(3)
(4)
A.
B.
C.
D.
主视图
左视图
俯视图
主视图
左视图
俯视图
A.
B.
C.
D.
图7
图8
蛋糕 A B C D
图9
图10
图11
图12 A B C D
图13
① ② ③ ④ ⑤
图14
图15
图16
图16
图17
图18
图19
图21
图20
图22
③
4
2
正
视
图
左
视
图
俯
视
图
8
8
13
20
10
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二十九章投影与视图
第25课时 §29.2 三视图
§29.3 课题学习 制作立体模
三视图是主视图、俯视图、左视图的统称,它是从三个方向分别表示物体的形状的一种常见的视图。三视图中的三个视图的区别是:它们的哦投影方向也既是看物体的方向不同;联系是它们是同一物体的投影;位置和大小关系是长对正,高平齐,宽相等。画图时规定看得见的轮廓线化成实线,因被其它部分遮挡而看不见的轮廓线画成虚线。
由三视图确定几何体的形状,是把几何体的三个方面形状综合起来的过程,这个过程与由几何体画三视图的过程正好相反。
点击一:三视图
当我们从某一个角度观察一个物体时,所看到的图像叫做物体的一个视图。视图也可以看做物体在某一角度的光线下的投影,其中正对着我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面。一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图叫做俯视图;在侧面内得到的由左向右观察物体的视图叫做左视图。
将三个投影面展开在一个平面内,得到这一物体的一张三视图。
注意:(1)主视图反映的是物体的长和高;俯视图反映的是物体的长和宽;左视图反映的是物体的宽和高. 因此,在画三种视图时,主、俯视图要长对正,主、左视图要高平齐,俯、左视图要宽相等.
(2)三视图与投影密切相关,某些物体的三视图实际上是该物体在一定条件下所形成的平行投影,某些物体的主视图、俯视图、左视图可以看成在一束平行光线分别从物体的正面,左面上面照射下,在垂直于这一方向的平面上所形成的投影。
针对练习1:
1.如图1,一个碗摆放在桌面上,则它的俯视图是( )
答案:C
2. 如图的几何体的俯视图是( )
答案:A
3.如图①是一些大小相同的小正方体组成的几何体,其主视图如图②所示,则其俯视图是( )
答案:B
4. 右图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
A.
B. C. D.
答案:A
5. 下面左图所示的几何体的俯视图是( )
答案:D
6.左下图是由若干个小正方形所搭成的几何体及从上面看这个几何体所看到的图形,那么从左边看这个几何体时, 所看到的几何图形是( )
答案:B
7. 下列各几何体均由三个大小相同的正方体组成,其中正视图为右图的是( )
答案:A
8.如图所示的几何体的俯视图是( )
答案:C
点击二:基本几何体的三视图
基本几何体包括圆柱、圆锥、球、直棱柱、圆台,它们的三视图是画复杂几何体三视图的基础
基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆和一个点。
(4)四棱锥的三视图中有两个是三角形,另一个是矩形和它的对角线。
(5)球体的三视图都是圆形。
针对练习2:
(1)如左图,这个几何体的主视图是( )
答案:A
2.如图所示的物体是一个几何体,其主视图是( )
答案:C
3.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是( )
答案:C
4. 如图,圆柱的左视图是( )
A. B. C. D.
答案:C
5. 观察下列几何体,主视图、左视图和俯视图都是矩形的是( )
答案:B
6. 右图是某一几何体的三视图,则这个几何体是( ).
A.圆柱体 B.圆锥体
C.正方体 D.球体
答案:A
7. 如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是( )
A.长方体 B.圆柱体 C.球体 D.三棱柱
答案:C
8. 如图4,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( )
A.7个 B.8个 C.9个 D.10个
答案:C
9.一几何体的三视图如右,这个几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
答案:D
10. 与左图中的三视图相对应的几何体是( )
答案:D
点击三:几何体三视图的画法
画这些基本几何体的三视图时,要注意从三个方面观察它们,具体画法为:
1.确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
1.将如图所示的Rt△ABC绕直角边BC旋转一周,所得几何体的左视图是( )
答案:A
2. 如下图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )
A. B. C. D.
答案:A
3. 图(1),(2),(3),(4)四个几何体的三视图为以下四组平面图形,其中与图(3)对应的三视图是( )
答案:A
4. 六个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( )
A.正视图的面积最大
B.左视图的面积最大
C.俯视图的面积最大
D.三个视图的面积一样大
答案:C
5. 如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是( )
A. B.
C. D.
答案:D
6. 如图是一个包装盒的三视图,则这个包装盒的体积是( )
A. 1000πcm3 B. 1500πcm3 C. 2000πcm3 D. 4000πcm3
答案:C
7. 某几何体的三视图如下所示,则该几何体可以是( )
答案:A
8. 在生活和生产实践中,我们经常需要运用三视图来描述物体的形状和大小.小亮在观察左边的热水瓶时,得到的左视图是( )
答案:B
类型之一:根据物体(几何体)画三种视图
例1: 小明从正面观察如图1所示的两个物体,看到的是( )
解析:本题是由正面观察两个物体,所以小明看到的图形应是物体的主视图.从正面看圆柱,所得的图形是长方形;从正面看正方体,所得的图形为正方形,所以小明从正面看到的图形应是两个,左边为长方形,右边为正方形,
答案:C.
例2 如图2,水杯的俯视图是( )
解析:物体的俯视图就是从实物的上面看到的图形,从水杯正上面往下看,看到的一定是水杯圆形的上口和圆形的水杯底及右侧的杯柄,而不是长方形或带杯柄的长方形.观察四个选项符合题意的只有D
答案:D.
例3:我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图3,从图的左面看这个几何体的所得左视图是( )
解析:从左面看,从后至前共有两列,从上至下共有三行,即所画的立体图形的左视图有两列三行.第一列上有3个正方形,第二列上有1个正方形
答案:B.
类型之二:根据三种视图确定物体(几何体)的形状
例4:如果某物体的三种视图是如图4所示的三个图形,那么该物体的形状是( )
A.正方体 B.长方体
C.三棱柱 D.圆锥
解 析:从图4的主视图和左视图以及俯视图看,原几何体是一个柱体,由于主视图和左视图都是长方形,俯视图是三角形,所以几何体为三棱柱
答案:C.
类型之三:根据三种视图确定组成原几何体的小正方体的个数
例5:由几个相同的小正方体搭成的几何体的三种视图如图5所示,则搭成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.7
解析:要解决这类问题应做到,一看俯视图,从左至右共两列,从上到下共两行;二看主视图共两列三行,并且第一列上有3个正方形,第二列上有1个正方形,则俯视图第一列上必定有一个数字为3,第二列上的数字为1;三看左视图共两列三行,第一列上有3个正方形,第二列上有1个正方形,则俯视图第一行上必有数字3,第二行上的数字为1,所以该俯视图上每个小正方形的数字(层数)应为:搭成这个几何体的小正方体的个数是3+1+1=5
答案:B.
类型之四:根据俯视图及其各位置上小正方体的个数确定几何体的主视图或左视图
例6: 如图7是几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的主视图为( )
解析:这类题目,在俯视图上都标有其相应位置上的小立方体块的个数(即层数).画图原则:通常是把俯视图画在主视图的下边,左视图画在主视图的右边.其具体画法是先确定俯视图有几列,则其主视图就有几列,然后根据俯视图每一列上对应数字的大小来确定主视图相对应的列上要画几个小正方形即该列上有几层.本题几何体的俯视图从左至右共有三列,则对应的主视图应有三列,本题几何体的俯视图第一列上数字为1,则其主视图第一列上要画1个正方形即该列上有1层,本题几何体的俯视图第二列上最大数字为2,则其主视图第二列上要画2个正方形即该列上有2层,本题几何体的俯视图第三列上最大数字为1,则其主视图第三列上要画1个正方形,即该列上有1层
答案:A.
类型之五:根据视图计算体积
例:图5是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积。(结果保留)
解析:根据立体图形的三视图,计算立体图的体积,首先要根据三视图确定立体图形的形状,然后再根据相应的计算公式计算。观察三视图可知原立体图形是圆柱,其中圆柱的高为10,圆柱底面圆的直径为10,根据圆柱的体积计算公式可以计算出该圆柱的体积。
解:这个立体图形为圆柱,其中高是10,底面圆的半径为5,
所以体积为π×52×10=250π。 图5
评注:根据三视图计算几何体的体积,首先根据三视图确定原几何体的形状,然后再根据所给出的尺寸的大小,代入相应的公式进行计算。
1.小明从正面观察图1所示的两个物体,看到的是下图中的( )
2.图2是空心圆柱体在指定方向上的视图,如图正确的是( )
3.将如图3所示放置的一个直角三角形ABC( ∠C=90°),绕斜边AB旋转一周所得到的几何体的主视图是图中四个图形中的_________(只填序号).
4.如图4,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB、DC重合,则所围成的几何体图形是图中的( )
5.如图,是由一些相同的小立方块搭成的立体图形的三种视图,则搭成这个立体图形的小立方块的个数是( )
A.5 B.6 C.7 D.8
6.如图所示,说出下列四个图形各是由哪些立体图形展开得到的?
7.如图所示,画出该物体的三视图
8.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
答案: 1.C 2.C 3.(2) 4.D 5.D
6.长方形 圆柱 三棱柱 四棱锥 7.略 8.(1)略 (2)8、9、10、11
一、认认真真,书写快乐
1.如图1,圆锥的左视图是 .
2.圆柱的左视图是 ,俯视图是 .
3.主视图、左视图和俯视图都是圆的几何体是 ,主视图、左视图和俯视图都是正方形的几何体是 .
4.如图2是某几何体的三种视图,这个几何体是 .
5.图3是某几何体的三视图,则该几何体是 .
二、仔仔细细,记录自信
6.图4中几何体的主视图是( )
7.如图5所示几何体的左视图是( )
8.如图6所示的正四棱锥的俯视图是( )
9.某同学所画的如图7所示几何体的三种视图如下:(不考虑尺寸)
在这三种视图中,正确的是( )
A.①② B.①③ C.②③ D.②
10.按图8摆放的球、圆锥、圆台的俯视图是( )
三、平心静气,展示智慧
11.如图9所示,在公园的石凳子上放着一个篮球,画出它们组合体的三视图:
12.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图10所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
13.一个透明的几何体如图11,粗线表示一根嵌在几何体内的铁丝,右边是它的主视图,请你画出它的左视图和俯视图,并用色笔标明铁丝位置.
参考答案:
一、1.等腰三角形 2.长方形,圆 3.球,正方体 4.圆柱
5.六棱柱
二、6.C 7.C 8.D 9.B 10.A
三、11.图略。
12.(1)
(2)的值可以是8,9,10,11。
13.
1.如图,这个几何体的俯视图是( )C
2.我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )B
3.如图是由几个小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,那么这个几何体的主视图是( )B
4.如图所示物体的主视图是( )A
5.由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法
正确的是( )C
A. 主视图的面积最大 B. 左视图的面积最大
C. 俯视图的面积最大 D. 三个视图的面积一样大。
6.桌上摆放着一个由若干个相同正方形组成的几何体,其正视图和左视图如下所示,这个几何体最多可由______个这样的正方体,最少可由______个这样的正方体。 13;7
7. 由几个相同的小正方体叠成的一个几何体,它的三种视图如下,那么这个几何体是由_______个小正方体组成。5
8. 如图,是由一些完全相同的小立方体搭成的几何体的三种视图,那么搭成这个几何体所用的小立方体个数是________8
9 .如图正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,所得圆柱的主视图的周长是__________________12
10.如图,是某工件的三视图,求此工件的全面积及体积。
面积:
体积:
11.如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE)。广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC。一辆以60km/h匀速行驶的汽车经过公路段BC的时间是3s,已知广告牌和公路的距离为40m,求小华家到公路的距离。(精确到1m)133m
12.求如图所示的三视图所表示的物体的体积和表面积。体积:
表面积:
课时作业:
课时作业A
1.三视图位置有规定:主视图要在______,它的下方应是______,______坐落在右边.
2.主视图反映物体的_______和_______,俯视图反映物体的______和______,左视图反映物体的________和_______.因此,必须注意主视图与俯视图的长对正,主视图与________的高平齐,左视图与_______的宽相等.
3.根据下列物体的三视图,填出几何体的名称:
(1)如图7所示的几何体是______.
(2)如图8所示的几何体是______.
4.小琳过14周岁生日,父母为她预定的生日蛋糕如图9所示,它的主视图应该是()
5.某物体三视图如图10,则该物体形状可能是( )
A.长方体 B.圆锥体 C.立方体 D.圆柱体
6.,如图11是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( )
A.4个 B.5个 C.6个 D.7个
7.如果用“■”表示1个立方体,用“▓”表示两个立方体叠加,用“■”表示三个立方体叠加,那么如图12由6个立方体叠成的几何体的主视图是如图13所示的( )
8.如图14的右图是一只小动物正在观看另一只小动物用锯子分割立方体,小明随即编了一道题:若把立方体①截去若干部分,分别得到图②、③、④、⑤的物体,请画出图②、③、④、⑤的物体的俯视图.
9.画出如图15所示立体图形的三视图.
10.如图16是某物体的三种视图,请描述这个物体的形状,并画出其图形.
11.由6个大小相同的正方体搭成的几何体如图16所示,则关于它的视图说法正确的是( )
A.正视图的面积最大 B.左视图的面积最大
C.俯视图的面积最大 D.三个视图的面积一样大
12.如图17,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( )
A.5m B.6m C.7m D.8m
13.如图18是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是( )
A.24πcm3 B.48πcm3 C.72πcm3 D.192πcm3
14.如图19,一个圆柱的轴截面平行于投影面,圆柱的正投影是边长为4的正方形.求圆柱的体积和表面积.
15.如图20这是一个几何体的二视图,求该几何体的体积(π取3.14).
16.分别画出如图21所示几何体的三视图,并求几何体的表面积和体积.
17.如图22,由物体的展开图,画出物体的三视图,并求其体积.
课时作业A答案:
1.左上边、俯视图、左视图;2.长、高、长、宽、高、度、左视图、俯视;3.六棱柱、圆台;4.B;5.A;6.D;7.B;8.如图:
9,(1)如图:
(2)如图:
(3)如图:
(4)如图:
10,其形状为一个圆柱体和一个长方体的组合图形,其图形如图:
11.C;12.D;13.B;14.体积为16π(立方单位),表面积为24π(平方单位);15.V=V圆柱体+V长方体=π(HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 )2×32+30×25×40=40048(cm3).答:该几何体的体积为40048cm3;16.如图:①表面积为208cm2,体积为192cm3,②表面积为247.5cm2,体积为141.75cm3;③表面积为460+36π≈573cm2,体积为(1500-135π)≈538cm3;
17.如图:体积为cm3,体积约为18.36cm2.
课时作业B
1.一个正方体的面共有( )
A.1个 B.2个 C.4个 D.6个
答案:D
2.下列物体的形状类似于球的是( ).
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
答案:C
3.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体( )
A.4个 B.8个 C.16个 D.27个
答案:B
4.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 (填 “相同”、“不一定相同”、“不相同”之一).
答案:相同
5.如图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 .
答案:24
6.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是 cm2.
答案:6
7.展览厅内要用相同的正方体木块搭成一个三视图如右图的展台,则此展台共需这样的正方体______块.
答案:10
8.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是 .
答案:
9.右图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 .
答案:
10.一个几何体的三视图如图所示,则这个几何体的名称是 .
答案:直三棱柱
11.下图是某几何体的展开图.
(1)这个几何体的名称是 ;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(取3.14)
答案:(1)圆柱;
(2)三视图为:
(3)体积为:==1570.
课时作业C
1. 小琳过14周岁生日,父母为她预定的生日蛋糕如图所示,它的主视图应该是 ( )
2.某物体三视图如图,则该物体形状可能是 ( )
(A)长方体.
(B)圆锥体.
(C)立方体.
(D)圆柱体.
3.下图是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( )
(A)4个. (B)5个. (C)6个. (D)7个.
4.如果用 表示1个立方体,用 表示两个立方体叠加,用 表示三个立方体叠加,那么下图由6个立方体叠成的几何体的主视图是 ( )
5.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是 ( )
6.小明从正面观察下图所示的两个物体,看到的是 ( )
7.有一实物如图,那么它的主视图是 ( )
8.如图是正三菱柱,它的主视图正确的是
( )
9.两个物体的主视图都是圆,则这两个物体
可能是( )
(A)圆柱体、圆锥体. (B)圆柱体、正方体.
(C)圆柱体、球. (D)圆锥体、球.
10.由若干个同样大小的正方体堆积成一个实
物,不同侧面观察到如下投影图,则构成该
实物的小正方体个数为 ( )
(A)6. (B)7. (C)8. (D)9.
11.我们常说的三种视图是指 .
12.请写出三种视图都相同的两种几何体是 .
13.棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积是 .
14.一个物体的俯视图是圆,则该物体有可能是 (写两个即可).
15.一个几何体的三视图如下,那么这个几何体是 .
16.图中四个图形是多面体的展开图,你能说出这些多面体的名称吗
17.画出如图所示中立体图形的三视图.
课时作业C答案:
1.B 2.A 3.D 4.B 5.A 6.C 7.B 8.B 9.D 10.B 11.主视图 俯视图 左视图 12.球、正方体 13.36cm2 14.球 圆柱体 圆锥体等 15.圆锥体 16.略 17.略
A.
B.
C.
D.
图①
图②
A. B. C. D.
2
1
3
A.
B.
C.
D.
从左面看
A.
D.
B.
C.
从正面看
从上面看
A.
B.
C.
D.
A.
B.
C.
D.
a
a
a
A. B. C. D.
A. B. C. D.
左面
A.
B.
C.
D.
A
B
D
C
俯视图
左
视
图
主
视
图
A.
B.
C.
D.
D
A
B
C
C
B
A
主视图
左视图
俯视图
1
1
1
1
2
2
(1)
(2)
(3)
(4)
A.
B.
C.
D.
主视图
左视图
俯视图
主视图
左视图
俯视图
A.
B.
C.
D.
图7
图8
蛋糕 A B C D
图9
图10
图11
图12 A B C D
图13
① ② ③ ④ ⑤
图14
图15
图16
图16
图17
图18
图19
图21
图20
图22
③
4
2
正
视
图
左
视
图
俯
视
图
8
8
13
20
10
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
