数学:2.3.1《双曲线及其标准方程》课件(新人教a版选修2-1)
文档属性
| 名称 | 数学:2.3.1《双曲线及其标准方程》课件(新人教a版选修2-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 164.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-15 00:00:00 | ||
图片预览





文档简介
课件14张PPT。2.3双曲线及其标准方程一、复习回顾:1、椭圆的第一定义
2、椭圆的标准方程思考:
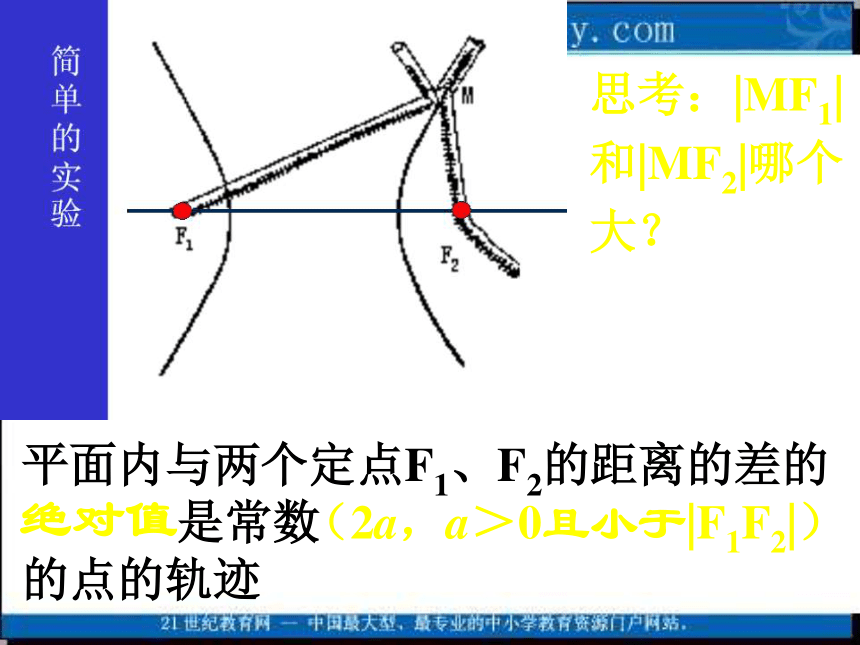
若改为“到两定点的距离差为常数”,这样的点的轨迹怎样?方程又怎样?思考:|MF1|
和|MF2|哪个
大? 平面内与两个定点F1、F2的距离的差的
是常数
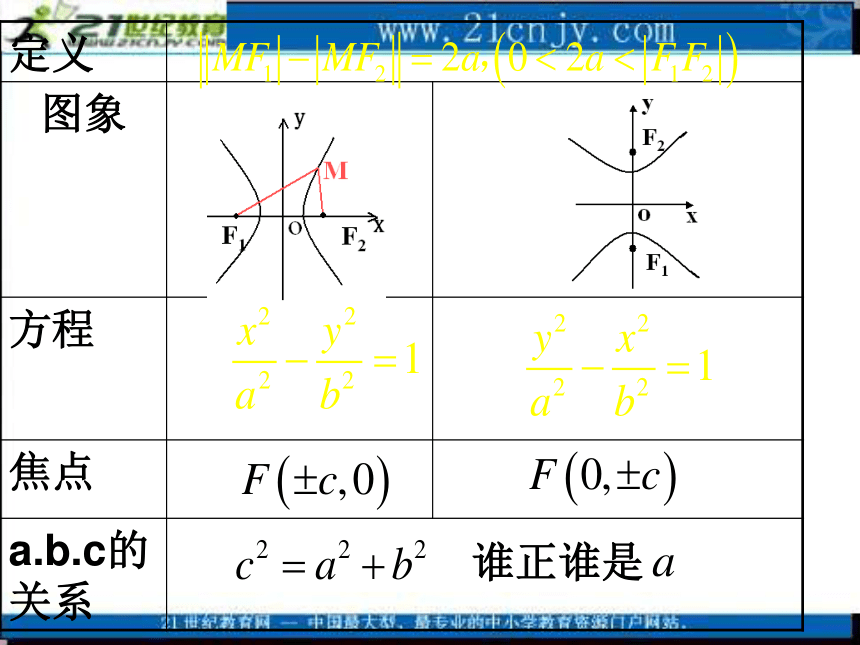
的点的轨迹绝对值(2a,a>0且小于|F1F2|)二、双曲线的定义平面内与两个定点F1、F2的距离的差的
绝对值是常数(2a,a>0且小于|F1F2|)
的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,
两个焦点的距离|F1F2|叫做双曲线的焦距。谁正谁是 动点M的轨迹是分别以点F1、F2为端点,
方向指向F1F2外侧的两条射线.动点M的轨迹不存在. 2)当2a>|F1F2|时,动点M的轨迹是什么?1)当2a=|F1F2|时,动点M的轨迹是什么?3)若常数2a=0,轨迹是什么?线段F1F2的垂直平分线思考:(4)定义中绝对值去掉有什么变化?(5)双曲线和椭圆有何不同之处?例1:求下列符合条件的双曲线标准方程:
(1)以椭圆 的焦点为顶
点,顶点为焦点;(2)过点(3)经过点练习:若 表
示双曲线,求实数m的取值范围。例2: (1)已知两点F1(-5,0),F2(5,0),求与这两点的距离的差的绝对值是6的点的轨迹方程。(2)双曲线
的过焦点F1的弦AB长为m(A,B在同一支上),另一焦点为F2,则△ABF2的周长为__________.(4)求与⊙C1:(x+3)2+y2=1和⊙C2:(x-3)2+y2=9都外切的圆M的圆心M的轨迹方程。(3)双曲线 的两
个焦点F1,F2,A是双曲线上的一点,且|AF1|=8,则|AF2|=_______.例3:已知双曲线
的左、右焦点为F1,F2,点P在双曲线上,∠F1PF2=60°,求△F1PF2的面积。例4:某工程要挖一个横截面为半圆的柱形隧道,挖出的土只能沿道路AP,BP运到P处(如图),PA=100m,PB=150m, ∠APB=60°,试说明怎样运土才能最省工。
2、椭圆的标准方程思考:
若改为“到两定点的距离差为常数”,这样的点的轨迹怎样?方程又怎样?思考:|MF1|
和|MF2|哪个
大? 平面内与两个定点F1、F2的距离的差的
是常数
的点的轨迹绝对值(2a,a>0且小于|F1F2|)二、双曲线的定义平面内与两个定点F1、F2的距离的差的
绝对值是常数(2a,a>0且小于|F1F2|)
的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,
两个焦点的距离|F1F2|叫做双曲线的焦距。谁正谁是 动点M的轨迹是分别以点F1、F2为端点,
方向指向F1F2外侧的两条射线.动点M的轨迹不存在. 2)当2a>|F1F2|时,动点M的轨迹是什么?1)当2a=|F1F2|时,动点M的轨迹是什么?3)若常数2a=0,轨迹是什么?线段F1F2的垂直平分线思考:(4)定义中绝对值去掉有什么变化?(5)双曲线和椭圆有何不同之处?例1:求下列符合条件的双曲线标准方程:
(1)以椭圆 的焦点为顶
点,顶点为焦点;(2)过点(3)经过点练习:若 表
示双曲线,求实数m的取值范围。例2: (1)已知两点F1(-5,0),F2(5,0),求与这两点的距离的差的绝对值是6的点的轨迹方程。(2)双曲线
的过焦点F1的弦AB长为m(A,B在同一支上),另一焦点为F2,则△ABF2的周长为__________.(4)求与⊙C1:(x+3)2+y2=1和⊙C2:(x-3)2+y2=9都外切的圆M的圆心M的轨迹方程。(3)双曲线 的两
个焦点F1,F2,A是双曲线上的一点,且|AF1|=8,则|AF2|=_______.例3:已知双曲线
的左、右焦点为F1,F2,点P在双曲线上,∠F1PF2=60°,求△F1PF2的面积。例4:某工程要挖一个横截面为半圆的柱形隧道,挖出的土只能沿道路AP,BP运到P处(如图),PA=100m,PB=150m, ∠APB=60°,试说明怎样运土才能最省工。
