数学:2.3.2《抛物线的简单几何性质》课件(2)(新人教a版选修1-1)
文档属性
| 名称 | 数学:2.3.2《抛物线的简单几何性质》课件(2)(新人教a版选修1-1) |  | |
| 格式 | rar | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-15 08:17:00 | ||
图片预览







文档简介
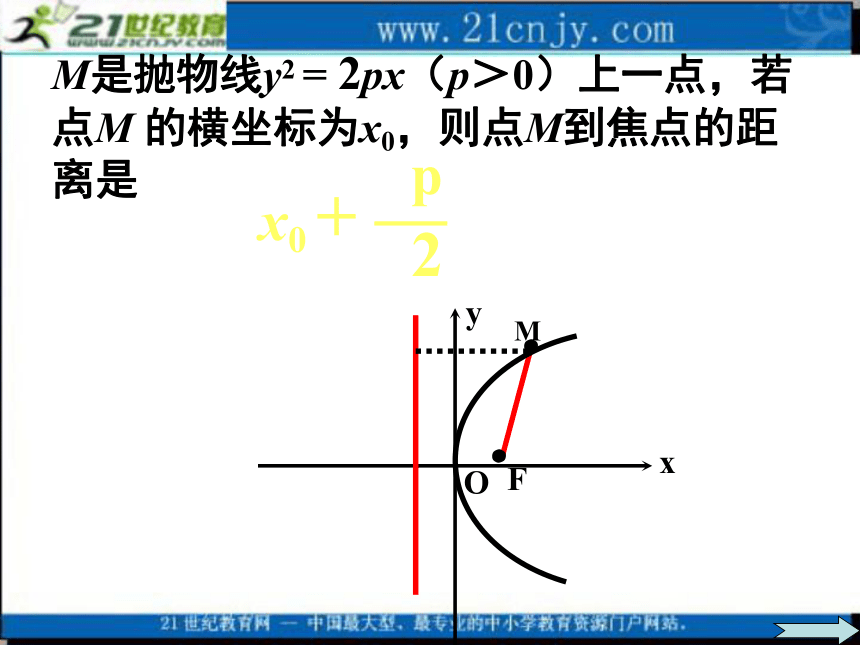
课件34张PPT。抛物线的简单几何性质(一)M是抛物线y2 = 2px(p>0)上一点,若点M 的横坐标为x0,则点M到焦点的距离是.焦半径及焦半径公式抛物线上一点到焦点的距离P(x0,y0)在y2=2px上,
P(x0,y0)在y2=-2px上,
P(x0,y0)在x2=2py上,
P(x0,y0)在x2=-2py上,
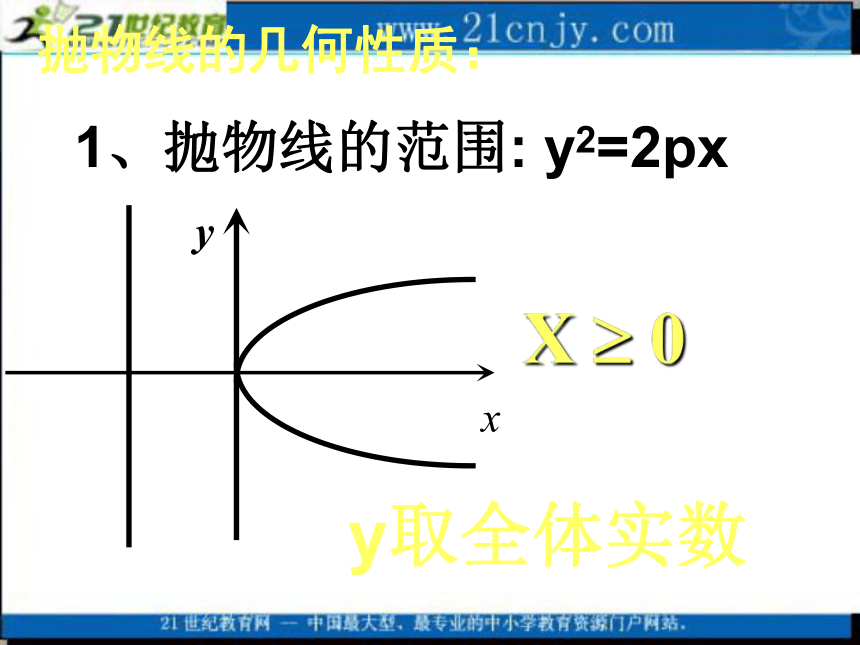
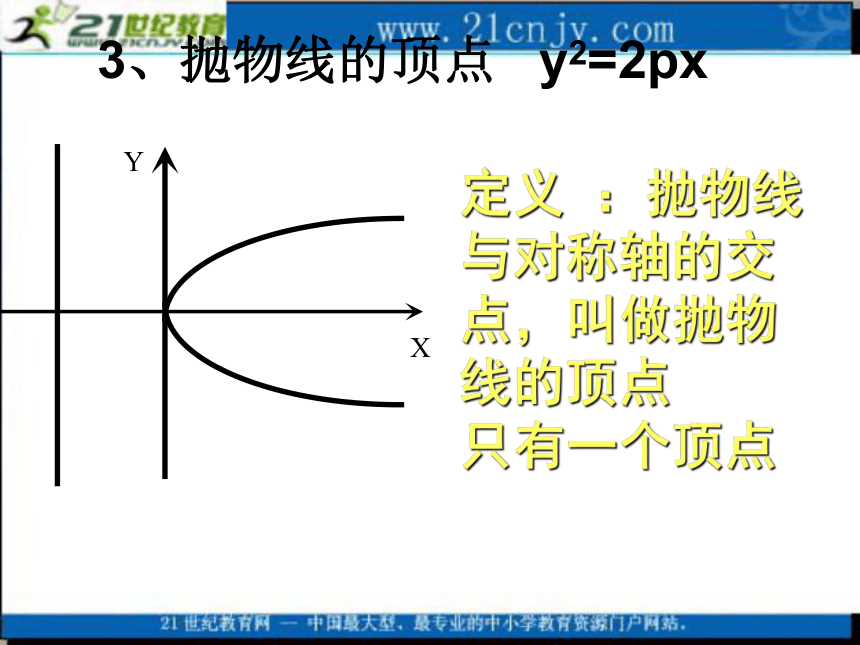
1、抛物线的范围: y2=2pxy取全体实数X ? 0抛物线的几何性质:2、抛物线的对称性 y2=2px关于x轴对称没有对称中心,因此,抛物线又叫做无心圆锥曲线。 而椭圆和双曲线又叫做有心圆锥曲线 定义 :抛物线与对称轴的交点,叫做抛物线的顶点
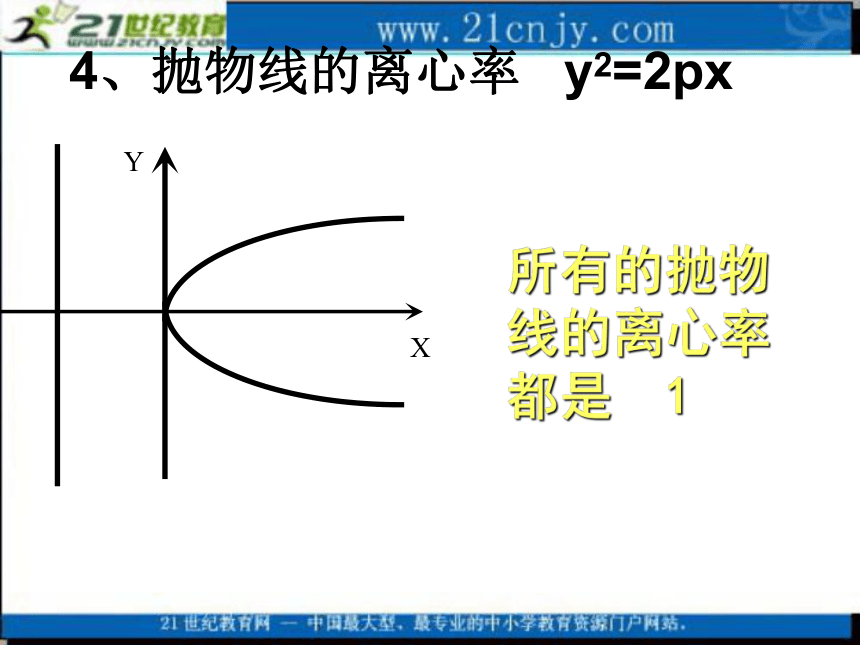
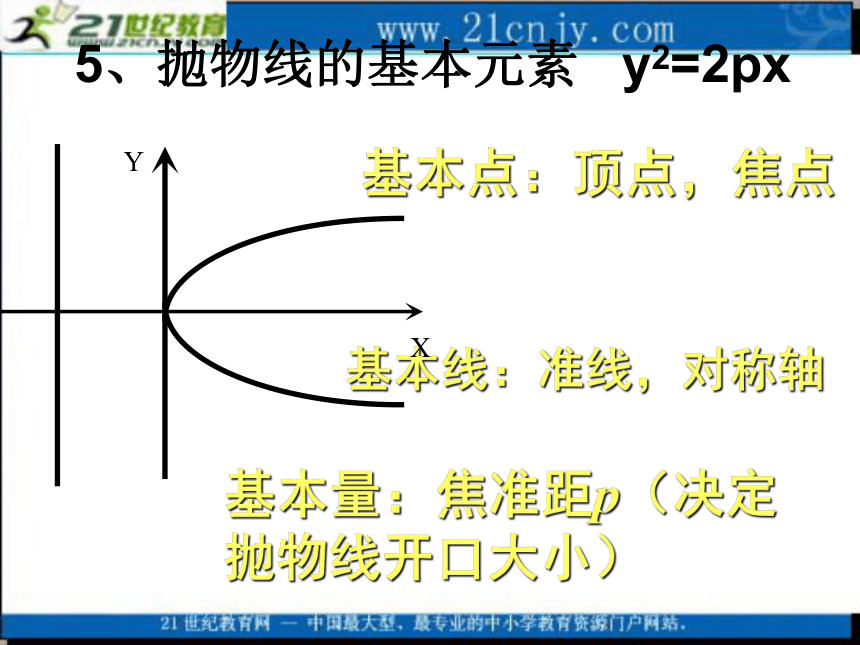
只有一个顶点 3、抛物线的顶点 y2=2px所有的抛物线的离心率都是 14、抛物线的离心率 y2=2px基本点:顶点,焦点基本线:准线,对称轴基本量:焦准距p(决定抛物线开口大小) 5、抛物线的基本元素 y2=2px例1:已知抛物线y2=2x
(1)设点A的坐标为( ,0),求曲
线上与点A距离最近的点P的坐标及相应的|PA|的值;(2)若上题中A(2,0),则结果如何?例2: 斜率为1的直线经过抛物线y2 =4x 的焦点,与抛物线相交于两点A、B, 求线段AB的长.6、焦点弦和通径通径是焦点弦中最短的弦,
通径|AB|=2p设AB是抛物线y2=2px(p>0)过焦点F
的一条弦。设A(x1,y1),B(x2,y2),AB的
中点M(x0,y0),过A,B,M分别向抛物线
的准线作垂线,垂足为A1,B1,M1,则
A(x1,y1)(1)|AB|=x1+x2+p (2)x1x2= ,y1y2= - p2(5)证明:以AB为直径的圆与准线相切y2=2px(p>0)∠AM1B=Rt ∠,
∠A1FB1=Rt ∠N练习1:
已知抛物线方程为y2=4x,直线l过定点P(-2,1),斜率为k.则k为何值时,直线l与抛物线y2=4x 只有一个公共点;有两个公共点;没有公共点呢。提出问题 过抛物线 的焦点的一条直线和抛物线相交,两交点的纵坐标为 ,
求证: .(焦点弦的其中
一条性质) 探究1 过焦点的直线具有上述性质,反之,若直线AB与抛物线 的两个交点A,B的纵坐标为 ,且 ,那么直线AB是否经过焦点F 呢? 探究2 既然过抛物线焦点的直线与其相交,交点的纵坐标的乘积是一个定值,那么过抛物线对称轴上其他任意一定点,是否也有这个性质呢?探究3 设抛物线 上两动点
,且满足
,问AB是否恒过某一定点? 探究4 设抛物线 上两动点
,且满足
,求AB中点P的轨迹方程.探究5 设抛物线 上两动点
,O为坐标原点,
OA⊥OB,则直线AB是否过定点?求AB中点P的轨迹方程.探究6 设抛物线 上两动点
,M为该抛物线上一定点,且MA⊥MB,则直线AB是否过定点?探究7 若M为抛物线 上一个定点,A、B是抛物线上的两个动点,且 (r为非零常数),求证:直线AB过定点。 将“探究6”的 “直线MA与直线MB的倾斜角之差为900”变为“直线MA与直线MB的倾斜角之和为900”,即 ,r =1,直线AB过定点.将“探究6”的 “直线MA与直线MB的倾斜角之差为900”变为“直线MA与直线MB的倾斜角之和为1800”,直线AB不过定点,但可得到: 探究8 若M为抛物线 上一个定点,A、B是抛物线上的两个动点,且直线MA与直线MB的倾斜角互补,求证:直线AB的斜率为定值。 设计意图:培养学生研究数学问题的一般思想方法,一是考虑原命题的逆命题是否成立;二是考虑能否把原命题进行一般推广;三是考虑从原命题条件中还能推出什么结论?四是考虑把原命题进行适当变式进行拓展。 问题 (2004年北京卷理)
过抛物线 上一定点
,作两条直线分别交抛物线于 .当PA与PB的斜率存在且倾斜角互补时,求 的值,并证明直线AB的斜
率为非零常数.变式1过抛物线 上一定点 ,作两条直线分别交抛物线于 ,若直线AB的斜率为定值 ,证明直线PA与PB的倾斜角互补. 设动直线AB:y=-x+b与抛物线 相交于两点 ,问在直线MN:x=2上能否找到一定点P(坐标与b 的值无关),使得直线PA与PB的倾斜角互补?变式2变式3 如图,抛物线 ,
过点P(1,0)作斜率为k的直线l交抛物线于A、B两点,A关于x轴的对称点为C,直线BC交x轴于Q点,当k变化时,探究点Q是否为定点?练习1:
如图,定长为3的线段AB的两端点在抛物线y2=x上移动,设线段AB的中点为M,求点M到y轴的最短距离。练习2:正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个三角形的边长。变式:已知在抛物线y=x2上三个点A、B、C组成一个等腰直角三角形,且顶点B是直角顶点,
(1)设直线BC的斜率为k,求顶点B的坐标;
(2)求等腰直角三角形的面积的最小值。抛物线的对称性问题
例.已知直线过原点,抛物线的顶点在原点,焦点在x轴的正半轴上,且点A(-1,0)和B(0,8)关于直线的对称点都在抛物线上,求直线和抛物线的方程。
P(x0,y0)在y2=-2px上,
P(x0,y0)在x2=2py上,
P(x0,y0)在x2=-2py上,
1、抛物线的范围: y2=2pxy取全体实数X ? 0抛物线的几何性质:2、抛物线的对称性 y2=2px关于x轴对称没有对称中心,因此,抛物线又叫做无心圆锥曲线。 而椭圆和双曲线又叫做有心圆锥曲线 定义 :抛物线与对称轴的交点,叫做抛物线的顶点
只有一个顶点 3、抛物线的顶点 y2=2px所有的抛物线的离心率都是 14、抛物线的离心率 y2=2px基本点:顶点,焦点基本线:准线,对称轴基本量:焦准距p(决定抛物线开口大小) 5、抛物线的基本元素 y2=2px例1:已知抛物线y2=2x
(1)设点A的坐标为( ,0),求曲
线上与点A距离最近的点P的坐标及相应的|PA|的值;(2)若上题中A(2,0),则结果如何?例2: 斜率为1的直线经过抛物线y2 =4x 的焦点,与抛物线相交于两点A、B, 求线段AB的长.6、焦点弦和通径通径是焦点弦中最短的弦,
通径|AB|=2p设AB是抛物线y2=2px(p>0)过焦点F
的一条弦。设A(x1,y1),B(x2,y2),AB的
中点M(x0,y0),过A,B,M分别向抛物线
的准线作垂线,垂足为A1,B1,M1,则
A(x1,y1)(1)|AB|=x1+x2+p (2)x1x2= ,y1y2= - p2(5)证明:以AB为直径的圆与准线相切y2=2px(p>0)∠AM1B=Rt ∠,
∠A1FB1=Rt ∠N练习1:
已知抛物线方程为y2=4x,直线l过定点P(-2,1),斜率为k.则k为何值时,直线l与抛物线y2=4x 只有一个公共点;有两个公共点;没有公共点呢。提出问题 过抛物线 的焦点的一条直线和抛物线相交,两交点的纵坐标为 ,
求证: .(焦点弦的其中
一条性质) 探究1 过焦点的直线具有上述性质,反之,若直线AB与抛物线 的两个交点A,B的纵坐标为 ,且 ,那么直线AB是否经过焦点F 呢? 探究2 既然过抛物线焦点的直线与其相交,交点的纵坐标的乘积是一个定值,那么过抛物线对称轴上其他任意一定点,是否也有这个性质呢?探究3 设抛物线 上两动点
,且满足
,问AB是否恒过某一定点? 探究4 设抛物线 上两动点
,且满足
,求AB中点P的轨迹方程.探究5 设抛物线 上两动点
,O为坐标原点,
OA⊥OB,则直线AB是否过定点?求AB中点P的轨迹方程.探究6 设抛物线 上两动点
,M为该抛物线上一定点,且MA⊥MB,则直线AB是否过定点?探究7 若M为抛物线 上一个定点,A、B是抛物线上的两个动点,且 (r为非零常数),求证:直线AB过定点。 将“探究6”的 “直线MA与直线MB的倾斜角之差为900”变为“直线MA与直线MB的倾斜角之和为900”,即 ,r =1,直线AB过定点.将“探究6”的 “直线MA与直线MB的倾斜角之差为900”变为“直线MA与直线MB的倾斜角之和为1800”,直线AB不过定点,但可得到: 探究8 若M为抛物线 上一个定点,A、B是抛物线上的两个动点,且直线MA与直线MB的倾斜角互补,求证:直线AB的斜率为定值。 设计意图:培养学生研究数学问题的一般思想方法,一是考虑原命题的逆命题是否成立;二是考虑能否把原命题进行一般推广;三是考虑从原命题条件中还能推出什么结论?四是考虑把原命题进行适当变式进行拓展。 问题 (2004年北京卷理)
过抛物线 上一定点
,作两条直线分别交抛物线于 .当PA与PB的斜率存在且倾斜角互补时,求 的值,并证明直线AB的斜
率为非零常数.变式1过抛物线 上一定点 ,作两条直线分别交抛物线于 ,若直线AB的斜率为定值 ,证明直线PA与PB的倾斜角互补. 设动直线AB:y=-x+b与抛物线 相交于两点 ,问在直线MN:x=2上能否找到一定点P(坐标与b 的值无关),使得直线PA与PB的倾斜角互补?变式2变式3 如图,抛物线 ,
过点P(1,0)作斜率为k的直线l交抛物线于A、B两点,A关于x轴的对称点为C,直线BC交x轴于Q点,当k变化时,探究点Q是否为定点?练习1:
如图,定长为3的线段AB的两端点在抛物线y2=x上移动,设线段AB的中点为M,求点M到y轴的最短距离。练习2:正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个三角形的边长。变式:已知在抛物线y=x2上三个点A、B、C组成一个等腰直角三角形,且顶点B是直角顶点,
(1)设直线BC的斜率为k,求顶点B的坐标;
(2)求等腰直角三角形的面积的最小值。抛物线的对称性问题
例.已知直线过原点,抛物线的顶点在原点,焦点在x轴的正半轴上,且点A(-1,0)和B(0,8)关于直线的对称点都在抛物线上,求直线和抛物线的方程。
