11.2.5 三角形全等的条件5 HL
文档属性
| 名称 | 11.2.5 三角形全等的条件5 HL |  | |
| 格式 | rar | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-17 13:17:00 | ||
图片预览

文档简介
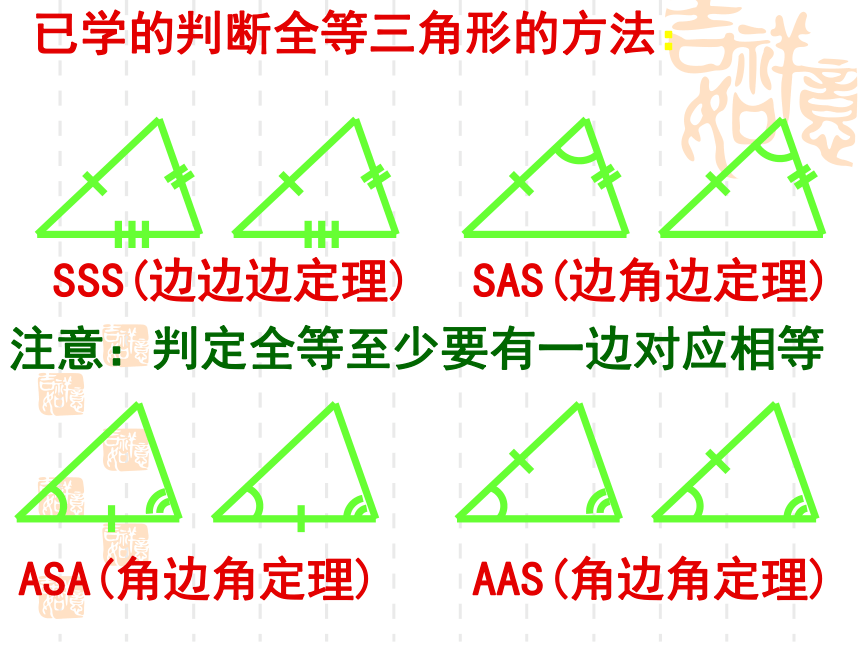
课件14张PPT。直角三角形全等判定已学的判断全等三角形的方法:SSS(边边边定理)SAS(边角边定理)ASA(角边角定理)AAS(角边角定理)注意:判定全等至少要有一边对应相等
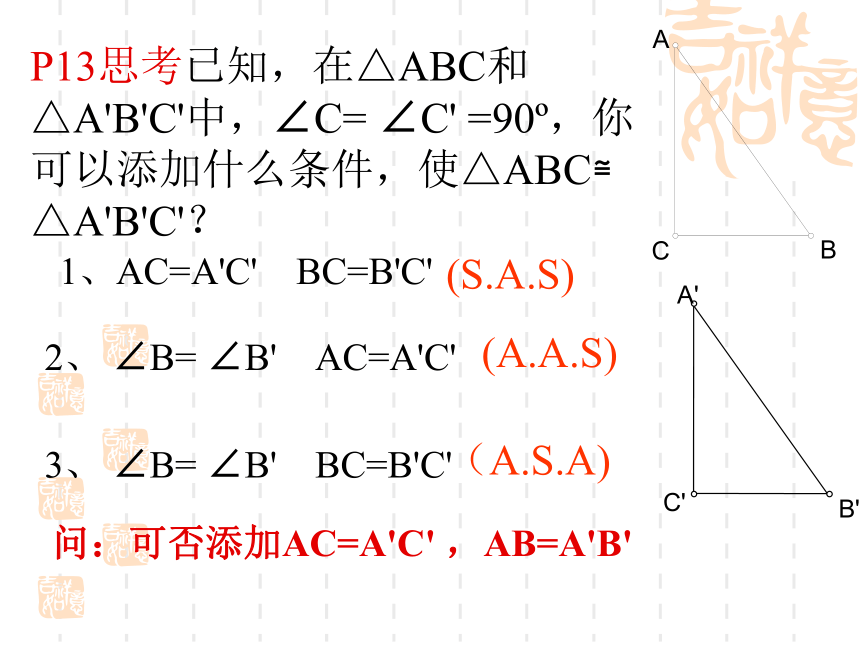
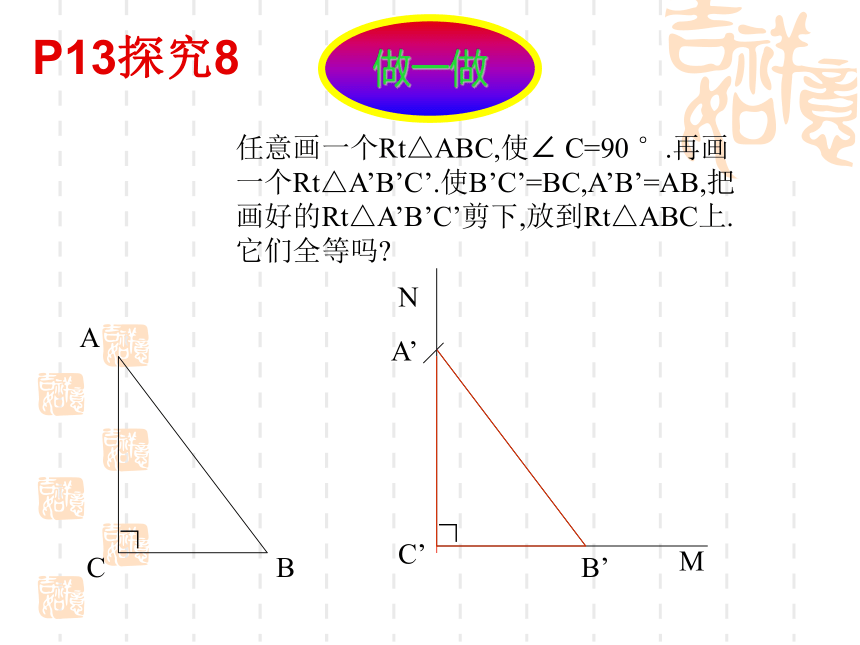
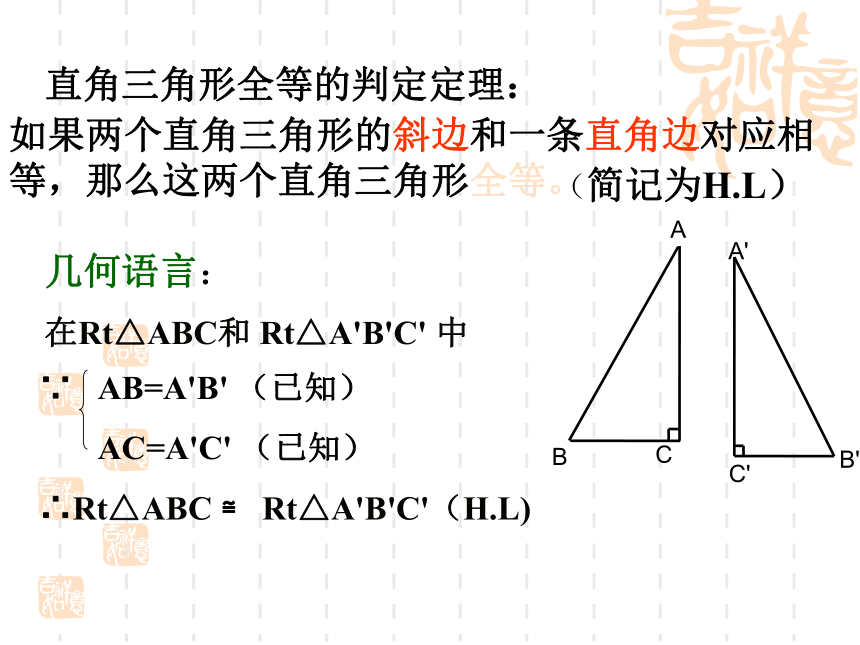
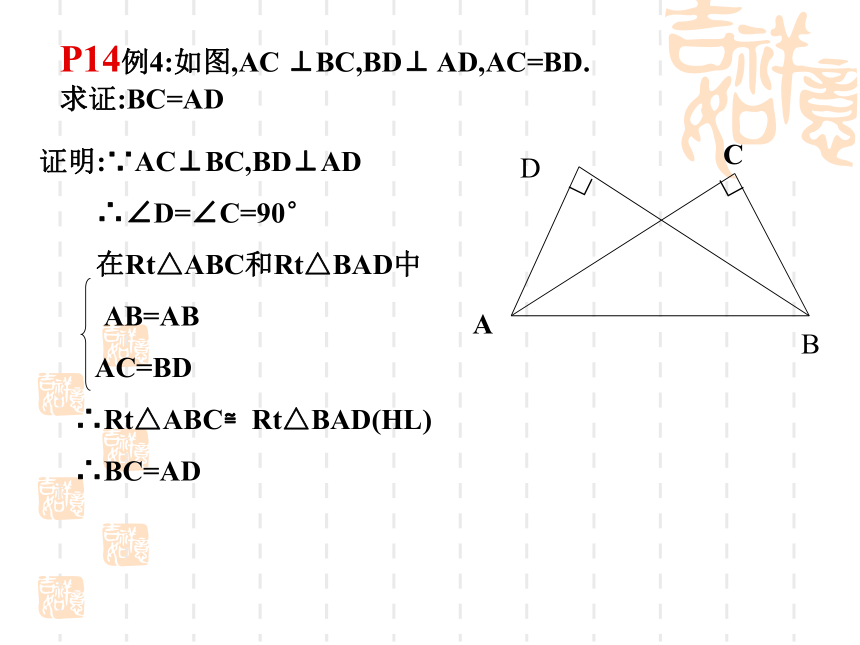
P13思考已知,在△ABC和△A'B'C'中,∠C= ∠C' =90o,你可以添加什么条件,使△ABC≌ △A'B'C'?1、AC=A'C' BC=B'C' (S.A.S)2、 ∠B= ∠B' AC=A'C'(A.A.S)3、 ∠B= ∠B' BC=B'C' (A.S.A)问:可否添加AC=A'C' ,AB=A'B'做一做任意画一个Rt△ABC,使∠ C=90 °.再画一个Rt△A’B’C’.使B’C’=BC,A’B’=AB,把画好的Rt△A’B’C’剪下,放到Rt△ABC上.它们全等吗?∟A’∟C’MNABCB’P13探究8直角三角形全等的判定定理:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。(简记为H.L)几何语言:在Rt△ABC和 Rt△A'B'C' 中P14例4:如图,AC ⊥BC,BD⊥ AD,AC=BD.求证:BC=AD∟∟ABC证明:∵AC⊥BC,BD⊥AD
∴∠D=∠C=90°
在Rt△ABC和Rt△BAD中
AB=AB
AC=BD
∴Rt△ABC≌Rt△BAD(HL)
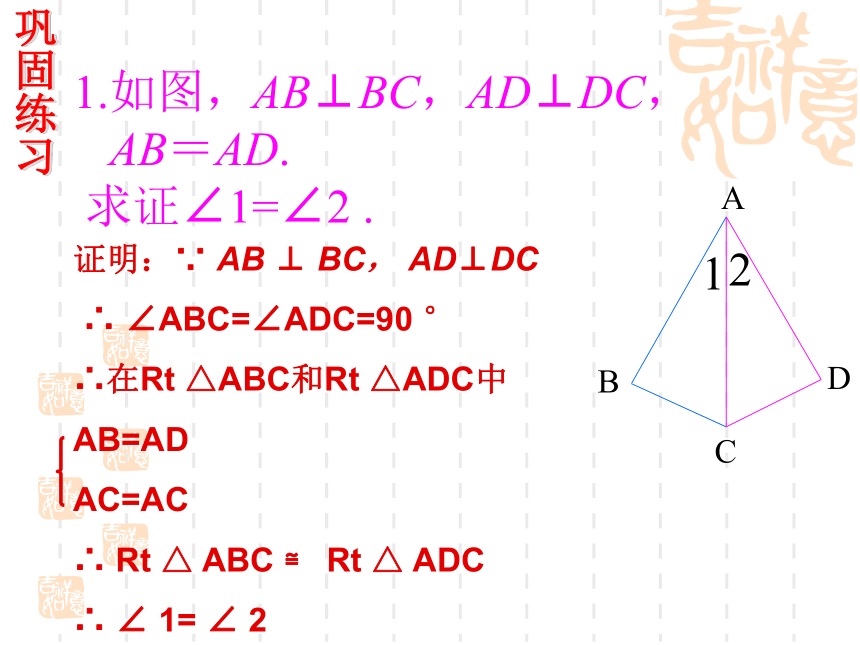
∴BC=ADD1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .巩固练习证明:∵ AB ⊥ BC, AD⊥DC
∴ ∠ABC=∠ADC=90 °
∴在Rt △ABC和Rt △ADC中
AB=AD
AC=AC
∴ Rt △ ABC ≌ Rt △ ADC
∴ ∠ 1= ∠ 2巩固练习P14 1.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?解:DA=EB
理由:∵C为AB中点
∴AC=BC,且CD=CE
又∵ DA⊥AB, EB⊥AB
∴ ∠CAD=∠CBE=90 °
∴在Rt △ACD和Rt △BCE中
CD=CE
AC=BC
∴ Rt △ACD ≌ Rt △BCE
∴ DA=EB
巩固练习P14 2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.证明: ∵ CE=BF
∴ CE-EF=BF-EF 即CF=BE
又∵ AE⊥BC, DF⊥BC
∴ ∠CFD=∠BEA=90 °
∴在Rt △CFD和Rt △BEA中
CD=AB
CF=BE
∴ Rt △CFD≌ Rt △BEA
∴ AE=DF
练一练如图,D为BC边上的中点,DE⊥AB
DF ⊥AC,且DE=DF,
那么△DBE≌ △DCF吗?证明:∵DE⊥AB,DF⊥AC,
∴△DBE和△DCF为Rt△,
∵D为BC边的中点,
∴BD=CD,
在Rt△DBE和Rt△DCF中
DE=DF
BD=CD
∴Rt△DBE≌Rt△DCF(HL)
即△DBE≌△DCF 如下 图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么数量关系?议一议∠ABC+∠DFE=90°.证明:在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (H.L).∴∠ABC=∠DEF
(全等三角形对应角相等).又 ∠DEF+∠DFE=180°–90°=90°∴∠ABC+∠DFE=90°(等量代换)1. 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“H.L”.2. 两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只须找两个条件(两个条件中至少有一个条件是一对对应边相等).通过这节课的学习你有何收获?作业:1、课本习题13.2—7.8.12题
2、思考:已知一个角∠AOB,你能否只用一块三角板画出∠AOB的角平分线?说出画法和理由.
P13思考已知,在△ABC和△A'B'C'中,∠C= ∠C' =90o,你可以添加什么条件,使△ABC≌ △A'B'C'?1、AC=A'C' BC=B'C' (S.A.S)2、 ∠B= ∠B' AC=A'C'(A.A.S)3、 ∠B= ∠B' BC=B'C' (A.S.A)问:可否添加AC=A'C' ,AB=A'B'做一做任意画一个Rt△ABC,使∠ C=90 °.再画一个Rt△A’B’C’.使B’C’=BC,A’B’=AB,把画好的Rt△A’B’C’剪下,放到Rt△ABC上.它们全等吗?∟A’∟C’MNABCB’P13探究8直角三角形全等的判定定理:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。(简记为H.L)几何语言:在Rt△ABC和 Rt△A'B'C' 中P14例4:如图,AC ⊥BC,BD⊥ AD,AC=BD.求证:BC=AD∟∟ABC证明:∵AC⊥BC,BD⊥AD
∴∠D=∠C=90°
在Rt△ABC和Rt△BAD中
AB=AB
AC=BD
∴Rt△ABC≌Rt△BAD(HL)
∴BC=ADD1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .巩固练习证明:∵ AB ⊥ BC, AD⊥DC
∴ ∠ABC=∠ADC=90 °
∴在Rt △ABC和Rt △ADC中
AB=AD
AC=AC
∴ Rt △ ABC ≌ Rt △ ADC
∴ ∠ 1= ∠ 2巩固练习P14 1.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?解:DA=EB
理由:∵C为AB中点
∴AC=BC,且CD=CE
又∵ DA⊥AB, EB⊥AB
∴ ∠CAD=∠CBE=90 °
∴在Rt △ACD和Rt △BCE中
CD=CE
AC=BC
∴ Rt △ACD ≌ Rt △BCE
∴ DA=EB
巩固练习P14 2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.证明: ∵ CE=BF
∴ CE-EF=BF-EF 即CF=BE
又∵ AE⊥BC, DF⊥BC
∴ ∠CFD=∠BEA=90 °
∴在Rt △CFD和Rt △BEA中
CD=AB
CF=BE
∴ Rt △CFD≌ Rt △BEA
∴ AE=DF
练一练如图,D为BC边上的中点,DE⊥AB
DF ⊥AC,且DE=DF,
那么△DBE≌ △DCF吗?证明:∵DE⊥AB,DF⊥AC,
∴△DBE和△DCF为Rt△,
∵D为BC边的中点,
∴BD=CD,
在Rt△DBE和Rt△DCF中
DE=DF
BD=CD
∴Rt△DBE≌Rt△DCF(HL)
即△DBE≌△DCF 如下 图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么数量关系?议一议∠ABC+∠DFE=90°.证明:在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (H.L).∴∠ABC=∠DEF
(全等三角形对应角相等).又 ∠DEF+∠DFE=180°–90°=90°∴∠ABC+∠DFE=90°(等量代换)1. 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“H.L”.2. 两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只须找两个条件(两个条件中至少有一个条件是一对对应边相等).通过这节课的学习你有何收获?作业:1、课本习题13.2—7.8.12题
2、思考:已知一个角∠AOB,你能否只用一块三角板画出∠AOB的角平分线?说出画法和理由.
