3.6三角形、梯形的中位线

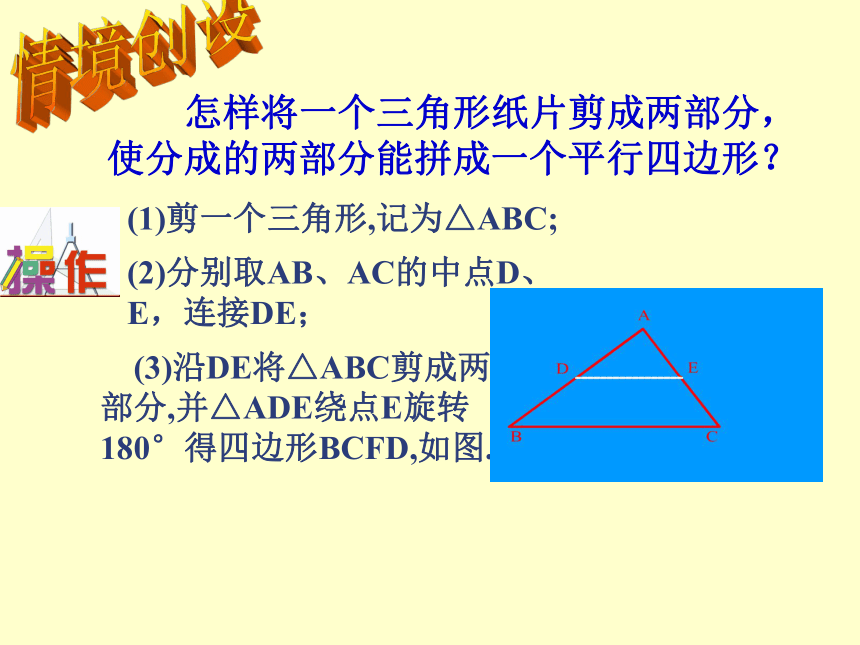
课件23张PPT。苏科版八年级数学3.6三角形、梯形的中位线(一)学习目标：１、探索并掌握三角形中位线的概念、性质;2、会利用三角形中位线的性质解决有关问题;3、经历探索三角形中位线的性质的过程，体会转化的思想。 怎样将一个三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？(1)剪一个三角形,记为△ABC;(2)分别取AB、AC的中点D、E，连接DE； (3)沿DE将△ABC剪成两部分,并△ADE绕点E旋转180°得四边形BCFD,如图. 情境创设四边形BCFD是平行四边形吗?为什么？四边形BCFD是平行四边形. 由中心对称的性质，知FC=AD，∠CFE= ∠ADE. 又由∠CFE= ∠ADE， 得AB∥FC；由DB=AD得DB=FC.所以四边形BCFD是平行四边形.DEBCAF三角形中位线的定义
连接三角形两边中点的线段叫做
三角形的中位线 。CABD E
1、画出△ABC，作出它的所有中位线，
并指出一个三角形有几条中位线。
2、在上图中作出三角形的三条中线，并
说明中线和中位线有何不同。
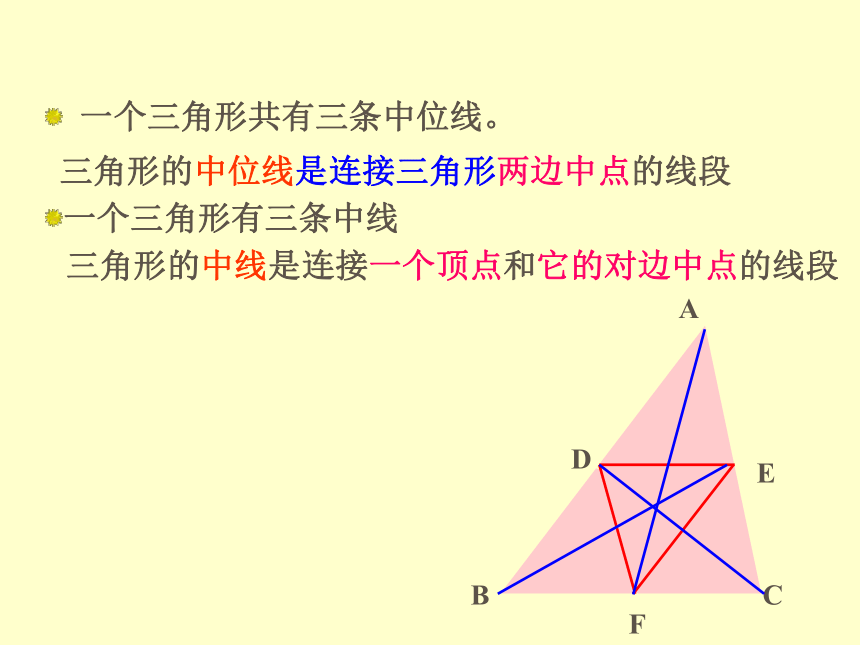
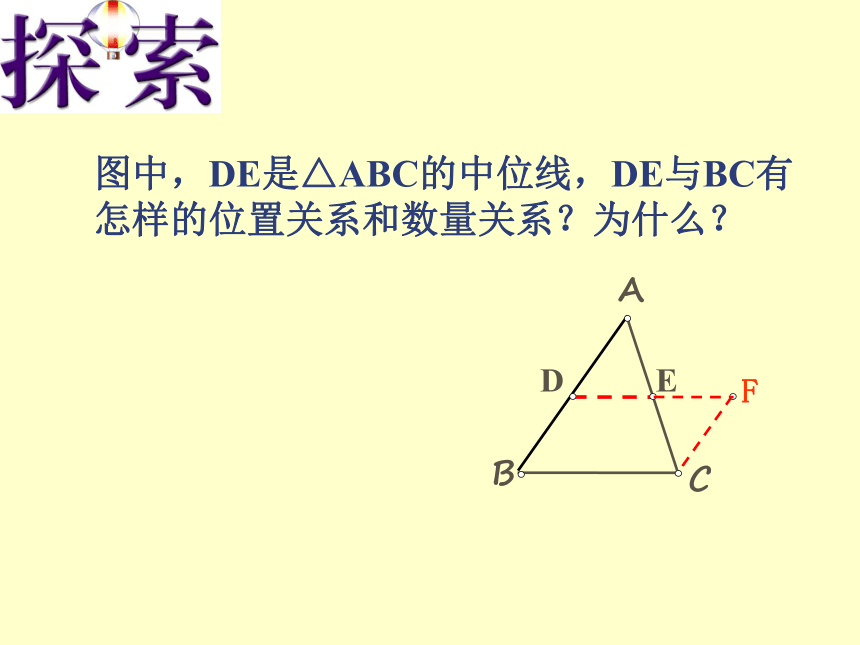
三角形的中位线是连接三角形两边中点的线段三角形的中线是连接一个顶点和它的对边中点的线段一个三角形有三条中线 一个三角形共有三条中位线。定义ABCD。E。F图中，DE是△ABC的中位线，DE与BC有怎样的位置关系和数量关系？为什么？ CEFBCD EA三角形的中位线平行于第三边，并且等于它的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC，
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途CCABD E 已知:三角形的各边分别为6cm,8cm, 10cm，则连接各边中点所成三角形的周长为 cm.12随着学习的不断深入，同学们将会有更多的办法来解决这个问题 如图，A、B两地被建筑物阻隔，为测量 A、B两地间的距离，在地面上选一点C，连接CA和CB，分别取CA和CB的中点D、E。
⑴若DE的长为36m，求A、B两地间的距离；⑵如果D、E两点间还有阻隔，你有什么解决的办法？36m如图，在四边形ABCD中，E、F、G 、H 分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗？为什么？
分析：已知
四边形EFGH
是平行四边形已知
EF ∥ AC
HG ∥AC EF ∥ HG
EH ∥FG四边形EFGH
是平行四边形方法一：方法二：（同理）解：四边形EFGH是平行四边形连接AC在△ABC中,因为E、F分别是AB 、BC的中点，即EF是△ABC的中位线，所以EF ∥ AC， EF =1/2AC理由是：三角形的中位线平行于第三边，并且等于它的一半。在△ADC中，同样可以得到HG∥ AC， HG =1/2 AC所以EF ∥ HG， EF =HG
所以四边形EFGH是平行四边形
理由是：一组对边平行并且相等的四边形是平行四边形
变题1、若四边形ABCD从普通形状变成平行四边形，其它条件不变，则四边形EFGH的形状会变化吗？为什么？ 变题2、若四边形ABCD从普通的四边形变成矩形，其它条件不变，则四边形EFGH的形状会变化吗？为什么？ 变题3、若四边形ABCD从普通的四边形变成菱形，其它条件不变，则四边形EFGH的形状会有变化吗？为什么？ 变题4、若四边形ABCD从普通四边形变成正方形，其它的条件不变，则四边形EFGH的形状会有变化吗？为什么？ 如图: △ABC的中线AF与中位线DE相交于O点,AF与DE有怎样的关系?为什么?
CABD E oF 这节课，你有什么收获？
数学是思维的体操!勇于尝试,我们就能成就更多，学到更多! ——与同学们共勉作业:P134.习题3.6 第1题 再见请多提宝贵意见