平行线及其判定
图片预览









文档简介
课件37张PPT。5.2 平行线及其判定
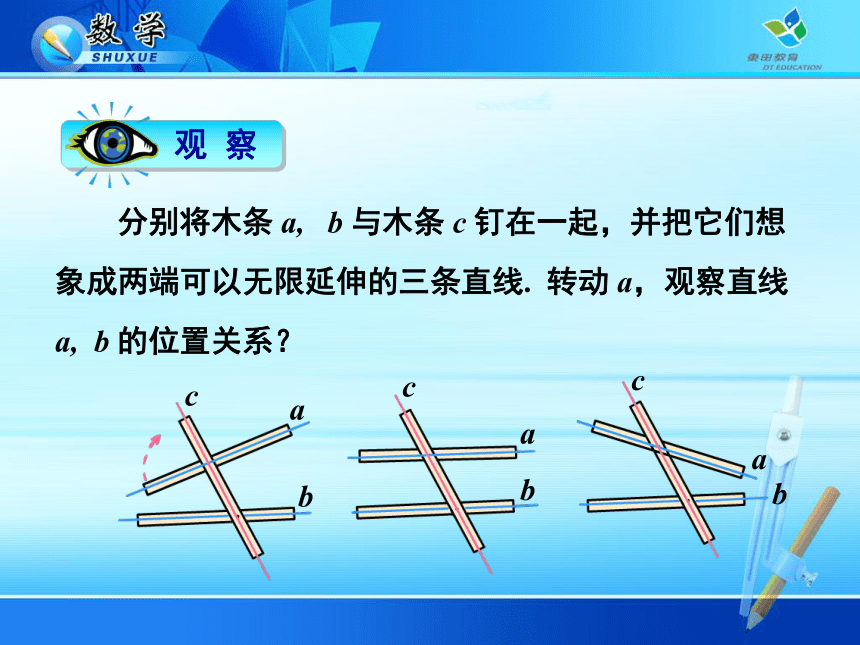
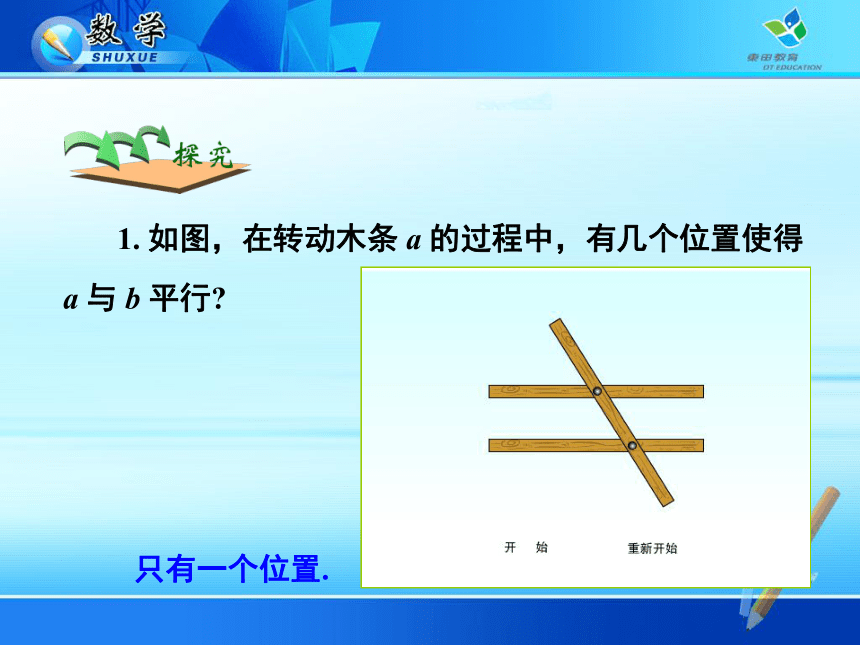
5.2.1 平行线 分别将木条 a, b 与木条 c 钉在一起,并把它们想象成两端可以无限延伸的三条直线. 转动 a,观察直线 a, b 的位置关系? 在同一平面内,若直线 a 与直线 b 不相交,那么就称直线 a 与 b 平行,记作 a∥b.你能举出生活中有关平行的例子吗? 1. 如图,在转动木条 a 的过程中,有几个位置使得
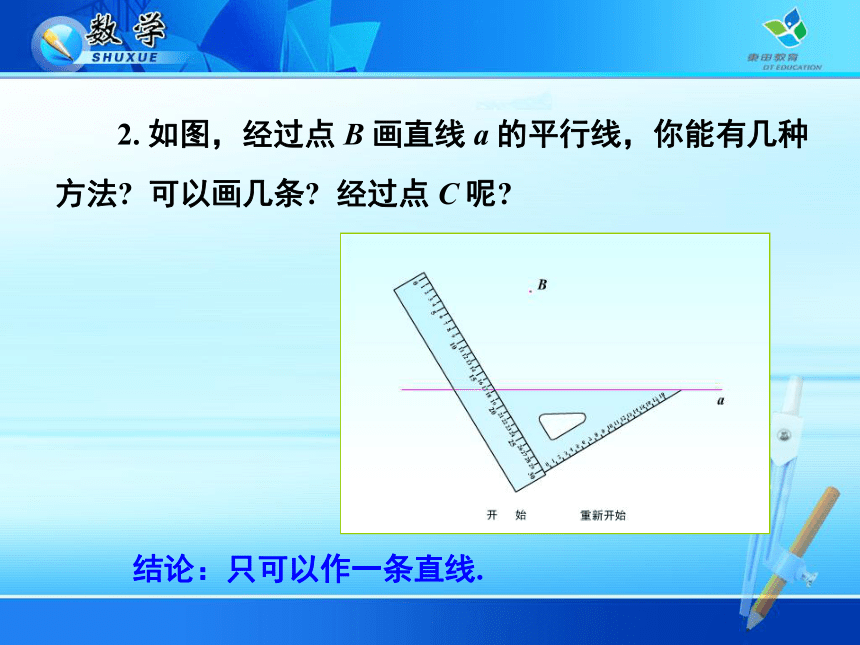
a 与 b 平行?只有一个位置. 2. 如图,经过点 B 画直线 a 的平行线,你能有几种方法? 可以画几条? 经过点 C 呢?CB a 2. 如图,经过点 B 画直线 a 的平行线,你能有几种方法? 可以画几条? 经过点 C 呢?结论:只可以作一条直线.1. 经过上述问题的解决,你能得到什么结论?
经过直线外一点,有且只有一条直线与这条直线平行. 2. 如图,若 a∥b,b∥c,你能得到 a∥c 吗?说明
你的理由?从中你能得到什么? 解:假设 a 与 c 不平行,则可以设 a 与 c 相交于点
O,又因为 a∥b,b∥c,于是过点O 有两条直线 a 和 c
都与 b 平行,这与平行公理矛盾. 所以假设不正确,因此 a 和 c 一定平行.
即如果两条直线都与第三
条直线平行,那么这两条直线
也互相平行. 1. 如图,AD∥BC,在 AB 上取一点 M,过点 M 作 MN∥BC,且交 CD 于点 N. 说明 MN 与 AD 的位置关系,为什么? 解:因为 AD∥BC,MN∥BC,
根据平行于同一直线的两直线
平行,可以得到 MN∥AD. 2. 在同一平面内有 4 条直线,这 4 条直线可以把这个平面分成几部分? (2) 当 4 条直线中只有三条直线两两平行时,可以把平面分成 8 部分. (3) 当 4 条直线仅有两条直线互相平行时,可以把整个平面分成 9 部分或 10 部分. (4) 当 4 条直线中有两条直线平行,另两条直线也平行时,可以把平面分成 9 部分. (5) 当 4 条直线任意两条都不平行时,可以把平面
分成 8 部分, 或 10 部分, 或 11 部分. 1. 平行线的定义;
2. 平行公理及其推论;
3. 平行公理及推论的应用 —— 利用其可以说明两条直线的位置关系.5.2.2 平行线的判定 1. 如图,三根木条相交成∠1,∠2,固定木条 b, c,转动木条 a . 在这个过程中,∠1 和∠2 的大小发生变化,∠1,∠2 的位置关系是否发生了变化?你能描述∠1,∠2 的位置特征吗? 结论:∠1,∠2 的位置关系没有发生变化.
同位角:∠1,∠2 在截线的同侧,在被截直线的同方向,那么称∠1 和∠2 是同位角. 2. 如图,三根木条相交成∠1,∠2,固定木条 b, c,转动木条 a. ∠1 和∠2 的大小发生变化,在这个过
程中,∠1,∠2 的位置关系是否发生了变化?你能描
述∠1,∠2 的位置特征吗? 结论:∠1,∠2 的位置关系没有发生变化.
内错角:∠1,∠2 在截线的两侧,在被截直线之间,那么称∠1 和∠2 是内错角. 3. 三根木条相交成∠1,∠2,固定木条 b, c,转
动木条 a. ∠1 和∠2 的大小发生变化,在这个过程中,∠1,∠2 的位置关系是否发生了变化?你能描述∠1,∠2 的位置特征吗? 结论:∠1,∠2 的位置关系没有发生变化.
同旁内角:∠1,∠2 在截线的同旁,在被截直线之间,那么称∠1 和∠2 是同旁内角. 用三角板和直尺过直线 AB 外一点 C 作 AB 的平行线,从中你发现了什么? 平行线的判定定理:
两条直线被第三条直线所截,若同位角相等,则这两条直线平行. 即同位角相等,两直线平行.
符号语言:如图,若∠1 =∠2,则 AB∥CD. 1. 内错角满足什么关系时,两直线平行?
如图,若∠1 =∠2,又∠1 =∠3 , 于是∠2 =∠3. 根据同位角相等,两直线平行得到若∠1 =∠2,则AB∥CD. 2. 同旁内角满足什么关系时,两直线平行?
如图,若∠1 +∠2 = 180o,有∠1 +∠3 = 180o,根
据同角的补角相等,可以得到 ∠3 = ∠2. 根据同位角
相等,两直线平行可以得到 AB∥CD.直线平行的条件:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.1. 如图,若 a⊥b,a⊥c,b 与 c 平行吗?为什么?解: 因为 a⊥b,a⊥c,
所以∠1 =∠2 = 90o.
所以 b∥c.垂直于同一条直线的两条直线平行. 2. 如图,直线 AB, CD 被 EF 所截. 若∠1 +∠2 = 180o, ∠2 +∠3 = 180o ,那么 AB 与 CD 平行吗? 为什么? 解: 因为∠1 +∠2 = 180o,
∠2 +∠3 = 180o,
所以∠1 = ∠3.
所以 AB∥CD. 3. 如图,若∠B +∠D =∠BED,那么 AB 与 CD 平行吗?为什么? 分析: 通过条件∠B +∠D =∠BED 可以发现,要想
说明 AB∥CD,必须构造三类角,找到三类角的关系即可. 但此时没有三类角,于是可以想到构造三类角. 例如,过点 E 作∠BEF =∠B,又因为 ∠B +∠D =∠BED,可以得到∠D =∠FED. 根据内错角相等, 两直
线平行可以得到 AB∥EF, CD∥EF,再根据平行公理的推论,可以得到 AB∥CD.F 1. 同位角、内错角和同旁内角的概念;
2. 直线平行的条件:由三类角的数量关系得到直线平行的条件.
5.2.1 平行线 分别将木条 a, b 与木条 c 钉在一起,并把它们想象成两端可以无限延伸的三条直线. 转动 a,观察直线 a, b 的位置关系? 在同一平面内,若直线 a 与直线 b 不相交,那么就称直线 a 与 b 平行,记作 a∥b.你能举出生活中有关平行的例子吗? 1. 如图,在转动木条 a 的过程中,有几个位置使得
a 与 b 平行?只有一个位置. 2. 如图,经过点 B 画直线 a 的平行线,你能有几种方法? 可以画几条? 经过点 C 呢?CB a 2. 如图,经过点 B 画直线 a 的平行线,你能有几种方法? 可以画几条? 经过点 C 呢?结论:只可以作一条直线.1. 经过上述问题的解决,你能得到什么结论?
经过直线外一点,有且只有一条直线与这条直线平行. 2. 如图,若 a∥b,b∥c,你能得到 a∥c 吗?说明
你的理由?从中你能得到什么? 解:假设 a 与 c 不平行,则可以设 a 与 c 相交于点
O,又因为 a∥b,b∥c,于是过点O 有两条直线 a 和 c
都与 b 平行,这与平行公理矛盾. 所以假设不正确,因此 a 和 c 一定平行.
即如果两条直线都与第三
条直线平行,那么这两条直线
也互相平行. 1. 如图,AD∥BC,在 AB 上取一点 M,过点 M 作 MN∥BC,且交 CD 于点 N. 说明 MN 与 AD 的位置关系,为什么? 解:因为 AD∥BC,MN∥BC,
根据平行于同一直线的两直线
平行,可以得到 MN∥AD. 2. 在同一平面内有 4 条直线,这 4 条直线可以把这个平面分成几部分? (2) 当 4 条直线中只有三条直线两两平行时,可以把平面分成 8 部分. (3) 当 4 条直线仅有两条直线互相平行时,可以把整个平面分成 9 部分或 10 部分. (4) 当 4 条直线中有两条直线平行,另两条直线也平行时,可以把平面分成 9 部分. (5) 当 4 条直线任意两条都不平行时,可以把平面
分成 8 部分, 或 10 部分, 或 11 部分. 1. 平行线的定义;
2. 平行公理及其推论;
3. 平行公理及推论的应用 —— 利用其可以说明两条直线的位置关系.5.2.2 平行线的判定 1. 如图,三根木条相交成∠1,∠2,固定木条 b, c,转动木条 a . 在这个过程中,∠1 和∠2 的大小发生变化,∠1,∠2 的位置关系是否发生了变化?你能描述∠1,∠2 的位置特征吗? 结论:∠1,∠2 的位置关系没有发生变化.
同位角:∠1,∠2 在截线的同侧,在被截直线的同方向,那么称∠1 和∠2 是同位角. 2. 如图,三根木条相交成∠1,∠2,固定木条 b, c,转动木条 a. ∠1 和∠2 的大小发生变化,在这个过
程中,∠1,∠2 的位置关系是否发生了变化?你能描
述∠1,∠2 的位置特征吗? 结论:∠1,∠2 的位置关系没有发生变化.
内错角:∠1,∠2 在截线的两侧,在被截直线之间,那么称∠1 和∠2 是内错角. 3. 三根木条相交成∠1,∠2,固定木条 b, c,转
动木条 a. ∠1 和∠2 的大小发生变化,在这个过程中,∠1,∠2 的位置关系是否发生了变化?你能描述∠1,∠2 的位置特征吗? 结论:∠1,∠2 的位置关系没有发生变化.
同旁内角:∠1,∠2 在截线的同旁,在被截直线之间,那么称∠1 和∠2 是同旁内角. 用三角板和直尺过直线 AB 外一点 C 作 AB 的平行线,从中你发现了什么? 平行线的判定定理:
两条直线被第三条直线所截,若同位角相等,则这两条直线平行. 即同位角相等,两直线平行.
符号语言:如图,若∠1 =∠2,则 AB∥CD. 1. 内错角满足什么关系时,两直线平行?
如图,若∠1 =∠2,又∠1 =∠3 , 于是∠2 =∠3. 根据同位角相等,两直线平行得到若∠1 =∠2,则AB∥CD. 2. 同旁内角满足什么关系时,两直线平行?
如图,若∠1 +∠2 = 180o,有∠1 +∠3 = 180o,根
据同角的补角相等,可以得到 ∠3 = ∠2. 根据同位角
相等,两直线平行可以得到 AB∥CD.直线平行的条件:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.1. 如图,若 a⊥b,a⊥c,b 与 c 平行吗?为什么?解: 因为 a⊥b,a⊥c,
所以∠1 =∠2 = 90o.
所以 b∥c.垂直于同一条直线的两条直线平行. 2. 如图,直线 AB, CD 被 EF 所截. 若∠1 +∠2 = 180o, ∠2 +∠3 = 180o ,那么 AB 与 CD 平行吗? 为什么? 解: 因为∠1 +∠2 = 180o,
∠2 +∠3 = 180o,
所以∠1 = ∠3.
所以 AB∥CD. 3. 如图,若∠B +∠D =∠BED,那么 AB 与 CD 平行吗?为什么? 分析: 通过条件∠B +∠D =∠BED 可以发现,要想
说明 AB∥CD,必须构造三类角,找到三类角的关系即可. 但此时没有三类角,于是可以想到构造三类角. 例如,过点 E 作∠BEF =∠B,又因为 ∠B +∠D =∠BED,可以得到∠D =∠FED. 根据内错角相等, 两直
线平行可以得到 AB∥EF, CD∥EF,再根据平行公理的推论,可以得到 AB∥CD.F 1. 同位角、内错角和同旁内角的概念;
2. 直线平行的条件:由三类角的数量关系得到直线平行的条件.
