第3课时 菱形概念、性质、判定
文档属性
| 名称 | 第3课时 菱形概念、性质、判定 |

|
|
| 格式 | rar | ||
| 文件大小 | 337.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-16 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第十九章 四边形
第11课时 菱形概念、性质、判定
通过本节的学习需要掌握菱形概念,知道菱形与平行四边形的关系.理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积.通过运用菱形知识解决具体问题,提高分析能力和观察能力.根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
点击一:定义:
定义:有一组邻边相等的平行四边形叫做菱形.
【强调】 菱形(1)是平行四边形;(2)一组邻边相等.
点击二:菱形的性质
(1)具有平行四边形的性质
(2)菱形的四条边相等
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
注意:(1)菱形是特殊的平行四边形,是中心对称图形,过中心的任意直线可将菱形分成完全全等的两部分(2)菱形也是轴对称图形,有两条对称轴,对称轴的交点就是对称中心
针对练习:
1.如图1,已知菱形ABCD的周长为16cm,∠ABC=120°,求对角线BD和AC的长.
解析:知道了菱形的周长可以求到菱形的边长,再根据菱形的性质可得到△ABD是等边三角形,这样可求得对角线BD的长,最后借助勾股定理求得AC的长.
解:在菱形ABCD中,AB+BC+CD+AD=16cm,∠ABC=120°.
∴AB=AD=BC=CD=4cm.
由对角线BD平分∠ABC,得∠ABD=60°.
∴△ABD是等边三角形,BD=AB=4cm.
∵菱形的对角线互相垂直平分,∴OB=2cm.
在Rt△AOB中,(cm).
∴(cm).
点击三:菱形的判定
(1)定义
(2)对角线互相垂直的平行四边形是菱形
(3)四条边相等的四边形是菱形
针对练习:
1.如图4,在△ABC中,AB=AC,AD是BC边上的高,过点D作DE∥AB交AC于点E,作DF∥AC交AB于点F,四边形AFDE是菱形吗?说说你的理由.
答案:先证四边形AFDE是平行四边形,再证邻边相等)
2. 如图2,的两条对角线AC、BD相交于点O,AB=10,AO=8,OB=6.
(1)AC、BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
解析:(1)要判断AC与BD是否垂直,可以根据已知条件,看△AOB是否是直角三角形,为此需要利用勾股定理的逆定理来解决;
(2)此问的解决是建立在(1)的基础上的,解决了(1),此问也就解决了.
解:在△ABO中,
∵AB=10,OA=8,OB=6,62+82=102,
∴OA2+OB2=AB2.
∴△ABO是直角三角形.
且∠AOB为直角.
∴ AC⊥BD.
(2)∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形.
点击四:菱形的面积公式
菱形的面积公式是 (其中a、b是菱形的两条对角线分别的长).即:“菱形的面积等于它的两条对角线长的积的一半”.当不易求出对角线长时,就用平行四边形面积的一般计算方法计算菱形面积S=底×高.
类型之一:菱形的性质
例1: 已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
证明:∵ 四边形ABCD是菱形,
∴ CB=CD, CA平分∠BCD.
∴ ∠BCE=∠DCE.又 CE=CE,
∴ △BCE≌△COB(SAS).
∴ ∠CBE=∠CDE.
∵ 在菱形ABCD中,AB∥CD, ∴∠AFD=∠FDC
∴ ∠AFD=∠CBE.
例2: 如图1,已知菱形ABCD的周长为16cm,∠ABC=120°,求对角线BD和AC及菱形的面积.
分析:菱形具有四边相等,对角线互相垂直平分并平分一组对角等性质.知道了周长可求到边长,根据∠ABC=120°可得到等边三角形,进而可求到对角线的长,根据菱形的面积等于对角线乘积的一半可求到面积.
解:在菱形ABCD中,AB+BC+CD+AD=16cm,
所以AB=AD=BC=CD=16×=4(cm),
由∠ABC=120°,对角线BD平分∠ABC,得∠ABD=60°,
又因为AD=AB,
所以△ABD是等边三角形,BD=AB=4cm,
因为菱形对角线互相垂直平分, 图1
所以OB=2cm,
在Rt△AOB中,
AO=
所以AC=2OA=2×2=4(cm).
所以S菱形ABCD=AC·BD=×2×4=4(cm2).
例3:如图,四边形ABCD是菱形,∠ACD=30°.求∠BDA、∠ABC的度数.
分析:根据菱形的对角线平分一组对角可知∠DCA=∠BCA=30°,所以∠ACB=60°,根据菱形的对角相等,对边平行可求到∠BAD和∠ABC的度数.
解:因为菱形的对角线平分一组对角,所以∠BCD=2∠ACD=2×30°=60°,
因为菱形的对角相等,所以∠DAB=∠DCB=60°.
因为CD//AB,所以∠DCB+∠ABC=180°,
所以∠ABC=180°-60°=120°.
点评:菱形有关的计算题,主要涉及计算周长,边长以及面积等,解决问题需要将菱形的性质与直角三角形或等边三角形相结合.
例4:例3 如图3,矩形ABCD的对角线AC、BD相交于点O,AE//BD,BE//AC,AE与BE相交于点E,试判断AD与EO是否平行?说说你的理由.
分析:要判断AD与EO是否平行,根据四边形ABCD是矩形,可知∠DAB=90°,如果OE⊥AB,则可说明AD//EO.而说明OE⊥AB,只要说明四边形AEBO是菱形即可.
解:AD//EO.
理由:因为AE//BD,BE//AC,所以四边形AEBO是平行四边形,
所以OA=BE,BO=EA,
因为O是矩形ABCD对角线的交点,所以OA=OB,
所以OA=AE=EB=BO, 图3
所以四边形AEBO是菱形.
所以OE⊥AB,
因为∠DAB=90°,所以DA⊥AB,
所以AD//EO.
例5: 如图3,四边形ABCD是菱形,CE⊥AB,交AB的延长线于点E,CF⊥AD,交AD的延长线于点F.请你猜猜CE与CF的大小有什么关系?并试说明你的猜想.
分析:本题是一道结论猜想探索题,主要考查菱形的性质的应用.观察图形结合已知条件,可得CD=BC,∠CEB=∠CFD=90°,又根据菱形的对边平行,可得到∠CBE=∠DAB=∠FDC,借助三角形全等,可猜想CE=CF.
解: ∵四边形ABCD是菱形,
∴ BC=DC,AD∥BC,CD∥AB.
∴∠DAB=∠CBE,∠DAB=∠FDC.
∴∠CBE=∠FDC.
又CE⊥AE,CF⊥AF,
∴∠CEB=∠CFD=90°.
∴ Rt△BEC≌Rt△DFC.
∴ CE=CF.
类型之二:菱形的判定
例1:如图,在△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.求证:四边形ACEF是菱形.
解析:若四边形ACEF是菱形,又∠BAC=60°,容易推得△ACE和△AEF都是等边三角形.反过来,要证明四边形ACEF是菱形,可从证明△ACE和△AEF都是等边三角形入手.
这样,容易证明四边形ACEF是有一组邻边相等的平行四边形.
证明:由∠ACB=90°,∠BAC=60°,得∠B=30°.
因为DE垂直平分BC,垂足为D,交AB于点E,
所以BE=CE,∠ECB=∠B=30°.
所以∠ACE=90°-∠ECB=60°.
因为∠BAC=60°,
所以△ACE是等边三角形,∠CEA=60°,CE=AE.
因为∠AEF=∠BED=90°-∠B=60°,AF=CE=AE,
所以△AEF是等边三角形,∠EAF=60°.
所以∠CEA =∠EAF,CE∥AF.
因为AF=CE,
所以四边形ACEF是平行四边形.
因为AC=CE,
四边形ACEF是菱形.
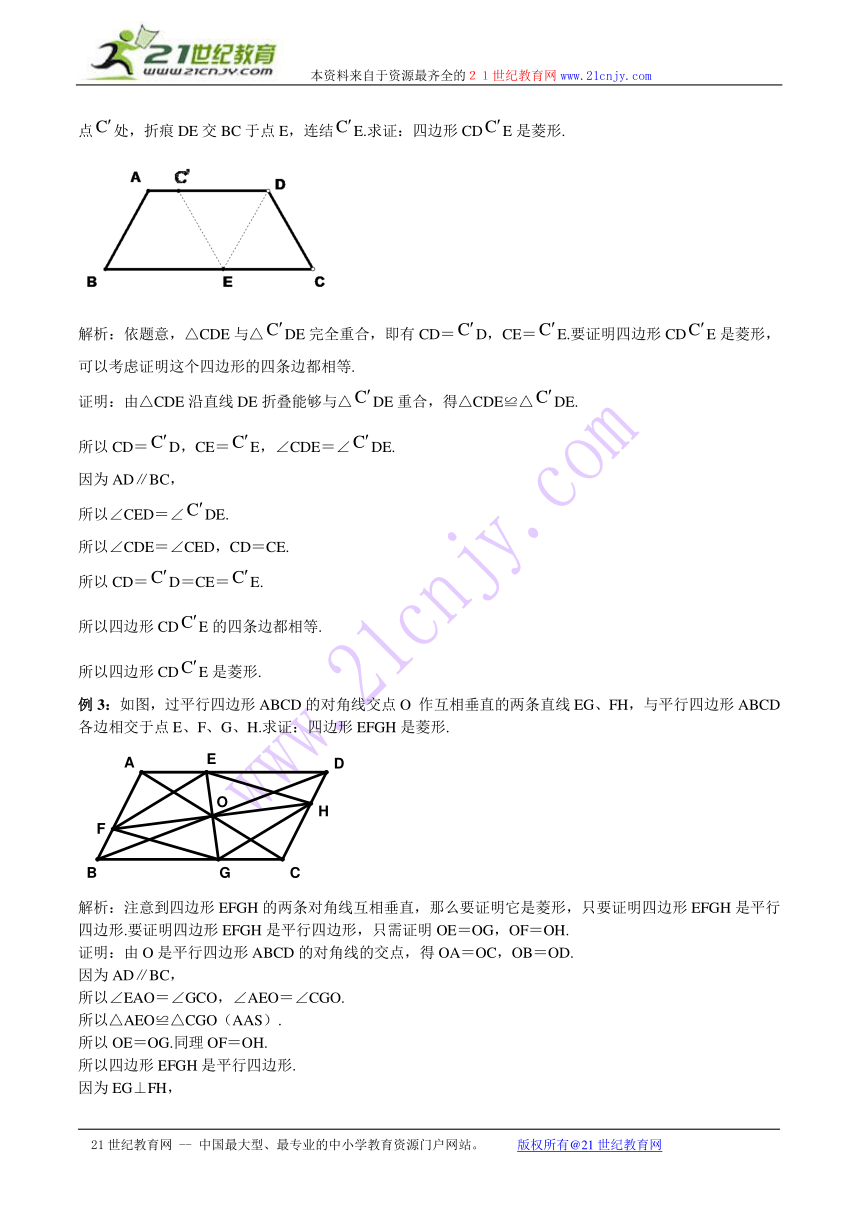
例2:如图,在梯形ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点处,折痕DE交BC于点E,连结E.求证:四边形CDE是菱形.
解析:依题意,△CDE与△DE完全重合,即有CD=D,CE=E.要证明四边形CDE是菱形,可以考虑证明这个四边形的四条边都相等.
证明:由△CDE沿直线DE折叠能够与△DE重合,得△CDE≌△DE.
所以CD=D,CE=E,∠CDE=∠DE.
因为AD∥BC,
所以∠CED=∠DE.
所以∠CDE=∠CED,CD=CE.
所以CD=D=CE=E.
所以四边形CDE的四条边都相等.
所以四边形CDE是菱形.
例3:如图,过平行四边形ABCD的对角线交点O 作互相垂直的两条直线EG、FH,与平行四边形ABCD各边相交于点E、F、G、H.求证:四边形EFGH是菱形.
解析:注意到四边形EFGH的两条对角线互相垂直,那么要证明它是菱形,只要证明四边形EFGH是平行四边形.要证明四边形EFGH是平行四边形,只需证明OE=OG,OF=OH.
证明:由O是平行四边形ABCD的对角线的交点,得OA=OC,OB=OD.
因为AD∥BC,
所以∠EAO=∠GCO,∠AEO=∠CGO.
所以△AEO≌△CGO(AAS).
所以OE=OG.同理OF=OH.
所以四边形EFGH是平行四边形.
因为EG⊥FH,
所以四边形EFGH是菱形.
类型之三:菱形与矩形的综合
1.开放型问题
例1:如图,在△中,为边的中点,过点分别作∥交于点,
∥交于点.
(1)证明:△≌△ ;
(2)如果给△添加一个条件,使四边形成为菱形,则该条是 ;
如果给△添加一个条件,使四边形成为矩形,则该条件是 .
(均不再增添辅助线) 请选择一个结论进行证明.
【解】(1)证明: ∵
∴ )
∵ ∴
又∵∴≌
(2)或或;°或°或°
① 证明:∵ ∴四边形为平行四边形
又∵ ∴ ∴ ∴
由≌可得:
∴∴四边形为菱形
② 证明:同理可证四边形为平行四边形
∵∴四边形为矩形
【评注】本题一道探索条件、补充条件的开放型几何试题,它考查了矩形及菱形的判定及三角形全等的判定知识,解决这类问题的方法是假设结论成立,逐步探索其成立的条件
2.操作性问题
例2:将两张宽度相等的矩形纸片叠放在一起得到如图1所示的四边形ABCD.
(1)求证:四边形是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么菱形的周长是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.
【解】(1)如图答2,因为.
所以四边形为平行四边形.
分别过点作,,垂足分别为点,
则.
因为,所以.
所以,所以四边形为菱形.
(2)存在最小值和最大值.(判断不准确,不得分)
①当时,菱形为正方形,周长最小值为8.
②当为矩形纸片的对角线时,设,如图答3,在中,
,.所以周长最大值为17.
【评注】这是一道探索结论试题.解决这类问题的方法是根据条件,结合已学的知识、数学思想方法,通过分析、归纳逐步得出结论,或通过观察、实验、猜想、论证的方法求解.
3.方案设计型
例3:如图甲,李叔叔想要检测雕塑底座正面四边形是否为矩形,但他随身只带了有刻度的卷尺,请你设计一种方案,帮助李叔叔检测四边形是否为矩形(图乙供设计备用).
解:方案如下:
①用卷尺分别比较与与的长度,当,且时,四边形为平行四边形;否则四边形不是平行四边形,从而不是矩形.
②当四边形是平行四边形时,用卷尺比较对角线与的长度.当时,四边形是矩形;否则四边形不是矩形.
也可设计以下方案.
方案一:先用勾股定理逆定理测量一个角是否为直角,然后用同样的方法再测量另外两个角是否也为直角,并给出判断;
方案二:先测量四边形是否为平行四边形,再用勾股定理逆定理测量其中一个角是否为直角,并给出判断.
【评注】这是一道几何型的方案设计题,解答此类题应善于联想相关图形性质,进行充分发散思维,经筛选比较,可找出较合适方案来.
4.综合探究型
例4:如图7,矩形纸片的边长分别为.将纸片任意翻折(如图8),折痕为.(在上),使顶点落在四边形内一点,的延长线交直线于,再将纸片的另一部分翻折,使落在直线上一点,且所在直线与所在直线重合(如图9)折痕为.
(1)猜想两折痕之间的位置关系,并加以证明.
(2)若的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕间的距离有何变化?请说明理由.
(3)若的角度在每次翻折的过程中都为(如图10),每次翻折后,非重叠部分的四边形,及四边形的周长与有何关系,为什么?
【解】(1)
因为四边形是矩形,所以,且在直线上,则有
所以,由翻折可得:,
,所以,故.
(2)两折痕间的距离不变
过作,则,
因为的角度不变,所以的角度也不变,则所有的都是平行的
又因为,所以所有的都是相等的
又因为,故的长不变.
(3)当时,四边形是正方形,
四边形是矩形.
因为,,
所以矩形的周长为.
同理可得矩形的周长为,所以两个四边形的周长都为,与无关.
一、填空:
1.菱形具有而矩形不具有的性质有 .
2.菱形的两条对角线之比是3∶4,周长为60cm,则菱形的面积是 ,高是 .
3.如图菱形ABCD的一条对角线BD上一点O,到菱形一边AB的距离为2,那么点O到另外一边BC的距离 .
4.矩形的邻边之比为3∶4,对角线长10cm,则矩形的面积为 ;若矩形ABCD的对角线AC、BD相交点O,∠AOB=2∠BOC,对角线AC=20cm,则AD= ;如果矩形一条边上的中点与对边两个端点的连线互相垂直,且矩形的周长为24cm,那么矩形的面积为 ;如果矩形的两条对角线所成的钝角是120°,那么对角线与矩形短边的长度之比为 .
5、如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们的交角为300,则它们重叠部分的面积为 .
6、如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为 .
二、选择:
1、不能判定一个四边形是菱形的条件是( )
A、对角线互相平分且有一组邻边相等
B、四边相等
C、两组对角相等,且一条对角线平分一组对角
D、对角线互相垂直
2、一张矩形纸片纸对折(如图),然后沿图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A、三角形 B、矩形 C、菱形 D、梯形
3.菱形的对角线的平方和等于一边的( )
A.2倍 B.3倍 C.4倍 D.8倍
4.四个内角都相等的四边形一定是( )
A.任意四边形 B.矩形 C.菱形 D.正方形
5.下列命题中,正确的命题有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相平分且相等的四边形是矩形
④一条对角线平分一个内角的平行四边形是菱形
A.1个 B.2个 C.3个 D.4个
三、解答题:
1、已知:如图,BD是△ABC的角平分线,EF是BD的垂直平分线,
且交AB于E,交BC于点F,说明:四边形BFDE是菱形.
2、如图,平行四边形ABCD中,EF过AC的中点O,与边AD、BC分别相交于点E、F.
(1)试说明四边形AECF是平行四边形.
(2)若EF过AC的中点,且与AC垂直时,试说明四边形AECF是菱形.
(3)当EF与AC有怎样的数量和位置关系时,四边形AECF是矩形.
参考答案:
一、填空
1.对角线互相垂直,每一条对角线平分一组对角
2.216 cm2,14.4 cm
3.2
4.48cm2 ;10cm; 32cm2; 2:1;
5.2
6.2.4
二、选择
1.D 2.C 3.C 4.B 5.A
三、1、因为BD平分∠ABC所以∠ABD=∠CBD因为EF是BD的垂直平分线所以BE=DE因为∠EBD=∠EDB ∠EDB=∠DAF易说明△EOD≌△FOB(AAS)从而BE=DE=DF=BF
2、(1)因为平行四边形ABCD所以AD//BC所以∠OAC=∠ACF易说明△AOE≌△COF(AAS)所以AE=CF因为AE//CF所以四边形AECF是平行四边形.
(2)由(1)知四边形AECF是平行四边形因为AC⊥EF所以四边形是菱形(对角线互相垂直的平行四边形是菱形)
(3)EF=AC时四边形AECF是矩形.
一.填空
1.我们把__________叫做菱形.
2.菱形是特殊的_________,所以它不但具有一般_________的性质,而且还具有特殊的性质:(1)__________;(2)__________.
3.菱形既是_________图形,又是_________图形,它的______都是它的对称轴.
4.若菱形的周长为16cm,则此菱形的边长是______cm.
5.在菱形ABCD中,若∠ABD=72°,则∠ADC=_______,∠BAD=_______.
6.在菱形ABCD中,若对角线AC=6,BD=8,则CD=_______,此菱形的面积是______.
二.选择
7.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对角线互相平分 C.对边平行且相等 D.对角线互相垂直
8.如图1所示,在菱形ABCD中,对角线AC,BD相交于点O,若∠ABC=60°,则AC:BD等于( )
A.:1 B.1:2 C.:3 D.1:2
(1) (2)
9.若菱形ABCD的周长为8,对角线AC=2,则∠ABC的度数是( )
A.120° B.60° C.30° D.150°
10.依次连结菱形四条边的中点所构成的四边形是( )
A.菱形 B.矩形 C.一般平行四边形 D.一般四边形
11.在菱形ABCD中,若∠ADC=120°,对角线AC=6,则菱形的周长是( )
A.4 B.24 C.8 D.24
12.如图2所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是( )
A. D.8
三解答
13.如图所示,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足,AE=ED,求∠EBF的度数.
14.如图所示,在菱形OABC中,∠ABO=30°,OB=2,O是坐标原点,点A在x轴的负半轴上,求菱形OABC各顶点的坐标.
15.如图所示,在菱形ABCD中,已知E是BC上一点,且AE=AB,∠EAD=2∠BAE,
求证:BE=AF.
16.如图所示,在菱形ABCD中,∠A=108°,请将此菱形分割成四个等腰三角形.说明:(1)工具不限;(2)标出所画三角形的内角的度数;(3)用尽可能多的方法分割此菱形;(4)若有一条分割线不同,就是不同的分割方法.
答案:
1.一组邻边相等的平行四边形
2.平行四边形,平行四边形
(1)菱形的四条边相等
(2)菱形的对角线互相垂直,并且每条对角线平分线一组对角
3.中心对称,轴对称,每一条对角线所在的直线
4.4 5.144°,36° 6.5,24
7.D 8.C 9.B 10.B 11.C 12.A
13.60°
14.O(0,0),A(-2,0),B(-3,),(-1,)
15.提示:设∠BAE=x,列方程5x=180°,得x=36° 16.略
1.如图所示,四边形ABCD是平行四边形,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.
(1)求证:四边形DMNC是平行四边形;
(2)若要使四边形DMNC为菱形,则还需增加什么条件?请写出此条件,并证明之.
2.如图所示,在中,分别是,的平分线,和交于,试说明四边形的形状.
3. 如图所示,在平行四边形中,,以顶点为圆心,为半径画弧,交于点,交于点.观察图形后,请你写出两个你所学过的特殊三角形或四边形.
4. 如图所示,两条同等宽的高速公路在某处交叉,已知,公路宽为60米,求交叉区域的面积.
答案:1. (1)略 (2)AD=2AB等,略
2.
又是角平分线.
且平分.
,且是角平分线,
平分.
与垂直且互相平分.
四边形是菱形.
3.解:且,是等边三角形.
又且,
四边形是平行四边形.
又,
四边形是菱形.
4. 解:如图,由于,
四边形是平行四边形.由于,
又
.
四边形是菱形.
,且,
.
,设,则,
则.
.
.
课时作业:
A等级
1.选择题
(1)已知菱形两个邻角的比是1∶5,高是8 cm,则菱形的周长是( )
A.16 cm B.32 cm
C.64 cm D.128 cm
(2)已知菱形的周长为40 cm,两对角线长的比是3∶4,则两对角线的长分别是( )
A.6 cm,8 cm B.3 cm,4 cm
C.12 cm,16 cm D.24 cm,32 cm
(3)ABCD的对角线AC、BD相交于点O,下列条件中,不能判定ABCD是菱形的是( )
A. AB=AD B. AC⊥BD
C.∠A=∠D D.CA平分∠BCD
(4)下列命题中,真命题是( )
A.对角线相等且互相垂直的四边形是菱形
B.有一条对角线平分一组对角的四边形是平行四边形
C.对角线互相垂直的矩形是菱形
D.菱形的对角线相等
(5)如图4-37,矩形ABCD中,M是矩形外一点,且MA=MD,MB、MC交AD于E、F,则图中共有全等三角形( )
图4—37
A.3对 B.4对
C.5对 D.6对
(6)如图4-38,在菱形ABCD中,AE⊥BC,AF⊥CD,且E、F分别为BC、CD的中点,那么∠EAF等于( )
图4—38
A.75° B.60°
C.45° D.30°
(7)如图4-39,△BDC′是将矩形纸片ABCD沿对角线BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形( )
图4—39
A.2对 B.3对
C.4对 D.5对
(8)同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,如图4-40是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心( )
图4—40
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
2.填空题
(1)如图4-41,矩形ABCD的对角线AC和BD相交于点O,①图中有_____个等腰三角形,有_____个直角三角形;②若∠CAB=30°,则两条对角线相交所成的四个角分别为______.
图4—41
(2)直角三角形中,两条直角边长分别是12和5,则斜边中线长是_____.
(3)两条平行线被第三条直线所截,两组内错角的平分线相交所成的四边形是_____.
(4)矩形的两条对角线所夹的锐角为60°,一条对角线与短边的和为15,则对角线长是_____,短边的长是_____.
(5)菱形的面积为24 cm2,一条对角线的长为6 cm,则另一条对角线长为_____cm,边长为_____cm,高为_____cm.
(6)如图4-42,菱形ABCD中,DE⊥AB于E,∠ABC=3∠A,且DE=5 cm,则AB=_____.
图4—42
(7)现有一张长为40 cm,宽为20 cm的长方形纸片,如图4-43,要从中剪下长为18 cm,宽为12 cm的长方形纸片,则最多能剪出_____张.
图4—43
(8)在矩形ABCD中,E为AD边上一点,且BE平分∠ABC,BE=BC,则∠CED=_____度.
3.如图4-44,四边形ABCD是矩形,四边形AECF是菱形,若AB=2 cm,BC=4 cm,求四边形AECF的面积.
图4—44
4.如图4-45,已知O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.求证:
OE⊥DC.
图4—45
5.以下是一道题目及其解答过程:
已知:如图4-47,从菱形ABCD对角线的交点O分别向各边引垂线,垂足分别是E、F、G、H.
求证:四边形EFGH是矩形.
图4—47
证明:∵四边形ABCD是菱形,
∴AO=CO,∠AOD=∠COD=90°. ①
又∵DO=DO,∴△AOD≌△COD. ②
∵OH、OG分别是Rt△AOD和Rt△COD斜边上的高,
∴OH=OG. ③
同理OH=OE,OE=OF,则OH=OE=OF=OG.
∴EG与HF相等且互相平分.
∴四边形EFGH是矩形. ④
以上证明过程中( )
A.①到②有错误 B.②到③有错误
C.③到④有错误 D.没有错误
B等级
1.判定一个四边形是菱形的方法有:
(1)菱形的定义:有一组邻边______的_______是菱形;
(2)四条边__________的四边形是菱形;
(3)对角线____的_________的是菱形.
2.在四边形ABCD中,AC⊥BD,AB∥CD,请你添上一个条件:_________,使得四边形ABCD是菱形.
3.如图1所示,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,连结DE,DF,EF,若使四边形ADFE是菱形,则需添加的条件是__________.
(1) (2) (3) (4)
4.如图2所示,点D,E,F分别是等边△ABC的边AB,AC,BC的中点,连结DE,DF,EF,则图中有______个菱形.
5.依次连结矩形四条边的中点所构成的四边形是________.
6.如图3所示,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是________.
7.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
8.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相等且相互垂直
9.若依次连结四边形各条边的中点所构成的四边形是菱形,则原四边形一定是( )
A.矩形 B.菱形 C.平行四边形 D.对角线相等的四边形
10.右图4是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,在墙上悬挂晾衣架的两个铁钉A,B之间的距离为20cm,则∠A的度数是( )
A.120° B.135° C.108° D.150°
11.在直角坐标系中,点A(-1,0),B(1,0),C(0,),若使以点A,B,C,D为顶点的四边形是菱形,则符合条件的点D的个数是( )
A.1个 B.2个 C.3个 D.4个
12.如图所示,平行四边形ABCD的对角线相交于点O,AB=,CO=2,BD=2.
(1)直线AC与BD垂直吗?为什么?(2)四边形ABCD是菱形吗?请说明理由.
13.如图所示,矩形ABCD的对角线相交于点O,分别过点A,D作AE∥BD,DE∥AC交于点E,求证:四边形AODE是菱形.
14.如图所示,平行四边形ABCD的对角线AC的垂直平分线与AD,BC,AC分别交于E,F,O,求证:四边形AFCE是菱形.
C等级
1. 菱形的相邻两角之比为1:2,那么它所对的对角线与边长之比为( )
A. B.
C. D.
2. 在菱形中,的平分线与之间的关系是( )
A.相等 B.互相垂直但不平分
C.垂直平分 D.互相平分但不垂直
3. 在菱形中,,且分别是的中点,那么( )
A. B. C. D.
4. 菱形的两条对角线长是8和6,则菱形的周长是 ,面积是 .
5. 菱形中,为垂足,,则 .
6. 若四边形为平行四边形,请补充条件 (一个即可)使四边形为菱形.
7. 已知菱形的两对角线长为6cm和8cm,则菱形的周长为 ,面积是 .
8. 已知菱形的面积为,对角线,则菱形边长为 .
9. 已知:如图所示,中,分别是上的点,且,.要使是一个菱形,在不改变图形的前提下,你需添加的一个条件是 .
10. 菱形是轴对称图形,它的对称轴有( )
A.1条 B.2条 C.3条 D.4条
11. 在菱形中,对角线相交于点,则图形中有( )对全等的直角三角形.
A.3 B.4 C.5 D.6
12. 能判别四边形是菱形的条件是( )
A.四边形的对角线相等
B.四边形的两条对角线互相垂直
C.四边形的对角线相等且互相垂直
D.四边形的两条对角线互相垂直平分
13. 下列条件能判断四边形是菱形的条件是( )
A.对角线互相平分 B.对角线互相垂直
C.邻边相等 D.对角线互相垂直且平分
14. 已知菱形中,相交于点,如图所示,并且若,求菱形的面积.
15. 如图所示,是中的的平分线,交于.
(1)求证:四边形是菱形.
(2)如果,,求菱形的面积.
.
16. 已知是等腰三角形,如图所示,是底边上的中点,且交于,交于,试说明与的关系.
课时作业答案:
A等级答案:
1.(1)C (2)C (3)C (4)C (5)B (6)B (7)C (8)D
2.(1)①4 4 ②120° 60° 120° 60° (2)6.5 (3)矩形 (4)10 5
(5)8 5 (6)5 cm (7)3 (8)67.5
3.5 cm2.提示:设菱形的边长为x cm,则AE=x cm,BE=(4-x) cm,由AB2+BE2=AE2,得22+(4-x)2=x2.
4.提示:证四边形OCED是菱形.
5.C
B等级答案:
1.(1)邻边相等,平行四边形 (2)相等 (3)相等,平行四边形
2.AB=CD或AD∥BC 3.AB=AC 4.3 5.菱形 6.
7.C 8.D 9.D 10.A 11.C
12.(1)AC⊥BD,略 (2)菱形,略 13.略 14.略
C等级答案:
1:D2:C3:D4:20,245:6:7:20cm 8:cm
9:答:可以是是的角平分线,
其中的一个.
10:B11:D12:D13:D
14:解:设,
则,
.
即:..
.
15:解:(1),
四边形是平行四边形.
四边形是菱形.
(2)由于,
则为等边三角形,
,连结与相交于,则,
.
.
16:解:与互相垂直平分,理由如下:
四边形是平行四边形.
四边形是菱形.
与互相垂直平分.
A
B
C
D
(图1)
A
B
C
D
(图答2)
F
E
A
B
C
D
(图答3)
C
G
(图甲)
(图乙)
A
M
D
Q
C
P
B
M
D
Q
C
P
A
B
N
M
D
Q
C
P
A
B
N
A
D
C
B
a
b
图7
图8
图9
图10
M
D
Q
C
P
A
B
N
H
30°
A
B
C
E
F
D
G
A
B
E
C
D
F
A
D
C
B
A
F
C
B
E
D
F
C
D
B
E
A
B
A
D
O
C
A
E
B
C
F
D
1
2
A
A
E
F
O
C
D
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第十九章 四边形
第11课时 菱形概念、性质、判定
通过本节的学习需要掌握菱形概念,知道菱形与平行四边形的关系.理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积.通过运用菱形知识解决具体问题,提高分析能力和观察能力.根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
点击一:定义:
定义:有一组邻边相等的平行四边形叫做菱形.
【强调】 菱形(1)是平行四边形;(2)一组邻边相等.
点击二:菱形的性质
(1)具有平行四边形的性质
(2)菱形的四条边相等
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
注意:(1)菱形是特殊的平行四边形,是中心对称图形,过中心的任意直线可将菱形分成完全全等的两部分(2)菱形也是轴对称图形,有两条对称轴,对称轴的交点就是对称中心
针对练习:
1.如图1,已知菱形ABCD的周长为16cm,∠ABC=120°,求对角线BD和AC的长.
解析:知道了菱形的周长可以求到菱形的边长,再根据菱形的性质可得到△ABD是等边三角形,这样可求得对角线BD的长,最后借助勾股定理求得AC的长.
解:在菱形ABCD中,AB+BC+CD+AD=16cm,∠ABC=120°.
∴AB=AD=BC=CD=4cm.
由对角线BD平分∠ABC,得∠ABD=60°.
∴△ABD是等边三角形,BD=AB=4cm.
∵菱形的对角线互相垂直平分,∴OB=2cm.
在Rt△AOB中,(cm).
∴(cm).
点击三:菱形的判定
(1)定义
(2)对角线互相垂直的平行四边形是菱形
(3)四条边相等的四边形是菱形
针对练习:
1.如图4,在△ABC中,AB=AC,AD是BC边上的高,过点D作DE∥AB交AC于点E,作DF∥AC交AB于点F,四边形AFDE是菱形吗?说说你的理由.
答案:先证四边形AFDE是平行四边形,再证邻边相等)
2. 如图2,的两条对角线AC、BD相交于点O,AB=10,AO=8,OB=6.
(1)AC、BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
解析:(1)要判断AC与BD是否垂直,可以根据已知条件,看△AOB是否是直角三角形,为此需要利用勾股定理的逆定理来解决;
(2)此问的解决是建立在(1)的基础上的,解决了(1),此问也就解决了.
解:在△ABO中,
∵AB=10,OA=8,OB=6,62+82=102,
∴OA2+OB2=AB2.
∴△ABO是直角三角形.
且∠AOB为直角.
∴ AC⊥BD.
(2)∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形.
点击四:菱形的面积公式
菱形的面积公式是 (其中a、b是菱形的两条对角线分别的长).即:“菱形的面积等于它的两条对角线长的积的一半”.当不易求出对角线长时,就用平行四边形面积的一般计算方法计算菱形面积S=底×高.
类型之一:菱形的性质
例1: 已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
证明:∵ 四边形ABCD是菱形,
∴ CB=CD, CA平分∠BCD.
∴ ∠BCE=∠DCE.又 CE=CE,
∴ △BCE≌△COB(SAS).
∴ ∠CBE=∠CDE.
∵ 在菱形ABCD中,AB∥CD, ∴∠AFD=∠FDC
∴ ∠AFD=∠CBE.
例2: 如图1,已知菱形ABCD的周长为16cm,∠ABC=120°,求对角线BD和AC及菱形的面积.
分析:菱形具有四边相等,对角线互相垂直平分并平分一组对角等性质.知道了周长可求到边长,根据∠ABC=120°可得到等边三角形,进而可求到对角线的长,根据菱形的面积等于对角线乘积的一半可求到面积.
解:在菱形ABCD中,AB+BC+CD+AD=16cm,
所以AB=AD=BC=CD=16×=4(cm),
由∠ABC=120°,对角线BD平分∠ABC,得∠ABD=60°,
又因为AD=AB,
所以△ABD是等边三角形,BD=AB=4cm,
因为菱形对角线互相垂直平分, 图1
所以OB=2cm,
在Rt△AOB中,
AO=
所以AC=2OA=2×2=4(cm).
所以S菱形ABCD=AC·BD=×2×4=4(cm2).
例3:如图,四边形ABCD是菱形,∠ACD=30°.求∠BDA、∠ABC的度数.
分析:根据菱形的对角线平分一组对角可知∠DCA=∠BCA=30°,所以∠ACB=60°,根据菱形的对角相等,对边平行可求到∠BAD和∠ABC的度数.
解:因为菱形的对角线平分一组对角,所以∠BCD=2∠ACD=2×30°=60°,
因为菱形的对角相等,所以∠DAB=∠DCB=60°.
因为CD//AB,所以∠DCB+∠ABC=180°,
所以∠ABC=180°-60°=120°.
点评:菱形有关的计算题,主要涉及计算周长,边长以及面积等,解决问题需要将菱形的性质与直角三角形或等边三角形相结合.
例4:例3 如图3,矩形ABCD的对角线AC、BD相交于点O,AE//BD,BE//AC,AE与BE相交于点E,试判断AD与EO是否平行?说说你的理由.
分析:要判断AD与EO是否平行,根据四边形ABCD是矩形,可知∠DAB=90°,如果OE⊥AB,则可说明AD//EO.而说明OE⊥AB,只要说明四边形AEBO是菱形即可.
解:AD//EO.
理由:因为AE//BD,BE//AC,所以四边形AEBO是平行四边形,
所以OA=BE,BO=EA,
因为O是矩形ABCD对角线的交点,所以OA=OB,
所以OA=AE=EB=BO, 图3
所以四边形AEBO是菱形.
所以OE⊥AB,
因为∠DAB=90°,所以DA⊥AB,
所以AD//EO.
例5: 如图3,四边形ABCD是菱形,CE⊥AB,交AB的延长线于点E,CF⊥AD,交AD的延长线于点F.请你猜猜CE与CF的大小有什么关系?并试说明你的猜想.
分析:本题是一道结论猜想探索题,主要考查菱形的性质的应用.观察图形结合已知条件,可得CD=BC,∠CEB=∠CFD=90°,又根据菱形的对边平行,可得到∠CBE=∠DAB=∠FDC,借助三角形全等,可猜想CE=CF.
解: ∵四边形ABCD是菱形,
∴ BC=DC,AD∥BC,CD∥AB.
∴∠DAB=∠CBE,∠DAB=∠FDC.
∴∠CBE=∠FDC.
又CE⊥AE,CF⊥AF,
∴∠CEB=∠CFD=90°.
∴ Rt△BEC≌Rt△DFC.
∴ CE=CF.
类型之二:菱形的判定
例1:如图,在△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.求证:四边形ACEF是菱形.
解析:若四边形ACEF是菱形,又∠BAC=60°,容易推得△ACE和△AEF都是等边三角形.反过来,要证明四边形ACEF是菱形,可从证明△ACE和△AEF都是等边三角形入手.
这样,容易证明四边形ACEF是有一组邻边相等的平行四边形.
证明:由∠ACB=90°,∠BAC=60°,得∠B=30°.
因为DE垂直平分BC,垂足为D,交AB于点E,
所以BE=CE,∠ECB=∠B=30°.
所以∠ACE=90°-∠ECB=60°.
因为∠BAC=60°,
所以△ACE是等边三角形,∠CEA=60°,CE=AE.
因为∠AEF=∠BED=90°-∠B=60°,AF=CE=AE,
所以△AEF是等边三角形,∠EAF=60°.
所以∠CEA =∠EAF,CE∥AF.
因为AF=CE,
所以四边形ACEF是平行四边形.
因为AC=CE,
四边形ACEF是菱形.
例2:如图,在梯形ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点处,折痕DE交BC于点E,连结E.求证:四边形CDE是菱形.
解析:依题意,△CDE与△DE完全重合,即有CD=D,CE=E.要证明四边形CDE是菱形,可以考虑证明这个四边形的四条边都相等.
证明:由△CDE沿直线DE折叠能够与△DE重合,得△CDE≌△DE.
所以CD=D,CE=E,∠CDE=∠DE.
因为AD∥BC,
所以∠CED=∠DE.
所以∠CDE=∠CED,CD=CE.
所以CD=D=CE=E.
所以四边形CDE的四条边都相等.
所以四边形CDE是菱形.
例3:如图,过平行四边形ABCD的对角线交点O 作互相垂直的两条直线EG、FH,与平行四边形ABCD各边相交于点E、F、G、H.求证:四边形EFGH是菱形.
解析:注意到四边形EFGH的两条对角线互相垂直,那么要证明它是菱形,只要证明四边形EFGH是平行四边形.要证明四边形EFGH是平行四边形,只需证明OE=OG,OF=OH.
证明:由O是平行四边形ABCD的对角线的交点,得OA=OC,OB=OD.
因为AD∥BC,
所以∠EAO=∠GCO,∠AEO=∠CGO.
所以△AEO≌△CGO(AAS).
所以OE=OG.同理OF=OH.
所以四边形EFGH是平行四边形.
因为EG⊥FH,
所以四边形EFGH是菱形.
类型之三:菱形与矩形的综合
1.开放型问题
例1:如图,在△中,为边的中点,过点分别作∥交于点,
∥交于点.
(1)证明:△≌△ ;
(2)如果给△添加一个条件,使四边形成为菱形,则该条是 ;
如果给△添加一个条件,使四边形成为矩形,则该条件是 .
(均不再增添辅助线) 请选择一个结论进行证明.
【解】(1)证明: ∵
∴ )
∵ ∴
又∵∴≌
(2)或或;°或°或°
① 证明:∵ ∴四边形为平行四边形
又∵ ∴ ∴ ∴
由≌可得:
∴∴四边形为菱形
② 证明:同理可证四边形为平行四边形
∵∴四边形为矩形
【评注】本题一道探索条件、补充条件的开放型几何试题,它考查了矩形及菱形的判定及三角形全等的判定知识,解决这类问题的方法是假设结论成立,逐步探索其成立的条件
2.操作性问题
例2:将两张宽度相等的矩形纸片叠放在一起得到如图1所示的四边形ABCD.
(1)求证:四边形是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么菱形的周长是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.
【解】(1)如图答2,因为.
所以四边形为平行四边形.
分别过点作,,垂足分别为点,
则.
因为,所以.
所以,所以四边形为菱形.
(2)存在最小值和最大值.(判断不准确,不得分)
①当时,菱形为正方形,周长最小值为8.
②当为矩形纸片的对角线时,设,如图答3,在中,
,.所以周长最大值为17.
【评注】这是一道探索结论试题.解决这类问题的方法是根据条件,结合已学的知识、数学思想方法,通过分析、归纳逐步得出结论,或通过观察、实验、猜想、论证的方法求解.
3.方案设计型
例3:如图甲,李叔叔想要检测雕塑底座正面四边形是否为矩形,但他随身只带了有刻度的卷尺,请你设计一种方案,帮助李叔叔检测四边形是否为矩形(图乙供设计备用).
解:方案如下:
①用卷尺分别比较与与的长度,当,且时,四边形为平行四边形;否则四边形不是平行四边形,从而不是矩形.
②当四边形是平行四边形时,用卷尺比较对角线与的长度.当时,四边形是矩形;否则四边形不是矩形.
也可设计以下方案.
方案一:先用勾股定理逆定理测量一个角是否为直角,然后用同样的方法再测量另外两个角是否也为直角,并给出判断;
方案二:先测量四边形是否为平行四边形,再用勾股定理逆定理测量其中一个角是否为直角,并给出判断.
【评注】这是一道几何型的方案设计题,解答此类题应善于联想相关图形性质,进行充分发散思维,经筛选比较,可找出较合适方案来.
4.综合探究型
例4:如图7,矩形纸片的边长分别为.将纸片任意翻折(如图8),折痕为.(在上),使顶点落在四边形内一点,的延长线交直线于,再将纸片的另一部分翻折,使落在直线上一点,且所在直线与所在直线重合(如图9)折痕为.
(1)猜想两折痕之间的位置关系,并加以证明.
(2)若的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕间的距离有何变化?请说明理由.
(3)若的角度在每次翻折的过程中都为(如图10),每次翻折后,非重叠部分的四边形,及四边形的周长与有何关系,为什么?
【解】(1)
因为四边形是矩形,所以,且在直线上,则有
所以,由翻折可得:,
,所以,故.
(2)两折痕间的距离不变
过作,则,
因为的角度不变,所以的角度也不变,则所有的都是平行的
又因为,所以所有的都是相等的
又因为,故的长不变.
(3)当时,四边形是正方形,
四边形是矩形.
因为,,
所以矩形的周长为.
同理可得矩形的周长为,所以两个四边形的周长都为,与无关.
一、填空:
1.菱形具有而矩形不具有的性质有 .
2.菱形的两条对角线之比是3∶4,周长为60cm,则菱形的面积是 ,高是 .
3.如图菱形ABCD的一条对角线BD上一点O,到菱形一边AB的距离为2,那么点O到另外一边BC的距离 .
4.矩形的邻边之比为3∶4,对角线长10cm,则矩形的面积为 ;若矩形ABCD的对角线AC、BD相交点O,∠AOB=2∠BOC,对角线AC=20cm,则AD= ;如果矩形一条边上的中点与对边两个端点的连线互相垂直,且矩形的周长为24cm,那么矩形的面积为 ;如果矩形的两条对角线所成的钝角是120°,那么对角线与矩形短边的长度之比为 .
5、如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们的交角为300,则它们重叠部分的面积为 .
6、如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为 .
二、选择:
1、不能判定一个四边形是菱形的条件是( )
A、对角线互相平分且有一组邻边相等
B、四边相等
C、两组对角相等,且一条对角线平分一组对角
D、对角线互相垂直
2、一张矩形纸片纸对折(如图),然后沿图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A、三角形 B、矩形 C、菱形 D、梯形
3.菱形的对角线的平方和等于一边的( )
A.2倍 B.3倍 C.4倍 D.8倍
4.四个内角都相等的四边形一定是( )
A.任意四边形 B.矩形 C.菱形 D.正方形
5.下列命题中,正确的命题有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相平分且相等的四边形是矩形
④一条对角线平分一个内角的平行四边形是菱形
A.1个 B.2个 C.3个 D.4个
三、解答题:
1、已知:如图,BD是△ABC的角平分线,EF是BD的垂直平分线,
且交AB于E,交BC于点F,说明:四边形BFDE是菱形.
2、如图,平行四边形ABCD中,EF过AC的中点O,与边AD、BC分别相交于点E、F.
(1)试说明四边形AECF是平行四边形.
(2)若EF过AC的中点,且与AC垂直时,试说明四边形AECF是菱形.
(3)当EF与AC有怎样的数量和位置关系时,四边形AECF是矩形.
参考答案:
一、填空
1.对角线互相垂直,每一条对角线平分一组对角
2.216 cm2,14.4 cm
3.2
4.48cm2 ;10cm; 32cm2; 2:1;
5.2
6.2.4
二、选择
1.D 2.C 3.C 4.B 5.A
三、1、因为BD平分∠ABC所以∠ABD=∠CBD因为EF是BD的垂直平分线所以BE=DE因为∠EBD=∠EDB ∠EDB=∠DAF易说明△EOD≌△FOB(AAS)从而BE=DE=DF=BF
2、(1)因为平行四边形ABCD所以AD//BC所以∠OAC=∠ACF易说明△AOE≌△COF(AAS)所以AE=CF因为AE//CF所以四边形AECF是平行四边形.
(2)由(1)知四边形AECF是平行四边形因为AC⊥EF所以四边形是菱形(对角线互相垂直的平行四边形是菱形)
(3)EF=AC时四边形AECF是矩形.
一.填空
1.我们把__________叫做菱形.
2.菱形是特殊的_________,所以它不但具有一般_________的性质,而且还具有特殊的性质:(1)__________;(2)__________.
3.菱形既是_________图形,又是_________图形,它的______都是它的对称轴.
4.若菱形的周长为16cm,则此菱形的边长是______cm.
5.在菱形ABCD中,若∠ABD=72°,则∠ADC=_______,∠BAD=_______.
6.在菱形ABCD中,若对角线AC=6,BD=8,则CD=_______,此菱形的面积是______.
二.选择
7.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对角线互相平分 C.对边平行且相等 D.对角线互相垂直
8.如图1所示,在菱形ABCD中,对角线AC,BD相交于点O,若∠ABC=60°,则AC:BD等于( )
A.:1 B.1:2 C.:3 D.1:2
(1) (2)
9.若菱形ABCD的周长为8,对角线AC=2,则∠ABC的度数是( )
A.120° B.60° C.30° D.150°
10.依次连结菱形四条边的中点所构成的四边形是( )
A.菱形 B.矩形 C.一般平行四边形 D.一般四边形
11.在菱形ABCD中,若∠ADC=120°,对角线AC=6,则菱形的周长是( )
A.4 B.24 C.8 D.24
12.如图2所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是( )
A. D.8
三解答
13.如图所示,在菱形ABCD中,BE⊥AD,BF⊥CD,E,F为垂足,AE=ED,求∠EBF的度数.
14.如图所示,在菱形OABC中,∠ABO=30°,OB=2,O是坐标原点,点A在x轴的负半轴上,求菱形OABC各顶点的坐标.
15.如图所示,在菱形ABCD中,已知E是BC上一点,且AE=AB,∠EAD=2∠BAE,
求证:BE=AF.
16.如图所示,在菱形ABCD中,∠A=108°,请将此菱形分割成四个等腰三角形.说明:(1)工具不限;(2)标出所画三角形的内角的度数;(3)用尽可能多的方法分割此菱形;(4)若有一条分割线不同,就是不同的分割方法.
答案:
1.一组邻边相等的平行四边形
2.平行四边形,平行四边形
(1)菱形的四条边相等
(2)菱形的对角线互相垂直,并且每条对角线平分线一组对角
3.中心对称,轴对称,每一条对角线所在的直线
4.4 5.144°,36° 6.5,24
7.D 8.C 9.B 10.B 11.C 12.A
13.60°
14.O(0,0),A(-2,0),B(-3,),(-1,)
15.提示:设∠BAE=x,列方程5x=180°,得x=36° 16.略
1.如图所示,四边形ABCD是平行四边形,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.
(1)求证:四边形DMNC是平行四边形;
(2)若要使四边形DMNC为菱形,则还需增加什么条件?请写出此条件,并证明之.
2.如图所示,在中,分别是,的平分线,和交于,试说明四边形的形状.
3. 如图所示,在平行四边形中,,以顶点为圆心,为半径画弧,交于点,交于点.观察图形后,请你写出两个你所学过的特殊三角形或四边形.
4. 如图所示,两条同等宽的高速公路在某处交叉,已知,公路宽为60米,求交叉区域的面积.
答案:1. (1)略 (2)AD=2AB等,略
2.
又是角平分线.
且平分.
,且是角平分线,
平分.
与垂直且互相平分.
四边形是菱形.
3.解:且,是等边三角形.
又且,
四边形是平行四边形.
又,
四边形是菱形.
4. 解:如图,由于,
四边形是平行四边形.由于,
又
.
四边形是菱形.
,且,
.
,设,则,
则.
.
.
课时作业:
A等级
1.选择题
(1)已知菱形两个邻角的比是1∶5,高是8 cm,则菱形的周长是( )
A.16 cm B.32 cm
C.64 cm D.128 cm
(2)已知菱形的周长为40 cm,两对角线长的比是3∶4,则两对角线的长分别是( )
A.6 cm,8 cm B.3 cm,4 cm
C.12 cm,16 cm D.24 cm,32 cm
(3)ABCD的对角线AC、BD相交于点O,下列条件中,不能判定ABCD是菱形的是( )
A. AB=AD B. AC⊥BD
C.∠A=∠D D.CA平分∠BCD
(4)下列命题中,真命题是( )
A.对角线相等且互相垂直的四边形是菱形
B.有一条对角线平分一组对角的四边形是平行四边形
C.对角线互相垂直的矩形是菱形
D.菱形的对角线相等
(5)如图4-37,矩形ABCD中,M是矩形外一点,且MA=MD,MB、MC交AD于E、F,则图中共有全等三角形( )
图4—37
A.3对 B.4对
C.5对 D.6对
(6)如图4-38,在菱形ABCD中,AE⊥BC,AF⊥CD,且E、F分别为BC、CD的中点,那么∠EAF等于( )
图4—38
A.75° B.60°
C.45° D.30°
(7)如图4-39,△BDC′是将矩形纸片ABCD沿对角线BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形( )
图4—39
A.2对 B.3对
C.4对 D.5对
(8)同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,如图4-40是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心( )
图4—40
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
2.填空题
(1)如图4-41,矩形ABCD的对角线AC和BD相交于点O,①图中有_____个等腰三角形,有_____个直角三角形;②若∠CAB=30°,则两条对角线相交所成的四个角分别为______.
图4—41
(2)直角三角形中,两条直角边长分别是12和5,则斜边中线长是_____.
(3)两条平行线被第三条直线所截,两组内错角的平分线相交所成的四边形是_____.
(4)矩形的两条对角线所夹的锐角为60°,一条对角线与短边的和为15,则对角线长是_____,短边的长是_____.
(5)菱形的面积为24 cm2,一条对角线的长为6 cm,则另一条对角线长为_____cm,边长为_____cm,高为_____cm.
(6)如图4-42,菱形ABCD中,DE⊥AB于E,∠ABC=3∠A,且DE=5 cm,则AB=_____.
图4—42
(7)现有一张长为40 cm,宽为20 cm的长方形纸片,如图4-43,要从中剪下长为18 cm,宽为12 cm的长方形纸片,则最多能剪出_____张.
图4—43
(8)在矩形ABCD中,E为AD边上一点,且BE平分∠ABC,BE=BC,则∠CED=_____度.
3.如图4-44,四边形ABCD是矩形,四边形AECF是菱形,若AB=2 cm,BC=4 cm,求四边形AECF的面积.
图4—44
4.如图4-45,已知O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.求证:
OE⊥DC.
图4—45
5.以下是一道题目及其解答过程:
已知:如图4-47,从菱形ABCD对角线的交点O分别向各边引垂线,垂足分别是E、F、G、H.
求证:四边形EFGH是矩形.
图4—47
证明:∵四边形ABCD是菱形,
∴AO=CO,∠AOD=∠COD=90°. ①
又∵DO=DO,∴△AOD≌△COD. ②
∵OH、OG分别是Rt△AOD和Rt△COD斜边上的高,
∴OH=OG. ③
同理OH=OE,OE=OF,则OH=OE=OF=OG.
∴EG与HF相等且互相平分.
∴四边形EFGH是矩形. ④
以上证明过程中( )
A.①到②有错误 B.②到③有错误
C.③到④有错误 D.没有错误
B等级
1.判定一个四边形是菱形的方法有:
(1)菱形的定义:有一组邻边______的_______是菱形;
(2)四条边__________的四边形是菱形;
(3)对角线____的_________的是菱形.
2.在四边形ABCD中,AC⊥BD,AB∥CD,请你添上一个条件:_________,使得四边形ABCD是菱形.
3.如图1所示,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,连结DE,DF,EF,若使四边形ADFE是菱形,则需添加的条件是__________.
(1) (2) (3) (4)
4.如图2所示,点D,E,F分别是等边△ABC的边AB,AC,BC的中点,连结DE,DF,EF,则图中有______个菱形.
5.依次连结矩形四条边的中点所构成的四边形是________.
6.如图3所示,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是________.
7.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
8.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相等且相互垂直
9.若依次连结四边形各条边的中点所构成的四边形是菱形,则原四边形一定是( )
A.矩形 B.菱形 C.平行四边形 D.对角线相等的四边形
10.右图4是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,在墙上悬挂晾衣架的两个铁钉A,B之间的距离为20cm,则∠A的度数是( )
A.120° B.135° C.108° D.150°
11.在直角坐标系中,点A(-1,0),B(1,0),C(0,),若使以点A,B,C,D为顶点的四边形是菱形,则符合条件的点D的个数是( )
A.1个 B.2个 C.3个 D.4个
12.如图所示,平行四边形ABCD的对角线相交于点O,AB=,CO=2,BD=2.
(1)直线AC与BD垂直吗?为什么?(2)四边形ABCD是菱形吗?请说明理由.
13.如图所示,矩形ABCD的对角线相交于点O,分别过点A,D作AE∥BD,DE∥AC交于点E,求证:四边形AODE是菱形.
14.如图所示,平行四边形ABCD的对角线AC的垂直平分线与AD,BC,AC分别交于E,F,O,求证:四边形AFCE是菱形.
C等级
1. 菱形的相邻两角之比为1:2,那么它所对的对角线与边长之比为( )
A. B.
C. D.
2. 在菱形中,的平分线与之间的关系是( )
A.相等 B.互相垂直但不平分
C.垂直平分 D.互相平分但不垂直
3. 在菱形中,,且分别是的中点,那么( )
A. B. C. D.
4. 菱形的两条对角线长是8和6,则菱形的周长是 ,面积是 .
5. 菱形中,为垂足,,则 .
6. 若四边形为平行四边形,请补充条件 (一个即可)使四边形为菱形.
7. 已知菱形的两对角线长为6cm和8cm,则菱形的周长为 ,面积是 .
8. 已知菱形的面积为,对角线,则菱形边长为 .
9. 已知:如图所示,中,分别是上的点,且,.要使是一个菱形,在不改变图形的前提下,你需添加的一个条件是 .
10. 菱形是轴对称图形,它的对称轴有( )
A.1条 B.2条 C.3条 D.4条
11. 在菱形中,对角线相交于点,则图形中有( )对全等的直角三角形.
A.3 B.4 C.5 D.6
12. 能判别四边形是菱形的条件是( )
A.四边形的对角线相等
B.四边形的两条对角线互相垂直
C.四边形的对角线相等且互相垂直
D.四边形的两条对角线互相垂直平分
13. 下列条件能判断四边形是菱形的条件是( )
A.对角线互相平分 B.对角线互相垂直
C.邻边相等 D.对角线互相垂直且平分
14. 已知菱形中,相交于点,如图所示,并且若,求菱形的面积.
15. 如图所示,是中的的平分线,交于.
(1)求证:四边形是菱形.
(2)如果,,求菱形的面积.
.
16. 已知是等腰三角形,如图所示,是底边上的中点,且交于,交于,试说明与的关系.
课时作业答案:
A等级答案:
1.(1)C (2)C (3)C (4)C (5)B (6)B (7)C (8)D
2.(1)①4 4 ②120° 60° 120° 60° (2)6.5 (3)矩形 (4)10 5
(5)8 5 (6)5 cm (7)3 (8)67.5
3.5 cm2.提示:设菱形的边长为x cm,则AE=x cm,BE=(4-x) cm,由AB2+BE2=AE2,得22+(4-x)2=x2.
4.提示:证四边形OCED是菱形.
5.C
B等级答案:
1.(1)邻边相等,平行四边形 (2)相等 (3)相等,平行四边形
2.AB=CD或AD∥BC 3.AB=AC 4.3 5.菱形 6.
7.C 8.D 9.D 10.A 11.C
12.(1)AC⊥BD,略 (2)菱形,略 13.略 14.略
C等级答案:
1:D2:C3:D4:20,245:6:7:20cm 8:cm
9:答:可以是是的角平分线,
其中的一个.
10:B11:D12:D13:D
14:解:设,
则,
.
即:..
.
15:解:(1),
四边形是平行四边形.
四边形是菱形.
(2)由于,
则为等边三角形,
,连结与相交于,则,
.
.
16:解:与互相垂直平分,理由如下:
四边形是平行四边形.
四边形是菱形.
与互相垂直平分.
A
B
C
D
(图1)
A
B
C
D
(图答2)
F
E
A
B
C
D
(图答3)
C
G
(图甲)
(图乙)
A
M
D
Q
C
P
B
M
D
Q
C
P
A
B
N
M
D
Q
C
P
A
B
N
A
D
C
B
a
b
图7
图8
图9
图10
M
D
Q
C
P
A
B
N
H
30°
A
B
C
E
F
D
G
A
B
E
C
D
F
A
D
C
B
A
F
C
B
E
D
F
C
D
B
E
A
B
A
D
O
C
A
E
B
C
F
D
1
2
A
A
E
F
O
C
D
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
