5.1 相交线、垂线 、三线八角
文档属性
| 名称 | 5.1 相交线、垂线 、三线八角 |

|
|
| 格式 | rar | ||
| 文件大小 | 293.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-17 17:52:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第五章 相交线、平行线
第1课时 5.1 相交线、垂线 、三线八角
平面内两条直线的位置关系是“空间与图形”所要研究的基本问题,这些内容学生在前两个学段已经有所接触,本章在学生已有知识和经验的基础上,继续研究平面内两条直线的位置关系,首先研究了两条直线相交的情形,探究了两直线相交所成的角的位置和大小关系,给出了邻补角和对顶角概念,得出了“对顶角相等”的结论;垂直作为两条直线相交的特殊情形,与它有关的概念和结论是学习下一章“平面直角坐标系”的直接基础,本章对垂直的情形进行了专门的研究,探索得出了“过一点有且只有一条直线与已知直线垂直”“垂线段最短”等结论
点击一:知识点1:对顶角的概念
定义1:两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角.
定义2:一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角.如图1中,的∠1和∠2,∠3和∠4是对顶角. 无论是哪一种定义,都同样抓住了对顶角这个概念的本质特征:一是两个角有公共顶点;二是两个角的边互为反向延长线,因此说明只有两条直线相交才能产生对顶角.
说明:⑴判断两个角是否是对顶角,要看两个角是否是两条直线相交所得到的,还要看这两个角是不是有公共顶点.⑵对顶角是成对的.两条直线相交所构成的四个角中,共有两对对顶角.
点击二:邻补角的概念
定义1:两条直线相交构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角. 图2中,∠1和∠2有公共顶点O,且有一条公共边OA,另两边成一条直线,所以∠1和∠2是邻补角.
定义2:邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角.如图3中的∠1和∠2是邻补角.
对于邻补角的概念要抓住其本质特征:一是有公共顶点;二是有一条公共边;三是另一边互为反向延长线.
说明:⑴判断两个角是邻补角的关键是看这两个角的两边,其中一边是公共边,另外两边互为反向延长线.⑵邻补角是成对的,两条直线相交所构成的四个角中,有四对邻补角.
点击三:对顶角、邻补角的性质
对顶角相等,邻补角互补.
针对练习1:
1.如图所示,∠1和∠2是对顶角的图形有( )A毛
A.1个 B.2个 C.3个 D.4个
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )B
A.150° B.180° C.210° D.120°
(1) (2) (3)
3.下列说法正确的有( )B
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( ) A A.62° B.118° C.72° D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )D
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°
6.如图4所示,直线AB,CD,EF相交于点O,指出∠AOC, ∠EOB的对顶角, ∠AOC的邻补角.图中一共有几对对顶角 几对邻补角
解: ∠AOC的对顶角是∠BOD, ∠EOB的对顶角是∠AOF;∠AOC的邻补角是∠AOD, ∠BOC.图中共有6对对顶角,12对邻补角.
7.如图5,直线AB与CD相交于点O,OE平分∠AOD, ∠AOC=,求∠BOD, ∠AOE的度数.
解:∵AB与CD相交于点O (已知),
∴∠BOD=∠AOC=(对顶角相等).
∵∠AOC+∠AOD=(邻补角定义),
∴∠AOD=-=.
∵OE平分∠AOD (已知),
∴∠AO E=∠AOD =× = (角平分线定义).
点击四:垂线的定义
当两条直线相交的四个角中,有一个角是直角时,就说这两条直线是互相垂直的,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.抓住概念的三要素:两条直线;相交;一个角是直角.
说明:⑴线段与线段、线段与射线,射线与射线,线段或射线与直线垂直,特指它们所在的直线互相垂直.⑵两条直线互相垂直,则四个角为直角.反之也成立.
点击五:垂线的画法
让直角三角板的一条直角边与已知直线重合,沿直线左右移动三角板,使其另一条直角边经过已知点,沿此直角边画直线,则这条直线就是已知直线的垂线.用三角板画垂线的三个步骤:一贴;二过;三画.
注意:⑴经过直线上一点或直线外一点画已知直线的垂线,只能画出一条。
⑵如过一点画射线或线段的垂线,是指画它们所在直线的垂线,垂足有时在射线的反向延长线或线段的延长线上.
点击六:垂线的性质
第一个性质是:“过一点有且只有一条直线垂直于已知直线.”说的是垂线的存在性和唯一性,这是垂线作图的保证;垂线的第二个性质是:“垂线段最短”.它是定义“点到直线距离”这个概念的依据.
点击七:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
注意:垂线是直线;垂线段特指一条直线,是图形;点到直线的距离是指垂线段的长度,并且是一个数量,是有单位的.
针对练习2:
1.如图6所示, ∠BAC=,AD⊥BC,垂足为D,则下列结论:①AB与AC互相垂直; ②AD与AC互相垂直;③点C到AB的垂线段是线段AB; ④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.其中正确的有( )
A.2 B.3 C.4 D5
答:A.
2.如图7,直线AB,CD相交于点O,OE⊥CD, OF⊥AB, ∠DOF=,求∠BOE和∠AOC的度数.
解:∵,OE⊥CD, OF⊥AB (已知),
∴∠BOF=∠DOE=(垂直定义).
∵∠BOD=-=,
∴∠BOE=-=,
∴∠AOC=∠BOD=(对顶角相等).
3. 已知:如图1, ∠ACB=900,D是AB上一点,且∠ADC=∠BDC,写出图中互相垂直的线段,并说明理由.
解:图中互相垂直的线段有:AC⊥BC,CD⊥AB,CD⊥AD,CD⊥DB.
4. 如图2,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE, ∠1=15030′,则下列结论中不正确的是( ).
A.∠2=450 B.∠1=∠3
C. ∠AOD与∠1互为补角 D. ∠1的余角等于75030′
解:D
5.如图1所示,下列说法不正确的是( )C毛
A.点B到AC的垂线段是线段AB; B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段; D.线段BD是点B到AD的垂线段
6.下列说法正确的有( )C
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
点击八:三线八角
了解同位角、内错角、同旁内角的相关概念,在较复杂的图形中辨认同位角、内错角、同旁内角,是进一步学习平行线、四边形等后续知识的基础.
一般地:
(1)两条直线被第三条直线所截,构成八个角(简称“三线八角”),其中同位角4对,内错角2对,同旁内角2对.
(2)准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
(3)在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
(4)在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
形象感受三类角:
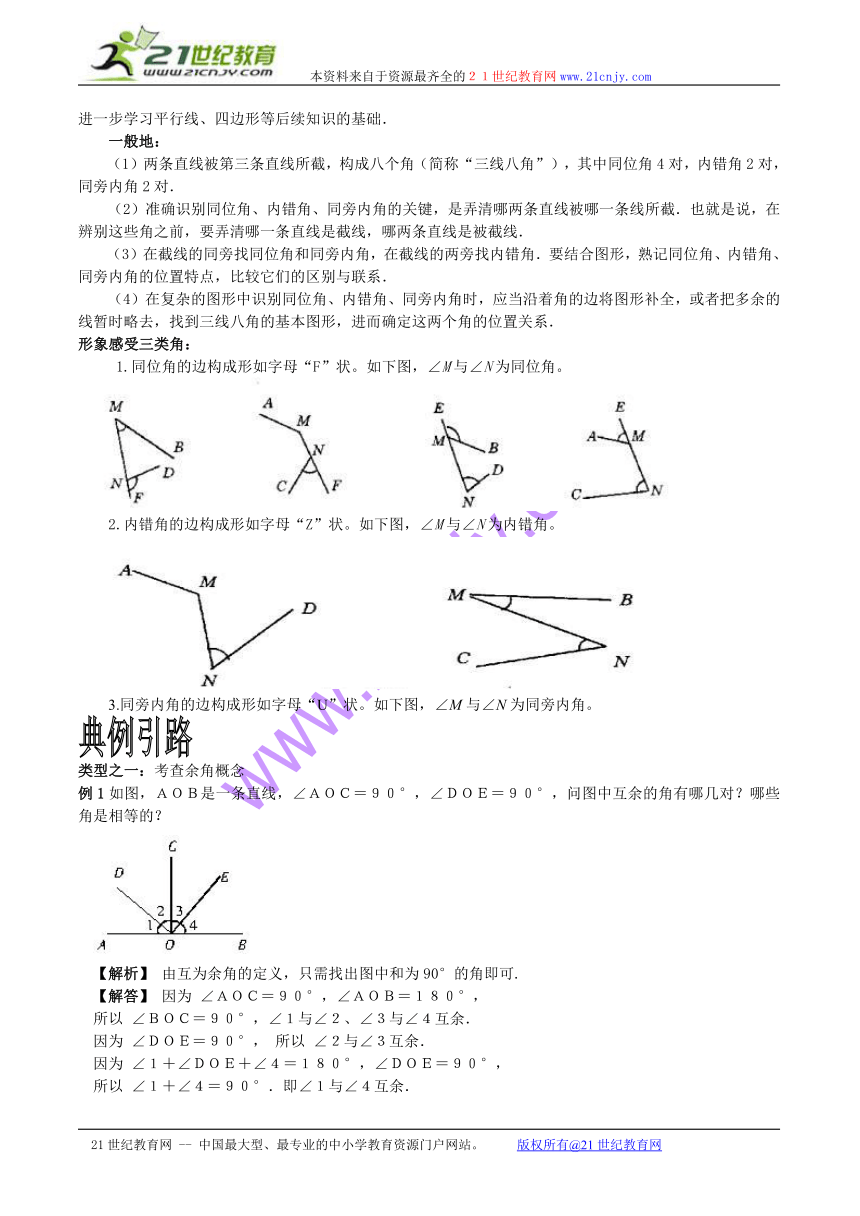
1.同位角的边构成形如字母“F”状。如下图,∠M与∠N为同位角。
2.内错角的边构成形如字母“Z”状。如下图,∠M与∠N为内错角。
3.同旁内角的边构成形如字母“U”状。如下图,∠M与∠N为同旁内角。
类型之一:考查余角概念
例1如图,AOB是一条直线,∠AOC=90°,∠DOE=90°,问图中互余的角有哪几对?哪些角是相等的?
【解析】 由互为余角的定义,只需找出图中和为90°的角即可.
【解答】 因为 ∠AOC=90°,∠AOB=180°,
所以 ∠BOC=90°,∠1与∠2、∠3与∠4互余.
因为 ∠DOE=90°, 所以 ∠2与∠3互余.
因为 ∠1+∠DOE+∠4=180°,∠DOE=90°,
所以 ∠1+∠4=90°.即∠1与∠4互余.
可以得到互余的角有:∠1与∠2,∠2与∠3,∠3与∠4,∠4与∠1.
因为 ∠1与∠2互余,∠2与∠3互余,
所以 ∠1=∠3(同角的余角相等).
因为∠3与∠4互余,∠3与∠2互余,
所以 ∠2=∠4(同角的余角相等).
可以得出相等的角有:∠1=∠3,∠2=∠4,∠AOC=∠DOE=∠BOC.
类型之二:考查对顶角和邻补角的定义及其性质的运用
例2:如图2所示,直线AB,CD,EF相交于点O,指出∠AOC, ∠EOB的对顶角, ∠AOC的邻补角.图中一共有几对对顶角 几对邻补角
【解析】找一个角的对顶角时,可分别反向延长这个角的两边,以延长线为边的角即是原角的对顶角.找一个角的邻补角时,可先固定一边,反向延长另一边,则由固定边和延长线组成的角即是原角的邻补角.∠AOC的邻补角应有两个,因为固定OA,反向延长OC;固定OC,反向延长OA.三条直线相交于一点,共有三组不同的两条直线相交,即AB与CD,AB与EF,CD与EF,每两组直线相交,就得到2对对顶角,4对邻补角,故有3×2对对顶角, 3×4对邻补角.
【解答】∠AOC的对顶角是∠BOD, ∠EOB的对顶角是∠AOF;∠AOC的邻补角是∠AOD, ∠BOC.图中共有6对对顶角,12对邻补角.
类型之三:考查垂线的定义和性质
例3:如图3所示, ∠BAC=,AD⊥BC,垂足为D,则下列结论:①AB与AC互相垂直; ②AD与AC互相垂直;③点C到AB的垂线段是线段AB; ④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.其中正确的有( )
A.2 B.3 C.4 D5
【解析】:根据垂直的特征:交角为直角,可得①正确, ②错误.C点到AB的垂线段应是AC,故③错误.点A到BC的距离是指线段AD的长度,故④错误. ⑤符合定义,正确,故⑥错误.
【解答】A.
类型之四:点到直线的距离
例4 如图3,OC是∠AOB的角平分线,点P是OC上一点.
(1)分别画出点P到∠AOB两边的垂线段;
(2)比较点P到∠AOB两边距离的大小;
(3)在OC上(除O,C外)任选点D,重复(1)、(2)步骤,并根据(2)的结果完成以下猜想:角平分线上的点到角两边的距离_______.
解析:根据垂线段的定义,画垂线段的实质是画垂线,
再取点P与垂足间的线段.
(1)如图4,PE,PF即为所求.
(2)点P到∠AOB两边的距离相等.
(3)相等.
类型之五:考查方程思想
例5:如图所示,由点O引出六条射线OA、OB、OC、OD、OE、OF,且AO⊥OB,OF平分∠BOC,OE平分∠AOD,若∠EOF=170°,求∠COD的度数.
【解析】:根据垂直、角平分线定义及角的和差关系可得∠EOF=∠FOC+∠COD+∠EOD,∠COF=∠BOC,∠EOD=∠AOD.
【解答】:设∠COD=.
因为OF平分∠BOC,OE平分∠AOD
所以∠COF=∠BOC,∠EOD=∠AOD.
所以∠COF+∠EOD=170°,∠COF+∠EOD=170°-
又因为+2∠COF+2∠EOD+90°=360°
所以+2(170°-)+90°=360°
所以=70°,即∠COD=70°.
类型之六:与对顶角有关的记数问题
例6: O为平面上一点,过点O在这个平面上引2007条不同的直线,,,…,,则可形成________对以O为顶点的对顶角.
解析:我们知道,每两条直线相交,能形成2对对顶角,本题的关键在于推导出条这样的直线能形成多少对对顶角.
=3时,有2×3对;=4时,有3×4对;…;条直线应有对.即条直线可产生对顶角对.
当=2007时,可形成2007(2007-1)=4026042对对顶角.
一、判断题.
1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.( )
2.平面内,一条直线不可能与两条相交直线都平行.( )
3.两条直线被第三条直线所截,内错角的对顶角一定相等.( )
4.互为补角的两个角的平行线互相垂直.( )
5.两条直线都与同一条直线相交,这两条直线必相交.( )
6.如果乙船在甲船的北偏西35°的方向线上, 那么从甲船看乙船的方向角是南偏东规定35°.( )
二、填空题
1.a、b、c是直线,且a∥b,b⊥c,则a与c的位置关系是________.
2.如图(11),MN⊥AB,垂足为M点,MN交CD于N,过M点作MG⊥CD,垂足为G,EF 过点N点,且EF∥AB,交MG于H点,其中线段GM的长度是________到________的距离, 线段MN的长度是________到________的距离,又是_______的距离,点N到直线MG 的距离是___.
(11) (12)
3.如图(12),AD∥BC,EF∥BC,BD平分∠ABC,图中与∠ADO相等的角有_______ 个,分别是___________.
4.因为AB∥CD,EF∥AB,根据_________,所以_____________.
5.命题“等角的补角相等”的题设__________,结论是__________.
6.如图(13),给出下列论断:①AD∥BC:②AB∥CD;③∠A=∠C.
以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.
(13) (14) (15)
7.如图(14),直线AB、CD、EF相交于同一点O,而且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC=______度.
8.如图(15),直线a、b被C所截,a⊥L于M,b⊥L于N,∠1=66°,则∠2=________.
三、选择题.
1.下列语句错误的是( )
A.连接两点的线段的长度叫做两点间的距离
B.两条直线平行,同旁内角互补
C.若两个角有公共顶点且有一条公共边,和等于平角,则这 两个角为邻补角
D.平移变换中,各组对应点连成两线段平行且相等
2.如图,如果AB∥CD,那么图中相等的内错角是( )
A.∠1与∠5,∠2与∠6; B.∠3与∠7,∠4与∠8;
C.∠5与∠1,∠4与∠8; D.∠2与∠6,∠7与∠3
3.下列语句:①三条直线只有两个交点,则其中两条直线互相平行; ②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直; ③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题 B.②、③是正确命题
C.①、③是正确命题 D.以上结论皆错
4.下列与垂直相交的洗法:①平面内,垂直于同一条直线的两条直线互相平行; ②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平行内, 一条直线不可能与两条相交直线都垂直,其中说法错误个数有( )
A.3个 B.2个 C.1个 D.0个
四、解答题
1.如图,是一条河,C河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少 (本图比例尺为1:2000)
2.如图,ABA⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DE平行吗 为什么
3.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗 说明理由.
(2)AD与BC的位置关系如何 为什么
(3)BC平分∠DBE吗 为什么.
4.在方格纸上,利用平移画出长方形ABCD的立体图,其中点D′是D的对应点.(要求在立体图中,看不到的线条用虚线表示)
答案
一、1.× 2.∨ 3.× 4,.× 5.× 6.∨
二、
1. 互相垂直
2.点M,直线CD 点M,直线EF 平行线AB、EF间 线段GN的长度
3.4个 ∠EOB、 ∠DOF、∠ABD、∠CBD
4.两条直线都与第三条直线平行,这两条直线也互相平行 CD∥EF
5.两个角是相等两角的补角 这两个角相等
6.如果一个四边形的两组对边平行,那么它的对角相等;或若一个四边形的一组对边平行,一组对角相等,那么它的另一组对边也互相平行
7.156 8.114°
三、1.C 2.D 3.A 4.D
四、1. 略
2.(1)CD∥AB
因为CD⊥MN,AB⊥MN,
所以CDN=∠ABM=90°
所以CD∥AB
(2)平行
因为∠CDN=∠ABN=90°,∠FDC=EBA
所以∠FDN=∠EBN
所以FD∥EB
3.(1)平行
因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义)
所以∠1=∠CDB
所以AE∥FC( 同位角相等两直线平行)
(2)平行,
因为AE∥CF,
所以∠C=∠CBE(两直线平行, 内错角相等)
又∠A=∠C 所以∠A=∠CBE
所以AF∥BC(两直线平行,内错角相等)
(3) 平分
因为DA平分∠BDF,
所以∠FDA=∠ADB
因为AE∥CF,AD∥BC
所以∠FDA=∠A=∠CBE,∠ADB=∠CBD
所以∠EBC=∠CBD
4.略
1、 选择题(每题3分,共15分)
1. 下列各图中,与是对顶角的是( )
2. 直线a、b、c相交于点O,则图中对顶角共有( )
A.6对 B.5对 C.4对 D.3对
3. 下列结论中,错误的是( )
A.同一个角的两个邻补角是对顶角 B.对顶角相等,相等的两个角也是对顶角
C.对顶角的平分线在一条直线上 D.邻补角的平分线互相垂直
4. 点P是直线l ,点 A、B、C 为直线l上三点,PA=5cm,PB=4cm,PC=3cm,则点P到直线l的距离( )
A.等于4cm B.等于3cm C.小于3cm D.不大于3cm
5. 如图,下列说法中错误的是( )
A.是同位角
B.是同旁内角
C.是同位角
D.是内错角
二、填空题(每空3分,共30分)
6. 直线AB、CD相交于点O,OA平分,.则.
7. 直线AB、CD、EF相交于点O,且,,则.
8. 三角形ABC中,,cm ,cm,cm.那么点B到直线 AC的距离是___________,A、B两点的距离是________.
9. 直线AB、CD相交于点O,⑴如果,那么;⑵如果的2倍大,那么.
10. 直线AB、CD、EF相交于点O,⑴的邻补角是__________________;⑵的对顶角是___________;⑶如果,那么,.
三、解答下列各题(共55分)
11. (10分)如图,点O是直线CD上一点,,,求的度数.
12. (13分)如图,AB、CD相交于点O,,,OC平分.
⑴求的度数;⑵求的度数.
13. (10分)读句画图,分别过B、C两点画AD所在直线的垂线,垂足分别是M、N,再用刻度量出
BM=____cm,CN=_____cm;根据度量结果,
你发现BM、CN有什么关系.
14. (10分)已知点O直线AB上一点,OD平分,
OE平分,试说明.
证明 :点O在直线AB上,
°( )
OD平分, OE平分,
____,( )
即.
∴( ).
15. (12分)如图⑴,已知,,试说明.
证明:∵,,
∴( )
∴ ==________°.
如图⑵,已知,,试猜想
.
说明理由.
答案:1-5BABDC
6. 70 7.50 8.8cm 10cm 9.130 ,50 10.50,130. 11.30° 12. 30° 75° 13.0.8,0.8 图略 14.平角定义 AOC 角平分线定义AOC 垂直定义 15.⑴垂直定义 BOD 180 ⑵ 180 说明略.
1.某园林局要测量形如△ABC的一块空地面积,如图5—1—10,用以计算绿化成本,现已测量出BC的长50cm,还需测量哪些量才能算出空地面积?怎样测量?
2.如图5—1—11,计划把河中的水引入一水池
C中,怎样开的渠最短?并说明根据。
3. 取一张长方形的纸片,如图5—1—12①所示,折叠一个角,记顶点A落下的位置为A’,折痕为CD;如图5—1—12②所示再折叠另一个角,使DB沿DA’方向落下,折痕为DE,试判断∠CDE的大小,并说明理由。
答案:
课时作业:
A等级
1.如图所示,∠1和∠2是对顶角的图形有( )毛
A.1个 B.2个 C.3个 D.4个
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
(1) (2) (3)
3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( ) A.62° B.118° C.72° D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°
6.如图1所示,下列说法不正确的是( )毛
A.点B到AC的垂线段是线段AB; B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段; D.线段BD是点B到AD的垂线段
(1) (2) (3)
7.如图1所示,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
8.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
9.如图2所示,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的范围是( )
A.大于acm B.小于bcm
C.大于acm或小于bcm D.大于bcm且小于acm
10.到直线L的距离等于2cm的点有( )
A.0个 B.1个; C.无数个 D.无法确定
11.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到 直线m的距离为( )
A.4cm B.2cm; C.小于2cm D.不大于2cm
B等级
1.如图4所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
(4) (5) (6)
2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
3.如图5所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
4.如图6所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.
5.对顶角的性质是______________________.
6.如图7所示,直线AB,CD相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.
(7) (8) (9)
7.如图8所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=______________.
8.如图9所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分, 且∠BOE:∠EOD=2:3,则∠EOD=________.
9.如图3所示,直线AB与直线CD的位置关系是_______,记作_______,此时,∠AO D=∠_______=∠_______=∠_______=90°.
10.过一点有且只有________直线与已知直线垂直.
11.画一条线段或射线的垂线,就是画它们________的垂线.
12.直线外一点到这条直线的_________,叫做点到直线的距离.
C等级
1. 如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
2. 如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
3.如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
4.如图所示,村庄A要从河流L引水入庄,
需修筑一水渠,请你画出修筑水渠的路线图.
5. 如图6所示,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
6.如图所示,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的 度数.
7.如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
8.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
课时作业答案
A等级
1.A 2.B 3.B 4.A 5.D 6.C 7.D 8.C 9.D 10.C 11.D
B等级
1.∠2和∠4 ∠3 2.155° 25° 155° 4.35° 5.对顶角相等 6 .125° 55° 7.147.5° 8.42°9.垂直 AB⊥CD DOB BOC COA 10.一条 11.所在直线 12.垂线段的长度
C等级
1.∠2=60° 2.∠4=36°3.∠DOG=55°
4.解:如图3所示.
5. 解:(1)∵∠AOC+∠BOC=∠AOB=180°,
∴ ∠BOC+∠BOC=180°,
∴ ∠BOC=1 80°,
∴∠BOC=135°,∠AOC=45°,
又∵OC是∠AOD的平分线,
∴∠COD=∠AOC=45°.
(2)∵∠AOD=∠AOC+∠COD=90°,
∴OD⊥AB.
6.∠BOD=120°,∠AOE=30° 7.∠BOD=72° 8.∠4=32.5°
A
C
B
D
O
2
1
3
4
图1
1
2
O
A
C
D
图3
A
C
B
D
O
2
1
图2
O
E
C
F
D
图4
A
B
A
C
B
D
O
图5
E
A
C
B
D
图6
A
B
C
D
E
O
F
图7
O
E
C
F
D
图2
A
B
A
C
B
D
图3
A
B
O
F
C
D
E
图⑴
图⑵
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第五章 相交线、平行线
第1课时 5.1 相交线、垂线 、三线八角
平面内两条直线的位置关系是“空间与图形”所要研究的基本问题,这些内容学生在前两个学段已经有所接触,本章在学生已有知识和经验的基础上,继续研究平面内两条直线的位置关系,首先研究了两条直线相交的情形,探究了两直线相交所成的角的位置和大小关系,给出了邻补角和对顶角概念,得出了“对顶角相等”的结论;垂直作为两条直线相交的特殊情形,与它有关的概念和结论是学习下一章“平面直角坐标系”的直接基础,本章对垂直的情形进行了专门的研究,探索得出了“过一点有且只有一条直线与已知直线垂直”“垂线段最短”等结论
点击一:知识点1:对顶角的概念
定义1:两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角.
定义2:一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角.如图1中,的∠1和∠2,∠3和∠4是对顶角. 无论是哪一种定义,都同样抓住了对顶角这个概念的本质特征:一是两个角有公共顶点;二是两个角的边互为反向延长线,因此说明只有两条直线相交才能产生对顶角.
说明:⑴判断两个角是否是对顶角,要看两个角是否是两条直线相交所得到的,还要看这两个角是不是有公共顶点.⑵对顶角是成对的.两条直线相交所构成的四个角中,共有两对对顶角.
点击二:邻补角的概念
定义1:两条直线相交构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角. 图2中,∠1和∠2有公共顶点O,且有一条公共边OA,另两边成一条直线,所以∠1和∠2是邻补角.
定义2:邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角.如图3中的∠1和∠2是邻补角.
对于邻补角的概念要抓住其本质特征:一是有公共顶点;二是有一条公共边;三是另一边互为反向延长线.
说明:⑴判断两个角是邻补角的关键是看这两个角的两边,其中一边是公共边,另外两边互为反向延长线.⑵邻补角是成对的,两条直线相交所构成的四个角中,有四对邻补角.
点击三:对顶角、邻补角的性质
对顶角相等,邻补角互补.
针对练习1:
1.如图所示,∠1和∠2是对顶角的图形有( )A毛
A.1个 B.2个 C.3个 D.4个
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )B
A.150° B.180° C.210° D.120°
(1) (2) (3)
3.下列说法正确的有( )B
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( ) A A.62° B.118° C.72° D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )D
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°
6.如图4所示,直线AB,CD,EF相交于点O,指出∠AOC, ∠EOB的对顶角, ∠AOC的邻补角.图中一共有几对对顶角 几对邻补角
解: ∠AOC的对顶角是∠BOD, ∠EOB的对顶角是∠AOF;∠AOC的邻补角是∠AOD, ∠BOC.图中共有6对对顶角,12对邻补角.
7.如图5,直线AB与CD相交于点O,OE平分∠AOD, ∠AOC=,求∠BOD, ∠AOE的度数.
解:∵AB与CD相交于点O (已知),
∴∠BOD=∠AOC=(对顶角相等).
∵∠AOC+∠AOD=(邻补角定义),
∴∠AOD=-=.
∵OE平分∠AOD (已知),
∴∠AO E=∠AOD =× = (角平分线定义).
点击四:垂线的定义
当两条直线相交的四个角中,有一个角是直角时,就说这两条直线是互相垂直的,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.抓住概念的三要素:两条直线;相交;一个角是直角.
说明:⑴线段与线段、线段与射线,射线与射线,线段或射线与直线垂直,特指它们所在的直线互相垂直.⑵两条直线互相垂直,则四个角为直角.反之也成立.
点击五:垂线的画法
让直角三角板的一条直角边与已知直线重合,沿直线左右移动三角板,使其另一条直角边经过已知点,沿此直角边画直线,则这条直线就是已知直线的垂线.用三角板画垂线的三个步骤:一贴;二过;三画.
注意:⑴经过直线上一点或直线外一点画已知直线的垂线,只能画出一条。
⑵如过一点画射线或线段的垂线,是指画它们所在直线的垂线,垂足有时在射线的反向延长线或线段的延长线上.
点击六:垂线的性质
第一个性质是:“过一点有且只有一条直线垂直于已知直线.”说的是垂线的存在性和唯一性,这是垂线作图的保证;垂线的第二个性质是:“垂线段最短”.它是定义“点到直线距离”这个概念的依据.
点击七:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
注意:垂线是直线;垂线段特指一条直线,是图形;点到直线的距离是指垂线段的长度,并且是一个数量,是有单位的.
针对练习2:
1.如图6所示, ∠BAC=,AD⊥BC,垂足为D,则下列结论:①AB与AC互相垂直; ②AD与AC互相垂直;③点C到AB的垂线段是线段AB; ④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.其中正确的有( )
A.2 B.3 C.4 D5
答:A.
2.如图7,直线AB,CD相交于点O,OE⊥CD, OF⊥AB, ∠DOF=,求∠BOE和∠AOC的度数.
解:∵,OE⊥CD, OF⊥AB (已知),
∴∠BOF=∠DOE=(垂直定义).
∵∠BOD=-=,
∴∠BOE=-=,
∴∠AOC=∠BOD=(对顶角相等).
3. 已知:如图1, ∠ACB=900,D是AB上一点,且∠ADC=∠BDC,写出图中互相垂直的线段,并说明理由.
解:图中互相垂直的线段有:AC⊥BC,CD⊥AB,CD⊥AD,CD⊥DB.
4. 如图2,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE, ∠1=15030′,则下列结论中不正确的是( ).
A.∠2=450 B.∠1=∠3
C. ∠AOD与∠1互为补角 D. ∠1的余角等于75030′
解:D
5.如图1所示,下列说法不正确的是( )C毛
A.点B到AC的垂线段是线段AB; B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段; D.线段BD是点B到AD的垂线段
6.下列说法正确的有( )C
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
点击八:三线八角
了解同位角、内错角、同旁内角的相关概念,在较复杂的图形中辨认同位角、内错角、同旁内角,是进一步学习平行线、四边形等后续知识的基础.
一般地:
(1)两条直线被第三条直线所截,构成八个角(简称“三线八角”),其中同位角4对,内错角2对,同旁内角2对.
(2)准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
(3)在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
(4)在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
形象感受三类角:
1.同位角的边构成形如字母“F”状。如下图,∠M与∠N为同位角。
2.内错角的边构成形如字母“Z”状。如下图,∠M与∠N为内错角。
3.同旁内角的边构成形如字母“U”状。如下图,∠M与∠N为同旁内角。
类型之一:考查余角概念
例1如图,AOB是一条直线,∠AOC=90°,∠DOE=90°,问图中互余的角有哪几对?哪些角是相等的?
【解析】 由互为余角的定义,只需找出图中和为90°的角即可.
【解答】 因为 ∠AOC=90°,∠AOB=180°,
所以 ∠BOC=90°,∠1与∠2、∠3与∠4互余.
因为 ∠DOE=90°, 所以 ∠2与∠3互余.
因为 ∠1+∠DOE+∠4=180°,∠DOE=90°,
所以 ∠1+∠4=90°.即∠1与∠4互余.
可以得到互余的角有:∠1与∠2,∠2与∠3,∠3与∠4,∠4与∠1.
因为 ∠1与∠2互余,∠2与∠3互余,
所以 ∠1=∠3(同角的余角相等).
因为∠3与∠4互余,∠3与∠2互余,
所以 ∠2=∠4(同角的余角相等).
可以得出相等的角有:∠1=∠3,∠2=∠4,∠AOC=∠DOE=∠BOC.
类型之二:考查对顶角和邻补角的定义及其性质的运用
例2:如图2所示,直线AB,CD,EF相交于点O,指出∠AOC, ∠EOB的对顶角, ∠AOC的邻补角.图中一共有几对对顶角 几对邻补角
【解析】找一个角的对顶角时,可分别反向延长这个角的两边,以延长线为边的角即是原角的对顶角.找一个角的邻补角时,可先固定一边,反向延长另一边,则由固定边和延长线组成的角即是原角的邻补角.∠AOC的邻补角应有两个,因为固定OA,反向延长OC;固定OC,反向延长OA.三条直线相交于一点,共有三组不同的两条直线相交,即AB与CD,AB与EF,CD与EF,每两组直线相交,就得到2对对顶角,4对邻补角,故有3×2对对顶角, 3×4对邻补角.
【解答】∠AOC的对顶角是∠BOD, ∠EOB的对顶角是∠AOF;∠AOC的邻补角是∠AOD, ∠BOC.图中共有6对对顶角,12对邻补角.
类型之三:考查垂线的定义和性质
例3:如图3所示, ∠BAC=,AD⊥BC,垂足为D,则下列结论:①AB与AC互相垂直; ②AD与AC互相垂直;③点C到AB的垂线段是线段AB; ④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.其中正确的有( )
A.2 B.3 C.4 D5
【解析】:根据垂直的特征:交角为直角,可得①正确, ②错误.C点到AB的垂线段应是AC,故③错误.点A到BC的距离是指线段AD的长度,故④错误. ⑤符合定义,正确,故⑥错误.
【解答】A.
类型之四:点到直线的距离
例4 如图3,OC是∠AOB的角平分线,点P是OC上一点.
(1)分别画出点P到∠AOB两边的垂线段;
(2)比较点P到∠AOB两边距离的大小;
(3)在OC上(除O,C外)任选点D,重复(1)、(2)步骤,并根据(2)的结果完成以下猜想:角平分线上的点到角两边的距离_______.
解析:根据垂线段的定义,画垂线段的实质是画垂线,
再取点P与垂足间的线段.
(1)如图4,PE,PF即为所求.
(2)点P到∠AOB两边的距离相等.
(3)相等.
类型之五:考查方程思想
例5:如图所示,由点O引出六条射线OA、OB、OC、OD、OE、OF,且AO⊥OB,OF平分∠BOC,OE平分∠AOD,若∠EOF=170°,求∠COD的度数.
【解析】:根据垂直、角平分线定义及角的和差关系可得∠EOF=∠FOC+∠COD+∠EOD,∠COF=∠BOC,∠EOD=∠AOD.
【解答】:设∠COD=.
因为OF平分∠BOC,OE平分∠AOD
所以∠COF=∠BOC,∠EOD=∠AOD.
所以∠COF+∠EOD=170°,∠COF+∠EOD=170°-
又因为+2∠COF+2∠EOD+90°=360°
所以+2(170°-)+90°=360°
所以=70°,即∠COD=70°.
类型之六:与对顶角有关的记数问题
例6: O为平面上一点,过点O在这个平面上引2007条不同的直线,,,…,,则可形成________对以O为顶点的对顶角.
解析:我们知道,每两条直线相交,能形成2对对顶角,本题的关键在于推导出条这样的直线能形成多少对对顶角.
=3时,有2×3对;=4时,有3×4对;…;条直线应有对.即条直线可产生对顶角对.
当=2007时,可形成2007(2007-1)=4026042对对顶角.
一、判断题.
1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.( )
2.平面内,一条直线不可能与两条相交直线都平行.( )
3.两条直线被第三条直线所截,内错角的对顶角一定相等.( )
4.互为补角的两个角的平行线互相垂直.( )
5.两条直线都与同一条直线相交,这两条直线必相交.( )
6.如果乙船在甲船的北偏西35°的方向线上, 那么从甲船看乙船的方向角是南偏东规定35°.( )
二、填空题
1.a、b、c是直线,且a∥b,b⊥c,则a与c的位置关系是________.
2.如图(11),MN⊥AB,垂足为M点,MN交CD于N,过M点作MG⊥CD,垂足为G,EF 过点N点,且EF∥AB,交MG于H点,其中线段GM的长度是________到________的距离, 线段MN的长度是________到________的距离,又是_______的距离,点N到直线MG 的距离是___.
(11) (12)
3.如图(12),AD∥BC,EF∥BC,BD平分∠ABC,图中与∠ADO相等的角有_______ 个,分别是___________.
4.因为AB∥CD,EF∥AB,根据_________,所以_____________.
5.命题“等角的补角相等”的题设__________,结论是__________.
6.如图(13),给出下列论断:①AD∥BC:②AB∥CD;③∠A=∠C.
以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.
(13) (14) (15)
7.如图(14),直线AB、CD、EF相交于同一点O,而且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC=______度.
8.如图(15),直线a、b被C所截,a⊥L于M,b⊥L于N,∠1=66°,则∠2=________.
三、选择题.
1.下列语句错误的是( )
A.连接两点的线段的长度叫做两点间的距离
B.两条直线平行,同旁内角互补
C.若两个角有公共顶点且有一条公共边,和等于平角,则这 两个角为邻补角
D.平移变换中,各组对应点连成两线段平行且相等
2.如图,如果AB∥CD,那么图中相等的内错角是( )
A.∠1与∠5,∠2与∠6; B.∠3与∠7,∠4与∠8;
C.∠5与∠1,∠4与∠8; D.∠2与∠6,∠7与∠3
3.下列语句:①三条直线只有两个交点,则其中两条直线互相平行; ②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直; ③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题 B.②、③是正确命题
C.①、③是正确命题 D.以上结论皆错
4.下列与垂直相交的洗法:①平面内,垂直于同一条直线的两条直线互相平行; ②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平行内, 一条直线不可能与两条相交直线都垂直,其中说法错误个数有( )
A.3个 B.2个 C.1个 D.0个
四、解答题
1.如图,是一条河,C河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少 (本图比例尺为1:2000)
2.如图,ABA⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DE平行吗 为什么
3.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗 说明理由.
(2)AD与BC的位置关系如何 为什么
(3)BC平分∠DBE吗 为什么.
4.在方格纸上,利用平移画出长方形ABCD的立体图,其中点D′是D的对应点.(要求在立体图中,看不到的线条用虚线表示)
答案
一、1.× 2.∨ 3.× 4,.× 5.× 6.∨
二、
1. 互相垂直
2.点M,直线CD 点M,直线EF 平行线AB、EF间 线段GN的长度
3.4个 ∠EOB、 ∠DOF、∠ABD、∠CBD
4.两条直线都与第三条直线平行,这两条直线也互相平行 CD∥EF
5.两个角是相等两角的补角 这两个角相等
6.如果一个四边形的两组对边平行,那么它的对角相等;或若一个四边形的一组对边平行,一组对角相等,那么它的另一组对边也互相平行
7.156 8.114°
三、1.C 2.D 3.A 4.D
四、1. 略
2.(1)CD∥AB
因为CD⊥MN,AB⊥MN,
所以CDN=∠ABM=90°
所以CD∥AB
(2)平行
因为∠CDN=∠ABN=90°,∠FDC=EBA
所以∠FDN=∠EBN
所以FD∥EB
3.(1)平行
因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义)
所以∠1=∠CDB
所以AE∥FC( 同位角相等两直线平行)
(2)平行,
因为AE∥CF,
所以∠C=∠CBE(两直线平行, 内错角相等)
又∠A=∠C 所以∠A=∠CBE
所以AF∥BC(两直线平行,内错角相等)
(3) 平分
因为DA平分∠BDF,
所以∠FDA=∠ADB
因为AE∥CF,AD∥BC
所以∠FDA=∠A=∠CBE,∠ADB=∠CBD
所以∠EBC=∠CBD
4.略
1、 选择题(每题3分,共15分)
1. 下列各图中,与是对顶角的是( )
2. 直线a、b、c相交于点O,则图中对顶角共有( )
A.6对 B.5对 C.4对 D.3对
3. 下列结论中,错误的是( )
A.同一个角的两个邻补角是对顶角 B.对顶角相等,相等的两个角也是对顶角
C.对顶角的平分线在一条直线上 D.邻补角的平分线互相垂直
4. 点P是直线l ,点 A、B、C 为直线l上三点,PA=5cm,PB=4cm,PC=3cm,则点P到直线l的距离( )
A.等于4cm B.等于3cm C.小于3cm D.不大于3cm
5. 如图,下列说法中错误的是( )
A.是同位角
B.是同旁内角
C.是同位角
D.是内错角
二、填空题(每空3分,共30分)
6. 直线AB、CD相交于点O,OA平分,.则.
7. 直线AB、CD、EF相交于点O,且,,则.
8. 三角形ABC中,,cm ,cm,cm.那么点B到直线 AC的距离是___________,A、B两点的距离是________.
9. 直线AB、CD相交于点O,⑴如果,那么;⑵如果的2倍大,那么.
10. 直线AB、CD、EF相交于点O,⑴的邻补角是__________________;⑵的对顶角是___________;⑶如果,那么,.
三、解答下列各题(共55分)
11. (10分)如图,点O是直线CD上一点,,,求的度数.
12. (13分)如图,AB、CD相交于点O,,,OC平分.
⑴求的度数;⑵求的度数.
13. (10分)读句画图,分别过B、C两点画AD所在直线的垂线,垂足分别是M、N,再用刻度量出
BM=____cm,CN=_____cm;根据度量结果,
你发现BM、CN有什么关系.
14. (10分)已知点O直线AB上一点,OD平分,
OE平分,试说明.
证明 :点O在直线AB上,
°( )
OD平分, OE平分,
____,( )
即.
∴( ).
15. (12分)如图⑴,已知,,试说明.
证明:∵,,
∴( )
∴ ==________°.
如图⑵,已知,,试猜想
.
说明理由.
答案:1-5BABDC
6. 70 7.50 8.8cm 10cm 9.130 ,50 10.50,130. 11.30° 12. 30° 75° 13.0.8,0.8 图略 14.平角定义 AOC 角平分线定义AOC 垂直定义 15.⑴垂直定义 BOD 180 ⑵ 180 说明略.
1.某园林局要测量形如△ABC的一块空地面积,如图5—1—10,用以计算绿化成本,现已测量出BC的长50cm,还需测量哪些量才能算出空地面积?怎样测量?
2.如图5—1—11,计划把河中的水引入一水池
C中,怎样开的渠最短?并说明根据。
3. 取一张长方形的纸片,如图5—1—12①所示,折叠一个角,记顶点A落下的位置为A’,折痕为CD;如图5—1—12②所示再折叠另一个角,使DB沿DA’方向落下,折痕为DE,试判断∠CDE的大小,并说明理由。
答案:
课时作业:
A等级
1.如图所示,∠1和∠2是对顶角的图形有( )毛
A.1个 B.2个 C.3个 D.4个
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
(1) (2) (3)
3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( ) A.62° B.118° C.72° D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°
6.如图1所示,下列说法不正确的是( )毛
A.点B到AC的垂线段是线段AB; B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段; D.线段BD是点B到AD的垂线段
(1) (2) (3)
7.如图1所示,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
8.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
9.如图2所示,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的范围是( )
A.大于acm B.小于bcm
C.大于acm或小于bcm D.大于bcm且小于acm
10.到直线L的距离等于2cm的点有( )
A.0个 B.1个; C.无数个 D.无法确定
11.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到 直线m的距离为( )
A.4cm B.2cm; C.小于2cm D.不大于2cm
B等级
1.如图4所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
(4) (5) (6)
2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
3.如图5所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
4.如图6所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.
5.对顶角的性质是______________________.
6.如图7所示,直线AB,CD相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.
(7) (8) (9)
7.如图8所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=______________.
8.如图9所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分, 且∠BOE:∠EOD=2:3,则∠EOD=________.
9.如图3所示,直线AB与直线CD的位置关系是_______,记作_______,此时,∠AO D=∠_______=∠_______=∠_______=90°.
10.过一点有且只有________直线与已知直线垂直.
11.画一条线段或射线的垂线,就是画它们________的垂线.
12.直线外一点到这条直线的_________,叫做点到直线的距离.
C等级
1. 如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
2. 如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
3.如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
4.如图所示,村庄A要从河流L引水入庄,
需修筑一水渠,请你画出修筑水渠的路线图.
5. 如图6所示,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
6.如图所示,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的 度数.
7.如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
8.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
课时作业答案
A等级
1.A 2.B 3.B 4.A 5.D 6.C 7.D 8.C 9.D 10.C 11.D
B等级
1.∠2和∠4 ∠3 2.155° 25° 155° 4.35° 5.对顶角相等 6 .125° 55° 7.147.5° 8.42°9.垂直 AB⊥CD DOB BOC COA 10.一条 11.所在直线 12.垂线段的长度
C等级
1.∠2=60° 2.∠4=36°3.∠DOG=55°
4.解:如图3所示.
5. 解:(1)∵∠AOC+∠BOC=∠AOB=180°,
∴ ∠BOC+∠BOC=180°,
∴ ∠BOC=1 80°,
∴∠BOC=135°,∠AOC=45°,
又∵OC是∠AOD的平分线,
∴∠COD=∠AOC=45°.
(2)∵∠AOD=∠AOC+∠COD=90°,
∴OD⊥AB.
6.∠BOD=120°,∠AOE=30° 7.∠BOD=72° 8.∠4=32.5°
A
C
B
D
O
2
1
3
4
图1
1
2
O
A
C
D
图3
A
C
B
D
O
2
1
图2
O
E
C
F
D
图4
A
B
A
C
B
D
O
图5
E
A
C
B
D
图6
A
B
C
D
E
O
F
图7
O
E
C
F
D
图2
A
B
A
C
B
D
图3
A
B
O
F
C
D
E
图⑴
图⑵
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
