第1课时平面直角坐标系及性质
文档属性
| 名称 | 第1课时平面直角坐标系及性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 502.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-17 17:57:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第六章 平面直角坐标系
第4课时 平面直角坐标系及性质
从本章知识结构来看,平面直角坐标系是全章的核心内容。由此可见,本节的知识不仅是后面坐标方法的简单应用的基础,也是后继学习函数的图像,函数与方程和不等式的关系等知识的坚实基础。
理解平面直角坐标系的有关概念,会正确地画出直角坐标系,并能在建立的平面直角坐标系中,由点的位置写出它的坐标,由坐标描出点的位置。
重点是理解平面直角坐标系的有关概念,由点的位置写出坐标,由坐标描出点的位置。
难点是由点的位置写出坐标,并让学生形成数形结合的意识。
点击一:用有序数对表示平面上物体的位置:
物体在平面内的位置需从横向和纵向两个方面来确定,因此可以利用有序数对来准确的表示物体的位置。此时一般用表示物体的横向位置,用来表示物体的纵向位置。如电影票的号码是第8排第6号,我们可以根据一对整数(8,6)便很快找到座位等。
点击二:点的坐标:
(1)点的坐标:平面内的任意一点都可以用一个有序数对来表示,这个有序数对就叫做这个点的坐标。如图1点A
可以用有序数对(3,4)表示,3叫做
点A的横坐标,4叫做点A的纵坐标,
有序数对(3,4)叫做点A的坐标。
反过来,每一个有序数对对应着平面内的
一个点,如有序数对(-3,-4)表示点B。
(2)由点求其坐标、由坐标定点的方法:
由点求其坐标是:由此点向作垂线,
根据垂足的坐标来确定各点的横坐标和纵坐标。
由坐标定点是:先在上找到表示横坐标的点,再在上找到表示纵坐标的点,过这两个点分别作的垂线,则垂线的交点就是所要画的点。
点击三:平面直角坐标系的组成:
平面直角坐标系是由两条互相垂直且有公共原点的数轴组成。平面直角坐标系将平面分成了以下六个部分:、两坐标轴正方向所夹的部分称为第一象限,从第一象限开始沿逆时针方向分别为:第一象限、第二象限、第三象限、第四象限。六个部分除了有一公共的交点(原点)以外,其他区域之间均没有公共点。
点击四:坐标平面内点的特征:
1.各象限内点的坐标的符号特征:
第一象限(+,+); 第二象限(-,+); 第三象限(-,-); 第四象限(+,-);
2.坐标轴上点的坐标的特征:
的正半轴(+,0);的负半轴(-,0);的正半轴(0,+);的负半轴(0,-)。
3.坐标原点O的坐标为(0,0)。
针对练习1:
1.已知坐标平面内点A(m、n)在第四象限,那么点B(n、m)在()
A,第一象限 B,第二象限 C,第三象限 D,第四象限
2.已知点M(1-a,a +2)在第二象限,则a的取值范围是()
A,a>-2 B,-2<a<1 C,a<-2 D,a>1
3.点P(m +3,m +1)在直角坐标系的x轴上,则P点坐标为()
A,(0,-2) B,(2,0) C,(0,2) D,(0,-4)
4.若0<m<2,则点P(m-2,m)在()
A,第一象限 B,第二象限 C,第三象限 D,第四象限
5.在直角坐标系xOy中,已知A(2,-2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有()
A,2个 B,3个 C,4个 D,5个
6.如果代数式有意义,那么,直角坐标系中点P(m,n)的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在直角坐标系中,A(1,2)点的横坐标乘以-1,纵坐标不变,得到A’点,则A与A’的关系是( )
A.关于x轴对称; B.关于y轴对称;
C.关于原点对称; D.将A点向x轴负方向平移一个单位
8.如图6所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点 ( )
A,(-1,1) B,(-1,2) C,(-2,1) D,(-2,2)
9.若A(a,6),B(2,a),C(0,2)三点在同一条直线上,则a的值为( )
A,4或-2 B,4或-1 C,-4或1 D,-4或2
10.点P(m,1)在第二象限内,则点Q(-m,0)在( )
A,x轴正半轴上 B,x轴负半轴上 C,y轴正半轴上 D,y轴负半轴上
11.点A(,)在第三象限,则的取值范围是( )
A. B. C. D.
答案:1,B;2,D;3,B;4,B;5,C; 6,C;7,B;8,C;9,A;10,A;11,C.
类型之一:体现新课标理念的规律探究型题
例1:一个质点在第一象限及轴、轴上运动,在第一秒钟,它从原点运动到,然后接着按图1中箭头所示方向运动[即 ( http: / / www.21cnjy.com / )],且每秒移动一个单位,那么第35秒时质点所在位置的坐标是( )
A. B. C. D.
解析:这是一道以平面直角坐标系点的坐标为载体的规律探究型问题. 根据条件“按图中箭头所示方向运动,且每秒移动一个单位”我们来看质点从内到外移动到每一个长方形的端点时的时间与坐标变化规律:
第3秒时质点所在位置的坐标是(1,0);
第8(3+5=8)秒时质点所在位置的坐标是(0,2);
第15(8+7=15)秒时质点所在位置的坐标是(3,0);
第24(15+9=24)秒时质点所在位置的坐标是(0,4);
第35(24+11=35)秒时质点所在位置的坐标是(5,0)
解答:选B.
评注:此题若是根据条件硬推则也能得到答案,但就方法显得拙笨.但我们这里根据规律还可知道:第48(35+13=48)秒时质点所在位置的坐标是(0,6);第63(48+15=63)秒时质点所在位置的坐标是(7,0)等.
练习:如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第个点的坐标为____________.(答案:(14,8))
类型之二:考查接受新问题能力的新定义概念题
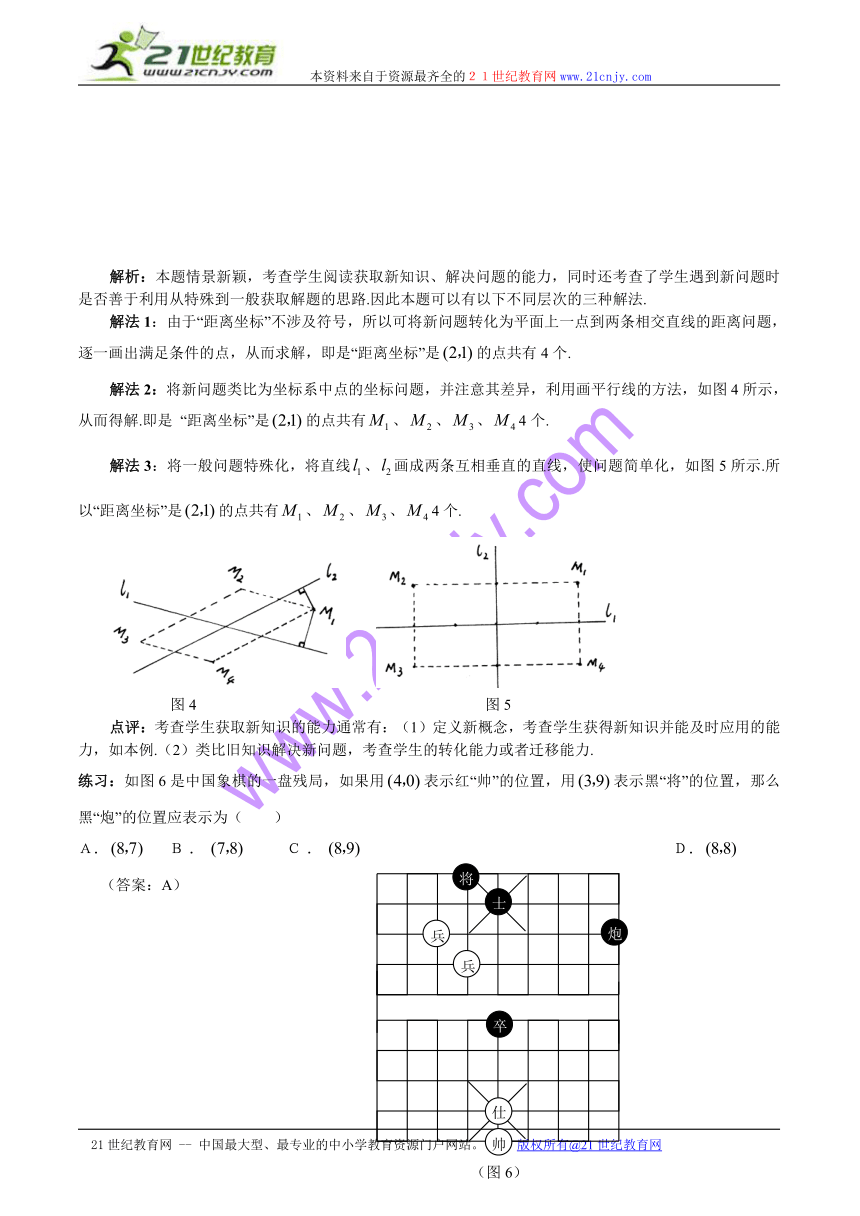
例2:如图3,在平面内,两条直线,相交于点,对于平面内任意一点,若分别是点到直线,的距离,则称为点的“距离坐标”.根据上述规定,“距离坐标”是的点共有 个.
解析:本题情景新颖,考查学生阅读获取新知识、解决问题的能力,同时还考查了学生遇到新问题时是否善于利用从特殊到一般获取解题的思路.因此本题可以有以下不同层次的三种解法.
解法1:由于“距离坐标”不涉及符号,所以可将新问题转化为平面上一点到两条相交直线的距离问题,逐一画出满足条件的点,从而求解,即是“距离坐标”是的点共有4个.
解法2:将新问题类比为坐标系中点的坐标问题,并注意其差异,利用画平行线的方法,如图4所示,从而得解.即是 “距离坐标”是的点共有、、、4个.
解法3:将一般问题特殊化,将直线、画成两条互相垂直的直线,使问题简单化,如图5所示.所以“距离坐标”是的点共有、、、4个.
( http: / / www.21cnjy.com / )
图4 图5
点评:考查学生获取新知识的能力通常有:(1)定义新概念,考查学生获得新知识并能及时应用的能力,如本例.(2)类比旧知识解决新问题,考查学生的转化能力或者迁移能力.
练习:如图6是中国象棋的一盘残局,如果用表示红“帅”的位置,用表示黑“将”的位置,那么黑“炮”的位置应表示为( )
A. B. C. D.
(答案:A)
类型之三: 在平面直角坐标系中确定点的位置:
例3:已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),I(3,-2),J(2,0),K((3,2),L(1,1).
(1)请在如图所示的平面直角坐标系中,分别描出上述各点,并顺次连结;
(2)试求(1)中连线围成图形的面积.
解析:第(1)小题,依据点的横、纵坐标的定义,分别描出各点并依次连结;第(2)小题,图形被坐标轴平均分成四部分,故只要查出一个象限中图形围起的小正方形的个数,就可求得答案.
解:(1)如右图所示,
(2)∵第一象限中图形围起的小正方形个数为(4-2×-2×)+(3-2×)=4,∴第一象限中图形围起的小正方形的总面积为12×4=4.
∵图形被坐标轴平均分成四部分,∴图形的总面积为4×4=16.
点拨:结合点的坐标与图形中线段长度的意义,合理分割图形、找准小正方形的个数是解答第(2)小题的关键.
类型之四:根据条件判断点所属象限:
例4:已知(a-2)2+(b+3)2=0,试判断点M(-a,-)所在的象限.
分析:由(a-2)2+(b+3)2=0,得a=2,b=-3,所以点M(-2,-)在第三象限.
解:由(a-2)2+(b+3)2=0,得a=2,b=-3,∴-a=-2,-=-,即点M的坐标为(-2,-),又∵-2<0,-<0,∴点M(-a,-)在第三象限.
类型之五:平移在平面直角坐标系中的应用:
例5:如图,三角形A1B1C1是由三角形ABC平移后得到的,三角形ABC中任意一点M(x0,y0)经平移后对应点为M1(x0-5,y0-3),求A1、B1、C1、的坐标,并求出三角形A1B1C1的面积.
分析:观察两个三角形的平移过程,由M(x0,y0)和M1(x0-5,y0-3)可知:三角形A1B1C1是由三角形ABC先向下平移3个单位长度,再左平移5个单位长度,即可求出A1、B1、C1、的坐标,而三角形A1B1C1的面积可以看做是一个长方形的面积减去一些小三角形的面积.
解:由M(x0,y0)和M1(x0-5,y0-3)可知:三角形A1B1C1是由三角形ABC先向下平移3个单位长度,再左平移5个单位长度,相应地,三角形A1B1C1的各个顶点坐标,也是由三角形ABC各个顶点坐标先向下平移3个单位长度,再向左平移5个单位长度,即三角形A1B1C1的各个顶点坐标分别为:A1(-2,3)、B1(-4,-1)、C1(1,1).从三角形A1B1C1的各个顶点构造一个长方形B1DEF,则三角形A1B1C1的面积=长方形B1DEF-三角形A1B1D的面积-三角形A1C1E的面积-三角形B1C1F的面积=5×4-×2×4-×2×3-×2×5=8.
点拨:用坐标表示平移:①平移规律:
②一个图形进行平移,这个图形上所有的点的坐标都要发生相应的变化;反过来,如果图形上的点的坐标发生变化,那么这个图形进行了平移;③平移特征:一个图形平移前后大小、形状完全相同,只是位置不同.同时,还要知道:在坐标系中求一个图形的面积,一般要把它转化为一些能用面积公式表达的图形的和与差来求解,如在本题中所求的三角形面积可以看做一个长方形的面积减去一些小三角形的面积来求解.
1、 填空题
1、 在坐标平面内点的位置与有序实数对是 对应。
2、 点P(a,b)在y轴的正半轴上,则a b
3、 已知点P在第三象限,且到x轴的距离是2,到y轴的距离是3,则点P的坐标为 。
4、 按下列条件确定点为P(x,y)的位置:(1)xy=0,则点P一定在 (2)若x2十y2=0,则点P在
5、 若M点的坐标是(a,一3)N点的坐标(2,b)且点M与点N关于x轴对称则a= b=
6、 已知点A在x轴上,且点A到原点的距离为4个单位,则点A的坐标是
二选择题
1、点P(一3,4)关于y轴对称点的坐标是( )
A(3,一4 ) B(一3,一4) C(3,4) D(一4,一3)
2、点B与点C的横坐标相同,纵坐标不同,则直线BC与x轴的关系为( )
A平行 B垂直 C斜交 D以上都不正确
3、A,B是同一坐标轴上的两个点,A点坐标是(一2,0)A与B的距离是5,则B点的坐标为( )
A(3,0) B(一7,0)
C(3,0)或(一7,0) D(一3,0)或(7,0)
4、以边长为4的正方形的对角线建立直角坐标系,其中一个顶点位于y轴的负半轴上,则该点坐标为( )
A(2,0) B(0,一2)
C(0,2) D(0,一2 )
5、己知M(a,b)在坐标轴上,则a,b满足( )
A、 a=0, B、b=0, C、a=0且b=0, D、ab=0
6、直角坐标系中,点P(x,y)在第三象限,且P到x轴,y轴距离分别为3,7。则P点的坐标为()
A(一3,一7),B(一7,一3),C(3,7)D(7,3)
7、已知A、B两点的连线平行于x轴,y轴,则A、B的坐标之间的关系是( )
A横坐标相同 B纵坐标相同 C横坐标的绝对值相同 D纵坐标的绝对值相同
8、如果P(m十3,2m十4)在y轴上,那么点P的坐标( )
A(一2,0)B(0,一2)C(1,0)D(0,1)
三、解答题
1、 如图为画在方格纸上的花坛设计简图,
(1) 请写出图中平行四边形ABCD各个顶点的坐标。在图中A与D,B与C的纵坐标相同吗?为什幺?
(2) A与B,C与D的横坐标相同吗?为什么?
2、如图三角形AOB中,A,B两点的坐标分别为(2,4)(6,2)求三角形AOB的面积。
3、 己知矩形ABCD中AB=4,BC=6这AB//x轴,若点A的坐标为(一1,2)求C点的坐标。
4、如图菱形ABCD的中心在直角坐标系的原点,一条边AD与x轴平行,己知点A,D的坐标分别是(一4,3)(,3)求B、C的坐标。
(提示:A、C;B,D关于原点对称)
5.下面是某小区的公共设施图,请你建立适当的直角坐标系,写出各处的坐标。
6.如图△ABC与△关于y轴对称,根据图形的位置写出△ABC与△各顶点的坐标
思考:关于y轴对称的两个图形的对应顶点的坐标有什么关系?
参考答案
一、1、一一对应
2、=0,>0
3、(-3,-2)
4、x轴或y轴包括原点,原点
5、2,3
6、(4,0)或(-4,0)
二、1、C2、B3、B4、C5、D6、A7、B8、B
三、1、(1)A(-3,4)B(-6,-3)C(4,-3)D(7,4)A与D,B与C的纵坐标相同(2)不相同因为不平行于y轴
2、10
3、(3,8)(-5,8)
4、B()C(4,一3)
5、略
6、A(0.5,0)B(3,2)C(2,4)A’(一0.5,0)B’(一3,2)C’(一2,4)关于y轴的两个图形的顶点的横坐标互为相反数,纵坐标不变。
一.选择题
1.如图1所示,一方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B 的位置是 ( )毛
A. (4, 5); B.(5,4); C.(4,2); D.(4,3)
2.如图1所示,B左侧第二个人的位置是 ( )
A.(2,5); B.(5,2); C.(2,2); D.(5,5)
3.如图1所示,如果队伍向西前进,那么A北侧第二个人的位置是 ( )
A.(4,1); B.(1,4); C.(1,3); D.(3,1)
4.如图1所示,(4,3)表示的位置是 ( )
A.A B.B C.C D.D
5.如图2所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
6.如图2所示,横坐标和纵坐标都是负数的点是 ( ) A.A点 B.B点 C.C点 D.D点
7.如图2所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
8.若点M的坐标是(a, b),且a>0,b<0,则点M在( )
A.第一象限;B.第二象限; C.第三象限;D.第四象限
二.填空题
1.如图2所示,进行“找宝”游戏,如果宝藏藏在(3,3)字母牌的下面, 那么应该在字母______的下面寻找.
2.如图3所示,如果点A的位置为(3,2),那么点B的位置为______, 点C 的位置为______,点D和点E的位置分别为______,_______.
3.如图4所示,如果点A的位置为(1,2),那么点B的位置为_______,点C 的位置为_______.
4.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
5.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
6.在坐标平面内,已知点A(a, b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
7.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
8.已知点M(a, b),当a>0,b>0时,M在第_______象限;当a____, b______时,M 在第二象限;当a_____, b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
三.
1.如图所示,A的位置为(2,6),小明从A出发,经
(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经
(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
2. 如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法
3. 如图所示,四个正方形组成一个“T”字形,你能用四个这样的图形拼成一个正方形吗
4. 如果点A的坐标为(a2+1,-1-b2),那么点A在第几象限 为什么
5. 如果点A(t-3s,2t+2s),B(14-2t+s,3t+2s-2)关于x轴对称,求s, t的值.
6. 如图所示,C,D两点的横坐标分别为2,3,线段CD=1;B,D两点的横坐标分别为-2,3,线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1 (2)如果y轴上有两点P(0,y1),Q(0,y2)(y1 7. 如果│3x-13y+16│+│x+3y-2│=0,那么点P(x, y)在第几象限 点Q(x+1,y-1)在坐标平面内的什么位置
8. 如图4所示,图中的能走遍棋盘中的任何一个位置吗 若不能,指出哪些位置无法走到;若能,请说明原因.
答案:
一.1.A 2.A 3.B 4.C 5.B 6.C 7.D 8.D
二.1.M 2.(0,1) (1,3) (2,5) (2,1) 3.(0,1) (-1,0)4.(-1,2) (-1,-2) (1,-2) 5. (4,6) (-4,-6)
6.(a,-b) (-a,b) 7. 二 四 一 三 y x 8.一 <0 >0 >0 <0 三
三.1.3个格. 2. 解:如图所示的是最短路线的6种走法.
3. 解:如图所示.毛
4. 解:∵a2+1>0,-1-b2<0,
∴点A在第四象限.
5. 解:∵关于x轴对称的两个点的横坐标相等,纵坐标互为相反数,
∴
即,两式相加得8t=16,t=2.
3×2-4s=14,s=-2.
6. 解:(1)MN=x2-x1 (2)PQ=y2-y1
7. 解:根据题意可得3x-13y+16=0,x+3y-2=0,
由第2个方程可得x=2-3y,
∴第1个方程化为3(2-3y)-13y+16=0,
解得y=1,x=2-3y=-1,
∴点P(x,y),即P(-1,1) 在第二象限,Q(x+1,y-1),
即Q(0,0)在原点上.
8. 提示: 能走遍棋盘中的任何一个位置,
只需说明 能走到相邻的一个格点即可.毛
1.如图7,把矩形OABC放置在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF.
(1)可以通过________办法,使四边形AEFO变到四边形BEFC的位置(填“平移”、“旋转”或“翻转”);
(2)求点E的坐标;
(3)若直线l把矩形OABC的面积分成相等的两部分,则直线l必经过点的坐标是_____.
2.如图8,在平面直角坐标系中,已知点为A(-2,0),B(2,0).
(1)画出等腰三角形ABC(画出一个即可);
(2)写出(1)中画出的ABC的顶点C的坐标.
3.如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.如图9,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…….对称中心分别是A、B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标.
答案:1.(1)旋转,(2)(6,),(3)(3,4);2.略;3.P2(1,-1) ,P7(1,1) ,P100(1,-3).
课时作业:
A等级
一、填空题
1、若点P(10一2a,3一b)的横坐标是正数,纵坐标是负数,则a b
2、巳知,则点(x,y)在 象限。
3、若Rt△ABC的各顶点坐标分别是A(0,一4),B(3,0)C(0,0)则△ABC的各边长是AC= BC= AB= △ ABC的面积
4、将△ABC绕坐标原点旋转后,各顶点坐标变化特征是
二.选择题
1、到x轴的距离是3且到y轴的距离是4的点有( )
A1个 B2个 C3个 D4个
2、 菱形ABCD的两条对角线分别是8和6,以对角线AC,BD的交点O为坐标原点,AC所在直线为横轴,建立直角坐标系,则A点的坐标可能是( )
A(0,一4)B(0,一3)C(0,4)D(一4,0)
3、己知A、B两点的连线平行于x轴,则A、B的坐标之间的关系是()
A、 横坐标相同B、纵坐标相同C、横坐标的绝对值相同D、纵坐标的绝对值相同
三、解答题
1、 若有序数对(3,a)(b,5)所在的两点连线与水平方向垂直且两点不重合,则a,b应满足的条件?
2、 假设我们约定“列数在前,排数在后”那么下列五位学生的座位自前至后的排列是
A(5,9)B(3,2)C(4,3)D(2,8)E(1,6)若“排数在前,列数在后”呢?
3、 在直角坐标系内,将坐标为(1,1)(2,1)(2,2)(1,2)(1,3)(2,3)的点依次连结起来,组成一个图形。
(1) 横坐标,纵坐标分别乘以一1呢?
(2) 横坐标不变,纵坐标乘以一1呢?
4、 在直角坐标系中描出下列各点,并将各组内的点用线段依次连接起来。
a、(5,1)(5,3)(1,3)(1,7)(5,7)(5,8)(7,8)(7,7)(11,7)(11,3)(7,3)(7,1)(5,1)
b、(5,4)(3,4)(3,6)(5,6)(5,4)
c、(7,4)(7,6)(9,6)(9,4)(7,4)
(1) 观察所得图形,你觉得他象什么?
(2) 纵坐标保持不变,横坐标分别乘以一1,所得图案与原来的图案相比有什么变化?
B等级
1. 已知点,是轴上的点,则.
2. 已知直线平行于轴,且点坐标为,,则点坐标为 ,条件 .
3. 若点,在第一、三象限角平分线上,求的值.
4. 已知两点,,,,若轴,求的值,并确定.
5. 已知点坐标为,,且点到两坐标轴距离相等,求点坐标.
6. 如图,点的坐标是 ,点的坐标是 ,点的坐标是 ,坐标是的点是 ,坐标是的点是 ,点的坐标是对吗? .(填“对”“不对”,并填出正确答案)
7 写出图中所标出的各点的坐标.
8. 已知点在第二象限,它的横坐标与纵坐标的和为1,则点的坐标是 (写出符合条件的一个点即可).
9. 如图,是某市几个单位的示意图(图中每个小正方形的边长为1个单位长度),请以某一个单位为原点,画出平面直角坐标系,并写几个单位的坐标.
10. 若点,在第四象限,则,.
11. 若点的横坐标是-3,纵坐标是2,则点的坐标记作 ,点在第 象限.
12. 若点,在第二象限,则点,在第 象限.
13. 若点,是第二象限内的点,则必须满足 .
14. 若点,在第二象限,,在第三象限,则点,在第 象限.
15. 下列各点:,,,,,,,,,,,中,位于第一象限的有 ,位于第三象限的有 ,位于坐标轴上的有 .
16. 设点的坐标为,,根据下列条件,判定点在坐标平面内位置:
⑴;⑵;⑶.
17. 如果点,在第一象限,那么点,在 ( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
18. 已知点,,下列说法正确的有 ( )
A.当时,点在轴上 B.当时,点在轴上
C.当时,点在第一或第四象限 D.当时,点在轴左方
19. 按下列条件确定点,的位置:
⑴,,则点在 .
⑵,则点一定在 .
⑶若,则点在 .
20. 如果点,在第二象限,那么点,在第 象限.
21. 已知点,在轴的负半轴上,则点,在( )
A.第一象限 B.第二象限 C.第三角限 D.第四象限
22. 已知点,,且,则点在 ( )
A.原点 B.轴上 C.轴上 D.坐标轴上
23. 平行于轴的一条直线上的点的横坐标一定 ( )
A.大于0 B.小于0 C.相等 D.相反
24. 已知点,关于轴的对称点是 ,关于轴的对称点是 ,关于原点的对称点是 .
25. 点,关于轴的对称点的坐标是 ( )
A., B., C., D.,
26. 已知点,,,,如果,,那么点,( )
A.关于原点对称 B.关于轴对称
C.关于轴对称 D.关于过点(0,0),(1,1)的直线对称
C等级
1. 在坐标平面内点的位置与有序实数对 对应.
2. 如图所示的马所处的位置为(2,3).
⑴你能表示图中象的位置吗?
⑵写出马的下一步可以到达的位置.
3. 有序数对的意义是 ,利用有序数对,可以很准确地 .
4. 如果约定街在前,巷在后,则某单位在5街2巷的十字路口,用有序数对表示为( )
A.(2,5) B.(5,2) C.(5,5) D.(2,2)
5. 如图,写出表示下列各点的有序数对:
(_,_);(5,2);(_,_);(_,_);(_,_);(_,_);(_,_);(_,_);(_,_);
6. 如图,表示下列图形格点的有序数对.
(1,4)( )( )( )( )( )( )
7. 有序数对(2,3)和(3,2)相同吗?如果有序数对,表示某栋楼房中层楼号房,那么有序数对(2,3)和(3,2)分别代表什么?
8. 如图,甲处表示三街与二巷的十字路口,乙处表示六街与六巷的十字路口,如果用(3,2)表示甲处位置,那么(3,2)→(3,3)→(3,4)→(3,5)→(3,6)→(4,6)→(5,6)→(6,6)表示从甲处到乙处的一条路线,请你用有序数对写出其他几种从甲处到乙处的路线.
9 为了用一对实数表示平面内的点,在平面内画两条互相垂直的数轴,组成了 ,水平的数轴叫做 ,取 为正方向,铅直的数轴叫做 ,取 为正方向.
10. 画平面直角坐标系,标出下列各点:
点在轴上,位于原点上方,距离原点2个单位长度;
点在轴上,位于原点右侧,距离原点1个单位长度;
点在轴上方,轴右侧,距离每条坐标轴都是2个单位长度;
点在轴上,位于原点右侧,距离原点3个单位长度;
点在轴上方,轴右侧,距离轴2个单位长度,距离轴4个单位长度,依次连接这些点,你能得到什么图形?
11. 如图,正方形的边长为2,建立适当的平面直角坐标系,分别表示,,,四个点的坐标.
12. 如图是画在方格纸上的某一小岛的示意图.
⑴分别写出地点,,,,的坐标;
⑵(3,6),(7,9),(8,7),(3,3)所代表的地点分别是什么?
13. 在如图所示的坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
⑴(1,2),(2,1),(6,1),(7,3);
⑵(3,3),(3,6),(5,2.5);
观察所得到的图形,你觉得它像什么?
14. 点的坐标是,则是点的 ,是点的 ,点在第 象限.
15. 已知点到轴、轴的距离分别为2和,若点的横坐标、纵坐标都是正值,则点坐标是 .
16. 点位于轴左方,距轴3个单位长,位于轴上方,距轴四个单位长,点的坐标是 ( )
A. B. C. D.
17. 在直角坐标系中,点,在第二象限,且到轴、轴距离分别为3,7,则点坐标为( )
A. B. C. D.
18. 已知点(1,2),轴于,则点坐标为 ( )
A.(2,0) B.(1,0) C.(0,2) D.(0,1)
19. 已知点,满足,则点的位置是 ( )
A.在轴或轴上
B.在第一、三象限坐标轴夹角平分线上
C.在第二、四象限坐标轴夹角平分线上
D.在坐标轴夹角平分线上
20. 正方形中,,,坐标分别是,,,则顶点坐标是 .
21. 自画一个坐标系并描出下列各点:
(2,1),(-2,1),(4,-3),(4,3),(-3,-2),(3,2),(0,-1),(,0).
根据在坐标系中描出的点观察:与,与,与在位置上有何特点?并说明它们纵、横坐标各有什么特点.
22. 如图,在所给的坐标系中描出下列各点的位置:
,,,,,.
你发现这些点有什么关系?你能再找出一些类似的点吗?
23. 在方格纸上建立一个平面直角坐标系,描出点,,连接,若点为直线上的任意一点,则点的纵坐标是什么?
⑴如果一些点在平行于轴的直线上,那么这些点的纵坐标有什么特点?
⑵如果一些点在平行于轴的直线上,那么这些点的横坐标有什么特点?
24. 在下图所示的直角坐标系中描出下列各点:
,;,;,;,;,;,;,;,;,;,;,.
依次连结各点,观察得到的图形,你觉得它像什么?
25. 李强同学家在学校以东100m再往北150m处,张明同学家在学校以西200m再往南50m处,王玲同学家在学校以南150m处,如图,在坐标系中画出这三位同学家的位置,并用坐标表示出来.
26. 根据下图填表.
点 坐标 象限或坐标轴
课时作业答案;
A等级答案:
一1、 <3, >3
2 、 一
3、4,3,5,6 ;
4、横坐标纵坐标均为相反数
二
1 、D 2 、D3、B
三、
1、b=3,
2、BCEDA,EDBCA
3、(1)所得的图形被横向拉长了一倍
(2)所得的图形向y轴正方向平移了3个单位
(3)所得的图形与原图形关于原点对称
(4)所得的图形与原图形关于x轴对称
4、(1)“中”字(2)关于y轴的对称图案。
B等级答案
1:.2:,,.3:.4:,.5:,.
6:;;;点;点;不对..
7:;;;;;;.
8:有无数个.例如:.9:略.10:>,<.11:,二.12:四.13:.
14:三.15:,;;,.
16:⑴坐标轴上;⑵点在第一或第三象限;⑶点在第二或第四象限.
17:C.18:D.19:⑴轴的负半轴上;⑵坐标轴上;⑶原点.20:三.21:B.22:A.
23:C.24:,,.25:A.26:D.
C等级答案
1:一一.2:⑴ 象的位置(5,3);
⑵马的下一步可到达位置(1,1)(3,1)(4,2)(1,5)(3,5).
3:有顺序的两个数与组成的数对记为;表示一个位置.4:B.
5:(3,3);(5,2);(7,3);(10,3);(10,5);(7,7);(5,7);(3,6);(4,8).
6:(1,4);(3,1);(7,1);(9,2);(8,4);(6,3);(4,6).
7:不同.2层楼3号房;3层楼2号房.8:略.9:平面直角坐标系;轴,向右;轴,向上.10:略.11:略.12:⑴(2,9);(5,8);(5,5);(7,4);(8,1);⑵分别代表点:,,,.13:略.14:横坐标,纵坐标,三.15:(,2).16:B.17:B.18:B.19:D.20:.21:略.
22:这些点都在过原点经过一、三象限的一条直线上,且这条直线上的任意一个点到轴、轴距离相等.能找很多:(1,1),(0.2,0.2).
23:点纵坐标为4.⑴都相等;⑵都相等24:像五角星.25:李强家;张明家;王玲家.26:略.
A
B
C
O
E
F
x
y
图7
图6
O
(1,0)
(2,0)
(3,0)
(4,0)
(5,0)
x
(5,1)
(4,1)
(3,1)
(2,1)
(3,2)
(4,2)
(4,3)
(5,4)
(5,3)
(5,2)
y
图2
0
1
2
3
x
y
1
2
3
…
图1
图3
将
士
炮
卒
仕
帅
兵
兵
(图6)
A′(x+a,y)或(x-a,y)
B′(x,y+b)或(x,y-b)
向右或向左平移
a个单位
向上或向下平移
b个单位
点A(x,y)
A
B
C
O
E
F
x
y
图7
图8
图9
体育馆
广场
学校
商场
幼儿园
1
2
3
4
5
2
3
4
5
6
7
8
9
象
马
0
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
10
一巷
二巷
三巷
四巷
五巷
六巷
七巷
一街
二街
三街
四街
五街
六街
七街
八街
甲
乙
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
1
2
3
1
2
3
北
东
单位:m
0
50
50
1
2
3
4
5
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第六章 平面直角坐标系
第4课时 平面直角坐标系及性质
从本章知识结构来看,平面直角坐标系是全章的核心内容。由此可见,本节的知识不仅是后面坐标方法的简单应用的基础,也是后继学习函数的图像,函数与方程和不等式的关系等知识的坚实基础。
理解平面直角坐标系的有关概念,会正确地画出直角坐标系,并能在建立的平面直角坐标系中,由点的位置写出它的坐标,由坐标描出点的位置。
重点是理解平面直角坐标系的有关概念,由点的位置写出坐标,由坐标描出点的位置。
难点是由点的位置写出坐标,并让学生形成数形结合的意识。
点击一:用有序数对表示平面上物体的位置:
物体在平面内的位置需从横向和纵向两个方面来确定,因此可以利用有序数对来准确的表示物体的位置。此时一般用表示物体的横向位置,用来表示物体的纵向位置。如电影票的号码是第8排第6号,我们可以根据一对整数(8,6)便很快找到座位等。
点击二:点的坐标:
(1)点的坐标:平面内的任意一点都可以用一个有序数对来表示,这个有序数对就叫做这个点的坐标。如图1点A
可以用有序数对(3,4)表示,3叫做
点A的横坐标,4叫做点A的纵坐标,
有序数对(3,4)叫做点A的坐标。
反过来,每一个有序数对对应着平面内的
一个点,如有序数对(-3,-4)表示点B。
(2)由点求其坐标、由坐标定点的方法:
由点求其坐标是:由此点向作垂线,
根据垂足的坐标来确定各点的横坐标和纵坐标。
由坐标定点是:先在上找到表示横坐标的点,再在上找到表示纵坐标的点,过这两个点分别作的垂线,则垂线的交点就是所要画的点。
点击三:平面直角坐标系的组成:
平面直角坐标系是由两条互相垂直且有公共原点的数轴组成。平面直角坐标系将平面分成了以下六个部分:、两坐标轴正方向所夹的部分称为第一象限,从第一象限开始沿逆时针方向分别为:第一象限、第二象限、第三象限、第四象限。六个部分除了有一公共的交点(原点)以外,其他区域之间均没有公共点。
点击四:坐标平面内点的特征:
1.各象限内点的坐标的符号特征:
第一象限(+,+); 第二象限(-,+); 第三象限(-,-); 第四象限(+,-);
2.坐标轴上点的坐标的特征:
的正半轴(+,0);的负半轴(-,0);的正半轴(0,+);的负半轴(0,-)。
3.坐标原点O的坐标为(0,0)。
针对练习1:
1.已知坐标平面内点A(m、n)在第四象限,那么点B(n、m)在()
A,第一象限 B,第二象限 C,第三象限 D,第四象限
2.已知点M(1-a,a +2)在第二象限,则a的取值范围是()
A,a>-2 B,-2<a<1 C,a<-2 D,a>1
3.点P(m +3,m +1)在直角坐标系的x轴上,则P点坐标为()
A,(0,-2) B,(2,0) C,(0,2) D,(0,-4)
4.若0<m<2,则点P(m-2,m)在()
A,第一象限 B,第二象限 C,第三象限 D,第四象限
5.在直角坐标系xOy中,已知A(2,-2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有()
A,2个 B,3个 C,4个 D,5个
6.如果代数式有意义,那么,直角坐标系中点P(m,n)的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在直角坐标系中,A(1,2)点的横坐标乘以-1,纵坐标不变,得到A’点,则A与A’的关系是( )
A.关于x轴对称; B.关于y轴对称;
C.关于原点对称; D.将A点向x轴负方向平移一个单位
8.如图6所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点 ( )
A,(-1,1) B,(-1,2) C,(-2,1) D,(-2,2)
9.若A(a,6),B(2,a),C(0,2)三点在同一条直线上,则a的值为( )
A,4或-2 B,4或-1 C,-4或1 D,-4或2
10.点P(m,1)在第二象限内,则点Q(-m,0)在( )
A,x轴正半轴上 B,x轴负半轴上 C,y轴正半轴上 D,y轴负半轴上
11.点A(,)在第三象限,则的取值范围是( )
A. B. C. D.
答案:1,B;2,D;3,B;4,B;5,C; 6,C;7,B;8,C;9,A;10,A;11,C.
类型之一:体现新课标理念的规律探究型题
例1:一个质点在第一象限及轴、轴上运动,在第一秒钟,它从原点运动到,然后接着按图1中箭头所示方向运动[即 ( http: / / www.21cnjy.com / )],且每秒移动一个单位,那么第35秒时质点所在位置的坐标是( )
A. B. C. D.
解析:这是一道以平面直角坐标系点的坐标为载体的规律探究型问题. 根据条件“按图中箭头所示方向运动,且每秒移动一个单位”我们来看质点从内到外移动到每一个长方形的端点时的时间与坐标变化规律:
第3秒时质点所在位置的坐标是(1,0);
第8(3+5=8)秒时质点所在位置的坐标是(0,2);
第15(8+7=15)秒时质点所在位置的坐标是(3,0);
第24(15+9=24)秒时质点所在位置的坐标是(0,4);
第35(24+11=35)秒时质点所在位置的坐标是(5,0)
解答:选B.
评注:此题若是根据条件硬推则也能得到答案,但就方法显得拙笨.但我们这里根据规律还可知道:第48(35+13=48)秒时质点所在位置的坐标是(0,6);第63(48+15=63)秒时质点所在位置的坐标是(7,0)等.
练习:如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第个点的坐标为____________.(答案:(14,8))
类型之二:考查接受新问题能力的新定义概念题
例2:如图3,在平面内,两条直线,相交于点,对于平面内任意一点,若分别是点到直线,的距离,则称为点的“距离坐标”.根据上述规定,“距离坐标”是的点共有 个.
解析:本题情景新颖,考查学生阅读获取新知识、解决问题的能力,同时还考查了学生遇到新问题时是否善于利用从特殊到一般获取解题的思路.因此本题可以有以下不同层次的三种解法.
解法1:由于“距离坐标”不涉及符号,所以可将新问题转化为平面上一点到两条相交直线的距离问题,逐一画出满足条件的点,从而求解,即是“距离坐标”是的点共有4个.
解法2:将新问题类比为坐标系中点的坐标问题,并注意其差异,利用画平行线的方法,如图4所示,从而得解.即是 “距离坐标”是的点共有、、、4个.
解法3:将一般问题特殊化,将直线、画成两条互相垂直的直线,使问题简单化,如图5所示.所以“距离坐标”是的点共有、、、4个.
( http: / / www.21cnjy.com / )
图4 图5
点评:考查学生获取新知识的能力通常有:(1)定义新概念,考查学生获得新知识并能及时应用的能力,如本例.(2)类比旧知识解决新问题,考查学生的转化能力或者迁移能力.
练习:如图6是中国象棋的一盘残局,如果用表示红“帅”的位置,用表示黑“将”的位置,那么黑“炮”的位置应表示为( )
A. B. C. D.
(答案:A)
类型之三: 在平面直角坐标系中确定点的位置:
例3:已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),I(3,-2),J(2,0),K((3,2),L(1,1).
(1)请在如图所示的平面直角坐标系中,分别描出上述各点,并顺次连结;
(2)试求(1)中连线围成图形的面积.
解析:第(1)小题,依据点的横、纵坐标的定义,分别描出各点并依次连结;第(2)小题,图形被坐标轴平均分成四部分,故只要查出一个象限中图形围起的小正方形的个数,就可求得答案.
解:(1)如右图所示,
(2)∵第一象限中图形围起的小正方形个数为(4-2×-2×)+(3-2×)=4,∴第一象限中图形围起的小正方形的总面积为12×4=4.
∵图形被坐标轴平均分成四部分,∴图形的总面积为4×4=16.
点拨:结合点的坐标与图形中线段长度的意义,合理分割图形、找准小正方形的个数是解答第(2)小题的关键.
类型之四:根据条件判断点所属象限:
例4:已知(a-2)2+(b+3)2=0,试判断点M(-a,-)所在的象限.
分析:由(a-2)2+(b+3)2=0,得a=2,b=-3,所以点M(-2,-)在第三象限.
解:由(a-2)2+(b+3)2=0,得a=2,b=-3,∴-a=-2,-=-,即点M的坐标为(-2,-),又∵-2<0,-<0,∴点M(-a,-)在第三象限.
类型之五:平移在平面直角坐标系中的应用:
例5:如图,三角形A1B1C1是由三角形ABC平移后得到的,三角形ABC中任意一点M(x0,y0)经平移后对应点为M1(x0-5,y0-3),求A1、B1、C1、的坐标,并求出三角形A1B1C1的面积.
分析:观察两个三角形的平移过程,由M(x0,y0)和M1(x0-5,y0-3)可知:三角形A1B1C1是由三角形ABC先向下平移3个单位长度,再左平移5个单位长度,即可求出A1、B1、C1、的坐标,而三角形A1B1C1的面积可以看做是一个长方形的面积减去一些小三角形的面积.
解:由M(x0,y0)和M1(x0-5,y0-3)可知:三角形A1B1C1是由三角形ABC先向下平移3个单位长度,再左平移5个单位长度,相应地,三角形A1B1C1的各个顶点坐标,也是由三角形ABC各个顶点坐标先向下平移3个单位长度,再向左平移5个单位长度,即三角形A1B1C1的各个顶点坐标分别为:A1(-2,3)、B1(-4,-1)、C1(1,1).从三角形A1B1C1的各个顶点构造一个长方形B1DEF,则三角形A1B1C1的面积=长方形B1DEF-三角形A1B1D的面积-三角形A1C1E的面积-三角形B1C1F的面积=5×4-×2×4-×2×3-×2×5=8.
点拨:用坐标表示平移:①平移规律:
②一个图形进行平移,这个图形上所有的点的坐标都要发生相应的变化;反过来,如果图形上的点的坐标发生变化,那么这个图形进行了平移;③平移特征:一个图形平移前后大小、形状完全相同,只是位置不同.同时,还要知道:在坐标系中求一个图形的面积,一般要把它转化为一些能用面积公式表达的图形的和与差来求解,如在本题中所求的三角形面积可以看做一个长方形的面积减去一些小三角形的面积来求解.
1、 填空题
1、 在坐标平面内点的位置与有序实数对是 对应。
2、 点P(a,b)在y轴的正半轴上,则a b
3、 已知点P在第三象限,且到x轴的距离是2,到y轴的距离是3,则点P的坐标为 。
4、 按下列条件确定点为P(x,y)的位置:(1)xy=0,则点P一定在 (2)若x2十y2=0,则点P在
5、 若M点的坐标是(a,一3)N点的坐标(2,b)且点M与点N关于x轴对称则a= b=
6、 已知点A在x轴上,且点A到原点的距离为4个单位,则点A的坐标是
二选择题
1、点P(一3,4)关于y轴对称点的坐标是( )
A(3,一4 ) B(一3,一4) C(3,4) D(一4,一3)
2、点B与点C的横坐标相同,纵坐标不同,则直线BC与x轴的关系为( )
A平行 B垂直 C斜交 D以上都不正确
3、A,B是同一坐标轴上的两个点,A点坐标是(一2,0)A与B的距离是5,则B点的坐标为( )
A(3,0) B(一7,0)
C(3,0)或(一7,0) D(一3,0)或(7,0)
4、以边长为4的正方形的对角线建立直角坐标系,其中一个顶点位于y轴的负半轴上,则该点坐标为( )
A(2,0) B(0,一2)
C(0,2) D(0,一2 )
5、己知M(a,b)在坐标轴上,则a,b满足( )
A、 a=0, B、b=0, C、a=0且b=0, D、ab=0
6、直角坐标系中,点P(x,y)在第三象限,且P到x轴,y轴距离分别为3,7。则P点的坐标为()
A(一3,一7),B(一7,一3),C(3,7)D(7,3)
7、已知A、B两点的连线平行于x轴,y轴,则A、B的坐标之间的关系是( )
A横坐标相同 B纵坐标相同 C横坐标的绝对值相同 D纵坐标的绝对值相同
8、如果P(m十3,2m十4)在y轴上,那么点P的坐标( )
A(一2,0)B(0,一2)C(1,0)D(0,1)
三、解答题
1、 如图为画在方格纸上的花坛设计简图,
(1) 请写出图中平行四边形ABCD各个顶点的坐标。在图中A与D,B与C的纵坐标相同吗?为什幺?
(2) A与B,C与D的横坐标相同吗?为什么?
2、如图三角形AOB中,A,B两点的坐标分别为(2,4)(6,2)求三角形AOB的面积。
3、 己知矩形ABCD中AB=4,BC=6这AB//x轴,若点A的坐标为(一1,2)求C点的坐标。
4、如图菱形ABCD的中心在直角坐标系的原点,一条边AD与x轴平行,己知点A,D的坐标分别是(一4,3)(,3)求B、C的坐标。
(提示:A、C;B,D关于原点对称)
5.下面是某小区的公共设施图,请你建立适当的直角坐标系,写出各处的坐标。
6.如图△ABC与△关于y轴对称,根据图形的位置写出△ABC与△各顶点的坐标
思考:关于y轴对称的两个图形的对应顶点的坐标有什么关系?
参考答案
一、1、一一对应
2、=0,>0
3、(-3,-2)
4、x轴或y轴包括原点,原点
5、2,3
6、(4,0)或(-4,0)
二、1、C2、B3、B4、C5、D6、A7、B8、B
三、1、(1)A(-3,4)B(-6,-3)C(4,-3)D(7,4)A与D,B与C的纵坐标相同(2)不相同因为不平行于y轴
2、10
3、(3,8)(-5,8)
4、B()C(4,一3)
5、略
6、A(0.5,0)B(3,2)C(2,4)A’(一0.5,0)B’(一3,2)C’(一2,4)关于y轴的两个图形的顶点的横坐标互为相反数,纵坐标不变。
一.选择题
1.如图1所示,一方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B 的位置是 ( )毛
A. (4, 5); B.(5,4); C.(4,2); D.(4,3)
2.如图1所示,B左侧第二个人的位置是 ( )
A.(2,5); B.(5,2); C.(2,2); D.(5,5)
3.如图1所示,如果队伍向西前进,那么A北侧第二个人的位置是 ( )
A.(4,1); B.(1,4); C.(1,3); D.(3,1)
4.如图1所示,(4,3)表示的位置是 ( )
A.A B.B C.C D.D
5.如图2所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
6.如图2所示,横坐标和纵坐标都是负数的点是 ( ) A.A点 B.B点 C.C点 D.D点
7.如图2所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
8.若点M的坐标是(a, b),且a>0,b<0,则点M在( )
A.第一象限;B.第二象限; C.第三象限;D.第四象限
二.填空题
1.如图2所示,进行“找宝”游戏,如果宝藏藏在(3,3)字母牌的下面, 那么应该在字母______的下面寻找.
2.如图3所示,如果点A的位置为(3,2),那么点B的位置为______, 点C 的位置为______,点D和点E的位置分别为______,_______.
3.如图4所示,如果点A的位置为(1,2),那么点B的位置为_______,点C 的位置为_______.
4.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
5.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
6.在坐标平面内,已知点A(a, b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
7.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
8.已知点M(a, b),当a>0,b>0时,M在第_______象限;当a____, b______时,M 在第二象限;当a_____, b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
三.
1.如图所示,A的位置为(2,6),小明从A出发,经
(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经
(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
2. 如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法
3. 如图所示,四个正方形组成一个“T”字形,你能用四个这样的图形拼成一个正方形吗
4. 如果点A的坐标为(a2+1,-1-b2),那么点A在第几象限 为什么
5. 如果点A(t-3s,2t+2s),B(14-2t+s,3t+2s-2)关于x轴对称,求s, t的值.
6. 如图所示,C,D两点的横坐标分别为2,3,线段CD=1;B,D两点的横坐标分别为-2,3,线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1
8. 如图4所示,图中的能走遍棋盘中的任何一个位置吗 若不能,指出哪些位置无法走到;若能,请说明原因.
答案:
一.1.A 2.A 3.B 4.C 5.B 6.C 7.D 8.D
二.1.M 2.(0,1) (1,3) (2,5) (2,1) 3.(0,1) (-1,0)4.(-1,2) (-1,-2) (1,-2) 5. (4,6) (-4,-6)
6.(a,-b) (-a,b) 7. 二 四 一 三 y x 8.一 <0 >0 >0 <0 三
三.1.3个格. 2. 解:如图所示的是最短路线的6种走法.
3. 解:如图所示.毛
4. 解:∵a2+1>0,-1-b2<0,
∴点A在第四象限.
5. 解:∵关于x轴对称的两个点的横坐标相等,纵坐标互为相反数,
∴
即,两式相加得8t=16,t=2.
3×2-4s=14,s=-2.
6. 解:(1)MN=x2-x1 (2)PQ=y2-y1
7. 解:根据题意可得3x-13y+16=0,x+3y-2=0,
由第2个方程可得x=2-3y,
∴第1个方程化为3(2-3y)-13y+16=0,
解得y=1,x=2-3y=-1,
∴点P(x,y),即P(-1,1) 在第二象限,Q(x+1,y-1),
即Q(0,0)在原点上.
8. 提示: 能走遍棋盘中的任何一个位置,
只需说明 能走到相邻的一个格点即可.毛
1.如图7,把矩形OABC放置在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF.
(1)可以通过________办法,使四边形AEFO变到四边形BEFC的位置(填“平移”、“旋转”或“翻转”);
(2)求点E的坐标;
(3)若直线l把矩形OABC的面积分成相等的两部分,则直线l必经过点的坐标是_____.
2.如图8,在平面直角坐标系中,已知点为A(-2,0),B(2,0).
(1)画出等腰三角形ABC(画出一个即可);
(2)写出(1)中画出的ABC的顶点C的坐标.
3.如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.如图9,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…….对称中心分别是A、B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标.
答案:1.(1)旋转,(2)(6,),(3)(3,4);2.略;3.P2(1,-1) ,P7(1,1) ,P100(1,-3).
课时作业:
A等级
一、填空题
1、若点P(10一2a,3一b)的横坐标是正数,纵坐标是负数,则a b
2、巳知,则点(x,y)在 象限。
3、若Rt△ABC的各顶点坐标分别是A(0,一4),B(3,0)C(0,0)则△ABC的各边长是AC= BC= AB= △ ABC的面积
4、将△ABC绕坐标原点旋转后,各顶点坐标变化特征是
二.选择题
1、到x轴的距离是3且到y轴的距离是4的点有( )
A1个 B2个 C3个 D4个
2、 菱形ABCD的两条对角线分别是8和6,以对角线AC,BD的交点O为坐标原点,AC所在直线为横轴,建立直角坐标系,则A点的坐标可能是( )
A(0,一4)B(0,一3)C(0,4)D(一4,0)
3、己知A、B两点的连线平行于x轴,则A、B的坐标之间的关系是()
A、 横坐标相同B、纵坐标相同C、横坐标的绝对值相同D、纵坐标的绝对值相同
三、解答题
1、 若有序数对(3,a)(b,5)所在的两点连线与水平方向垂直且两点不重合,则a,b应满足的条件?
2、 假设我们约定“列数在前,排数在后”那么下列五位学生的座位自前至后的排列是
A(5,9)B(3,2)C(4,3)D(2,8)E(1,6)若“排数在前,列数在后”呢?
3、 在直角坐标系内,将坐标为(1,1)(2,1)(2,2)(1,2)(1,3)(2,3)的点依次连结起来,组成一个图形。
(1) 横坐标,纵坐标分别乘以一1呢?
(2) 横坐标不变,纵坐标乘以一1呢?
4、 在直角坐标系中描出下列各点,并将各组内的点用线段依次连接起来。
a、(5,1)(5,3)(1,3)(1,7)(5,7)(5,8)(7,8)(7,7)(11,7)(11,3)(7,3)(7,1)(5,1)
b、(5,4)(3,4)(3,6)(5,6)(5,4)
c、(7,4)(7,6)(9,6)(9,4)(7,4)
(1) 观察所得图形,你觉得他象什么?
(2) 纵坐标保持不变,横坐标分别乘以一1,所得图案与原来的图案相比有什么变化?
B等级
1. 已知点,是轴上的点,则.
2. 已知直线平行于轴,且点坐标为,,则点坐标为 ,条件 .
3. 若点,在第一、三象限角平分线上,求的值.
4. 已知两点,,,,若轴,求的值,并确定.
5. 已知点坐标为,,且点到两坐标轴距离相等,求点坐标.
6. 如图,点的坐标是 ,点的坐标是 ,点的坐标是 ,坐标是的点是 ,坐标是的点是 ,点的坐标是对吗? .(填“对”“不对”,并填出正确答案)
7 写出图中所标出的各点的坐标.
8. 已知点在第二象限,它的横坐标与纵坐标的和为1,则点的坐标是 (写出符合条件的一个点即可).
9. 如图,是某市几个单位的示意图(图中每个小正方形的边长为1个单位长度),请以某一个单位为原点,画出平面直角坐标系,并写几个单位的坐标.
10. 若点,在第四象限,则,.
11. 若点的横坐标是-3,纵坐标是2,则点的坐标记作 ,点在第 象限.
12. 若点,在第二象限,则点,在第 象限.
13. 若点,是第二象限内的点,则必须满足 .
14. 若点,在第二象限,,在第三象限,则点,在第 象限.
15. 下列各点:,,,,,,,,,,,中,位于第一象限的有 ,位于第三象限的有 ,位于坐标轴上的有 .
16. 设点的坐标为,,根据下列条件,判定点在坐标平面内位置:
⑴;⑵;⑶.
17. 如果点,在第一象限,那么点,在 ( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
18. 已知点,,下列说法正确的有 ( )
A.当时,点在轴上 B.当时,点在轴上
C.当时,点在第一或第四象限 D.当时,点在轴左方
19. 按下列条件确定点,的位置:
⑴,,则点在 .
⑵,则点一定在 .
⑶若,则点在 .
20. 如果点,在第二象限,那么点,在第 象限.
21. 已知点,在轴的负半轴上,则点,在( )
A.第一象限 B.第二象限 C.第三角限 D.第四象限
22. 已知点,,且,则点在 ( )
A.原点 B.轴上 C.轴上 D.坐标轴上
23. 平行于轴的一条直线上的点的横坐标一定 ( )
A.大于0 B.小于0 C.相等 D.相反
24. 已知点,关于轴的对称点是 ,关于轴的对称点是 ,关于原点的对称点是 .
25. 点,关于轴的对称点的坐标是 ( )
A., B., C., D.,
26. 已知点,,,,如果,,那么点,( )
A.关于原点对称 B.关于轴对称
C.关于轴对称 D.关于过点(0,0),(1,1)的直线对称
C等级
1. 在坐标平面内点的位置与有序实数对 对应.
2. 如图所示的马所处的位置为(2,3).
⑴你能表示图中象的位置吗?
⑵写出马的下一步可以到达的位置.
3. 有序数对的意义是 ,利用有序数对,可以很准确地 .
4. 如果约定街在前,巷在后,则某单位在5街2巷的十字路口,用有序数对表示为( )
A.(2,5) B.(5,2) C.(5,5) D.(2,2)
5. 如图,写出表示下列各点的有序数对:
(_,_);(5,2);(_,_);(_,_);(_,_);(_,_);(_,_);(_,_);(_,_);
6. 如图,表示下列图形格点的有序数对.
(1,4)( )( )( )( )( )( )
7. 有序数对(2,3)和(3,2)相同吗?如果有序数对,表示某栋楼房中层楼号房,那么有序数对(2,3)和(3,2)分别代表什么?
8. 如图,甲处表示三街与二巷的十字路口,乙处表示六街与六巷的十字路口,如果用(3,2)表示甲处位置,那么(3,2)→(3,3)→(3,4)→(3,5)→(3,6)→(4,6)→(5,6)→(6,6)表示从甲处到乙处的一条路线,请你用有序数对写出其他几种从甲处到乙处的路线.
9 为了用一对实数表示平面内的点,在平面内画两条互相垂直的数轴,组成了 ,水平的数轴叫做 ,取 为正方向,铅直的数轴叫做 ,取 为正方向.
10. 画平面直角坐标系,标出下列各点:
点在轴上,位于原点上方,距离原点2个单位长度;
点在轴上,位于原点右侧,距离原点1个单位长度;
点在轴上方,轴右侧,距离每条坐标轴都是2个单位长度;
点在轴上,位于原点右侧,距离原点3个单位长度;
点在轴上方,轴右侧,距离轴2个单位长度,距离轴4个单位长度,依次连接这些点,你能得到什么图形?
11. 如图,正方形的边长为2,建立适当的平面直角坐标系,分别表示,,,四个点的坐标.
12. 如图是画在方格纸上的某一小岛的示意图.
⑴分别写出地点,,,,的坐标;
⑵(3,6),(7,9),(8,7),(3,3)所代表的地点分别是什么?
13. 在如图所示的坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
⑴(1,2),(2,1),(6,1),(7,3);
⑵(3,3),(3,6),(5,2.5);
观察所得到的图形,你觉得它像什么?
14. 点的坐标是,则是点的 ,是点的 ,点在第 象限.
15. 已知点到轴、轴的距离分别为2和,若点的横坐标、纵坐标都是正值,则点坐标是 .
16. 点位于轴左方,距轴3个单位长,位于轴上方,距轴四个单位长,点的坐标是 ( )
A. B. C. D.
17. 在直角坐标系中,点,在第二象限,且到轴、轴距离分别为3,7,则点坐标为( )
A. B. C. D.
18. 已知点(1,2),轴于,则点坐标为 ( )
A.(2,0) B.(1,0) C.(0,2) D.(0,1)
19. 已知点,满足,则点的位置是 ( )
A.在轴或轴上
B.在第一、三象限坐标轴夹角平分线上
C.在第二、四象限坐标轴夹角平分线上
D.在坐标轴夹角平分线上
20. 正方形中,,,坐标分别是,,,则顶点坐标是 .
21. 自画一个坐标系并描出下列各点:
(2,1),(-2,1),(4,-3),(4,3),(-3,-2),(3,2),(0,-1),(,0).
根据在坐标系中描出的点观察:与,与,与在位置上有何特点?并说明它们纵、横坐标各有什么特点.
22. 如图,在所给的坐标系中描出下列各点的位置:
,,,,,.
你发现这些点有什么关系?你能再找出一些类似的点吗?
23. 在方格纸上建立一个平面直角坐标系,描出点,,连接,若点为直线上的任意一点,则点的纵坐标是什么?
⑴如果一些点在平行于轴的直线上,那么这些点的纵坐标有什么特点?
⑵如果一些点在平行于轴的直线上,那么这些点的横坐标有什么特点?
24. 在下图所示的直角坐标系中描出下列各点:
,;,;,;,;,;,;,;,;,;,;,.
依次连结各点,观察得到的图形,你觉得它像什么?
25. 李强同学家在学校以东100m再往北150m处,张明同学家在学校以西200m再往南50m处,王玲同学家在学校以南150m处,如图,在坐标系中画出这三位同学家的位置,并用坐标表示出来.
26. 根据下图填表.
点 坐标 象限或坐标轴
课时作业答案;
A等级答案:
一1、 <3, >3
2 、 一
3、4,3,5,6 ;
4、横坐标纵坐标均为相反数
二
1 、D 2 、D3、B
三、
1、b=3,
2、BCEDA,EDBCA
3、(1)所得的图形被横向拉长了一倍
(2)所得的图形向y轴正方向平移了3个单位
(3)所得的图形与原图形关于原点对称
(4)所得的图形与原图形关于x轴对称
4、(1)“中”字(2)关于y轴的对称图案。
B等级答案
1:.2:,,.3:.4:,.5:,.
6:;;;点;点;不对..
7:;;;;;;.
8:有无数个.例如:.9:略.10:>,<.11:,二.12:四.13:.
14:三.15:,;;,.
16:⑴坐标轴上;⑵点在第一或第三象限;⑶点在第二或第四象限.
17:C.18:D.19:⑴轴的负半轴上;⑵坐标轴上;⑶原点.20:三.21:B.22:A.
23:C.24:,,.25:A.26:D.
C等级答案
1:一一.2:⑴ 象的位置(5,3);
⑵马的下一步可到达位置(1,1)(3,1)(4,2)(1,5)(3,5).
3:有顺序的两个数与组成的数对记为;表示一个位置.4:B.
5:(3,3);(5,2);(7,3);(10,3);(10,5);(7,7);(5,7);(3,6);(4,8).
6:(1,4);(3,1);(7,1);(9,2);(8,4);(6,3);(4,6).
7:不同.2层楼3号房;3层楼2号房.8:略.9:平面直角坐标系;轴,向右;轴,向上.10:略.11:略.12:⑴(2,9);(5,8);(5,5);(7,4);(8,1);⑵分别代表点:,,,.13:略.14:横坐标,纵坐标,三.15:(,2).16:B.17:B.18:B.19:D.20:.21:略.
22:这些点都在过原点经过一、三象限的一条直线上,且这条直线上的任意一个点到轴、轴距离相等.能找很多:(1,1),(0.2,0.2).
23:点纵坐标为4.⑴都相等;⑵都相等24:像五角星.25:李强家;张明家;王玲家.26:略.
A
B
C
O
E
F
x
y
图7
图6
O
(1,0)
(2,0)
(3,0)
(4,0)
(5,0)
x
(5,1)
(4,1)
(3,1)
(2,1)
(3,2)
(4,2)
(4,3)
(5,4)
(5,3)
(5,2)
y
图2
0
1
2
3
x
y
1
2
3
…
图1
图3
将
士
炮
卒
仕
帅
兵
兵
(图6)
A′(x+a,y)或(x-a,y)
B′(x,y+b)或(x,y-b)
向右或向左平移
a个单位
向上或向下平移
b个单位
点A(x,y)
A
B
C
O
E
F
x
y
图7
图8
图9
体育馆
广场
学校
商场
幼儿园
1
2
3
4
5
2
3
4
5
6
7
8
9
象
马
0
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
10
一巷
二巷
三巷
四巷
五巷
六巷
七巷
一街
二街
三街
四街
五街
六街
七街
八街
甲
乙
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
1
2
3
1
2
3
北
东
单位:m
0
50
50
1
2
3
4
5
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
