第3课时 二元一次方程组的应用
文档属性
| 名称 | 第3课时 二元一次方程组的应用 |  | |
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-17 18:06:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第八章 二元一次方程组
第10课时 二元一次方程组的应用
对于二元一次方程组的应用问题,关键是由实际问题向数学问题的转化过程。所以在教学过程中注重分析问题的方法,让学生学会用数学建模的思想和方程的思想来解决问题。例题的选取也是从实际出发,让学生初步体会到数学与人们的日常生活的密切关系,并体会数学在社会生活中所起的作用,激发学生对数学的学习兴趣,使学生学会从数学的角度去分析和解决简单的实际问题。
二元一次方程组的应用,是在学习了二元一次方程组解法的基础上进行的,在生活实践和数学领域里有着非常广泛的应用。重点是列二元一次方程组解决实际问题.难点是在实际问题中找等量关系、列方程组.
点击一:列二元一次方程组解应用题的一般步骤可概括为“审、找、列、解、答”五步,即:
(1)审:通过审题,把实际问题抽象成数学问题,分析已知数和未知数,并用字母表示其中的两个未知数;
(2)找:找出能够表示题意两个相等关系;
(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;
(4)解:解这个方程组,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案.
针对练习:
1.某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,问中、小型汽车各有多少辆?
2.某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 直接销售 粗加工后销售 精加工后销售
每吨获利(元) 100 250 450
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行).
(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 全部直接销售 全部粗加工后销售 尽量精加工,剩余部分直接销售
获利(元)
(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?
3.为满足市民对优质教育的需求,某中学决定改变办学条件,计划拆除一部分旧校舍,建造新校舍,拆除旧校舍每平方米需80元,建新校舍每平方米需700元. 计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿地面积,新建校舍只完成了计划的80%,而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.
(1)求:原计划拆、建面积各是多少平方米?
(2)若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?
答案:1.解:设中型汽车有x辆,小型汽车有y辆.由题意,得
解得,
故中型汽车有15辆,小型汽车有35辆.
2.解:(1)全部直接销售获利为:100×140=14000(元);
全部粗加工后销售获利为:250×140=35000(元);
尽量精加工,剩余部分直接销售获利为:450×(6×18)+100×(140-6×18)=51800(元).
(2)设应安排x天进行精加工, y天进行粗加工.
由题意,得
3.(1)原计划拆、建面积各是4800平方米、2400平方米;
(2)可绿化面积为1488平方米.
解得,
故应安排10天进行精加工,5天进行粗加工.
类型之一:图形信息题
例1.扬子江药业集团生产的某种药品包装盒的侧面展开图如图所示.如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.
解析:要求包装盒的体积,必须先求出这种包装盒的长、宽、高,由于长方体盒子的长比宽多4cm,因此可设宽为,高为后列二元一次方程组求解.
解:设这种药品包装盒的宽为,高为,则长为,
根据题意得,
解这个方程组得
故长为9cm,宽为5cm,高为2cm.
体积
答:这种药品包装盒的体积为.
类型之二:图画信息题
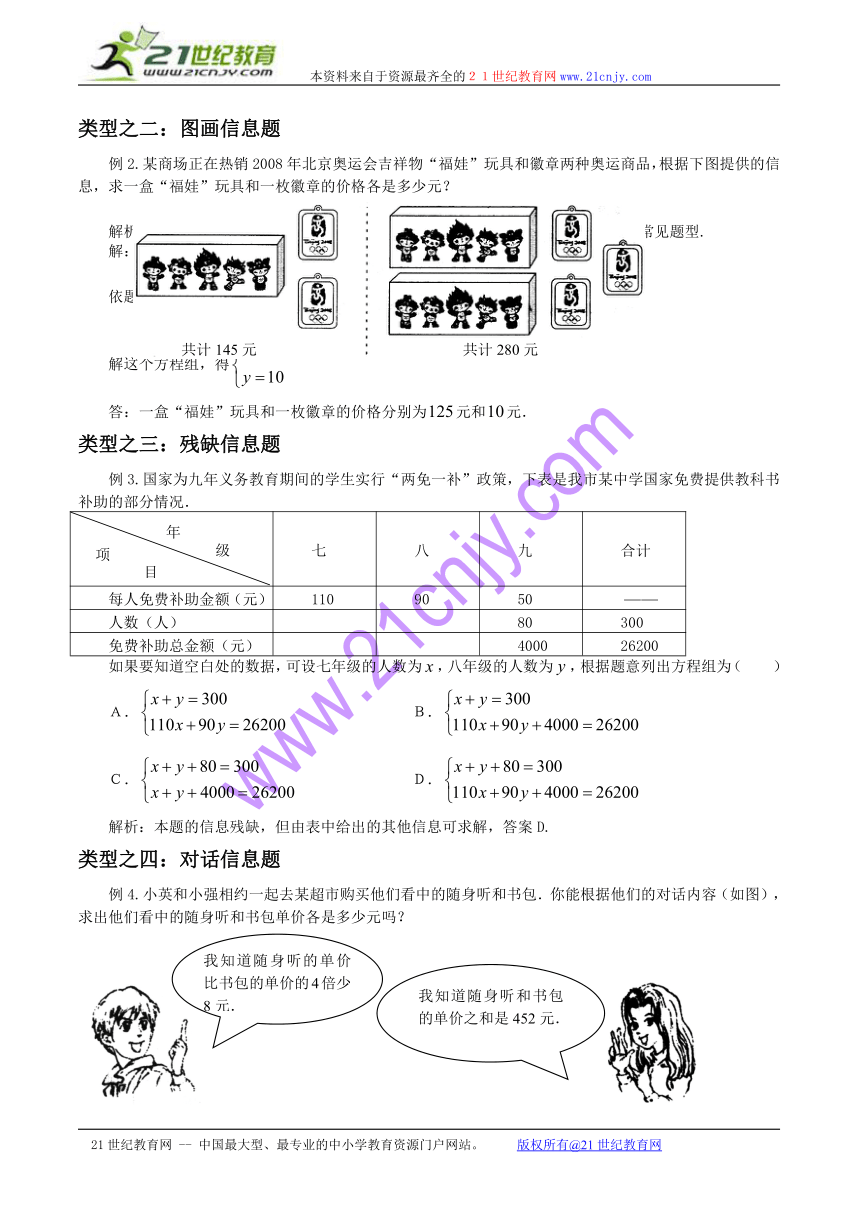
例2.某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少元?
解析:本题的条件由图画给出,形式新颖,这也是近几年二元一次方程组应用的常见题型.
解:设一盒“福娃”玩具和一枚徽章的价格分别为元和元.
依题意,得
解这个方程组,得
答:一盒“福娃”玩具和一枚徽章的价格分别为元和元.
类型之三:残缺信息题
例3.国家为九年义务教育期间的学生实行“两免一补”政策,下表是我市某中学国家免费提供教科书补助的部分情况.
七 八 九 合计
每人免费补助金额(元) 110 90 50
人数(人) 80 300
免费补助总金额(元) 4000 26200
如果要知道空白处的数据,可设七年级的人数为,八年级的人数为,根据题意列出方程组为( )
A. B.
C. D.
解析:本题的信息残缺,但由表中给出的其他信息可求解,答案D.
类型之四:对话信息题
例4.小英和小强相约一起去某超市购买他们看中的随身听和书包.你能根据他们的对话内容(如图),求出他们看中的随身听和书包单价各是多少元吗?
解:设他们看中的书包的单价为元,随身听的单价为元.
依题意有
解得
答:(略)
类型之五:表格信息型
例5 某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 西红柿 豆角
批发价(单位:元/㎏) 1.2 1.6
零售价(单位:元/㎏) 1.8 2.5
问:他当天卖完这些西红柿和豆角能赚多少钱?
(无锡市中考题)
解析:由表中提供的数据可知每斤西红柿批发价1.2元/㎏,零售价1.8元/㎏,净赚0.6元/㎏;每斤豆角批发价1.6元/㎏,零售价2.5元/㎏,净赚0.9元/㎏。利用上述信息找出等量关系列方程组求解。
解:设批发西红柿xkg,批发豆角ykg,则卖完净赚(0.6x+0.9y)元,根据题意得
解得
∴0.6x+0.9y=0.6×10+0.9×30=33(元)
答:他当天卖完这些西红柿和豆角能赚33元钱。
类型之六:情景对话型
例6 在当地农业技术部门指导下,小明家增加种植菠萝的投资,使今年的菠萝喜获丰收。下面是小明爸爸、妈妈的一段对话。
请你用学过的知识帮助小明算出他们家今年菠萝的收入。(收入-投资=净赚)
(海南省中考题)
解:设小明家去年种植菠萝的收入为x元,投资为y元,根据题意得
解得
∴小明家今年菠萝的收入应为:
(1+35%)x=1.35×12000=16200元
类型之七:解答说理型
例7 随着我国人口增长速度的减慢,小学入学儿童数量每年按逐渐减少的趋势发展。某区2003年和2004年小学儿童人数之比为8:7,且2003年入学人数的2倍比2004年入学人数的3倍少1500人。某人估计2005年入学儿童数将超过2300人。请你通过计算,判断他的估计是否符合当前的变化趋势。
(吉林省中考题)
解:设2003年入学儿童人数为x人,2004年入学儿童人数y人,根据题意得
解得
∵2300>2100
∴他估计不符合当前入学儿童逐渐减少的趋势。
类型之八:几何拼图型
例8 如图1,图2,是由8个一样大小的小长方形拼成的,且图2中的小正方形(阴影部分)的面积为1cm2,求小长方形的长和宽。
(大连市中考题)
解析:小正方形面积为1cm2,则意味着它的边长为1cm,若再注意到矩形的长或宽的构成方式,则不难求出。本例着重考察学生的数形结合思想及方程建模能力。
解:设小长形的长为xcm,宽为ycm,根据题意,得
解得
答:小长形的长为5cm,宽为3cm。
类型之九:药品降价问题
例9:2001年以来,我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如表二所示,表中缺失了2003年、2007年相关数据.已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额.
年份 2001 2003 2004 2005 2007
降价金额(亿元) 54 35 40
表二
解析 要求2003年和2007年的药品降价金额.设2003年和2007年的药品降价金额分别为亿元、亿元,由表中提供的信息即可根据题意即可列出二元一次方程组求解.
解:设2003年和2007年的药品降价金额分别为亿元、亿元.
根据题意, ( http: / / www.21cnjy.com / )
解方程组,得 ( http: / / www.21cnjy.com / )
答:2003年和2007年的药品降价金额分别为20亿元和120亿元.
点评:当一个问题直接求解有困难时,不妨换一种思维,间接求解.本题中通过先分别求出红辣椒和西红柿的重量即可使问题获解.
类型之十:团体购票问题
例10:团体购买公园门票票价如下:
购票人数 1~50 51~100 100人以上
每人门票(元) 13元 11元 9元
今有甲、乙两个旅行团,已知甲团人数少于50人,乙团人数不超过100人.
若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计
应付门票费1080元.
(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
解析:本题以表格形式提供了部分信息,主要考查运用二元一次方程组解决实际问题的能力.
分析 由题意我们可得到列方程组的关系,这样就可列方程组求解.
解:(1)∵100×13=1300<1392
∴乙团的人数不少于50人,不超过100人
(2)设甲、乙两旅行团分别有x人、y人,
则 ( http: / / www.21cnjy.com / )
解得:
所以甲、乙两旅行团分别有36人、84人
点评:本题是一道列二元一次方程组的应用题,要注意结果是否是原方程组的解,解是否符合实际意义.
类型之十一:决策型问题
例11.某公司现有甲、乙两种品牌的计算器,甲品牌计算器有三种不同的型号,乙品牌计算器有两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
(1)写出所有的选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么型号计算器被选中的概率是多少?
(3)现知新华中学购买甲、乙两种品牌计算器共40个(价格如图所示),恰好用了1000元人民币,其中甲品牌计算器为型号计算器,求购买的型号计算器有多少个?
解:(1)树状图表示如下:
甲
列表表示如下:
有6种可能结果:.
说明:用其它方式表达选购方案且正确者,只给1分.
(2)因为选中型号计算器有2种方案,即,所以型号计算器被选中的概率是.
(3)由(2)可知,当选用方案时,设购买型号,型号计算器分别为个,
根据题意,得解得
经检验不符合题意,舍去;
当选用方案时,设购买型号、型号计算器分别为个,
根据题意,得解得
所以新华中学购买了5个型号计算器.
【点评】解这类问题,要求要读懂题意,获得正确的信息.是把实际决策问题转化为二元一次方程组来解决.即通过构建数学模型解决实际应用题,这是中考的热点问题
类型之十二:配套问题
例12:现有190张铁皮,每张铁皮可做8个盒身或做22个盒底,一个盒身与两个盒底配成一个完整盒子,那么用多少张铁皮制盒身,多少张铁皮制盒底,可以正好制成一批完整的盒子
解析:此题有两个未知量——制盒身、盒底的铁皮张数.
问题中有两个等量关系:⑴制盒身铁皮张数+制盒底铁皮张数=190;
⑵制成盒身的个数的2倍=制成盒底的个数.
解:设x张铁皮制盒身,y张铁皮制盒底,
根据题意,得
解这个方程组,得
答:110张制盒身,80张制盒底,可以正好制成一批完整的盒子.
一、选择题
1,某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏本20%,在这项买卖中,这家商店( )
A.赔了8元 B.赚了32元 C.不赔不赚 D.赚了8元
2,甲、乙两人相距42km,若相向而行,2小时相遇;若同向而行,乙14小时就能追上甲,则甲、乙二人每小时各走( )
A.12 km、9 km B.11 km、10 km
C.10 km、11 km D.9 km、12 km
3,一个两位数,对换它的十位数字与个位数字后,所得的数是原数的,则这样的两位数的个数有( )
A.0个 B.3个 C.4个 D.无数多个
4,已知 是方程5x-ky=3的一个解,则k-1=( )
A.0 B.1 C.2 D.3
5,为保护生态环境,我省某山区县响 国家“退耕还林”号召,将该县某地一部分耕地改为林地,改变后,林地面积和耕地面积共有180 平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各为多少平方千米,设耕地面积为x平方千米,林地面积为y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
A. B. C. D.
6,用化肥x千克给一块y公顷的麦地施肥,若每公顷用 化肥23千克,则还差90千克;若每公顷用化肥18千克,则还多余110千克,由题意,可列出方程组( )
A. B. C. D.
二、填空题
7,若实数m、n满足条件m+n=3,且m-n=1,则m=_____,n=_______.
8,已知二元一次方程组的解是则a+b的值为______.
9,已知等式(2A-7B)x+(3A-8B)=8x+10对一切实数x都成立,则A=___,B=___.
10,如果3a7xby+7和-7a2-4yb2x是同类项, 则x=_____,y=_____.
11,将若干只鸡放入若干个笼中,若每个笼中放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,则至少有___只鸡.
12,某山区有23名中、小学生因贫困失学需要捐助, 资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表:
初一年级 初二年级
捐款数额(元) 4 000 4 200
捐助贫困中学生人数(名) 2 3
捐助贫困小学生人数(名) 4 3
则a=___,b=___.
13,某校去年有学生1000名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x名,走读学生y名,则可列出方程组为 .
14,以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺,绳长、井深各几何?若设绳长x尺,井深y尺,则可列方程组为 .
三、解答题
15,仔细观察如图2,认真阅读对话:
根据以上对话内容,可知小明买5元邮票是多少张?
16,在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10 000辆”;
乙同学说:“四环路比三环路车流量每小时多2 000辆”;
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”.
请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少.
17,甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
18,有三把楼梯,分别是五步梯、七步梯、九步梯,每攀沿一步阶梯上升的高度是一致的.每把楼梯的扶杆长(即梯长)、顶档宽、底档宽如图3所示,并把横档与扶杆粘合处称作联结点(如点A).
(1)通过计算,补充填写下表:
楼梯种类 两扶杆总长(米) 横档总长(米) 联结点数(个)
五步梯 4 2.0 10
七步梯
九步梯
(2)一把楼梯的成本由材料费和加工费组成,假定加工费以每个个联结点1元计算,而材料费中扶杆的单价与横档的单价不相等(材料损耗及其它因素忽略不计).现已知一把五步梯、七步梯的成本分别是26元、36元,试求出一把九步梯的成本.
19,“利海”通讯器材商场,计划用60 000元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部1 800元,乙种型号手机每部600元 ,丙种型号手机每部1200元.若商场同时购进其中两种不同型号的手机共40部,并将60 000元恰好用完,请你帮助商场计算一下如何购买.
参考答案:
一、1,D;2,D;3,C;4,A;5,B;6,A.
二、7,m=2, n=1;8,把x=2,y=1代入原方程组,得 (1)+(2)得3(a+b)=9,∴a+b=3;9,由于等式(2A-7B)x+(3A-8B)=8x+10对一切实数x都成立,所以根据待定系数即可得到关于A、B的二元一次方程组,即解得10,x=2,y=-3;11,25;12,根据题意,得解这个方程组,得 13,;14,.
三、15,设小明买2元邮票x张,1元邮票2x张,5元邮票y张,则根据题意,得解得即小明买3张5元邮票.
16,设高峰时段三环路的车流量为每小时x辆,四环路的、车流量为每小时y辆.根据题意,得 解这个方程组,得 答:高峰时段三环路的车流量为每小时11 000辆,四环路的车流量为每小时13 000辆;
17,设甲、乙两件服装的成本分别是x元、y元.根据题意,得
解这个方程组,得答 甲、乙两件服装的成本分别是300元、200元.
18,(1)七步梯、九步梯的扶杆长分别是5米、6米;横档总长分别是3.5米、3.5米;联结点个数分别是14个、18个.(2)设扶杆单价为x元/米,横档单价为y元/米.依题意得:即解得故九步梯的成本为6×3+5.4×2+1×18=46.8(元)即一把九步梯的成本为46.8元.
19,设甲种型号手机要购买x部,乙种型号手机要购买y部,丙种型号手机要购买z部,根据题意,得或
或分别解这三个方程组,得 或 或 (不合题意,舍去)答 有两种购买方法:甲种型号手机购买30部,乙种型号手机购买10部;或甲种型号手机购买20部,丙种型号手机购买20部.
一、耐心填一填,一锤定音!(每小题6分,共30分)
1.在方程中,如果是它的一个解,那么的值为______.
2.大数和小数的差为,这两个数的和为,则大数是______,小数是______.
3.买支铅笔和本练习本,共用元.若铅笔每支元,练习本每本元,写出以和为未知数的方程为______.
4.甲、乙两人速度之比是,则他们在相同时间内走过的路程之比是______,他们在走相同路程所需时间之比是______.
5.羊圈里白羊的只数比黑羊的脚数少,黑羊的只数比白羊的脚数少,则白羊有______只,黑羊有______只.
二、精心选一选,慧眼识金!(每小题5分,共15分)
1.既是方程的解,又是方程的解是( )
A. B. C. D.
2.甲、乙两数这和为,甲数的倍等于乙数的倍,若设甲数为,乙数为,则方程组(1)(2)(3)(4)中,正确的有( )
A.组 B.组 C.组 D.组
3.某校名学生参加竞赛,平均分为分,其中及格学生平均分为分,不及格学生平均分为分,则不及格学生的人数为( )
A. B. C. D.
三、用心做一做,马到成功!(本大题共20分)
1.(本题10分)根据下图提供的信息,求每件恤衫和每瓶矿泉水的价格.
2.(本题10分)小明到商店买东西,下面是他和售货员阿姨的对话:“我买这种牙膏支,这种牙刷把”.“一共元角”.付款后,小明说:“阿姨,这支牙膏我不要了,换一把牙刷吧!”“还需找你元”.从他们的对话中你能知道牙刷、牙膏的单价吗?
四、综合运用,再接再厉!(本大题共35分)
1.(本题11分)如图,周长为的长方形被分成个相同的长方形,求长方形的长和宽.
2.(本题12分)长沙市某公园的门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
票价 10元/人 8元/人 5元/人
某校七年级甲、乙两班共多人去该公园举行联欢活动,其中甲班多人,乙班不足人.如果以班为单位分别买票,两个班一共应付元;如果两个班联合起来作为一团体购票,一共只要付元.问:甲、乙两班分别有多少人?
3.(本题12分)有甲、乙、丙三种规格的钢条,已知甲种根,乙种根,丙种根,共长米;甲种根,乙种根,丙种根共长米,问甲根,乙根,丙根共长多少?
参考答案
一、1. 2., 3. 4., 5.,
二、1.B 2.C 3.D
三、1., 2.,
四、1., 2., 3.米
1.某酒店客房部有三人间、双人间客房,收费数据如下表.
普通(元/间/天) 豪华(元/间/天)
三人间 150 300
双人间 140 400
为吸引游客,实行团体入住五折优惠措施.一个50人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房.若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人间和双人普通间客房和多少间?
解:设三人普通房和双人普通房各住了,间,根据题意,得
解得答:略.
聪明的你还能怎样设未知数解答本题呢?
2.根据右图提供的信息,求出每支网球拍的单价为__元,每支乒乓球拍的单价为__元.
解:设每支网球拍元,每支乒乓球拍元,根据题意,得
解得
3.
解:设1本笔记本元,1支钢笔元,根据题意,得
EMBED Equation.3 解得答:略.
4.在“五一”黄金周期间,小明、小亮等同学随家人一同到江郎山游玩.下面是购买门票时,小明与
他爸爸的对话:
问题:(1)小明他们一共去了几个成人?几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.
解:(1)设一共去了个成人,个学生,根据题意,得
解得
(2)如果购买团体票,需(元),这样可以节省14元,因此应该购买团体票更省钱.
课时作业:
A等级
1.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是 g.
2.如图,某商场正在热销2008年北京奥运会的纪念品,小华买了一盒福娃和一枚奥运徽章,已知一盒福娃的价格比一枚奥运徽章的价格贵120元,则一盒福娃价格是 元.
3.足球联赛得分规定如图,大地足球队在足球联赛的5场比赛中得8分,则这个队比赛的胜、平、负的情况是 .
4.若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需 元.
5.为了奖励兴趣小组的同学,张老师花92元钱购买了《智力大挑战》和《数学趣题》两种书.已知《智力大挑战》每本18元.《数学趣题》每本8元,则《数学趣题》买了 本.
6.根据北京奥运票务网站公布的女子双人3米跳板跳水决赛的门票价格(如表1),小明预定了B等级、C等级门票共7张,他发现这7张门票的费用恰好可以预订3张A等级门票.问小明预定了B等级、C等级门票各多少张?
7.手牵着手,心连着心.2008年5月12日发生在四川汶川的特大地震灾害,牵动着全中国人民的心.某校团支部发出为灾区捐款的倡议后,全校师生奉献爱心,踊跃捐款,已知全校师生共捐款4万5千元,其中学生捐款数比老师捐款数的2倍少9千元,该校老师和学生各捐款多少元?
8.“5·12”汶川大地震后,灾区急需大量帐篷。某服装厂原有4条成衣生产线和5条童装生产线,工厂决定转产,计划用3天时间赶制1000顶帐篷支援灾区。若启用1条成衣生产线和2条童装生产线,一天可以生产帐篷105顶;若启用2条成衣生产线和3条童装生产线,一天可以生产帐篷178顶.
(1)每条成衣生产线和童装生产线平均每天生产帐篷各多少顶?
(2)工厂满负荷全面转产,是否可以如期完成任务?如果你是厂长,你会怎样体现你的社会责任感?
9.小明和小东各有课外读物若干本,小明课外读物的数量是小东的2倍.小明送给小东10本后,小东课外读物的数量是小明剩余数量的3倍,求小明和小东原来各有课外读物多少本.
10.如图所求,小强和小红一起搭积木.小强所搭的“小塔”高度为23cm,小红所搭的“小树”高度为22cm.设每块A型积木的高为cm,每块B型积木的高为cm,请求出和的值.
B等级
1.中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则与2个球体相等质量的正方体的个数为( )
A.5 B.4
C.3 D.2
2.为紧急安置100名地震灾民,需要同时搭建可容纳6人和4人的两种帐篷,则搭建方案共有( )
A.8种 B.9种 C.16种 D.17种
3.中央电视台2套“开心辞典”栏目,有一题的题目如图所示,两个天平都平衡,则三个球体的重量等于多少个正方体的重量( )
A.2个 B.3个 C.4个 D.5个
4.如果是同类项,那么a、b的值分别是( )
A. B. C. D.
5.已知、互余,比大.设、的度数分别为、,下列方程组中符合题意的是( )
A. B. C. D.
6.四川512大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷顶、乙种帐篷顶,那么下面列出的方程组中正确的是( )
A. B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
7.已知、互余,比大.设、的度数分别为、,下列方程组中符合题意的是( )
A. B. C. D.
8.为确保信息安全,信息需要加密传输,发送方将明文加密传输给接收方,接收方收到密文后解密还原为明文,已知某种加密规则为:明文a,b对应的密文为,,例如1,2对应的密文是,4,当接收方收到的密文是1,7时,解密得到的明文是( )
A.,1 B. 1,1 C. 1,3 D. 3,1
C等级
1.5·12汶川大地震引起山体滑坡堵塞河谷后,形成了许多堰塞湖. 据中央电视台报道:唐家山堰塞湖危险性最大. 为了尽快排除险情,决定在堵塞体表面开挖一条泄流槽, 经计算需挖出土石方13.4万立方米,开挖2天后,为了加快施工进度,又增调了大量的人员和设备,每天挖的土石方比原来的2倍还多1万立方米,结果共用5天完成任务,比计划时间大大提前.
根据以上信息,求原计划每天挖土石方多少万立方米?增调人员和设备后每天挖土石方多少万立方米?
2.四川的强烈地震,牵动着花蕊小朋友的心. 花蕊小朋友用280元,买了每支元的铅笔和每支5元的钢笔一共200支,寄给灾区的小朋友,请你计算出她买的铅笔和钢笔的支数.
3.在一次春游中,小明、小亮等同学随家人一同到江郎山旅游,下面是购买门票时,小明与他爸爸的对话(如图所示).
(1)小明他们一共去了几个成人?几个学生?
(2)请你帮助小明算一算,用哪种方式买票更省钱?并说明理由.
4.为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
5.教师节来临之际,群群所在的班级准备向每位辛勤工作的教师献一束鲜花,每束由4支鲜花包装而成,其中有象征母爱的康乃馨和象征尊敬的水仙花两种鲜花,同一种鲜花每支的价格相同.请你根据第一、二束鲜花提供的信息,求出第三束鲜花的价格.
6.实验中学组织爱心捐款支援灾区活动,九年级一班55名同学共捐款1180元,捐款情况见下表.表中捐款10元和20元的人数不小心被墨水污染已经看不清楚,请你帮助确定表中的数据.
捐款(元) 5 10 20 50
人数 6 7
7.汶川大地震发生后,各地人民纷纷捐款捐物支援灾区.我市某企业向灾区捐助价值94万元的A,B两种帐篷共600顶.已知A种帐篷每顶1700元,B种帐篷每顶1300元,问A,B两种帐篷各多少顶?
8.据研究,当洗衣机中洗衣粉的含量在0.2%~0.5%之间时,衣服的洗涤效果较好,因为这时表面活性较大.
现将4.94kg的衣服放入最大容量为15kg的洗衣机中,欲使洗衣机中洗衣粉的含量达到,那么洗衣机中需要加入多少千克水,多少匙洗衣粉?(1匙洗衣粉约0.02kg,假设洗衣机以最大容量洗涤)
9.暑假期间,小明到父亲经营的小超市参加社会实践活动.一天小明随父亲从银行换回来58张、共计200元的零钞用于顾客付款时找零.细心的小明清理了一下,发现其中面值为1元的有20张,面值为10元的有7张,剩下的均为2元和5元的钞票.你能否用所学的数学方法算出2元和5元的钞票各有多少张吗?请写出演算过程.
10.课本中介绍我国古代数学名著《孙子算经 ( http: / / www.21cnjy.com / )》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头(只)?
如果假设鸡有只,兔有只,请你写出关于的二元一次方程组;并写出你求解这个方程组的方法.
课时作业答案:
A等级答案:
1:20
2:145
3:胜2场平2场负1场
4:12
5:7
6.设小明预订了B等级,C等级门票分别为x张和y张.
依题意,得
解这个方程组得
答:小明预订了B等级门票3张,C等级门票4张.
7:解:设老师捐款元,学生捐款元,则有
解得
答:该校老师捐款18000元,学生捐款27000元.
8:(1)设每条成衣生产线和童装生产线平均每天生产帐篷各x、y顶,则 , 解得x=41,y=32.
答:每条成衣生产线平均每天生产帐篷41顶,每条童装生产线平均每天生产帐篷32顶。
(2)由3(4×41+5×32)=972<1000知,即使工厂满负荷全面转产,还不能如期完成任务。
可以从加班生产、改进技术等方面进一步挖掘生产潜力,或者动员其它厂家支援等,想法尽
早完成生产任务,为灾区人民多做贡献.
9:解:设小明原来有课外读物本,小东原来有课外读物本.
则HYPERLINK "http://www.21cnjy.com/"EMBED Unknown
解得
答:小明原来有课外读物156本,小东原有课外读物8本.
10:解:根据题意,得
解得HYPERLINK "http://www.21cnjy.com/"EMBED Unknown
答:为4,为5.
B等级答案:
1:A
2:A
3:D
4:A
5:C
6:D
7:D
8:C
C等级答案:
1:解:设原计划每天挖土石方x万立方米,增调人员和设备后每天挖y万立方米
可列出方程组:
解之得:
答:原计划每天挖土石方1.3万立方米,增调人员和设备后每天挖3.6万立方米
2:解:设买的铅笔为x支,买的钢笔为y支.
根据题意得:
解得
答:略
3:解:(1)设小明他们一共了个成人,个学生,
答:小明他们一共去了7个成人,4个学生.
(2)若按14人购买团体票,则共需(元)
(元).
购买团体票可省24元. 3分
4:解:设生产奥运会标志x套,生产奥运会吉祥物y套.根据题意,得
①×2-②得:5x=10000.
∴ x=2000.
把x=2000代入①得:5y=12000.
∴ y=2400.
答:该厂能生产奥运会标志2000套,生产奥运会吉祥物2400套.
5:解:设康乃馨每支元,水仙花每支元
由题意得:
解得:
第三束花的价格为
答:第三束花的价格是17元.
6:解:设捐10元的同学有人,捐20元的同学有人,根据题意,得
化简,得
解这个方程组,得
答:捐款10元和20元的同学分别为4人和38人. 7分
7:解:设A种帐篷x顶,B种帐篷y顶,根据题意,列方程组
解,得
∴ A种帐篷400顶,B种帐篷200顶.
8:解:设洗衣机中需加入千克水,匙洗衣粉.
由题意得
解得
所以,洗衣机中需加入10千克水,3匙洗衣粉.
9:解:设面值为2元的有x张,设面值为2元的有y张,依题意得
解得
经检验,符合题意
答:面值为2元的有16张,设面值为2元的有15张.
10:方程组如下: ,
可以用代入消元和加减消元法来解这个方程组.
13cm
14cm
高
长
宽
共计145元
共计280元
年
级
项
目
我知道随身听的单价比书包的单价的4倍少8元.
我知道随身听和书包的单价之和是452元.
哎,我们家今年菠萝收入多少钱呢?
老李,没关系。你看我们家去年只净赚8000元,今年却净赚11800元。增加投资值得!
阿菊,我算了一下,今年我们家菠萝的收比去年增加了35%,不过投资也增加了10%
小明
老李
阿菊
图1
图2
公司
计算器单价
(单位:元)
型:60
型:40
型:25
型:50
型:20
甲品牌
乙品牌
乙
图2
2m
30cm
50cm
A
2.5m
40cm
60cm
70cm
3m
50cm
图5
巧克力
果冻
50g砝码
一共花了170元
xcm
ycm
A
B
B
B
B
B
B
A
A
A
A
A
小强
小红
共计19元
共计18元
第三束
水仙花
康乃馨
①
②
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第八章 二元一次方程组
第10课时 二元一次方程组的应用
对于二元一次方程组的应用问题,关键是由实际问题向数学问题的转化过程。所以在教学过程中注重分析问题的方法,让学生学会用数学建模的思想和方程的思想来解决问题。例题的选取也是从实际出发,让学生初步体会到数学与人们的日常生活的密切关系,并体会数学在社会生活中所起的作用,激发学生对数学的学习兴趣,使学生学会从数学的角度去分析和解决简单的实际问题。
二元一次方程组的应用,是在学习了二元一次方程组解法的基础上进行的,在生活实践和数学领域里有着非常广泛的应用。重点是列二元一次方程组解决实际问题.难点是在实际问题中找等量关系、列方程组.
点击一:列二元一次方程组解应用题的一般步骤可概括为“审、找、列、解、答”五步,即:
(1)审:通过审题,把实际问题抽象成数学问题,分析已知数和未知数,并用字母表示其中的两个未知数;
(2)找:找出能够表示题意两个相等关系;
(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;
(4)解:解这个方程组,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案.
针对练习:
1.某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,问中、小型汽车各有多少辆?
2.某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 直接销售 粗加工后销售 精加工后销售
每吨获利(元) 100 250 450
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行).
(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 全部直接销售 全部粗加工后销售 尽量精加工,剩余部分直接销售
获利(元)
(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?
3.为满足市民对优质教育的需求,某中学决定改变办学条件,计划拆除一部分旧校舍,建造新校舍,拆除旧校舍每平方米需80元,建新校舍每平方米需700元. 计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿地面积,新建校舍只完成了计划的80%,而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.
(1)求:原计划拆、建面积各是多少平方米?
(2)若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?
答案:1.解:设中型汽车有x辆,小型汽车有y辆.由题意,得
解得,
故中型汽车有15辆,小型汽车有35辆.
2.解:(1)全部直接销售获利为:100×140=14000(元);
全部粗加工后销售获利为:250×140=35000(元);
尽量精加工,剩余部分直接销售获利为:450×(6×18)+100×(140-6×18)=51800(元).
(2)设应安排x天进行精加工, y天进行粗加工.
由题意,得
3.(1)原计划拆、建面积各是4800平方米、2400平方米;
(2)可绿化面积为1488平方米.
解得,
故应安排10天进行精加工,5天进行粗加工.
类型之一:图形信息题
例1.扬子江药业集团生产的某种药品包装盒的侧面展开图如图所示.如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.
解析:要求包装盒的体积,必须先求出这种包装盒的长、宽、高,由于长方体盒子的长比宽多4cm,因此可设宽为,高为后列二元一次方程组求解.
解:设这种药品包装盒的宽为,高为,则长为,
根据题意得,
解这个方程组得
故长为9cm,宽为5cm,高为2cm.
体积
答:这种药品包装盒的体积为.
类型之二:图画信息题
例2.某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少元?
解析:本题的条件由图画给出,形式新颖,这也是近几年二元一次方程组应用的常见题型.
解:设一盒“福娃”玩具和一枚徽章的价格分别为元和元.
依题意,得
解这个方程组,得
答:一盒“福娃”玩具和一枚徽章的价格分别为元和元.
类型之三:残缺信息题
例3.国家为九年义务教育期间的学生实行“两免一补”政策,下表是我市某中学国家免费提供教科书补助的部分情况.
七 八 九 合计
每人免费补助金额(元) 110 90 50
人数(人) 80 300
免费补助总金额(元) 4000 26200
如果要知道空白处的数据,可设七年级的人数为,八年级的人数为,根据题意列出方程组为( )
A. B.
C. D.
解析:本题的信息残缺,但由表中给出的其他信息可求解,答案D.
类型之四:对话信息题
例4.小英和小强相约一起去某超市购买他们看中的随身听和书包.你能根据他们的对话内容(如图),求出他们看中的随身听和书包单价各是多少元吗?
解:设他们看中的书包的单价为元,随身听的单价为元.
依题意有
解得
答:(略)
类型之五:表格信息型
例5 某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 西红柿 豆角
批发价(单位:元/㎏) 1.2 1.6
零售价(单位:元/㎏) 1.8 2.5
问:他当天卖完这些西红柿和豆角能赚多少钱?
(无锡市中考题)
解析:由表中提供的数据可知每斤西红柿批发价1.2元/㎏,零售价1.8元/㎏,净赚0.6元/㎏;每斤豆角批发价1.6元/㎏,零售价2.5元/㎏,净赚0.9元/㎏。利用上述信息找出等量关系列方程组求解。
解:设批发西红柿xkg,批发豆角ykg,则卖完净赚(0.6x+0.9y)元,根据题意得
解得
∴0.6x+0.9y=0.6×10+0.9×30=33(元)
答:他当天卖完这些西红柿和豆角能赚33元钱。
类型之六:情景对话型
例6 在当地农业技术部门指导下,小明家增加种植菠萝的投资,使今年的菠萝喜获丰收。下面是小明爸爸、妈妈的一段对话。
请你用学过的知识帮助小明算出他们家今年菠萝的收入。(收入-投资=净赚)
(海南省中考题)
解:设小明家去年种植菠萝的收入为x元,投资为y元,根据题意得
解得
∴小明家今年菠萝的收入应为:
(1+35%)x=1.35×12000=16200元
类型之七:解答说理型
例7 随着我国人口增长速度的减慢,小学入学儿童数量每年按逐渐减少的趋势发展。某区2003年和2004年小学儿童人数之比为8:7,且2003年入学人数的2倍比2004年入学人数的3倍少1500人。某人估计2005年入学儿童数将超过2300人。请你通过计算,判断他的估计是否符合当前的变化趋势。
(吉林省中考题)
解:设2003年入学儿童人数为x人,2004年入学儿童人数y人,根据题意得
解得
∵2300>2100
∴他估计不符合当前入学儿童逐渐减少的趋势。
类型之八:几何拼图型
例8 如图1,图2,是由8个一样大小的小长方形拼成的,且图2中的小正方形(阴影部分)的面积为1cm2,求小长方形的长和宽。
(大连市中考题)
解析:小正方形面积为1cm2,则意味着它的边长为1cm,若再注意到矩形的长或宽的构成方式,则不难求出。本例着重考察学生的数形结合思想及方程建模能力。
解:设小长形的长为xcm,宽为ycm,根据题意,得
解得
答:小长形的长为5cm,宽为3cm。
类型之九:药品降价问题
例9:2001年以来,我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如表二所示,表中缺失了2003年、2007年相关数据.已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额.
年份 2001 2003 2004 2005 2007
降价金额(亿元) 54 35 40
表二
解析 要求2003年和2007年的药品降价金额.设2003年和2007年的药品降价金额分别为亿元、亿元,由表中提供的信息即可根据题意即可列出二元一次方程组求解.
解:设2003年和2007年的药品降价金额分别为亿元、亿元.
根据题意, ( http: / / www.21cnjy.com / )
解方程组,得 ( http: / / www.21cnjy.com / )
答:2003年和2007年的药品降价金额分别为20亿元和120亿元.
点评:当一个问题直接求解有困难时,不妨换一种思维,间接求解.本题中通过先分别求出红辣椒和西红柿的重量即可使问题获解.
类型之十:团体购票问题
例10:团体购买公园门票票价如下:
购票人数 1~50 51~100 100人以上
每人门票(元) 13元 11元 9元
今有甲、乙两个旅行团,已知甲团人数少于50人,乙团人数不超过100人.
若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计
应付门票费1080元.
(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
解析:本题以表格形式提供了部分信息,主要考查运用二元一次方程组解决实际问题的能力.
分析 由题意我们可得到列方程组的关系,这样就可列方程组求解.
解:(1)∵100×13=1300<1392
∴乙团的人数不少于50人,不超过100人
(2)设甲、乙两旅行团分别有x人、y人,
则 ( http: / / www.21cnjy.com / )
解得:
所以甲、乙两旅行团分别有36人、84人
点评:本题是一道列二元一次方程组的应用题,要注意结果是否是原方程组的解,解是否符合实际意义.
类型之十一:决策型问题
例11.某公司现有甲、乙两种品牌的计算器,甲品牌计算器有三种不同的型号,乙品牌计算器有两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
(1)写出所有的选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么型号计算器被选中的概率是多少?
(3)现知新华中学购买甲、乙两种品牌计算器共40个(价格如图所示),恰好用了1000元人民币,其中甲品牌计算器为型号计算器,求购买的型号计算器有多少个?
解:(1)树状图表示如下:
甲
列表表示如下:
有6种可能结果:.
说明:用其它方式表达选购方案且正确者,只给1分.
(2)因为选中型号计算器有2种方案,即,所以型号计算器被选中的概率是.
(3)由(2)可知,当选用方案时,设购买型号,型号计算器分别为个,
根据题意,得解得
经检验不符合题意,舍去;
当选用方案时,设购买型号、型号计算器分别为个,
根据题意,得解得
所以新华中学购买了5个型号计算器.
【点评】解这类问题,要求要读懂题意,获得正确的信息.是把实际决策问题转化为二元一次方程组来解决.即通过构建数学模型解决实际应用题,这是中考的热点问题
类型之十二:配套问题
例12:现有190张铁皮,每张铁皮可做8个盒身或做22个盒底,一个盒身与两个盒底配成一个完整盒子,那么用多少张铁皮制盒身,多少张铁皮制盒底,可以正好制成一批完整的盒子
解析:此题有两个未知量——制盒身、盒底的铁皮张数.
问题中有两个等量关系:⑴制盒身铁皮张数+制盒底铁皮张数=190;
⑵制成盒身的个数的2倍=制成盒底的个数.
解:设x张铁皮制盒身,y张铁皮制盒底,
根据题意,得
解这个方程组,得
答:110张制盒身,80张制盒底,可以正好制成一批完整的盒子.
一、选择题
1,某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏本20%,在这项买卖中,这家商店( )
A.赔了8元 B.赚了32元 C.不赔不赚 D.赚了8元
2,甲、乙两人相距42km,若相向而行,2小时相遇;若同向而行,乙14小时就能追上甲,则甲、乙二人每小时各走( )
A.12 km、9 km B.11 km、10 km
C.10 km、11 km D.9 km、12 km
3,一个两位数,对换它的十位数字与个位数字后,所得的数是原数的,则这样的两位数的个数有( )
A.0个 B.3个 C.4个 D.无数多个
4,已知 是方程5x-ky=3的一个解,则k-1=( )
A.0 B.1 C.2 D.3
5,为保护生态环境,我省某山区县响 国家“退耕还林”号召,将该县某地一部分耕地改为林地,改变后,林地面积和耕地面积共有180 平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各为多少平方千米,设耕地面积为x平方千米,林地面积为y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
A. B. C. D.
6,用化肥x千克给一块y公顷的麦地施肥,若每公顷用 化肥23千克,则还差90千克;若每公顷用化肥18千克,则还多余110千克,由题意,可列出方程组( )
A. B. C. D.
二、填空题
7,若实数m、n满足条件m+n=3,且m-n=1,则m=_____,n=_______.
8,已知二元一次方程组的解是则a+b的值为______.
9,已知等式(2A-7B)x+(3A-8B)=8x+10对一切实数x都成立,则A=___,B=___.
10,如果3a7xby+7和-7a2-4yb2x是同类项, 则x=_____,y=_____.
11,将若干只鸡放入若干个笼中,若每个笼中放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,则至少有___只鸡.
12,某山区有23名中、小学生因贫困失学需要捐助, 资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表:
初一年级 初二年级
捐款数额(元) 4 000 4 200
捐助贫困中学生人数(名) 2 3
捐助贫困小学生人数(名) 4 3
则a=___,b=___.
13,某校去年有学生1000名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x名,走读学生y名,则可列出方程组为 .
14,以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺,绳长、井深各几何?若设绳长x尺,井深y尺,则可列方程组为 .
三、解答题
15,仔细观察如图2,认真阅读对话:
根据以上对话内容,可知小明买5元邮票是多少张?
16,在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10 000辆”;
乙同学说:“四环路比三环路车流量每小时多2 000辆”;
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”.
请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少.
17,甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
18,有三把楼梯,分别是五步梯、七步梯、九步梯,每攀沿一步阶梯上升的高度是一致的.每把楼梯的扶杆长(即梯长)、顶档宽、底档宽如图3所示,并把横档与扶杆粘合处称作联结点(如点A).
(1)通过计算,补充填写下表:
楼梯种类 两扶杆总长(米) 横档总长(米) 联结点数(个)
五步梯 4 2.0 10
七步梯
九步梯
(2)一把楼梯的成本由材料费和加工费组成,假定加工费以每个个联结点1元计算,而材料费中扶杆的单价与横档的单价不相等(材料损耗及其它因素忽略不计).现已知一把五步梯、七步梯的成本分别是26元、36元,试求出一把九步梯的成本.
19,“利海”通讯器材商场,计划用60 000元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部1 800元,乙种型号手机每部600元 ,丙种型号手机每部1200元.若商场同时购进其中两种不同型号的手机共40部,并将60 000元恰好用完,请你帮助商场计算一下如何购买.
参考答案:
一、1,D;2,D;3,C;4,A;5,B;6,A.
二、7,m=2, n=1;8,把x=2,y=1代入原方程组,得 (1)+(2)得3(a+b)=9,∴a+b=3;9,由于等式(2A-7B)x+(3A-8B)=8x+10对一切实数x都成立,所以根据待定系数即可得到关于A、B的二元一次方程组,即解得10,x=2,y=-3;11,25;12,根据题意,得解这个方程组,得 13,;14,.
三、15,设小明买2元邮票x张,1元邮票2x张,5元邮票y张,则根据题意,得解得即小明买3张5元邮票.
16,设高峰时段三环路的车流量为每小时x辆,四环路的、车流量为每小时y辆.根据题意,得 解这个方程组,得 答:高峰时段三环路的车流量为每小时11 000辆,四环路的车流量为每小时13 000辆;
17,设甲、乙两件服装的成本分别是x元、y元.根据题意,得
解这个方程组,得答 甲、乙两件服装的成本分别是300元、200元.
18,(1)七步梯、九步梯的扶杆长分别是5米、6米;横档总长分别是3.5米、3.5米;联结点个数分别是14个、18个.(2)设扶杆单价为x元/米,横档单价为y元/米.依题意得:即解得故九步梯的成本为6×3+5.4×2+1×18=46.8(元)即一把九步梯的成本为46.8元.
19,设甲种型号手机要购买x部,乙种型号手机要购买y部,丙种型号手机要购买z部,根据题意,得或
或分别解这三个方程组,得 或 或 (不合题意,舍去)答 有两种购买方法:甲种型号手机购买30部,乙种型号手机购买10部;或甲种型号手机购买20部,丙种型号手机购买20部.
一、耐心填一填,一锤定音!(每小题6分,共30分)
1.在方程中,如果是它的一个解,那么的值为______.
2.大数和小数的差为,这两个数的和为,则大数是______,小数是______.
3.买支铅笔和本练习本,共用元.若铅笔每支元,练习本每本元,写出以和为未知数的方程为______.
4.甲、乙两人速度之比是,则他们在相同时间内走过的路程之比是______,他们在走相同路程所需时间之比是______.
5.羊圈里白羊的只数比黑羊的脚数少,黑羊的只数比白羊的脚数少,则白羊有______只,黑羊有______只.
二、精心选一选,慧眼识金!(每小题5分,共15分)
1.既是方程的解,又是方程的解是( )
A. B. C. D.
2.甲、乙两数这和为,甲数的倍等于乙数的倍,若设甲数为,乙数为,则方程组(1)(2)(3)(4)中,正确的有( )
A.组 B.组 C.组 D.组
3.某校名学生参加竞赛,平均分为分,其中及格学生平均分为分,不及格学生平均分为分,则不及格学生的人数为( )
A. B. C. D.
三、用心做一做,马到成功!(本大题共20分)
1.(本题10分)根据下图提供的信息,求每件恤衫和每瓶矿泉水的价格.
2.(本题10分)小明到商店买东西,下面是他和售货员阿姨的对话:“我买这种牙膏支,这种牙刷把”.“一共元角”.付款后,小明说:“阿姨,这支牙膏我不要了,换一把牙刷吧!”“还需找你元”.从他们的对话中你能知道牙刷、牙膏的单价吗?
四、综合运用,再接再厉!(本大题共35分)
1.(本题11分)如图,周长为的长方形被分成个相同的长方形,求长方形的长和宽.
2.(本题12分)长沙市某公园的门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
票价 10元/人 8元/人 5元/人
某校七年级甲、乙两班共多人去该公园举行联欢活动,其中甲班多人,乙班不足人.如果以班为单位分别买票,两个班一共应付元;如果两个班联合起来作为一团体购票,一共只要付元.问:甲、乙两班分别有多少人?
3.(本题12分)有甲、乙、丙三种规格的钢条,已知甲种根,乙种根,丙种根,共长米;甲种根,乙种根,丙种根共长米,问甲根,乙根,丙根共长多少?
参考答案
一、1. 2., 3. 4., 5.,
二、1.B 2.C 3.D
三、1., 2.,
四、1., 2., 3.米
1.某酒店客房部有三人间、双人间客房,收费数据如下表.
普通(元/间/天) 豪华(元/间/天)
三人间 150 300
双人间 140 400
为吸引游客,实行团体入住五折优惠措施.一个50人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房.若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人间和双人普通间客房和多少间?
解:设三人普通房和双人普通房各住了,间,根据题意,得
解得答:略.
聪明的你还能怎样设未知数解答本题呢?
2.根据右图提供的信息,求出每支网球拍的单价为__元,每支乒乓球拍的单价为__元.
解:设每支网球拍元,每支乒乓球拍元,根据题意,得
解得
3.
解:设1本笔记本元,1支钢笔元,根据题意,得
EMBED Equation.3 解得答:略.
4.在“五一”黄金周期间,小明、小亮等同学随家人一同到江郎山游玩.下面是购买门票时,小明与
他爸爸的对话:
问题:(1)小明他们一共去了几个成人?几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.
解:(1)设一共去了个成人,个学生,根据题意,得
解得
(2)如果购买团体票,需(元),这样可以节省14元,因此应该购买团体票更省钱.
课时作业:
A等级
1.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是 g.
2.如图,某商场正在热销2008年北京奥运会的纪念品,小华买了一盒福娃和一枚奥运徽章,已知一盒福娃的价格比一枚奥运徽章的价格贵120元,则一盒福娃价格是 元.
3.足球联赛得分规定如图,大地足球队在足球联赛的5场比赛中得8分,则这个队比赛的胜、平、负的情况是 .
4.若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需 元.
5.为了奖励兴趣小组的同学,张老师花92元钱购买了《智力大挑战》和《数学趣题》两种书.已知《智力大挑战》每本18元.《数学趣题》每本8元,则《数学趣题》买了 本.
6.根据北京奥运票务网站公布的女子双人3米跳板跳水决赛的门票价格(如表1),小明预定了B等级、C等级门票共7张,他发现这7张门票的费用恰好可以预订3张A等级门票.问小明预定了B等级、C等级门票各多少张?
7.手牵着手,心连着心.2008年5月12日发生在四川汶川的特大地震灾害,牵动着全中国人民的心.某校团支部发出为灾区捐款的倡议后,全校师生奉献爱心,踊跃捐款,已知全校师生共捐款4万5千元,其中学生捐款数比老师捐款数的2倍少9千元,该校老师和学生各捐款多少元?
8.“5·12”汶川大地震后,灾区急需大量帐篷。某服装厂原有4条成衣生产线和5条童装生产线,工厂决定转产,计划用3天时间赶制1000顶帐篷支援灾区。若启用1条成衣生产线和2条童装生产线,一天可以生产帐篷105顶;若启用2条成衣生产线和3条童装生产线,一天可以生产帐篷178顶.
(1)每条成衣生产线和童装生产线平均每天生产帐篷各多少顶?
(2)工厂满负荷全面转产,是否可以如期完成任务?如果你是厂长,你会怎样体现你的社会责任感?
9.小明和小东各有课外读物若干本,小明课外读物的数量是小东的2倍.小明送给小东10本后,小东课外读物的数量是小明剩余数量的3倍,求小明和小东原来各有课外读物多少本.
10.如图所求,小强和小红一起搭积木.小强所搭的“小塔”高度为23cm,小红所搭的“小树”高度为22cm.设每块A型积木的高为cm,每块B型积木的高为cm,请求出和的值.
B等级
1.中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则与2个球体相等质量的正方体的个数为( )
A.5 B.4
C.3 D.2
2.为紧急安置100名地震灾民,需要同时搭建可容纳6人和4人的两种帐篷,则搭建方案共有( )
A.8种 B.9种 C.16种 D.17种
3.中央电视台2套“开心辞典”栏目,有一题的题目如图所示,两个天平都平衡,则三个球体的重量等于多少个正方体的重量( )
A.2个 B.3个 C.4个 D.5个
4.如果是同类项,那么a、b的值分别是( )
A. B. C. D.
5.已知、互余,比大.设、的度数分别为、,下列方程组中符合题意的是( )
A. B. C. D.
6.四川512大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷顶、乙种帐篷顶,那么下面列出的方程组中正确的是( )
A. B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
7.已知、互余,比大.设、的度数分别为、,下列方程组中符合题意的是( )
A. B. C. D.
8.为确保信息安全,信息需要加密传输,发送方将明文加密传输给接收方,接收方收到密文后解密还原为明文,已知某种加密规则为:明文a,b对应的密文为,,例如1,2对应的密文是,4,当接收方收到的密文是1,7时,解密得到的明文是( )
A.,1 B. 1,1 C. 1,3 D. 3,1
C等级
1.5·12汶川大地震引起山体滑坡堵塞河谷后,形成了许多堰塞湖. 据中央电视台报道:唐家山堰塞湖危险性最大. 为了尽快排除险情,决定在堵塞体表面开挖一条泄流槽, 经计算需挖出土石方13.4万立方米,开挖2天后,为了加快施工进度,又增调了大量的人员和设备,每天挖的土石方比原来的2倍还多1万立方米,结果共用5天完成任务,比计划时间大大提前.
根据以上信息,求原计划每天挖土石方多少万立方米?增调人员和设备后每天挖土石方多少万立方米?
2.四川的强烈地震,牵动着花蕊小朋友的心. 花蕊小朋友用280元,买了每支元的铅笔和每支5元的钢笔一共200支,寄给灾区的小朋友,请你计算出她买的铅笔和钢笔的支数.
3.在一次春游中,小明、小亮等同学随家人一同到江郎山旅游,下面是购买门票时,小明与他爸爸的对话(如图所示).
(1)小明他们一共去了几个成人?几个学生?
(2)请你帮助小明算一算,用哪种方式买票更省钱?并说明理由.
4.为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
5.教师节来临之际,群群所在的班级准备向每位辛勤工作的教师献一束鲜花,每束由4支鲜花包装而成,其中有象征母爱的康乃馨和象征尊敬的水仙花两种鲜花,同一种鲜花每支的价格相同.请你根据第一、二束鲜花提供的信息,求出第三束鲜花的价格.
6.实验中学组织爱心捐款支援灾区活动,九年级一班55名同学共捐款1180元,捐款情况见下表.表中捐款10元和20元的人数不小心被墨水污染已经看不清楚,请你帮助确定表中的数据.
捐款(元) 5 10 20 50
人数 6 7
7.汶川大地震发生后,各地人民纷纷捐款捐物支援灾区.我市某企业向灾区捐助价值94万元的A,B两种帐篷共600顶.已知A种帐篷每顶1700元,B种帐篷每顶1300元,问A,B两种帐篷各多少顶?
8.据研究,当洗衣机中洗衣粉的含量在0.2%~0.5%之间时,衣服的洗涤效果较好,因为这时表面活性较大.
现将4.94kg的衣服放入最大容量为15kg的洗衣机中,欲使洗衣机中洗衣粉的含量达到,那么洗衣机中需要加入多少千克水,多少匙洗衣粉?(1匙洗衣粉约0.02kg,假设洗衣机以最大容量洗涤)
9.暑假期间,小明到父亲经营的小超市参加社会实践活动.一天小明随父亲从银行换回来58张、共计200元的零钞用于顾客付款时找零.细心的小明清理了一下,发现其中面值为1元的有20张,面值为10元的有7张,剩下的均为2元和5元的钞票.你能否用所学的数学方法算出2元和5元的钞票各有多少张吗?请写出演算过程.
10.课本中介绍我国古代数学名著《孙子算经 ( http: / / www.21cnjy.com / )》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头(只)?
如果假设鸡有只,兔有只,请你写出关于的二元一次方程组;并写出你求解这个方程组的方法.
课时作业答案:
A等级答案:
1:20
2:145
3:胜2场平2场负1场
4:12
5:7
6.设小明预订了B等级,C等级门票分别为x张和y张.
依题意,得
解这个方程组得
答:小明预订了B等级门票3张,C等级门票4张.
7:解:设老师捐款元,学生捐款元,则有
解得
答:该校老师捐款18000元,学生捐款27000元.
8:(1)设每条成衣生产线和童装生产线平均每天生产帐篷各x、y顶,则 , 解得x=41,y=32.
答:每条成衣生产线平均每天生产帐篷41顶,每条童装生产线平均每天生产帐篷32顶。
(2)由3(4×41+5×32)=972<1000知,即使工厂满负荷全面转产,还不能如期完成任务。
可以从加班生产、改进技术等方面进一步挖掘生产潜力,或者动员其它厂家支援等,想法尽
早完成生产任务,为灾区人民多做贡献.
9:解:设小明原来有课外读物本,小东原来有课外读物本.
则HYPERLINK "http://www.21cnjy.com/"EMBED Unknown
解得
答:小明原来有课外读物156本,小东原有课外读物8本.
10:解:根据题意,得
解得HYPERLINK "http://www.21cnjy.com/"EMBED Unknown
答:为4,为5.
B等级答案:
1:A
2:A
3:D
4:A
5:C
6:D
7:D
8:C
C等级答案:
1:解:设原计划每天挖土石方x万立方米,增调人员和设备后每天挖y万立方米
可列出方程组:
解之得:
答:原计划每天挖土石方1.3万立方米,增调人员和设备后每天挖3.6万立方米
2:解:设买的铅笔为x支,买的钢笔为y支.
根据题意得:
解得
答:略
3:解:(1)设小明他们一共了个成人,个学生,
答:小明他们一共去了7个成人,4个学生.
(2)若按14人购买团体票,则共需(元)
(元).
购买团体票可省24元. 3分
4:解:设生产奥运会标志x套,生产奥运会吉祥物y套.根据题意,得
①×2-②得:5x=10000.
∴ x=2000.
把x=2000代入①得:5y=12000.
∴ y=2400.
答:该厂能生产奥运会标志2000套,生产奥运会吉祥物2400套.
5:解:设康乃馨每支元,水仙花每支元
由题意得:
解得:
第三束花的价格为
答:第三束花的价格是17元.
6:解:设捐10元的同学有人,捐20元的同学有人,根据题意,得
化简,得
解这个方程组,得
答:捐款10元和20元的同学分别为4人和38人. 7分
7:解:设A种帐篷x顶,B种帐篷y顶,根据题意,列方程组
解,得
∴ A种帐篷400顶,B种帐篷200顶.
8:解:设洗衣机中需加入千克水,匙洗衣粉.
由题意得
解得
所以,洗衣机中需加入10千克水,3匙洗衣粉.
9:解:设面值为2元的有x张,设面值为2元的有y张,依题意得
解得
经检验,符合题意
答:面值为2元的有16张,设面值为2元的有15张.
10:方程组如下: ,
可以用代入消元和加减消元法来解这个方程组.
13cm
14cm
高
长
宽
共计145元
共计280元
年
级
项
目
我知道随身听的单价比书包的单价的4倍少8元.
我知道随身听和书包的单价之和是452元.
哎,我们家今年菠萝收入多少钱呢?
老李,没关系。你看我们家去年只净赚8000元,今年却净赚11800元。增加投资值得!
阿菊,我算了一下,今年我们家菠萝的收比去年增加了35%,不过投资也增加了10%
小明
老李
阿菊
图1
图2
公司
计算器单价
(单位:元)
型:60
型:40
型:25
型:50
型:20
甲品牌
乙品牌
乙
图2
2m
30cm
50cm
A
2.5m
40cm
60cm
70cm
3m
50cm
图5
巧克力
果冻
50g砝码
一共花了170元
xcm
ycm
A
B
B
B
B
B
B
A
A
A
A
A
小强
小红
共计19元
共计18元
第三束
水仙花
康乃馨
①
②
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
