导数的几何意义
图片预览




文档简介
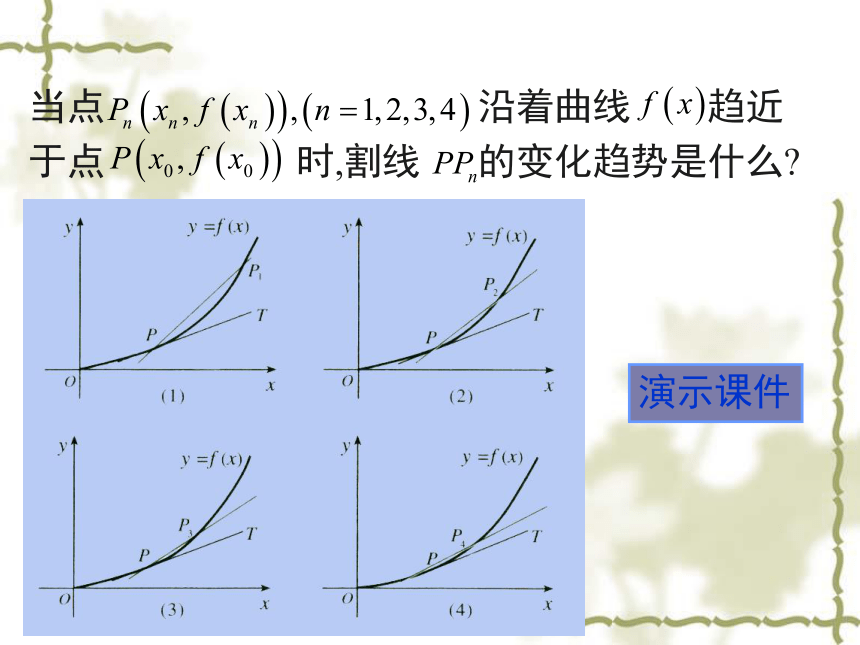
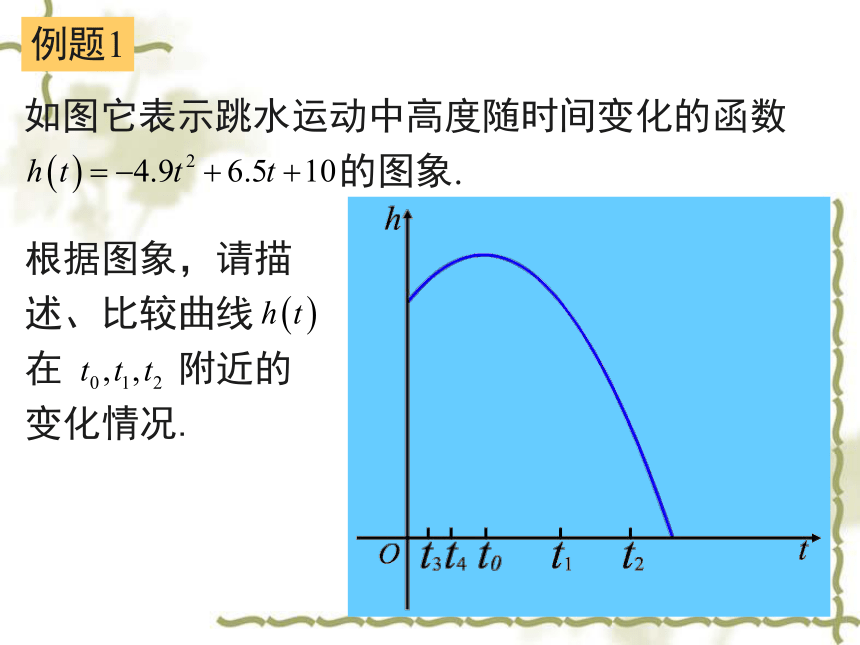
课件17张PPT。导数的几何意义课题岳阳市四中 喻樵夫复习提问导数的定义:在 的导数:导数 表示函数 在 处的瞬时变化率,反映函数 在 附近的变化情况。那么导数 的几何意义是什么呢?当点 沿着曲线 趋近于点 时,割线 的变化趋势是什么?演示课件 所以,函数 在 处的导数 的几何意义是;曲线 在 处的切线的斜率。 当点 趋近于点P时,割线 趋近于确定的位置,这个确定位置的直线 称为过点 的切线. 割线 的斜率与切线 的斜率 有什么关系呢? 的斜率例题1解:例题1讲解用曲线 在 处的切线,刻画曲线 在上述三个时刻附近的变化情况.(1)当 时,曲线 在 处的切线 平行于x轴.所以,在 附近曲线比较平坦,几乎没有升降.
(2)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.
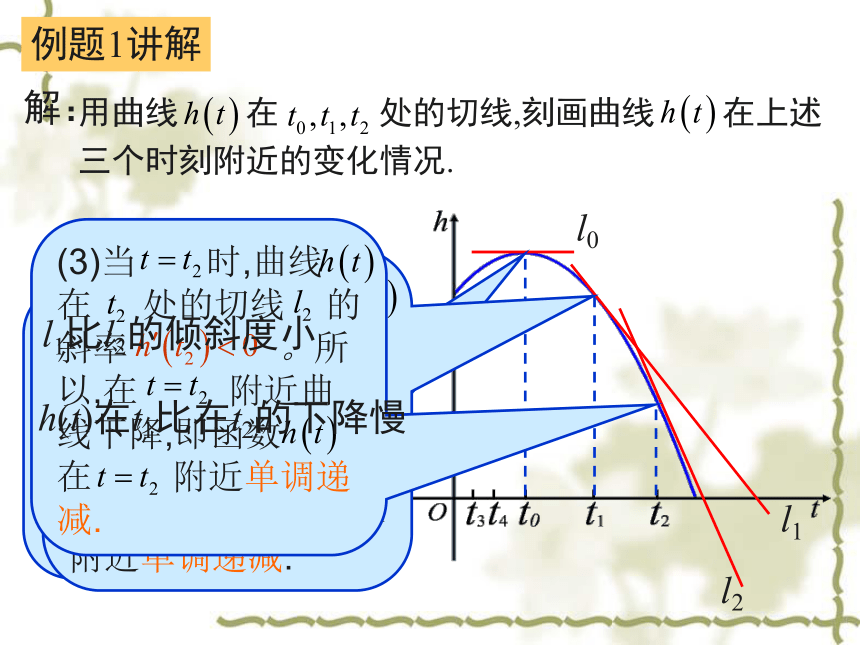
(3)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.l1比l2的倾斜度小h(t)在t1比在t2的下降慢(2)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.(3)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.用曲线 在 处的切线,刻画曲线 在上述三个时刻附近的变化情况.(1)当 时,曲线 在 处的切线 平行于x轴.所以,在 附近曲线比较平坦,几乎没有升降.解:例题1讲解练习描述函数 在 和 附近增(减)以及增(减)快慢的情况.(1)当 时,曲线 在 处的切线 的斜率 .所以,在 附近曲线上升,即函数 在 附近单调递增.(2)当 时,曲线 在 处的切线 的斜率 .所以,在 附近曲线上升,即函数 在 附近单调递增. 比 的倾斜度大, 在 比在 的上升快函数y=f(x)在x=x0处的导数 f ?(x0)的几何意义;(1)函数 在 处的导数 的几何意义是;曲线 在 处的切线的斜率。(2)若 f ?(x0)>0.所以,在 附近曲线上升,即函数 f (x)在 附近单调递增.(3)若 f ?(x0)<0.所以,在 附近曲线下降,即函数 f (x)在 附近单调递减. 如图,它表示人体血管中药物浓度c=f(t)(单位:mg/ml)随时间t (单位:min)变化的函数.根据图象,估计 t=0.2,0.4, 0.6,0.8min时,血管中药物浓度的瞬时变化率(精确到0.1).例题2根据导数的含义,血管中某一时刻药物浓度的瞬时变化率就是函数 f (t)在此时刻的导数.由于不知道函数c=f (t)的解析式,因而无法直接计算出函数 f (t)在此时刻的导数.但根据函数 c=f (t)的图象,由导数的几何意义知,函数f(t)在此时刻的导数就是对应点处切线的斜率. 画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此时刻药物浓度瞬时变化率的近似值.解:例题2讲解.并画出曲线求函数 在 处的导数, 例题3讲解解: 在区间 上的平均变化率为:
令 趋于零。知函数 在 处的导数为数。曲线 在 处的切线为 ,如右图当x=x0时,f ?(x0)是一个确定的数.
当x变化时, f ?(x)便是一个函数,称它为f (x)的导函数(简称导数)y=f (x)的导数有时也记作y?导函数的概念小结函数 f (x)在x=x0处的导数 f ?(x0)f ?(x0)几何意义:(2)若 f ?(x0)>0.函数 f (x)在 x=x0附近单调递增.(3)若 f ?(x0)<0.函数 f (x)在 x=x0附近单调递减.(1)函数 在 处的导数 的几何意义是;曲线 在 处的切线的斜率。作业课本第80习题3.1A组题5,6谢谢指导
(2)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.
(3)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.l1比l2的倾斜度小h(t)在t1比在t2的下降慢(2)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.(3)当 时,曲线 在 处的切线 的斜率 。所以,在 附近曲线下降,即函数 在 附近单调递减.用曲线 在 处的切线,刻画曲线 在上述三个时刻附近的变化情况.(1)当 时,曲线 在 处的切线 平行于x轴.所以,在 附近曲线比较平坦,几乎没有升降.解:例题1讲解练习描述函数 在 和 附近增(减)以及增(减)快慢的情况.(1)当 时,曲线 在 处的切线 的斜率 .所以,在 附近曲线上升,即函数 在 附近单调递增.(2)当 时,曲线 在 处的切线 的斜率 .所以,在 附近曲线上升,即函数 在 附近单调递增. 比 的倾斜度大, 在 比在 的上升快函数y=f(x)在x=x0处的导数 f ?(x0)的几何意义;(1)函数 在 处的导数 的几何意义是;曲线 在 处的切线的斜率。(2)若 f ?(x0)>0.所以,在 附近曲线上升,即函数 f (x)在 附近单调递增.(3)若 f ?(x0)<0.所以,在 附近曲线下降,即函数 f (x)在 附近单调递减. 如图,它表示人体血管中药物浓度c=f(t)(单位:mg/ml)随时间t (单位:min)变化的函数.根据图象,估计 t=0.2,0.4, 0.6,0.8min时,血管中药物浓度的瞬时变化率(精确到0.1).例题2根据导数的含义,血管中某一时刻药物浓度的瞬时变化率就是函数 f (t)在此时刻的导数.由于不知道函数c=f (t)的解析式,因而无法直接计算出函数 f (t)在此时刻的导数.但根据函数 c=f (t)的图象,由导数的几何意义知,函数f(t)在此时刻的导数就是对应点处切线的斜率. 画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此时刻药物浓度瞬时变化率的近似值.解:例题2讲解.并画出曲线求函数 在 处的导数, 例题3讲解解: 在区间 上的平均变化率为:
令 趋于零。知函数 在 处的导数为数。曲线 在 处的切线为 ,如右图当x=x0时,f ?(x0)是一个确定的数.
当x变化时, f ?(x)便是一个函数,称它为f (x)的导函数(简称导数)y=f (x)的导数有时也记作y?导函数的概念小结函数 f (x)在x=x0处的导数 f ?(x0)f ?(x0)几何意义:(2)若 f ?(x0)>0.函数 f (x)在 x=x0附近单调递增.(3)若 f ?(x0)<0.函数 f (x)在 x=x0附近单调递减.(1)函数 在 处的导数 的几何意义是;曲线 在 处的切线的斜率。作业课本第80习题3.1A组题5,6谢谢指导
