探索勾股定理第一节

新八年级上册第一章《勾股定理》学案
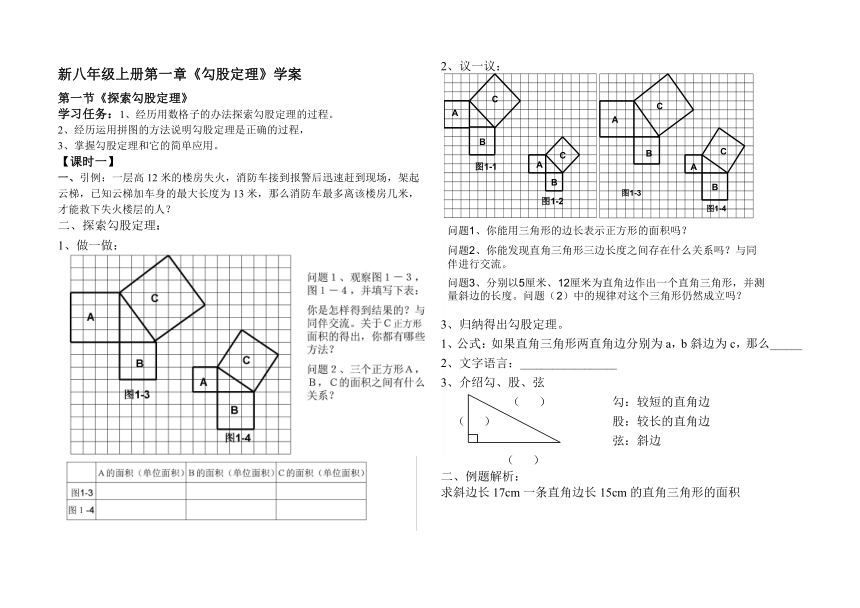
第一节《探索勾股定理》
学习任务：1、经历用数格子的办法探索勾股定理的过程。
2、经历运用拼图的方法说明勾股定理是正确的过程，
3、掌握勾股定理和它的简单应用。
【课时一】
一、引例：一层高12米的楼房失火，消防车接到报警后迅速赶到现场，架起云梯，已知云梯加车身的最大长度为13米，那么消防车最多离该楼房几米，才能救下失火楼层的人？
二、探索勾股定理：
1、做一做：
2、议一议：
3、归纳得出勾股定理。
1、公式：如果直角三角形两直角边分别为a，b斜边为c，那么______
2、文字语言：__________________
3、介绍勾、股、弦
（ ） 勾：较短的直角边
（ ） 股：较长的直角边
弦：斜边
（ ）
二、例题解析：
求斜边长17cm一条直角边长15cm的直角三角形的面积
三、开心一练：
四、拓展延伸：
1、等腰直角三角形的斜边长为2，其面积为
2、在方格纸中，一个小正方形的面积是1，则图中四边形ABCD的面积是
.
3.如图（五），Rt△ABC中，∠ACB=90°，CD⊥AB，若AC=12，BC=5，则CD= .
4.如图（六），工人师傅准备在一个长.宽分别是10cm，9cm的长方形铁板上打两个小孔，小孔的圆心距两边的距离都是3cm，则两孔圆心间的距离是 cm.
【课时二】
一、探索新知：
2002年世界数学家大会在北京召开，这届大会会标的中央图案是经过艺术处理的“弦图”，它既标志着中国古代的数学成就，又像一只转动的风车，欢迎来自世界各地的数学家们！图中大正方形的面积可表示为什么？你有几种表示办法？你能得出什么结论？
二、例题解析：
例1、如图 1．是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c．图 2．是以c为直角边的等腰直角三角形．请你开动脑筋，将它们拼成一个能证明勾股定理的图形．
1．画出拼成的这个图形的示意图，写出它是什么图形？
2．用这个图形证明勾股定理．
3．假设图 1．中的直角三角形有若干个，你能运用图 1．中所给的直角三角形拼成另一种能证明勾股定理的图形吗？请画出拼后的示意图 无需证明．
例2、我方侦查员小王在距离东西向公路400米处侦查，发现一辆敌方汽车在公路上急驶，他赶紧拿出红外测距仪，测得汽车与他相距400米，10秒后，汽车与他相距500米，你能帮助小王计算敌方汽车的速度吗？
三、议一议
（书14页中的图1—15）
观察上图，应用数格子的方法判断图中的三角形的三边长是否满足
注意：勾股定理存在于（ ）三角形中，不是（ ）三角形就不能使用勾股定理。
四、开心一练：
1、在直角三角形中，a，b为直角边，c为斜边.（1）若a=3，b=4，则c= .（2）若c=17，a=15，则b= .
2.小明.小红在同一位置，小明向北走了6m，小红向东走了8m，这时两人相距 m.
3、等腰△ABC中，AB=AC=17cm，BC=16cm，则△ABC的面积是
4. 一根旗杆在离地面9 m处断裂，旗杆顶部落在离旗杆底部12 m的地面上，旗杆在折断之前高度为 。
5、在四边形ABCD中，∠BAD =，∠DBC =，AD = 3，AB = 4，BC = 12，求CD；
五、拓展延伸：
铁路上A，B两点相距25km，C，D为两村庄，DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等，则E站应建在离A站多少km处？
a
b
c
a
b
c
c
c
（1）
（2）
C
B
E
D
500
4000
C
B
A
A