探索勾股定理

第一章 勾股定理
探索勾股定理（第一课时）
一、学情分析：
学生经历了一年的初中学习，具备了一定的归纳总结、类比、转化以及数学表达的能力，对现实生活中的数学知识充满强烈的好奇心与探究欲，并能在老师的引导下，通过小组成员间的互助合作，开展实践探索活动，发表自己的见解。另外在学本节课时，通过前置知识的学习，学生对直角三角形的三边关系及三角关系已有了初步的认识，并能从直观上把握直角三角形的一些特征，为此授课过程中要抓住学生的这些特点，激发学生学习数学的兴趣，建立他们的自信心，为学生空间观念的发展、数学活动经验的积累、个性的发挥提供机会。
2、 教材分析：
（一）本节内容分析：
本节课是八年级开始的第一节课，是学好勾股定理这一章的基础。根据课程标准的要求，要注意让学生经历探索勾股定理的过程，鼓励学生用不同的方法解决，在解决过程中注意渗透数形结合思想。另外勾股定理是刻画直角三角形三边数量关系的定理，也是反映自然界基本规律的一条非常重要的结论，所以授课中要尽可能地体现它的文化价值，提高学生探索的欲望。
（二）教学目标：
1、经历探索勾股定理的过程，提高学生的推理能力，体会数形结合的思想。
2、理解并掌握勾股定理，能利用勾股定理解决一些实际问题。
3、通过对勾股定理的历史介绍及交流，让学生体会它的文化价值，提高学习数学的兴趣和信心。
（三）教学重点难点
1、充分体现探索过程，让学生主动探索交流。
2、直观得出勾股定理，并用自己的语言进行描述。
3、掌握勾股定理。
三、总体设计思路：
为完成上述目标，本节课在设计思路上采用“问题情景 ——问题解决——归纳总结——巩固练习——应用拓展——回顾思考”的六段式教学模式展开教学。
本节课通过阅读章前图所配文字及介绍勾股定理的历史引入新课，让学生认识所要解决的问题。在利用方格纸探索勾股定理的过程中让学生进行思考、讨论、交流，经过学生的观察、归纳、猜想，发现问题并鼓励学生运用自己的语言进行表达。通过练习加深学生对勾股定理认识的同时，提出勾股定理与现实生活的联系，让学生感受数学的应用价值。最后师生共同回顾总结，找出本节课的困惑，加以指导。
四、教学方法：
1、本节课采用“感知归纳法”，利用多媒体课件呈现丰富的问题情景，采用自主探究、合作交流的学习方式。教师适时引导、点拨，协助归纳总结。
2、对于运用勾股定理解决实际问题，要使学生整体把握和分析哪是直角边，哪是斜边，并引导学生总结运用勾股定理解决实际问题的过程，善于发掘学生的新见解，并及时给予肯定，捕捉学生思维中的亮点，鼓励和促进学生进行创造性思维。
五、学法指导：
为了更好地认识勾股定理，发展推理能力，教科书中设计了让同学们自己探索勾股定理的过程，即通过数方格计算面积的方法发现勾股定理，在学习中应鼓励学生认真地数一数，试一试，体会数形结合的思想。
六、教学过程：
（一）创设情境，引入新课：
1、阅读章前图：教师带领学生阅读章前图所配文字，激发学生的学习兴趣和求 知欲。让我们一起走进神秘而有趣的勾股定理世界吧!
2、尽可能地介绍勾股定理的历史，体现其文化价值。
如：我国是最早了解勾股定理的国家之一。在四千多年前，我国人民就应用了这条定理；古巴比伦人在三千多年前也了解了勾股定理；两千年前，古希腊的毕达哥拉斯学派首先验证了这个定理，希腊人把它称为毕达哥拉斯定理；古埃及人与印度人也了解了这一关系并由此得到了直角。当考虑等腰直角三角形的斜边时，这一定理又导致了无理数的产生——数学历史上的第一次危机。
鼓励学生自己从书籍、网络上查阅资料，了解更多的有关勾股定理的内容，体会它的文化价值。
[设计意图]：达到激趣导学的目的。
（二）探索勾股定理
1、投影课本P2引例。
提出本题的主要问题，让学生进行思考、讨论、交流，经过观察、归纳、猜想，发现图1-1中的三个正方形A，B，C的面积之间的关系。通过图1-1的关系，猜想图1-2中三个正方形面积之间的关系，也可利用观察，数方格的方法得到这一关系。
[设计意图]：问题的设置符合学生的认知特点，学生易于接受，对于图1-2中三个正方形面积之间的关系，先猜想后数方格，使学生的思维由直觉思维——抽象思维——直觉思维，另外在学生自主探究的过程中，鼓励学生运用自己的语言进行表达和交流。
[设计预想]：学生在填空的过程中，利用数方格的方法很容易得出正方形A，B的面积，对于正方形C的面积，个别学生可能有一定难度，要适时地组织学生讨论，交流。学生可能采用不同的“割补”方法数，只要合理，就给予鼓励。
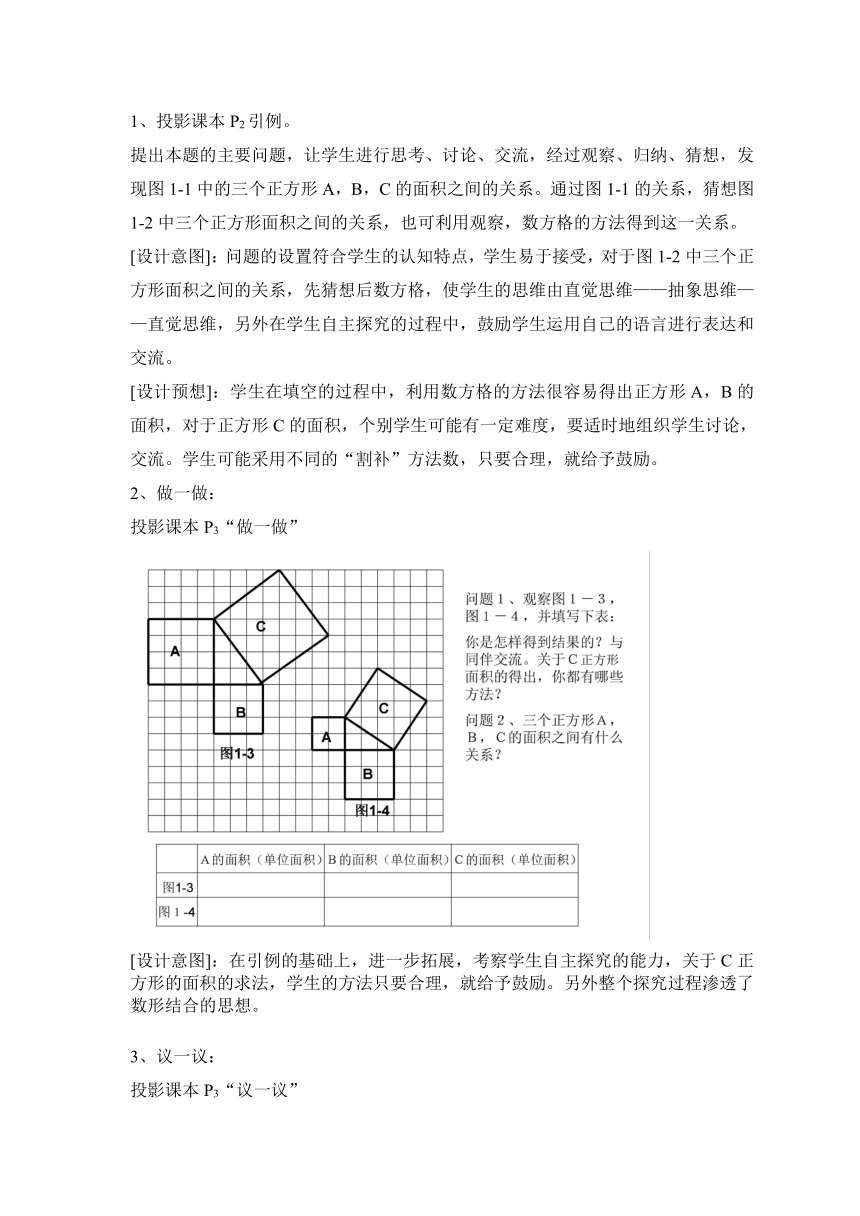
2、做一做：
投影课本P3“做一做”
[设计意图]：在引例的基础上，进一步拓展，考察学生自主探究的能力，关于C正方形的面积的求法，学生的方法只要合理，就给予鼓励。另外整个探究过程渗透了数形结合的思想。
3、议一议：
投影课本P3“议一议”
[设计意图]：1、问题1的目的让学生将正方形的面积与三角形的边长联系起来，为问题2的思考奠定了基础。
2、问题3目的是，在问题2的基础上，再考察一个特例，以使学生确认自己的发现，但在测量中，教师可提醒学生注意测量的误差。如果时间可以的话，可让学生任意画一个直角三角形，再次验证自己的发现。
(三)归纳得出勾股定理。
1、公式：如果直角三角形两直角边分别为a，b斜边为c，那么a2+b2=c2
2、文字语言：直角三角形两直角边的平方和等于斜边的平方。
3、介绍勾、股、弦
弦 勾：较短的直角边
勾 股：较长的直角边
弦：斜边
股
[设计意图]：水到渠成，将学生的观察，探索，感知上升为规范的数学理论，学生的表述不一定全面，规范，但教师应鼓励学生用自己的语言阐述发现的结论。
（四）开心一练
[设计思路]：1、第一题是对学生是否参与整个探究过程的考验，又让学生体会到勾股定理与正方形面积之间的联系。可适当地问一下为什么。
2、第二题是勾股定理的直接应用问题，学生有了数方格的经历，所以不难完成，从中又考察了学生的观察能力。
3、第三题是最常见的考察勾股定理的模式，但学生可能在语言表述的严谨性，书写的规范性方面出现问题，为此教师不妨板书一题。如：图2由勾股定理得：x2+62=102所以x2=64则x=8，使学生在书写作业时有的放矢。
4、第四、第五题是两个勾股定理的实际应用问题，考察学生能否应用所学知识解决实际问题，此外对学生的阅读理解能力也是一个很好的考察。
5、关于想一想，这是一个有趣的实际问题，用以验证勾股定理，提高学生的学习兴趣。
（五）课堂小结：
通过本节课的学习，你有什么收获、感悟或者困惑？
（六）布置作业
课本第6页习题1.1第1、2、3、4题
七、教学反思：
1、为学生设计了自主探索勾股定理内容以及验证它的素材和空间——经历观察、归纳、猜想和验证的数学发展过程。在教育活动中充分发挥了民主，使学生在平等，和谐的气氛中完成数学活动。
2、注重学生提出的问题并认真对待，不是回避，也不是敷衍了事，充分注重“学生的问题是教学的亮点”，这在无形中给学生提供一个广袤的思想空间，正如一个学生所说“给我一点阳光，我会更灿烂”。但如何培养大多数学生提问题的能力与勇气这仍待我不断地探索。