2010年中考数学专题复习动态问题解析
文档属性
| 名称 | 2010年中考数学专题复习动态问题解析 |

|
|
| 格式 | rar | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-24 13:01:00 | ||
图片预览


文档简介
课件27张PPT。2010年中考数学专题复习
动态问题解析1.如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP的长为半径的圆的面积S与点P的运动时间t之间的函数图象大致为( )一.选择题A2.如图,在方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A.先向下平移3格,再向右平移1格
B.先向下平移2格,再向右平移1格
C.先向下平移2格,再向右平移2格
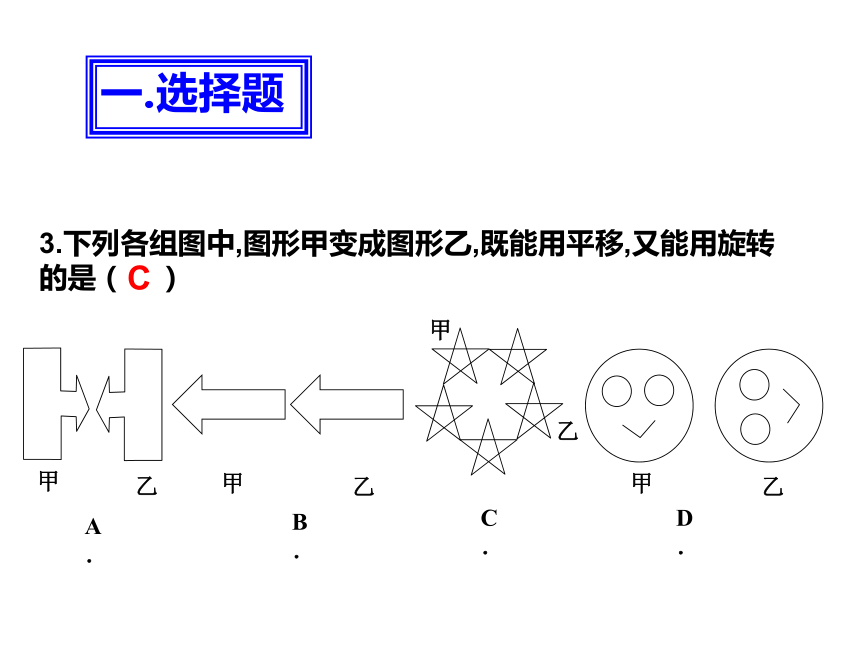
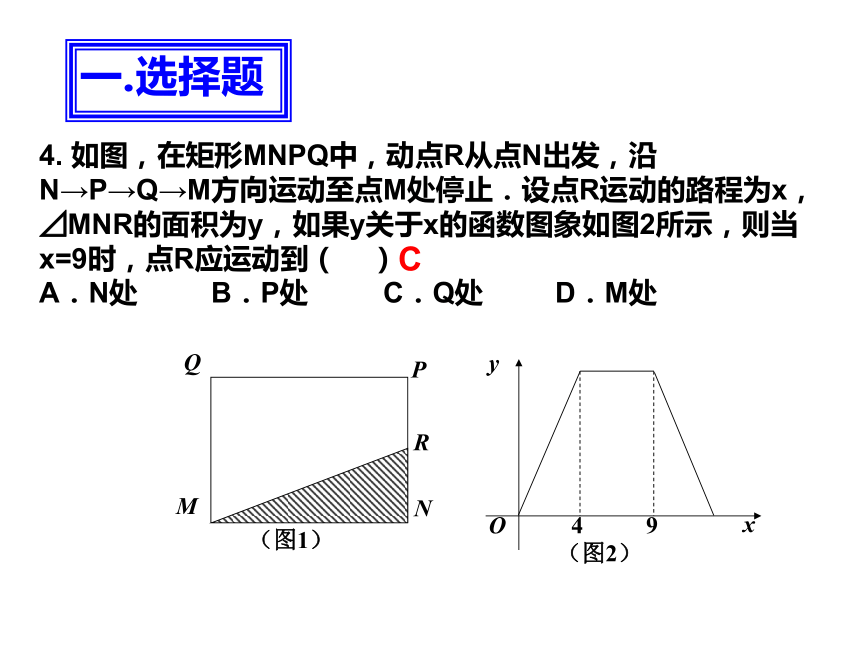
D.先向下平移3格,再向右平移2格一.选择题D3.下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是( )一.选择题C4. 如图,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,⊿MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
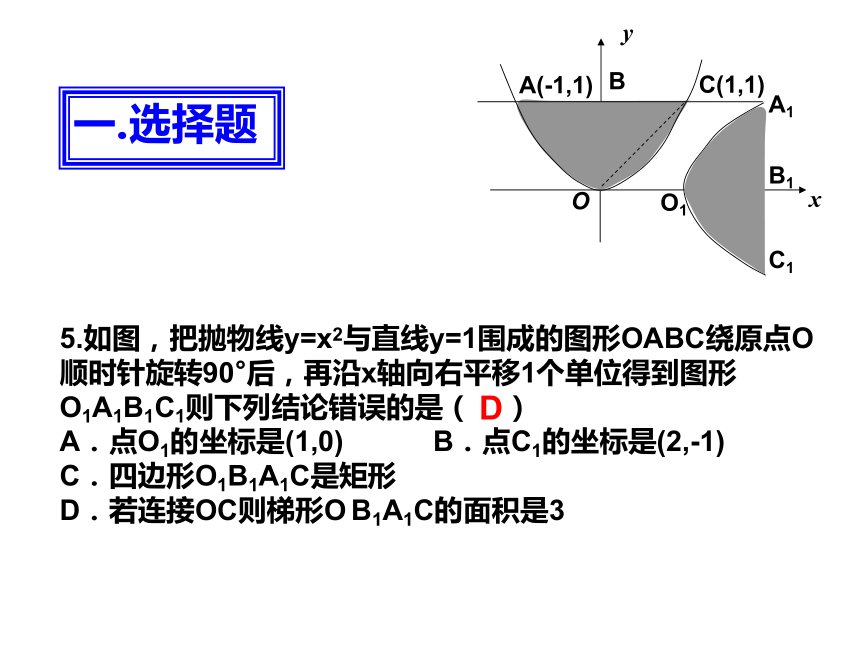
A.N处 B.P处 C.Q处 D.M处一.选择题C5.如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1则下列结论错误的是( )
A.点O1的坐标是(1,0) B.点C1的坐标是(2,-1)
C.四边形O1B1A1C是矩形
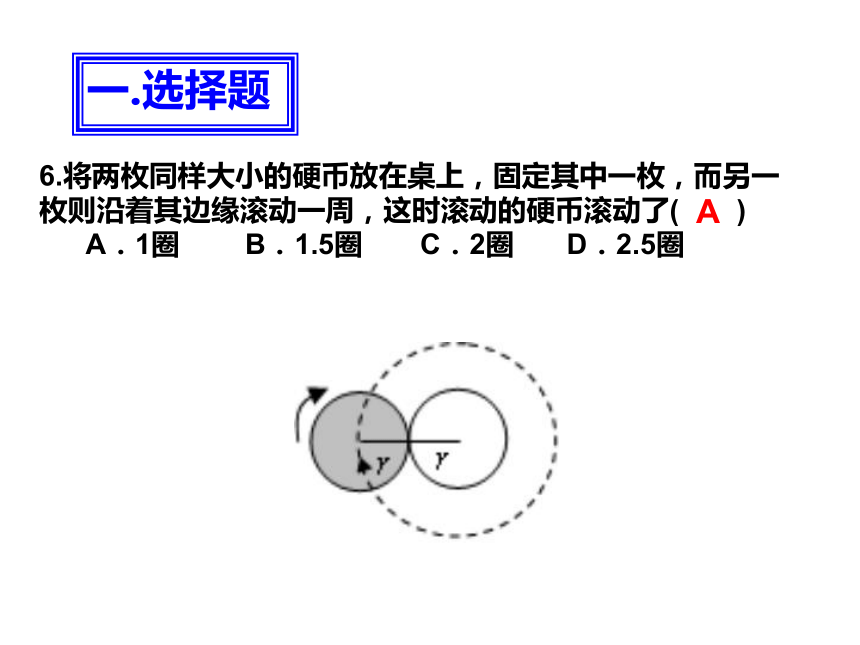
D.若连接OC则梯形O B1A1C的面积是3一.选择题D6.将两枚同样大小的硬币放在桌上,固定其中一枚,而另一枚则沿着其边缘滚动一周,这时滚动的硬币滚动了( )
A.1圈 B.1.5圈 C.2圈 D.2.5圈一.选择题A7.如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是______cm.二.填空题8.如图,已知⊿ACB与⊿DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的⊿ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC
交DE于点G,则线段FG的长为 cm(保留根号).二.填空题9.在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为
_____㎝(结果不取近似值).二.填空题O10.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,
BC=2,点0是AC的中点,过点0的直线l从与AC重合的位置开始,
绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于
点E,设直线l的旋转角为α.
(1)①当α= 度时,四边形EDBC是
等腰梯形,此时AD的长为 .
②当α= 度时,四边形EDBC是
直角梯形,此时AD的长为 .
(2)当α=90°时,判断四边形EDBC
是否为菱形,并说明理由.二.填空题30°60°13/2ED当α=90°时,四边形EDBC是菱形.∵当α=90°时,ED∥BC,
∠COE=∠ACB=α=90°,
∠E=∠ADO=∠B=60°,∴BD=DE=CE=BC=2,则四边形EDBC是菱形.11.已知⊿ABC为直角三角形,∠ACB=90°,AC=AB,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点
B之间的一动点,连结PQ并延长
交BC于点E,连结 BQ并延长交
AC于点F,试证明:FC(AC+EC)
为定值.三.解答题11.已知⊿ABC为直角三角形,∠ACB=90°,AC=AB,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;(3)设点Q为抛物线上点P至点
B之间的一动点,连结PQ并延长
交BC于点E,连结 BQ并延长交
AC于点F,试证明:FC(AC+EC)
为定值.12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式.
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速
度沿OC和BO运动,当其中一个点停止
运动时另一个点也随之停止运动.设它
们的运动的时间为t(s),连接PQ,当t为
何值时,四边形BCPQ的面积最小?并
求出最小值及此时PQ的长. 三.解答题12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式.12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速
度沿OC和BO运动,当其中一个点停止
运动时另一个点也随之停止运动.设它
们的运动的时间为t(s),连接PQ,当t为
何值时,四边形BCPQ的面积最小?并
求出最小值及此时PQ的长. 17.如图,二次函数()的图象与x轴交于A,B两点,与y轴相交于点C.连结AC、BC,A、C两点的坐标分别为A(-3,0)、C(0, ),且当和时二次函数的函数值相等.
(1)求实数的值;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t秒时,连结MN,将⊿BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;
(3)在(2)的条件下,二次函数图象
的对称轴上是否存在点Q,使得以
B,N,Q为项点的三角形与⊿ABC
相似?如果存在,请求出点Q的坐
标;如果不存在,请说明理由.三.解答题18.如图,在梯形ABCD中,AD∥BC,AD=2BC=4,点M是AD的中点,⊿MBC是等边三角形.
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y求y与x的函数关系式;
(3)在(2)中:①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的
四边形是平行四边形?并指出
符合条件的平行四边形的个数;
②当取最小值时,判断⊿PQC的
形状,并说明理由.三.解答题三.解答题19.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线
于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,
判断有几个时刻使得△CEQ是等腰
三角形?请直接写出相应的t值.三.解答题20.如图1、图2,是一款家用的垃圾桶,踏板AB(与地面平行)或绕定点P(固定在垃圾桶底部的某一位置)上下转动(转动过程中始终保持AP=A′P,BP=B′P).通过向下踩踏点A到A′(与地面接触点)使点B上升到点B′,与此同时传动杆BH运动到B′H′的位置,点H绕固定点D旋转(DH为旋转半径)至点H′,从而使桶盖打开一个张角∠HDH′.如图3,桶盖打开后,传动杆H′B′所在的直线分别与水平直线AB、DH垂直,垂足为点M、C,设H′C=B′M.测得AP=6cm,PB=12cm,DH′=8cm. 要使桶盖张开的角度∠HDH′不小于60°,那么踏板AB离地面的高度至少等于多少cm?(结果保留两位有效数字)(参考数据:≈1.41,≈1.73)三.解答题21.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求直线AC的解析式;
(2)连BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.三.解答题22.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt⊿ABM∽Rt⊿MCN.
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式.当M点运动到什么位置时,四边形ABCN面积最大,并求出最大面积;
(3)当点运动到什么位置时Rt⊿ABM∽Rt⊿AMN,求x的值.三.解答题23.如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,
当点P沿A→B→C→D匀速运动
时,OP与PQ能否相等,若能,写出
所有符合条件的t的值;若不能,请
说明理由.三.解答题24.如图,直线的解析式为y=-x+4,它与x轴、y轴分别相交于A、B两点.平行于直线的直线m从原点O出发,沿x轴的正方形以每秒1个单位长度的速度运动,它与x轴、y轴分别相交于M、N两点,设运动时间为t秒(0<t≤4).
(1)求A、B两点的坐标;
(2)用含t的代数式表示⊿MON的面积S1.
(3)以MN为对角线作矩形OMPN,记⊿MPN和⊿OAB重合部分的面积为S2.
①当2<t≤4时,试探究
S1与t之间的函数关系式;
②在直线m的运动过程
中,当t为何值时,S2为
⊿OAB面积的?三.解答题25.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45o,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)三.解答题26.如图,已知直线与轴交于点A,与轴交于点D,抛物线与直线交于A、E两点,与轴交于B、C两点,且B点坐标为 (1,0).⑴求该抛物线的解析式;
⑵动点P在轴上移动,当△PAE是直角三角形时,求点P的坐标P.
⑶在抛物线的对称轴上找一点M,使︱AM-MC︱的值最大,求出点M的坐标.
动态问题解析1.如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP的长为半径的圆的面积S与点P的运动时间t之间的函数图象大致为( )一.选择题A2.如图,在方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A.先向下平移3格,再向右平移1格
B.先向下平移2格,再向右平移1格
C.先向下平移2格,再向右平移2格
D.先向下平移3格,再向右平移2格一.选择题D3.下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是( )一.选择题C4. 如图,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,⊿MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
A.N处 B.P处 C.Q处 D.M处一.选择题C5.如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1则下列结论错误的是( )
A.点O1的坐标是(1,0) B.点C1的坐标是(2,-1)
C.四边形O1B1A1C是矩形
D.若连接OC则梯形O B1A1C的面积是3一.选择题D6.将两枚同样大小的硬币放在桌上,固定其中一枚,而另一枚则沿着其边缘滚动一周,这时滚动的硬币滚动了( )
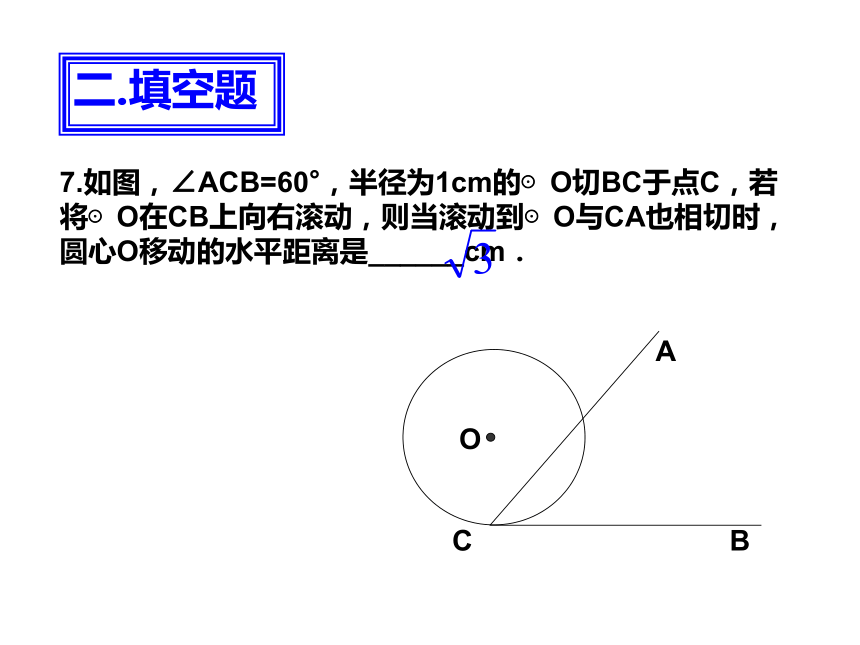
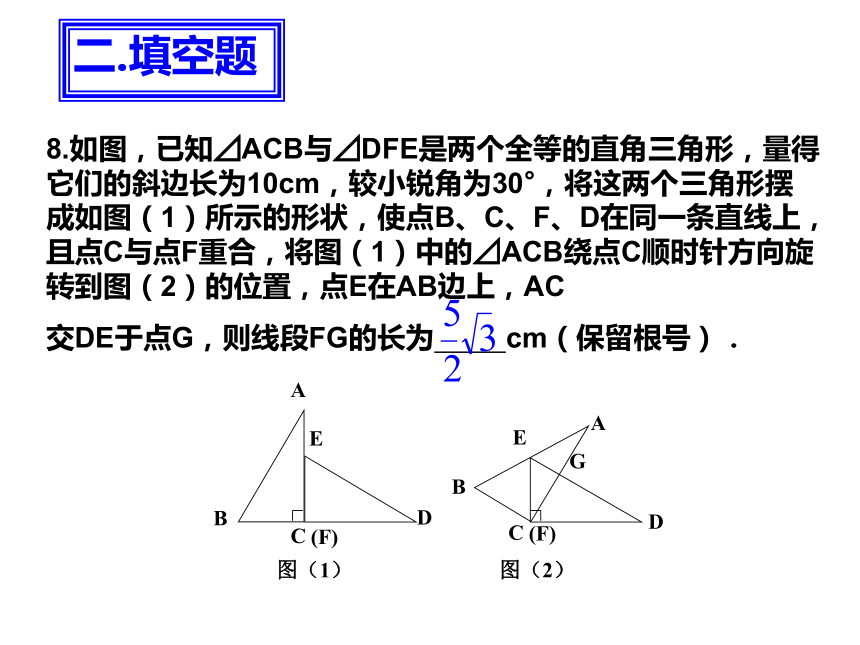
A.1圈 B.1.5圈 C.2圈 D.2.5圈一.选择题A7.如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是______cm.二.填空题8.如图,已知⊿ACB与⊿DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的⊿ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC
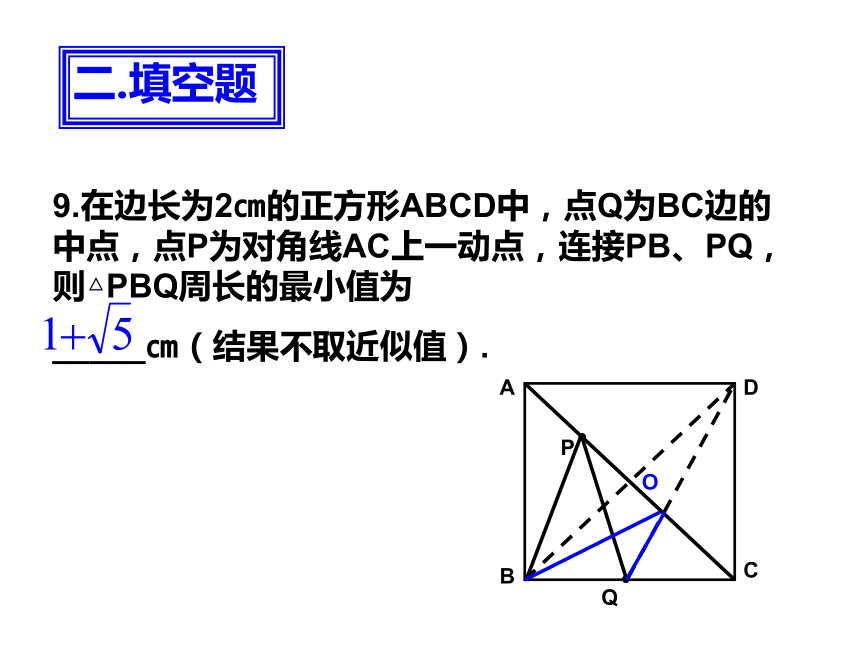
交DE于点G,则线段FG的长为 cm(保留根号).二.填空题9.在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为
_____㎝(结果不取近似值).二.填空题O10.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,
BC=2,点0是AC的中点,过点0的直线l从与AC重合的位置开始,
绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于
点E,设直线l的旋转角为α.
(1)①当α= 度时,四边形EDBC是
等腰梯形,此时AD的长为 .
②当α= 度时,四边形EDBC是
直角梯形,此时AD的长为 .
(2)当α=90°时,判断四边形EDBC
是否为菱形,并说明理由.二.填空题30°60°13/2ED当α=90°时,四边形EDBC是菱形.∵当α=90°时,ED∥BC,
∠COE=∠ACB=α=90°,
∠E=∠ADO=∠B=60°,∴BD=DE=CE=BC=2,则四边形EDBC是菱形.11.已知⊿ABC为直角三角形,∠ACB=90°,AC=AB,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点
B之间的一动点,连结PQ并延长
交BC于点E,连结 BQ并延长交
AC于点F,试证明:FC(AC+EC)
为定值.三.解答题11.已知⊿ABC为直角三角形,∠ACB=90°,AC=AB,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;(3)设点Q为抛物线上点P至点
B之间的一动点,连结PQ并延长
交BC于点E,连结 BQ并延长交
AC于点F,试证明:FC(AC+EC)
为定值.12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式.
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速
度沿OC和BO运动,当其中一个点停止
运动时另一个点也随之停止运动.设它
们的运动的时间为t(s),连接PQ,当t为
何值时,四边形BCPQ的面积最小?并
求出最小值及此时PQ的长. 三.解答题12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式.12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?12.如图,已知抛物线y=a(x-1)2+3(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速
度沿OC和BO运动,当其中一个点停止
运动时另一个点也随之停止运动.设它
们的运动的时间为t(s),连接PQ,当t为
何值时,四边形BCPQ的面积最小?并
求出最小值及此时PQ的长. 17.如图,二次函数()的图象与x轴交于A,B两点,与y轴相交于点C.连结AC、BC,A、C两点的坐标分别为A(-3,0)、C(0, ),且当和时二次函数的函数值相等.
(1)求实数的值;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t秒时,连结MN,将⊿BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;
(3)在(2)的条件下,二次函数图象
的对称轴上是否存在点Q,使得以
B,N,Q为项点的三角形与⊿ABC
相似?如果存在,请求出点Q的坐
标;如果不存在,请说明理由.三.解答题18.如图,在梯形ABCD中,AD∥BC,AD=2BC=4,点M是AD的中点,⊿MBC是等边三角形.
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y求y与x的函数关系式;
(3)在(2)中:①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的
四边形是平行四边形?并指出
符合条件的平行四边形的个数;
②当取最小值时,判断⊿PQC的
形状,并说明理由.三.解答题三.解答题19.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线
于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,
判断有几个时刻使得△CEQ是等腰
三角形?请直接写出相应的t值.三.解答题20.如图1、图2,是一款家用的垃圾桶,踏板AB(与地面平行)或绕定点P(固定在垃圾桶底部的某一位置)上下转动(转动过程中始终保持AP=A′P,BP=B′P).通过向下踩踏点A到A′(与地面接触点)使点B上升到点B′,与此同时传动杆BH运动到B′H′的位置,点H绕固定点D旋转(DH为旋转半径)至点H′,从而使桶盖打开一个张角∠HDH′.如图3,桶盖打开后,传动杆H′B′所在的直线分别与水平直线AB、DH垂直,垂足为点M、C,设H′C=B′M.测得AP=6cm,PB=12cm,DH′=8cm. 要使桶盖张开的角度∠HDH′不小于60°,那么踏板AB离地面的高度至少等于多少cm?(结果保留两位有效数字)(参考数据:≈1.41,≈1.73)三.解答题21.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求直线AC的解析式;
(2)连BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.三.解答题22.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt⊿ABM∽Rt⊿MCN.
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式.当M点运动到什么位置时,四边形ABCN面积最大,并求出最大面积;
(3)当点运动到什么位置时Rt⊿ABM∽Rt⊿AMN,求x的值.三.解答题23.如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,
当点P沿A→B→C→D匀速运动
时,OP与PQ能否相等,若能,写出
所有符合条件的t的值;若不能,请
说明理由.三.解答题24.如图,直线的解析式为y=-x+4,它与x轴、y轴分别相交于A、B两点.平行于直线的直线m从原点O出发,沿x轴的正方形以每秒1个单位长度的速度运动,它与x轴、y轴分别相交于M、N两点,设运动时间为t秒(0<t≤4).
(1)求A、B两点的坐标;
(2)用含t的代数式表示⊿MON的面积S1.
(3)以MN为对角线作矩形OMPN,记⊿MPN和⊿OAB重合部分的面积为S2.
①当2<t≤4时,试探究
S1与t之间的函数关系式;
②在直线m的运动过程
中,当t为何值时,S2为
⊿OAB面积的?三.解答题25.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45o,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)三.解答题26.如图,已知直线与轴交于点A,与轴交于点D,抛物线与直线交于A、E两点,与轴交于B、C两点,且B点坐标为 (1,0).⑴求该抛物线的解析式;
⑵动点P在轴上移动,当△PAE是直角三角形时,求点P的坐标P.
⑶在抛物线的对称轴上找一点M,使︱AM-MC︱的值最大,求出点M的坐标.
同课章节目录
