1.3.1函数的单调性和最值讲义
文档属性
| 名称 | 1.3.1函数的单调性和最值讲义 |  | |
| 格式 | rar | ||
| 文件大小 | 64.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-25 21:11:00 | ||
图片预览

文档简介
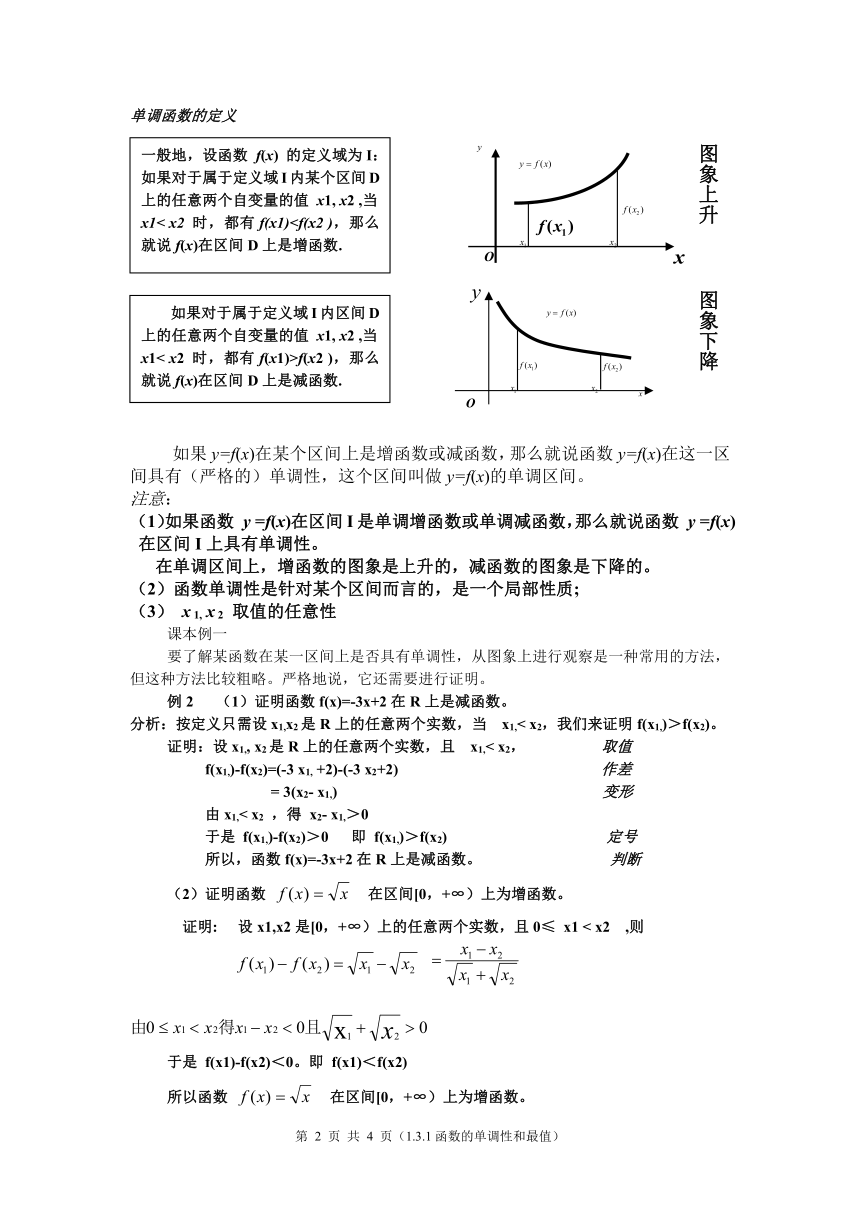
观察以下各个函数图象,体会它们的特点:
单调函数的定义
如果y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这个区间叫做y=f(x)的单调区间。
注意:
(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。
(2)函数单调性是针对某个区间而言的,是一个局部性质;
(3) x 1, x 2 取值的任意性
课本例一
要了解某函数在某一区间上是否具有单调性,从图象上进行观察是一种常用的方法,但这种方法比较粗略。严格地说,它还需要进行证明。
例2 (1)证明函数f(x)=-3x+2在R上是减函数。
分析:按定义只需设x1,x2是R上的任意两个实数,当 x1,< x2,我们来证明f(x1,)>f(x2)。
证明:设x1,, x2是R上的任意两个实数,且 x1,< x2, 取值
f(x1,)-f(x2)=(-3 x1, +2)-(-3 x2+2) 作差
= 3(x2- x1,) 变形
由x1,< x2 ,得 x2- x1,>0
于是 f(x1,)-f(x2)>0 即 f(x1,)>f(x2) 定号
所以,函数f(x)=-3x+2在R上是减函数。 判断
(2)证明函数 在区间[0,+∞)上为增函数。
证明: 设x1,x2是[0,+∞)上的任意两个实数,且0≤ x1 < x2 ,则
于是 f(x1)-f(x2)<0。即 f(x1)<f(x2)
所以函数 在区间[0,+∞)上为增函数。
课本例二
例3:写出f(x)=x2-4x+5的单调递增区间,并证明。
解:由f(x)=x2-4x+5=(x-2)2+1
可知f(x)=x2-4x+5的单调递增区间为[2, +∞)
证明:
由2≤x1所以f(x)=x2-4x+5的单调递增区间为[2, +∞)
说明:通过观察函数图象,对函数是否具有某种性质作出一种猜想,然后通过推理的方法,证明这种猜想的正确性。这是发现问题和解决问题的一种常用数学方法。即先猜后证。
练习:
1:求证函数 y=x3在R上是增函数.
2:写出f(x)=x2-4x+5的单调递减区间,并证明。
4、已知函数y=x2-2x+3在区间(-∞,a]上单调递减,则a的取值范围是__.
5、若定义在R上的单调减函数 满足
你知道a的取值范围吗?
最大最小值的意义
最大值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都
有 f(x)≤M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最大值.
仿照上述定义,你能给出函数y=f(x)的最小值的定义吗
最小值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都有 f(x) ≥ M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最小值.
对于函数单调性的定义的理解,要注意以下三点:
(1)单调性是与“区间”紧密相关的概念.一个函数在不同的区间上可以有不同的单调性.
(2)单调性是函数在某一区间上的“整体”性质.因此,定义中的x1, x2 具有任意性,不能用特殊值代替.
(3)由于定义都是充要性命题,因此由 是增(减)函数,
且 ,这说明单调性使得自变量间的不等关系和函数值之间的不等关系可以“正逆互推”。
O
一般地,设函数 f(x) 的定义域为I: 如果对于属于定义域I内某个区间D上的任意两个自变量的值 x1, x2 ,当x1< x2 时,都有f(x1)如果对于属于定义域I内区间D上的任意两个自变量的值 x1, x2 ,当x1< x2 时,都有f(x1)>f(x2 ),那么就说f(x)在区间D上是减函数.
O
O
图象上升
图象下降
3.判断函数 在定义域 上的单调性.
第 4 页 共 4 页(1.3.1函数的单调性和最值)
单调函数的定义
如果y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这个区间叫做y=f(x)的单调区间。
注意:
(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。
(2)函数单调性是针对某个区间而言的,是一个局部性质;
(3) x 1, x 2 取值的任意性
课本例一
要了解某函数在某一区间上是否具有单调性,从图象上进行观察是一种常用的方法,但这种方法比较粗略。严格地说,它还需要进行证明。
例2 (1)证明函数f(x)=-3x+2在R上是减函数。
分析:按定义只需设x1,x2是R上的任意两个实数,当 x1,< x2,我们来证明f(x1,)>f(x2)。
证明:设x1,, x2是R上的任意两个实数,且 x1,< x2, 取值
f(x1,)-f(x2)=(-3 x1, +2)-(-3 x2+2) 作差
= 3(x2- x1,) 变形
由x1,< x2 ,得 x2- x1,>0
于是 f(x1,)-f(x2)>0 即 f(x1,)>f(x2) 定号
所以,函数f(x)=-3x+2在R上是减函数。 判断
(2)证明函数 在区间[0,+∞)上为增函数。
证明: 设x1,x2是[0,+∞)上的任意两个实数,且0≤ x1 < x2 ,则
于是 f(x1)-f(x2)<0。即 f(x1)<f(x2)
所以函数 在区间[0,+∞)上为增函数。
课本例二
例3:写出f(x)=x2-4x+5的单调递增区间,并证明。
解:由f(x)=x2-4x+5=(x-2)2+1
可知f(x)=x2-4x+5的单调递增区间为[2, +∞)
证明:
由2≤x1
说明:通过观察函数图象,对函数是否具有某种性质作出一种猜想,然后通过推理的方法,证明这种猜想的正确性。这是发现问题和解决问题的一种常用数学方法。即先猜后证。
练习:
1:求证函数 y=x3在R上是增函数.
2:写出f(x)=x2-4x+5的单调递减区间,并证明。
4、已知函数y=x2-2x+3在区间(-∞,a]上单调递减,则a的取值范围是__.
5、若定义在R上的单调减函数 满足
你知道a的取值范围吗?
最大最小值的意义
最大值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都
有 f(x)≤M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最大值.
仿照上述定义,你能给出函数y=f(x)的最小值的定义吗
最小值定义:
一般地,设函数 y= f(x) 的定义域为I,如果存在实数M满足: (1)对于任意的 x∈I ,都有 f(x) ≥ M ;(2)存在x0 ∈I,使得 f(x0 )=M. 那么,我们称M是函数y= f(x)的最小值.
对于函数单调性的定义的理解,要注意以下三点:
(1)单调性是与“区间”紧密相关的概念.一个函数在不同的区间上可以有不同的单调性.
(2)单调性是函数在某一区间上的“整体”性质.因此,定义中的x1, x2 具有任意性,不能用特殊值代替.
(3)由于定义都是充要性命题,因此由 是增(减)函数,
且 ,这说明单调性使得自变量间的不等关系和函数值之间的不等关系可以“正逆互推”。
O
一般地,设函数 f(x) 的定义域为I: 如果对于属于定义域I内某个区间D上的任意两个自变量的值 x1, x2 ,当x1< x2 时,都有f(x1)
O
O
图象上升
图象下降
3.判断函数 在定义域 上的单调性.
第 4 页 共 4 页(1.3.1函数的单调性和最值)
