一次函数的图象和性质练习

一次函数的图象和性质练习课（1）
一、教学目标
通过对一次函数图像的复习，加深对一次函数的理解。
通过一次函数图像和解析式相互关系的练习和探究，总结规律，加深对性质的理解，并能运用性质解决实际生活中的问题。
重点：数形结合的思想。
难点：根据实际问题得出解析式，然后画出函数图像。
教学过程
复习引入
提问：一次函数的图象都是一些什么图像？引导学生回答：线段、直线、射线或是一串点。
探究新知
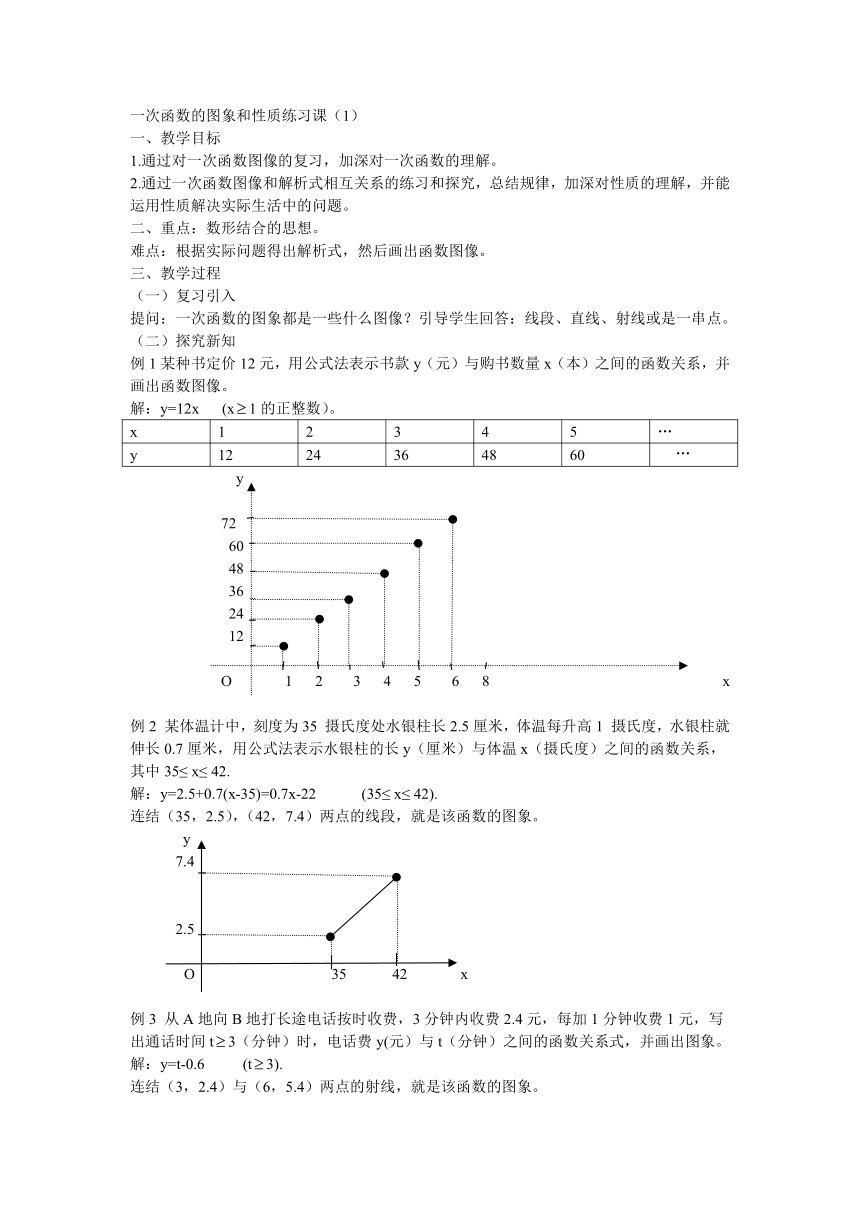
例1某种书定价12元，用公式法表示书款y（元）与购书数量x（本）之间的函数关系，并画出函数图像。
解：y=12x (x1的正整数）。
x 1 2 3 4 5 …
y 12 24 36 48 60 …
y
72
60
48
36
24
12
O 1 2 3 4 5 6 8 x
例2 某体温计中，刻度为35 摄氏度处水银柱长2.5厘米，体温每升高1 摄氏度，水银柱就伸长0.7厘米，用公式法表示水银柱的长y（厘米）与体温x（摄氏度）之间的函数关系，其中35≤ x≤ 42.
解：y=2.5+0.7(x-35)=0.7x-22 (35≤ x≤ 42).
连结（35，2.5），（42，7.4）两点的线段，就是该函数的图象。
y
7.4
2.5
O 35 42 x
例3 从A地向B地打长途电话按时收费，3分钟内收费2.4元，每加1分钟收费1元，写出通话时间t3（分钟）时，电话费y(元）与t（分钟）之间的函数关系式，并画出图象。
解：y=t-0.6 (t3).
连结（3，2.4）与（6，5.4）两点的射线，就是该函数的图象。
y
5.4
2.4
O 1 2 3 4 5 6 x
例4 画出函数y=-2x+3 (1解：
x 1 4
y 1 -5
y
O 1
-1 1 2 3 4 x
-2
-3
-4
-5
例5 画出函数y=-2x+3 的图象。
解：图象过点（0，3），（1，1），连结这两点的直线，就是该函数的图象。
y
3
2
1
1 x
O y=-2x+3
从上面的几个例子可以看出，对于直线、射线、线段，可以用两点法来画，但对于一串点，能不能用两点法来画？待学生回答后，再做出正确的结论。
课堂小结
总结规律：一次函数的图象与自变量的取值范围有什么关系？
当自变量的取值范围是实数集时是直线；当自变量的取值范围是非区间不等式时是一条射线；当自变量的取值范围是区间不等式时是一条线段；当自变量的取值范围是正整数集、负整数集或正整数集时是一串点。
思维拓展
教科书P60 习题C组第2题
作业布置
已知函数y=-x+2分别作出满足下列条件的图象：
x=0,1,2,3,4,5;
-12≤x≤5;
x2;
x取全体实数；
2.如图，已知直线y=x+3的图象与x、y轴交于A、B两点，直线l经过原点，与线段AB交于点C，把 AOB的面积分为2：1两部分，求直线l的解析式。
点拨：本题有以下两种情形:
l y
Y
B l B
C
O O
x x
A A
(1) (2)