3.2 独立性检验的基本思想及其初步应用
文档属性
| 名称 | 3.2 独立性检验的基本思想及其初步应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-07-29 00:00:00 | ||
图片预览



文档简介
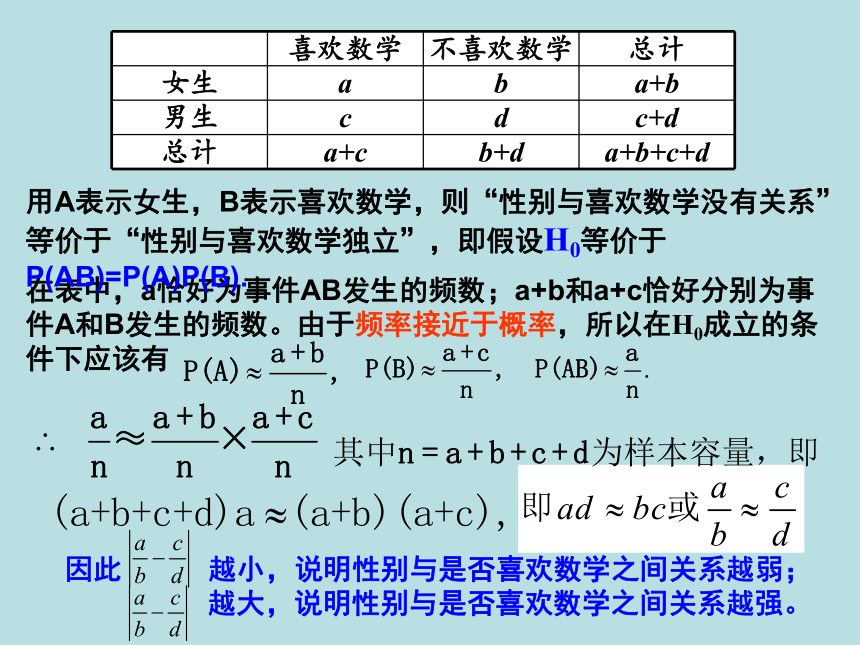
课件11张PPT。3.2独立性检验的基本思想及其初步应用(一) 为了考察性别与是否喜欢数学课程有关系,现在就在我们班做一个调查,得到如下结果(单位:人)互动探究因此 越小,说明性别与是否喜欢数学之间关系越弱;
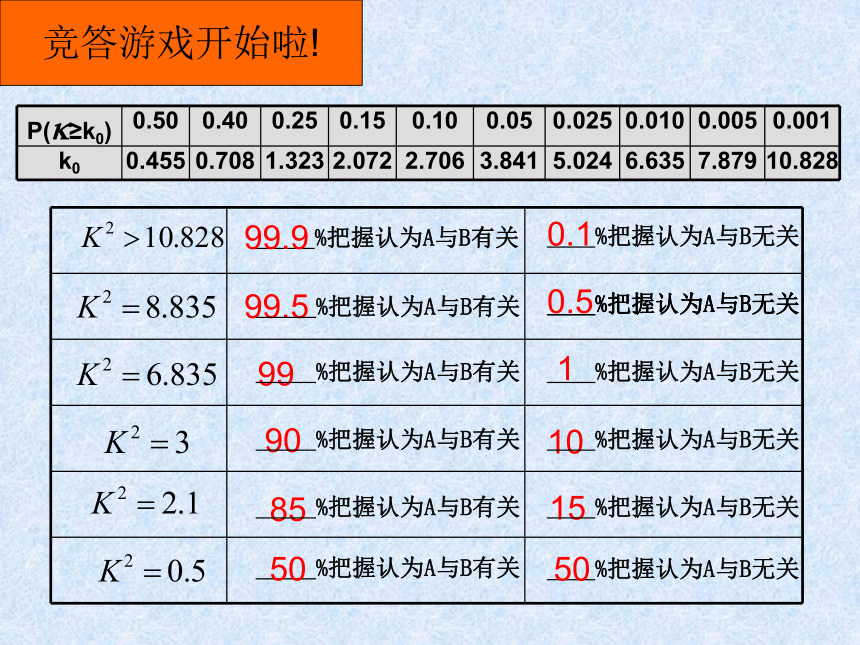
越大,说明性别与是否喜欢数学之间关系越强。在表中,a恰好为事件AB发生的频数;a+b和a+c恰好分别为事件A和B发生的频数。由于频率接近于概率,所以在H0成立的条件下应该有用A表示女生,B表示喜欢数学,则“性别与喜欢数学没有关系”等价于“性别与喜欢数学独立”,即假设H0等价于 P(AB)=P(A)P(B).临界值表独立性检验 为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量-----卡方统计量第一步: H0:性别与喜欢数学课之间没有关系 第二步: 列联表第三步:计算K2的值---观测值k第四步:查临界值表第五步:下结论 %把握认为A与B有关 %把握认为A与B无关99.99999.5 15900.50.110185竞答游戏开始啦! %把握认为A与B有关 %把握认为A与B有关 %把握认为A与B有关 %把握认为A与B有关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B有关 %把握认为A与B无关5050 独立性检验的初步应用第三步:计算第四步:查对临界值表,作出判断。第五步:若出现小概率事件,则拒绝H0;否则接受H0 。独立性检验的定义 上面这种利用随机变量K2来确定在多大程度上可以认为“两个分类变量有关系”的方法,称为两个分类变量的独立性检验。反证法原理与独立性检验原理
在假设H0下,如果推出一个矛盾,就证明了H0不成立.在假设H0 下,如果出现一个与H0相矛盾的小概率事件,就推断H0 不成立,且该推断犯错误的概率不超过这个小概率.PK例1 沅江一个医生随机地调查300个吸烟的人中有285人不患肺癌,而700个不吸烟的人中有693人不患肺癌,请你分析有多大的把握认为“吸烟与患肺癌有关系”。解:第一步:H0: 吸烟和肺癌之间没有关系 第三、四步根据联表中的数据,得到第五步:所以有99.9%的把握认为“吸烟与患肺癌有关系”老师提醒大家:吸烟有害健康哦!第二步:根据题目所给数据得到如下列联表:大于10.8281.在下面2x2列联表中:数值 和 相差越大,则两个变量有关系的可能性就( ) 合作实践2.下面是一个2X2联表:②通过此次调查,你有多大的把握认为“性别与喜欢吃零食有关系”。①计算得到的k值为: 有请生活委员闪亮登场!合作实践课后作业:就本堂课所学的知识分组做一个社会实践调查.
比如:学历与收入是否有关系,性别与是否喜欢运动有关系……分组调查谢谢各位老师指导!
越大,说明性别与是否喜欢数学之间关系越强。在表中,a恰好为事件AB发生的频数;a+b和a+c恰好分别为事件A和B发生的频数。由于频率接近于概率,所以在H0成立的条件下应该有用A表示女生,B表示喜欢数学,则“性别与喜欢数学没有关系”等价于“性别与喜欢数学独立”,即假设H0等价于 P(AB)=P(A)P(B).临界值表独立性检验 为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量-----卡方统计量第一步: H0:性别与喜欢数学课之间没有关系 第二步: 列联表第三步:计算K2的值---观测值k第四步:查临界值表第五步:下结论 %把握认为A与B有关 %把握认为A与B无关99.99999.5 15900.50.110185竞答游戏开始啦! %把握认为A与B有关 %把握认为A与B有关 %把握认为A与B有关 %把握认为A与B有关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B无关 %把握认为A与B有关 %把握认为A与B无关5050 独立性检验的初步应用第三步:计算第四步:查对临界值表,作出判断。第五步:若出现小概率事件,则拒绝H0;否则接受H0 。独立性检验的定义 上面这种利用随机变量K2来确定在多大程度上可以认为“两个分类变量有关系”的方法,称为两个分类变量的独立性检验。反证法原理与独立性检验原理
在假设H0下,如果推出一个矛盾,就证明了H0不成立.在假设H0 下,如果出现一个与H0相矛盾的小概率事件,就推断H0 不成立,且该推断犯错误的概率不超过这个小概率.PK例1 沅江一个医生随机地调查300个吸烟的人中有285人不患肺癌,而700个不吸烟的人中有693人不患肺癌,请你分析有多大的把握认为“吸烟与患肺癌有关系”。解:第一步:H0: 吸烟和肺癌之间没有关系 第三、四步根据联表中的数据,得到第五步:所以有99.9%的把握认为“吸烟与患肺癌有关系”老师提醒大家:吸烟有害健康哦!第二步:根据题目所给数据得到如下列联表:大于10.8281.在下面2x2列联表中:数值 和 相差越大,则两个变量有关系的可能性就( ) 合作实践2.下面是一个2X2联表:②通过此次调查,你有多大的把握认为“性别与喜欢吃零食有关系”。①计算得到的k值为: 有请生活委员闪亮登场!合作实践课后作业:就本堂课所学的知识分组做一个社会实践调查.
比如:学历与收入是否有关系,性别与是否喜欢运动有关系……分组调查谢谢各位老师指导!
