函数的单调性
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
函数的单调性
教学目标
知识目标 理解增函数、减函数的概念;
能力目标 1.掌握判断和证明某些函数增、减性的方法;
2.培养学生观察、比较、分析的能力;
3.增强数形结合的意识与能力;
情感目标 熟悉从感性认识到理性认识,从具体到抽象的研究问题的方法。
教学重点 函数单调性的相关概念
教学难点 证明或判断函数的单调性
教法设想 为了解决难点,提高教学效果。教学过程中力争做到以下几点:
(1)着重注意从实际出发,从感性认识提高到理性认识
(2)注重运用对比的方法和及时利用反馈信息纠错与强化
(3)坚持结合直观图形或函数图象来说明和帮助学生理解概念
(4)充分利用电脑与几何画板等辅助作用,增强教学效果。
教学用具 多媒体、实物投影仪、CAI课件、几何画板软件
教学过程
一.新课引入:
日常生活你知道2008年北京奥运会开幕式时间由原定的7月25日为什么会推迟到8月8日?
通过查阅历史资料可以了解到开幕式推迟主要是天气的原因,北京的天气到8月中旬,平均气温、平均降雨量和平均降雨天数等均开始下降,比较适宜大型国际体育赛事.
下图是北京市今年8月8日一天24小时内气温随时间变化的曲线图.
问题:观察图形,能得到什么信息?
(1)当天的最高温度、最低温度以及何时达到;
(2)在某时刻的温度;
(3)某些时段温度升高,某些时段温度降低.
在生活中,我们关心很多数据的变化规律,了解这些数据的变化规律,对我们的生活是很有帮助的.如水位高低、燃油价格、股票价格等.
用函数观点看,其实就是随着自变量的变化,函数值是变大还是变小.
很多函数也具有类似性质。如:
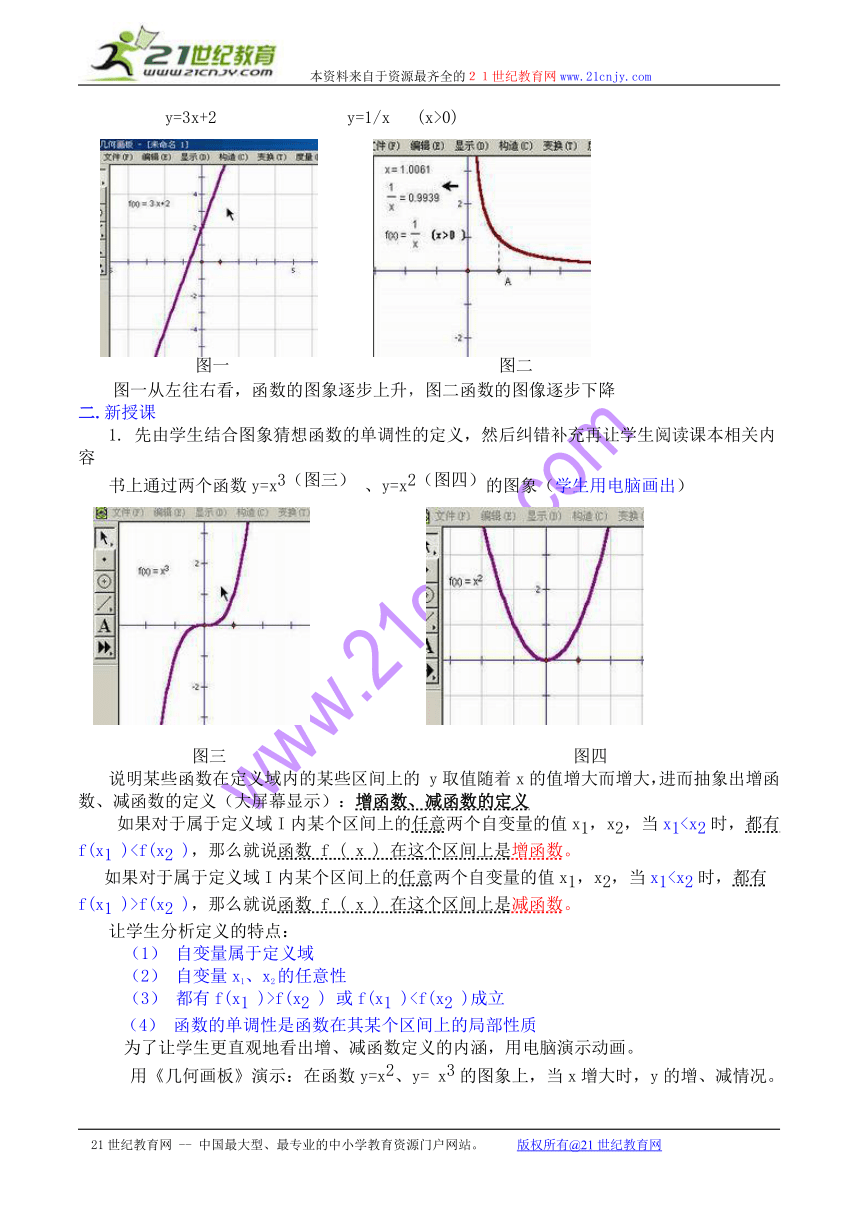
y=3x+2 y=1/x (x>0)
图一 图二
图一从左往右看,函数的图象逐步上升,图二函数的图像逐步下降
二.新授课
1. 先由学生结合图象猜想函数的单调性的定义,然后纠错补充再让学生阅读课本相关内容
书上通过两个函数y=x3(图三) 、y=x2(图四)的图象(学生用电脑画出)
图三 图四
说明某些函数在定义域内的某些区间上的 y取值随着x的值增大而增大,进而抽象出增函数、减函数的定义(大屏幕显示):增函数、减函数的定义
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1f(x2 ),那么就说函数 f ( x ) 在这个区间上是减函数。
让学生分析定义的特点:
(1) 自变量属于定义域
(2) 自变量x1、x2的任意性
(3) 都有f(x1 )>f(x2 ) 或f(x1 )(4) 函数的单调性是函数在其某个区间上的局部性质
为了让学生更直观地看出增、减函数定义的内涵,用电脑演示动画。
用《几何画板》演示:在函数y=x2、y= x3的图象上,当x增大时,y的增、减情况。其中函数其中函数y= x3的图象学生比较陌生,所以当堂用《几何画板》画出,并让学生熟悉用描点法作函数图象的过程。
的图象学生比较陌生,所以当堂用《几何画板》画出,并让学生熟悉用描点法作函数图象的过程。
从上述过程中概括出函数的单调性单调区间的概念:
如果函数在某个区间是增函数或减函数,那么就说函数在这一区间具有(严格的)单调性。这一区间叫做的单调区间。
学生阅读书上例1,回答该函数的单调区间。
思考:该函数在其定义域上有单调性吗?
要了解函数在某些区间上是否具有单调性,从图象上进行观察是一种常用而又较为粗略的方法,严格的说,它需要根据单调函数的定义进行证明。
阅读书上例2、例3,然后与学生一起总结出解题步骤(电脑给出):
(1) 取值
(2) 作差变形(因式分解、配方、有理化等方法)
(3) 定号
(4) 判断
分析各个步骤的含义,利用这个结论学生练习(用电脑给出):
从上述过程中概括出单调性、单调区间的概念:
如果函数y=f(x)在某个区间是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间叫做y=f(x)的单调区间 。
2. 学生阅读课本,回答该函数的单调区间。
思考:该函数在其定义域上有单调性吗?
注意:我们生活中的很多实际问题的函数图象不象函数y=x2、y= x3的图象一样有规律地上升或下降,如我国的人口出生率变化曲线(如下图五,教材P.53),但是我们可以很方便地从图象观察函数在哪个区间是递增或递减,从而确定其单调区间。
图五
要了解函数在某些区间上是否具有单调性,从图象上进行观察是一种常用而又较为粗略的方法,严格的说,它要根据单调函数的定义进行证明。
阅读书上P59. 例2、例3,然后与学生一起总结出(大屏幕显示):
(ⅰ)判断函数单调性的方法:
(1)用图象;(2)用定义;(3)其它(后面会学到)。
(ⅱ)证明函数单调性的方法:目前只能用定义,解题步骤如下
(1) 取值
(2) 作差变形(主要是配方或分解因式等)
(3) 定号
(4) 判断结论
分析各个步骤的含义,利用这个结论,学生练习(电脑给出):
P60练习1、2题
3. 学生分组练习书上习题:
A组 P60.3
B组 P64.4(2)
C组 p65.6(1)
思考题(电脑给出):判断函数f(x) =
在(-,0)(0,+)上的单调性。
(参考右图七)
思考:该函数在其定义域上有单调性吗?
图七
4. 单调性在生活中应用举例:
函数的单调性在生活中应用很广泛,如从前述图五的我国人口出生率曲线,我们可以直观的看到我国人口出生的变化情况;又如股票价格线性图(电脑给出图八:春兰股份线性图),使人对股票价格的涨落情况一目了然。
图八
三.小结:本节课重点要理解函数单调性及相关概念,掌握函数单调性的判断与证明方法与步骤;通过学习,增强数形结合的意识与能力,学会从感性到理性,从具体到抽象的研究问题的方法。
四.作业:书P64习题2.3中,第1、2、3、5题
五.板书设计:
单调性定义单调区间定义 1. 判断函数单调性的方法2. 证明函数单调性的解题步骤(1)(2)(3)(4) 例4的解题过程
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
函数的单调性
教学目标
知识目标 理解增函数、减函数的概念;
能力目标 1.掌握判断和证明某些函数增、减性的方法;
2.培养学生观察、比较、分析的能力;
3.增强数形结合的意识与能力;
情感目标 熟悉从感性认识到理性认识,从具体到抽象的研究问题的方法。
教学重点 函数单调性的相关概念
教学难点 证明或判断函数的单调性
教法设想 为了解决难点,提高教学效果。教学过程中力争做到以下几点:
(1)着重注意从实际出发,从感性认识提高到理性认识
(2)注重运用对比的方法和及时利用反馈信息纠错与强化
(3)坚持结合直观图形或函数图象来说明和帮助学生理解概念
(4)充分利用电脑与几何画板等辅助作用,增强教学效果。
教学用具 多媒体、实物投影仪、CAI课件、几何画板软件
教学过程
一.新课引入:
日常生活你知道2008年北京奥运会开幕式时间由原定的7月25日为什么会推迟到8月8日?
通过查阅历史资料可以了解到开幕式推迟主要是天气的原因,北京的天气到8月中旬,平均气温、平均降雨量和平均降雨天数等均开始下降,比较适宜大型国际体育赛事.
下图是北京市今年8月8日一天24小时内气温随时间变化的曲线图.
问题:观察图形,能得到什么信息?
(1)当天的最高温度、最低温度以及何时达到;
(2)在某时刻的温度;
(3)某些时段温度升高,某些时段温度降低.
在生活中,我们关心很多数据的变化规律,了解这些数据的变化规律,对我们的生活是很有帮助的.如水位高低、燃油价格、股票价格等.
用函数观点看,其实就是随着自变量的变化,函数值是变大还是变小.
很多函数也具有类似性质。如:
y=3x+2 y=1/x (x>0)
图一 图二
图一从左往右看,函数的图象逐步上升,图二函数的图像逐步下降
二.新授课
1. 先由学生结合图象猜想函数的单调性的定义,然后纠错补充再让学生阅读课本相关内容
书上通过两个函数y=x3(图三) 、y=x2(图四)的图象(学生用电脑画出)
图三 图四
说明某些函数在定义域内的某些区间上的 y取值随着x的值增大而增大,进而抽象出增函数、减函数的定义(大屏幕显示):增函数、减函数的定义
如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1
让学生分析定义的特点:
(1) 自变量属于定义域
(2) 自变量x1、x2的任意性
(3) 都有f(x1 )>f(x2 ) 或f(x1 )
为了让学生更直观地看出增、减函数定义的内涵,用电脑演示动画。
用《几何画板》演示:在函数y=x2、y= x3的图象上,当x增大时,y的增、减情况。其中函数其中函数y= x3的图象学生比较陌生,所以当堂用《几何画板》画出,并让学生熟悉用描点法作函数图象的过程。
的图象学生比较陌生,所以当堂用《几何画板》画出,并让学生熟悉用描点法作函数图象的过程。
从上述过程中概括出函数的单调性单调区间的概念:
如果函数在某个区间是增函数或减函数,那么就说函数在这一区间具有(严格的)单调性。这一区间叫做的单调区间。
学生阅读书上例1,回答该函数的单调区间。
思考:该函数在其定义域上有单调性吗?
要了解函数在某些区间上是否具有单调性,从图象上进行观察是一种常用而又较为粗略的方法,严格的说,它需要根据单调函数的定义进行证明。
阅读书上例2、例3,然后与学生一起总结出解题步骤(电脑给出):
(1) 取值
(2) 作差变形(因式分解、配方、有理化等方法)
(3) 定号
(4) 判断
分析各个步骤的含义,利用这个结论学生练习(用电脑给出):
从上述过程中概括出单调性、单调区间的概念:
如果函数y=f(x)在某个区间是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间叫做y=f(x)的单调区间 。
2. 学生阅读课本,回答该函数的单调区间。
思考:该函数在其定义域上有单调性吗?
注意:我们生活中的很多实际问题的函数图象不象函数y=x2、y= x3的图象一样有规律地上升或下降,如我国的人口出生率变化曲线(如下图五,教材P.53),但是我们可以很方便地从图象观察函数在哪个区间是递增或递减,从而确定其单调区间。
图五
要了解函数在某些区间上是否具有单调性,从图象上进行观察是一种常用而又较为粗略的方法,严格的说,它要根据单调函数的定义进行证明。
阅读书上P59. 例2、例3,然后与学生一起总结出(大屏幕显示):
(ⅰ)判断函数单调性的方法:
(1)用图象;(2)用定义;(3)其它(后面会学到)。
(ⅱ)证明函数单调性的方法:目前只能用定义,解题步骤如下
(1) 取值
(2) 作差变形(主要是配方或分解因式等)
(3) 定号
(4) 判断结论
分析各个步骤的含义,利用这个结论,学生练习(电脑给出):
P60练习1、2题
3. 学生分组练习书上习题:
A组 P60.3
B组 P64.4(2)
C组 p65.6(1)
思考题(电脑给出):判断函数f(x) =
在(-,0)(0,+)上的单调性。
(参考右图七)
思考:该函数在其定义域上有单调性吗?
图七
4. 单调性在生活中应用举例:
函数的单调性在生活中应用很广泛,如从前述图五的我国人口出生率曲线,我们可以直观的看到我国人口出生的变化情况;又如股票价格线性图(电脑给出图八:春兰股份线性图),使人对股票价格的涨落情况一目了然。
图八
三.小结:本节课重点要理解函数单调性及相关概念,掌握函数单调性的判断与证明方法与步骤;通过学习,增强数形结合的意识与能力,学会从感性到理性,从具体到抽象的研究问题的方法。
四.作业:书P64习题2.3中,第1、2、3、5题
五.板书设计:
单调性定义单调区间定义 1. 判断函数单调性的方法2. 证明函数单调性的解题步骤(1)(2)(3)(4) 例4的解题过程
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
