1.3.2 函数的奇偶性
图片预览




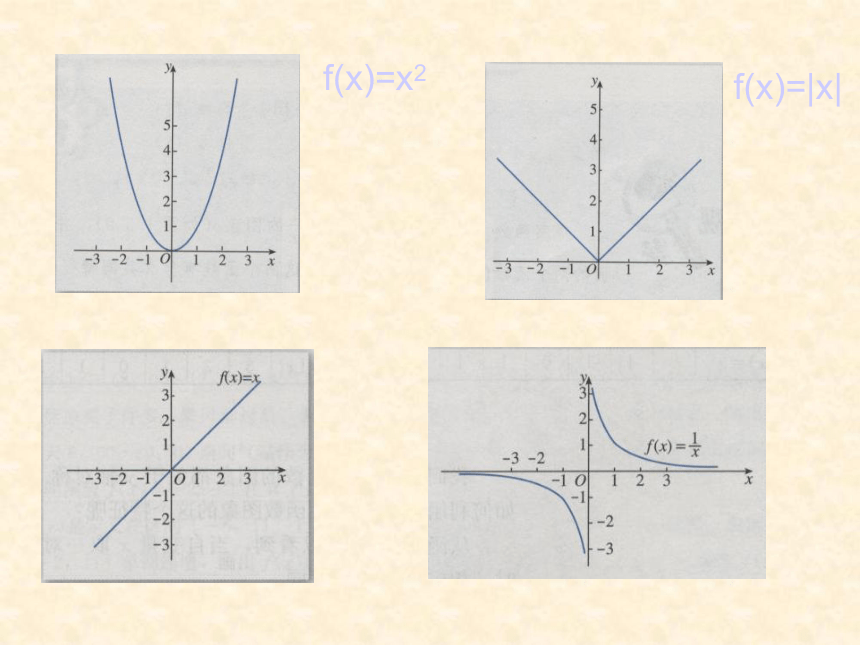


文档简介
课件23张PPT。1.3.2函数的奇偶性 德惠实验中学高一数学组
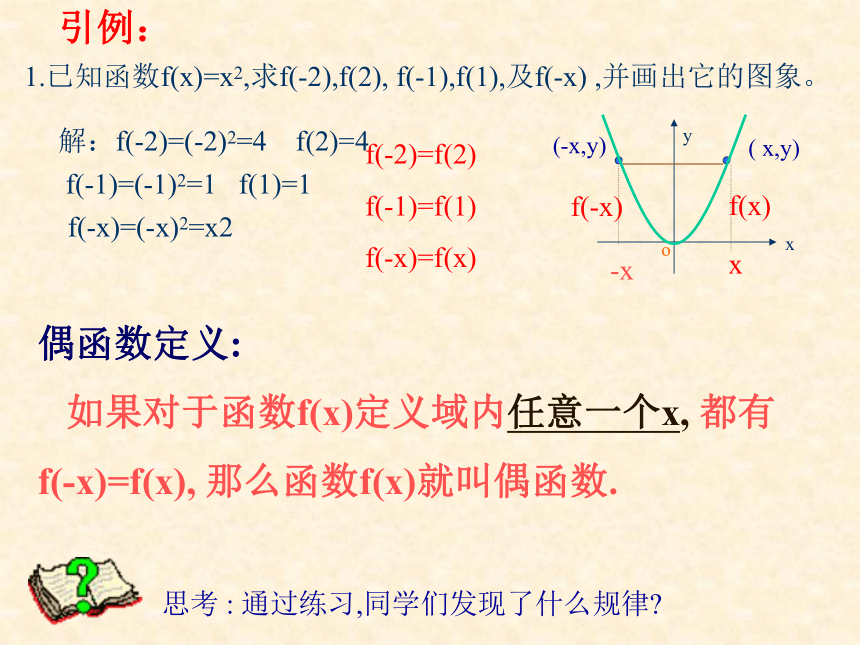
1.3.2函数的奇偶性引例:1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1),及f(-x) ,并画出它的图象。解:f(-2)=(-2)2=4 f(2)=4f(-1)=(-1)2=1 f(1)=1f(-x)=(-x)2=x2-xxf(-x)f(x)f(-2)=f(2)
f(-1)=f(1)
f(-x)=f(x)思考 : 通过练习,同学们发现了什么规律?偶函数定义:
如果对于函数f(x)定义域内任意一个x, 都有
f(-x)=f(x), 那么函数f(x)就叫偶函数.引例:
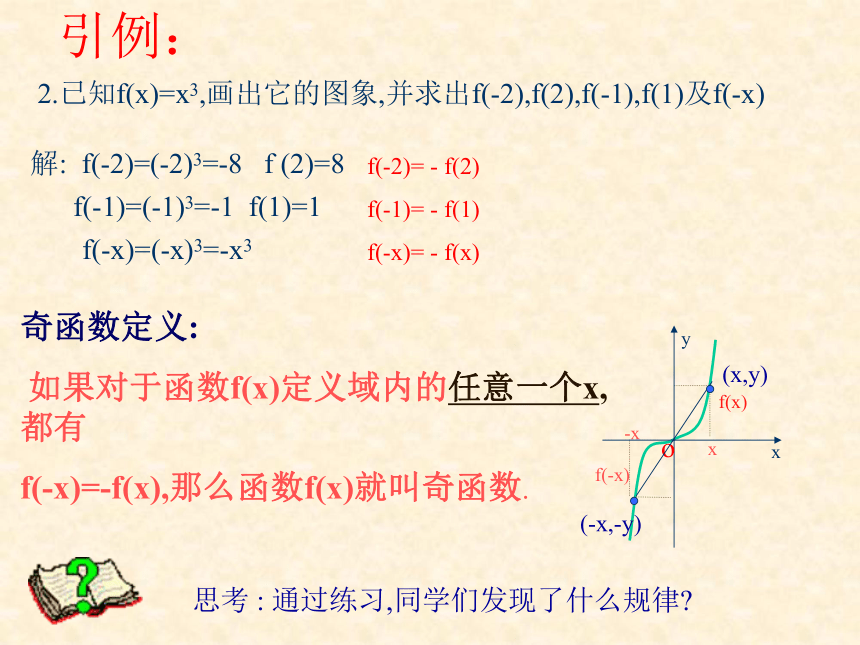
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8 f (2)=8f(-1)=(-1)3=-1 f(1)=1 f(-x)=(-x)3=-x3思考 : 通过练习,同学们发现了什么规律?f(-2)= - f(2)
f(-1)= - f(1)
f(-x)= - f(x)-xf(-x)xf(x)奇函数定义:
如果对于函数f(x)定义域内的任意一个x, 都有
f(-x)=-f(x),那么函数f(x)就叫奇函数.1.函数奇偶性的概念: 偶函数定义:
如果对于函数f(x)定义域内任意一个x, 都有
f(-x)=f(x), 那么函数f(x)就叫偶函数. 奇函数定义:
如果对于函数f(x)定义域内的任意一个x, 都有
f(-x)=-f(x),那么函数f(x)就叫奇函数.☆对奇函数、偶函数定义的说明:(1). 定义域关于原点对称是函数具有奇偶性的必要条件。 (2).奇、偶函数定义的逆命题也成立,即:
若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)
具有奇偶性。例1. 判断下列函数的奇偶性(1) f(x)=x3+2x (2) f(x)=2x4+3x2解:∵对定义域内每一个x都有 f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)即 f(-x)= - f(x)∴f(x)为奇函数 ∵对定义域内每一个x都有 f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数定义域为R解:定义域为R即 f(-x)= f(x)-1≦x ≦1且x ≠0∴定义域为[-1,0) ∪(0,1]即f(-x)= - f(x)∴ f(x) 为奇函数. ⑴先求定义域,看是否关于原点对称;
⑵再判断f(-x)= -f(x)或f(-x)=f(x) 是否成立。☆ 说明:用定义判断函数奇偶性的步骤:练习1. 判断下列函数的奇偶性(2) f(x)= - x2 +1∴f(x)为奇函数 ∵对定义域内每一个x都有 f(-x)= -(-x)2+1
= - x2+1
∴f(x)为偶函数解:定义域为﹛x|x≠0﹜解:定义域为R即 f(-x)= - f(x)即 f(-x)= f(x)∵对定义域内每一个x都有 (3). f(x)=5 (4) f(x)=0解: (3) f(x)的定义域为R
∵对定义域内每一个x都有
f(-x)=f(x)=5
∴f(x)为偶函数解: (4)定义域为R
∵对定义域内每一个x都有
f(-x)=f(x)=0 又 f(-x)=-f(x)=0
∴f(x)为既奇又偶函数说明: 函数f(x)=0 (定义域关于原点对称),为既奇又偶函数。 (5). f(x)=x+1 (6). f(x)=x2 x∈[- 1 , 3]解: (5) ∵ f(-x)= -x+1
- f(x)= -x-1
∴f(-x)≠f(x)
且f(-x)≠ –f(x)
∴f(x)为非奇非偶函数解: (6)∵定义域不关于原点
对 称
∴f(x)为非奇非偶函数解: (8) 定义域为 [0 ,+∞)
∵ 定义域不关于原点对称
∴f(x)为非奇非偶函数 奇函数
说明:根据奇偶性, 偶函数
函数可划分为四类: 既奇又偶函数
非奇非偶函数练习2. 说出下列函数的奇偶性:偶函数奇函数奇函数奇函数(1)f(x)=x4 ________ (2) f(x)= x -1 __________(3) f(x)=x ________奇函数(4)f(x)=x -2 __________偶函数(5) f(x)=x5 __________(6)f(x)=x -3 _______________ 说明:(1) 对于形如 f(x)=x n 的函数, 若n为偶数,则它为偶函数。若n为奇数,则它为奇函数。(7) f(x)=x-1+x__________(8)f(x)=x4 + x 2 ________奇函数偶函数(2)偶函数与偶函数的和函数是偶函数
奇函数与奇函数的和函数是奇函数奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))2.奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数.⑵ 偶函数的图象关于y轴对称. 反之, 如果一个函数的图象关于 y 轴对称,那 么这个函数是偶函数.注:奇偶函数图象的性质可用于:
①.简化函数图象的画法。
②.判断函数的奇偶性。本课小结:1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x) f(x)为奇函数。
如果都有f(-x)= f(x) f(x)为偶函数。2.两个性质:
一个函数为奇函数 它的图象关于原点对称。一个函数为偶函数 它的图象关于y 轴对称。 作业:
课本 36页1,2 思考题:2.设y=f(x)为定义在R上的奇函数,当x > 0时,f(x)=x(x-1) , 画出函数f(x)图象,并求出函数的解析式1.已知y=f(x)是偶函数,且在(-∞,0)上是增函数,则
y=f(x)在(0,∞)上是增函数还是减函数,并证明你的判断.同学们再见!
1.3.2函数的奇偶性引例:1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1),及f(-x) ,并画出它的图象。解:f(-2)=(-2)2=4 f(2)=4f(-1)=(-1)2=1 f(1)=1f(-x)=(-x)2=x2-xxf(-x)f(x)f(-2)=f(2)
f(-1)=f(1)
f(-x)=f(x)思考 : 通过练习,同学们发现了什么规律?偶函数定义:
如果对于函数f(x)定义域内任意一个x, 都有
f(-x)=f(x), 那么函数f(x)就叫偶函数.引例:
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8 f (2)=8f(-1)=(-1)3=-1 f(1)=1 f(-x)=(-x)3=-x3思考 : 通过练习,同学们发现了什么规律?f(-2)= - f(2)
f(-1)= - f(1)
f(-x)= - f(x)-xf(-x)xf(x)奇函数定义:
如果对于函数f(x)定义域内的任意一个x, 都有
f(-x)=-f(x),那么函数f(x)就叫奇函数.1.函数奇偶性的概念: 偶函数定义:
如果对于函数f(x)定义域内任意一个x, 都有
f(-x)=f(x), 那么函数f(x)就叫偶函数. 奇函数定义:
如果对于函数f(x)定义域内的任意一个x, 都有
f(-x)=-f(x),那么函数f(x)就叫奇函数.☆对奇函数、偶函数定义的说明:(1). 定义域关于原点对称是函数具有奇偶性的必要条件。 (2).奇、偶函数定义的逆命题也成立,即:
若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)
具有奇偶性。例1. 判断下列函数的奇偶性(1) f(x)=x3+2x (2) f(x)=2x4+3x2解:∵对定义域内每一个x都有 f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)即 f(-x)= - f(x)∴f(x)为奇函数 ∵对定义域内每一个x都有 f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数定义域为R解:定义域为R即 f(-x)= f(x)-1≦x ≦1且x ≠0∴定义域为[-1,0) ∪(0,1]即f(-x)= - f(x)∴ f(x) 为奇函数. ⑴先求定义域,看是否关于原点对称;
⑵再判断f(-x)= -f(x)或f(-x)=f(x) 是否成立。☆ 说明:用定义判断函数奇偶性的步骤:练习1. 判断下列函数的奇偶性(2) f(x)= - x2 +1∴f(x)为奇函数 ∵对定义域内每一个x都有 f(-x)= -(-x)2+1
= - x2+1
∴f(x)为偶函数解:定义域为﹛x|x≠0﹜解:定义域为R即 f(-x)= - f(x)即 f(-x)= f(x)∵对定义域内每一个x都有 (3). f(x)=5 (4) f(x)=0解: (3) f(x)的定义域为R
∵对定义域内每一个x都有
f(-x)=f(x)=5
∴f(x)为偶函数解: (4)定义域为R
∵对定义域内每一个x都有
f(-x)=f(x)=0 又 f(-x)=-f(x)=0
∴f(x)为既奇又偶函数说明: 函数f(x)=0 (定义域关于原点对称),为既奇又偶函数。 (5). f(x)=x+1 (6). f(x)=x2 x∈[- 1 , 3]解: (5) ∵ f(-x)= -x+1
- f(x)= -x-1
∴f(-x)≠f(x)
且f(-x)≠ –f(x)
∴f(x)为非奇非偶函数解: (6)∵定义域不关于原点
对 称
∴f(x)为非奇非偶函数解: (8) 定义域为 [0 ,+∞)
∵ 定义域不关于原点对称
∴f(x)为非奇非偶函数 奇函数
说明:根据奇偶性, 偶函数
函数可划分为四类: 既奇又偶函数
非奇非偶函数练习2. 说出下列函数的奇偶性:偶函数奇函数奇函数奇函数(1)f(x)=x4 ________ (2) f(x)= x -1 __________(3) f(x)=x ________奇函数(4)f(x)=x -2 __________偶函数(5) f(x)=x5 __________(6)f(x)=x -3 _______________ 说明:(1) 对于形如 f(x)=x n 的函数, 若n为偶数,则它为偶函数。若n为奇数,则它为奇函数。(7) f(x)=x-1+x__________(8)f(x)=x4 + x 2 ________奇函数偶函数(2)偶函数与偶函数的和函数是偶函数
奇函数与奇函数的和函数是奇函数奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))2.奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数.⑵ 偶函数的图象关于y轴对称. 反之, 如果一个函数的图象关于 y 轴对称,那 么这个函数是偶函数.注:奇偶函数图象的性质可用于:
①.简化函数图象的画法。
②.判断函数的奇偶性。本课小结:1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x) f(x)为奇函数。
如果都有f(-x)= f(x) f(x)为偶函数。2.两个性质:
一个函数为奇函数 它的图象关于原点对称。一个函数为偶函数 它的图象关于y 轴对称。 作业:
课本 36页1,2 思考题:2.设y=f(x)为定义在R上的奇函数,当x > 0时,f(x)=x(x-1) , 画出函数f(x)图象,并求出函数的解析式1.已知y=f(x)是偶函数,且在(-∞,0)上是增函数,则
y=f(x)在(0,∞)上是增函数还是减函数,并证明你的判断.同学们再见!
