实数(含有教学过程)
图片预览




文档简介
慧通文府(百日学通)教育科技有限公司教研部
实数
一、本章学习目标
1.了解算数平方根、平方根、立方根的概念,会用根号表示数的平方根、立方根。
2.了解开方与乘方互为逆运算,会用平方运算求某些非负数是平方根,会用 立方根运算求某些数的立方根。
3.了解无理数和实数的概念,知道实数与数轴上的点是一一对应,有序实数对与平面上的点是一一对应的;了解数的范围由有理数扩大到实数后,概念运算等的一致性。
4.能用有理数估计一个无理数的大致范围。
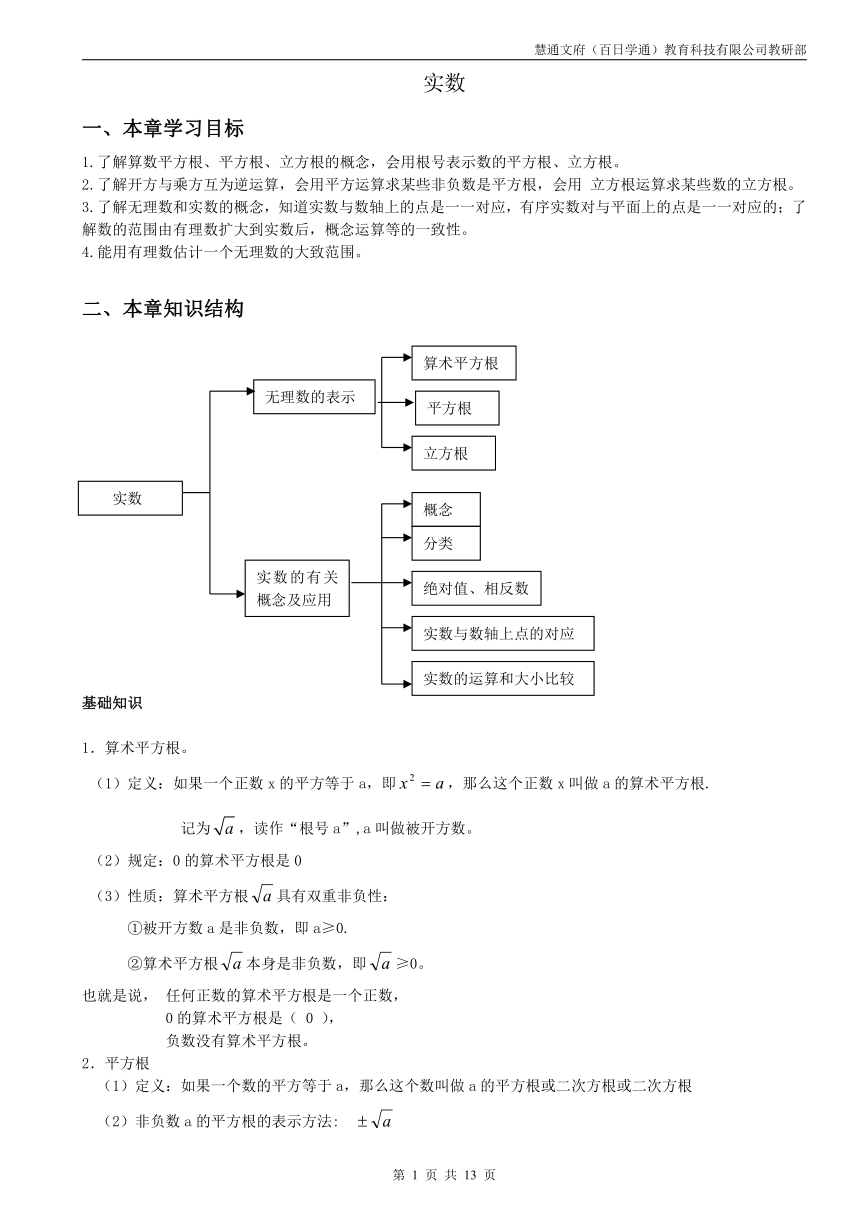
二、本章知识结构
基础知识
1.算术平方根。
(1)定义:如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根.
记为,读作“根号a”,a叫做被开方数。
(2)规定:0的算术平方根是0
(3)性质:算术平方根具有双重非负性:
①被开方数a是非负数,即a≥0.
②算术平方根本身是非负数,即≥0。
也就是说, 任何正数的算术平方根是一个正数,
0的算术平方根是( 0 ),
负数没有算术平方根。
2.平方根
(1)定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根或二次方根
(2)非负数a的平方根的表示方法:
(3)性质: 一个正数有两个平方根,这两个平方根互为相反数。
0 只有一个平方根,它是0 。
负数没有平方根。
说明:平方根有三种表示形式:± , ,-,它们的意义分别是
:非负数a的平方根,非负数a的算术平方根,非负数a的负平方根。要特别注意: ≠±。
3.平方根与算术平方根的区别与联系:
区别:①定义不同算术平方根要求是正数
②个数不同平方根有2个,算术平方根1个
③ 表示方法不同:算术平方根为,平方根为±
联系:①具有包含关系:
②存在条件相同:
③ 0的平方根和算术平方根都是0。
4.a2的算术平方根的性质
a (a≥0)
=│a│=
-a (a<0)
从算术平方根的定义可得:=a (a≥0)
5.立方根
(1) 定义:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根
(2) 数a的立方根的表示方法:
(3) 互为相反数的两个数的立方根之间的关系:互为相反数
(4) 两个重要的公式
6.开方运算:
(1)定义:
①开平方运算:求一个数a的平方根的运算叫做开平方。
②开立方运算:求一个数立方根的运算叫做开立方
(2)平方与开平方是互逆关系,故在运算结果中可以相互检验。
7.无理数的定义
无限不循环小数叫做无理数
8.有理数与无理数的区别
有理数总可以用有限小数或无限循环小数表示;反过来,任何有限小数或无限循环小数也都是有理数。而无理数是无限不循环小数小数,有理数和无理数区别之根本是有限及无限循环和无限不循环。有理数可以化成分数,无理数不能化成分数。
9.常见的无理数类型
(1)一般的无限不循环小数,如:1.41421356¨···
(2)看似循环而实际不循环的小数,如0.1010010001···(相邻两个1之间0的个数逐次加1)。
(3)有特定意义的数,如:π=3.14159265···
(4)开方开不尽的数。如:。
10.实数
(1)概念:有理数和 无理数统称为实数。
(2)分类 按定义
正整数
整数 0
负整数
有理数 有限小数或无限循环小数
正分数
实数 分数
负分数
正无理数
无理数 无限不循环小数
负无理数
按大小 正实数
实数 零
负实数
(3)实数的有关性质
①a与b互为相反数〈=〉a+b=0
②a与b互为倒数〈=〉ab=1
③任何实数的绝对值都是非负数,即≥0
④互为相反数的两个数的绝对值相等, 即=
⑤正数的倒数是正数;负数的倒数是负数;零没有倒数.
⑥一个正实数的绝对值是它本身,负实数的绝对值是它的相反数,0的绝对值是0
(4)实数和数轴上的点的对应关系:
实数和数轴上的点是一一对应的关系
实数的大小比较
在数轴上表示的两个数,右边的数总比左边的数大。
正数大于零;零大于负数;正数大于一切负数;两个负数比较,绝对值大的反而小。
(5)实数中的非负数及其性质
在实数范围内,正数和零统称为非负数
我们已经学过的非负数有如下三种形式
①任何一个实数a的绝对值是非负数,即≥0
②任何一个实数的平方是非负数,即≥0;
③任何一个非负数a的算术平方根是非负数,即≥0
非负数有以下性质
①非负数有最小值零
②有限个非负数之和仍然是非负数
③几个非负数之和等于0,则每个非负数都等于0。
三、本章重点难点
1.本章的主要内容是平方根、立方根的概念和求法,实数的有关概念和运算。本章重点是算数平方根和平方根的概念和求法,它们是理解立方根的概念和求法、实数的意义和运算的直接基础.
2.本章的难点是平方根和实数的概念。
四、本章中考考试内容和考试要求
1.了解算数平方根、平方根、立方根、实数的概念;会用根号表示算数平方根、平方根、立方根;会求无理数的相反数、绝对值。
2.知道实数与数轴上的点是一一对应关系,会有理数估计无理数的大致范围,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会进行简单的实数运算,会借助数轴比较有理数的大小。
3.会利用绝对值的知识 解决化简问题和非负数问题。
五、教学计划
课时 讲课内容 约授课时间/分钟 约练习时间/分钟
一个课时 平方根 平方根的相关概念
算术平方根
开平方
立方根 立方根的相关概念
开立方
实数 实数的定义
实数的运算
实数的有关性质
实数综合测试
六、教学过程
对学生的要求:熟记1——20的平方数:
熟记1——20的平方数:
(一)平方根
1、平方根的相关概念
平方根:如果一个数x的平方等于a,那么这个数就叫做a的平方根或二次方根
用公式表示
平方根的性质:①一个正数有两个平方根,一正一负,并且它们互为相反数
②零的平方根是零
③负数没有平方根
例1:求下列各数的平方根:(1);(2)0.81;(3)900;(4)361
解:(1)因为,所以的平方根是
(2)因为,所以0.81的平方根是
(3)因为,所以900的平方根是
(4)因为,所以361的平方根是
实数练习题1:
如下列数有平方根的,求出该数的平方根:
1、;2、;3、;4、1000;5、0;6、;7、121;8、;9、;10、
2、算术平方根
算术平方根:数a的正的那个平方根就叫做a的算术平方根;0的算术平方根是0
算术平方根的性质:①被开方数a是非负数
②算术平方根本身是非负数
例2:求下列各式的值:(1);(2);(3)
解:(1)由于表示10000的算术平方根,且,所以
(2)由于表示144的负的平方根,且,所以
(3)由于表示625的平方根,且,所以
实数练习题2:
1、;2、;3、;4、;5、;6、;7、;8、;
9、;10、
3、开平方
开平方:求一个数a的平方根的运算,叫做开平方
开平方与平方互为逆运算
例3:求使下列各式有意义的x的取值范围:(1);(2);(3);(4)
解:(1)由,解得,当时,有意义
(2)由,解得,当时,有意义
(3)因为不论x取任何值时,,所以x取任何值时,总有意义
(4)由,解得;由于分母不能为0,所以
所以当时,有意义
实数练习题3:
求使下列各式有意义的x的取值范围:
1、;2、;3、;4、;5、;6、;7、;
8、;9、
例4:求下列各式中x的值:(1);(2)
解:(1)因为,所以,所以
又因为,所以
(2)因为,所以
又因为,所以
当时,;当时,,所以或
实数练习题4:
求下列各式中x的值:
1、;2、;3、;4、;5、 x 2-3.24=0;6、4x2=49;7、x2-1.69=0;
8、(x+9)2=169;9、
4、立方根的相关概念
如果一个数的立方等于a,那么这个数叫做a的立方根;用式子表示为
立方根的性质:①正数有一个正的立方根
②负数有一个负的立方根
③0有一个立方根,就是0本身
例5:求下列各数的立方根:(1)343;(2);(3);(4)4
解:(1)因为,所以
(2)因为,,所以
(3)因为,所以
(4)4的立方根为
实数练习题5:
1、64;2、-125;3、;4、1000;5、-1;6、;7、;8、;9、;10、0.512
5、开立方
例6:求下列各式的值:(1);(2);(3)
解:(1) (2) (3)
实数练习题6:
求下列各式的值:
1、;2、;3、;4、;5、;6、;7、;8、
9、;10、
例7:求下列各式中的x的值:(1);(2);(3)
解:(1)由题意得,所以
(2)由题意得,即
(3)由题意得,即,所以
实数练习题7:
求下列各式中的x的值:
1、;2、(x-1)3=-0.125;3、;4、;5、
6、实数
实数:有理数和无理数的统称
无理数:无限不循环小数
例8:把下列各数分别填入相应的集合中:,3.14159265,,0.6,0,-8,,,
有理数集合:
无理数集合:
实数练习题8:
1、圈出下列数中得有理数: ,0.123333333……,0, 0.123, 29;
2、下列数中,无理数是: 3.141414, 33% , 9.0000000 , ,,
3、在, ,3,, ,中,实数是:
例9:计算(1)
解:
=
实数习题9:计算:
1、; 2、; 3、
4、;5、;6、
实数的有关性质
⑴a与b互为相反数〈=〉a+b=0
⑵a与b互为倒数〈=〉ab=1
⑶任何实数的绝对值都是非负数,即≥0
⑷互为相反数的两个数的绝对值相等, 即=
⑸正数的倒数是正数;负数的倒数是负数;零没有倒数.
例10:若、互为相反数,、互为负倒数,则
解:由题意可知 a+b=0 , cd=1
练习10
1. 的相反数是( )
A. B. C. D.
2. 下列各组数中,互为相反数的是( )
A.2和 B.-2和- C. -2和|-2| D.和
3. 的倒数是( )
A. B. C. D.
4. 实数a在数轴上对应的点如图所示,则a、-a、1的大小关系正确的是
A.-a<a<1 B.a<-a<1
C.1<-a<a D.a<1<-a
5. 若,b是a的倒数,c是a的相反数,求a+b-c的值
实数和数轴上的点的对应关系:
实数和数轴上的点是一一对应的关系
(5) 实数的大小比较
1. 在数轴上表示的两个数,右边的数总比左边的数大。
2. 正数大于零,零大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小。
例11:计算:
解:
=
练习11
1. 比大的实数是( )
A. B. C. D.
2. 比较大小: 4.9; .(填“>”或“<”)
3. 比较大小: ; ; 2.35.(填“>”或“<”)
4. 满足的整数是 .
5. 若规定误差小于1, 那么的估算值为( )
A. 3 B. 7 C. 8 D. 7或8
6. 估计( )
A.7~8之间 B. 8.0~8.5之间 C. 8.5~9.0之间 D.9.0~9.5之间
7. 如图,在数轴上表示实数的点可能是( )
A.点 B.点 C.点 D.点
8. 已知b9. 已知数a在数轴上的对应点的位置如图所示,
则化简
10. a,b的大小关系如右图所示,化简
11.已知a是的整数部分,b是它的小数部分,求的值
12.已知,b是a的小数部分,求ab的值。
(6) 实数中的非负数及其性质
在实数范围内,正数和零统称为非负数
我们已经学过的非负数有如下三种形式
⑴任何一个实数a的绝对值是非负数,即≥0
⑵任何一个实数的平方是非负数,即≥0;
⑶任何一个非负数a的算术平方根是非负数,即≥0
非负数有以下性质
⑴非负数有最小值零
⑵有限个非负数之和仍然是非负数
⑶几个非负数之和等于0,则每个非负数都等于0。
例12:,求的值
解:由于
所以a+2=0 , b-1=0 , c+3=0
a=-2 , b=1 , c= -3
练习12
1. 若 HYPERLINK "http://www." EMBED Equation.DSMT4 ,则 .
2. 已知,则
3. 已知,则
4. 已知实数a , b 在数轴上的对应点的位置如图所示,化简=
5. 的值.
实数综合测试(一)
姓名:___________ 分数:___________
一、填空题(每小题4分,共28分)
1.和是_____________的平方根.
2. 的算术平方根是_____________.
3. 化简:
4. 若,则;若,则.
5.的相反数是__________;的绝对值是_____________.
6. 若,则
7.满足的整数是_____________.
二、选择题(每小题4分,共16分)
8. 使式子有意义的的取值范围为( )
A. B. C. D.
9. 实数范围内,一个数与它的倒数相等的有( )
A.个 B.个 C.个 D.个
10. 若,则 ( )A. B. C. D.
11.在实数-、0.32、、0.2、、、中,无理数的个数是( )
A.3 B.4 C.5 D.6
三、解答题(共56分)
12. 求下列式子中的x:(每小题5分,共20分)
①x2-625=0 ②(x+9)2=144
③(x-1)3=-0.729 ④
13. 计算:(每小题5分,共10分)
(1) (2)-+
14.已知是n-m+3的算数平方根,是吗、m+2n的立方根,求B-A的值
15. 若,求的平方根.(13分)
实数水平测试(二)
姓名:___________ 分数:___________
一、选择题(每题4分,共24分)
6. 在下列实数中,无理数是( )
7. 下列计算错误的是( )
A.-(-2)=2 B. C.2+3=5 D.
8. 如图,在数轴上表示实数的点可能是( )
A.点 B.点 C.点 D.点
9. 估计78的立方根的大小在( )
A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间
10. 的相反数是( )
A. B. C. D.
11. 下列说法正确的是( )
A.的平方根是 B.将点向右平移5个单位长度到点
C.是无理数 D.点关于轴的对称点是
二、填空题(每题3分,共18分)
12. 化简=_________。
13. 计算的结果是 .
14. 的倒数是
15. 比较大小:3 。
16. 的平方根是
17. 若实数满足,则的值是 .
三、计算(每题4分,共8分)
18. 计算:
19. 计算
20. 求下列式子中的x:(每小题5分,共20分)
①x2-225=0 ②(x-3)2=144
③(x-1)3= 512 ④
四、解答题(每题10分,共30分)
21. 已知,则求
22. 若与互为相反数,求
23. 已知,求
无理数的表示
算术平方根
平方根
立方根
实数的有关概念及应用
概念
分类
绝对值、相反数
实数与数轴上点的对应
实数的运算和大小比较
实数
1
0
2
3
4
N
M
Q
P
1
0
2
3
4
N
M
Q
P
第4题图
a
1
0
第 3 页 共 13 页
实数
一、本章学习目标
1.了解算数平方根、平方根、立方根的概念,会用根号表示数的平方根、立方根。
2.了解开方与乘方互为逆运算,会用平方运算求某些非负数是平方根,会用 立方根运算求某些数的立方根。
3.了解无理数和实数的概念,知道实数与数轴上的点是一一对应,有序实数对与平面上的点是一一对应的;了解数的范围由有理数扩大到实数后,概念运算等的一致性。
4.能用有理数估计一个无理数的大致范围。
二、本章知识结构
基础知识
1.算术平方根。
(1)定义:如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根.
记为,读作“根号a”,a叫做被开方数。
(2)规定:0的算术平方根是0
(3)性质:算术平方根具有双重非负性:
①被开方数a是非负数,即a≥0.
②算术平方根本身是非负数,即≥0。
也就是说, 任何正数的算术平方根是一个正数,
0的算术平方根是( 0 ),
负数没有算术平方根。
2.平方根
(1)定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根或二次方根
(2)非负数a的平方根的表示方法:
(3)性质: 一个正数有两个平方根,这两个平方根互为相反数。
0 只有一个平方根,它是0 。
负数没有平方根。
说明:平方根有三种表示形式:± , ,-,它们的意义分别是
:非负数a的平方根,非负数a的算术平方根,非负数a的负平方根。要特别注意: ≠±。
3.平方根与算术平方根的区别与联系:
区别:①定义不同算术平方根要求是正数
②个数不同平方根有2个,算术平方根1个
③ 表示方法不同:算术平方根为,平方根为±
联系:①具有包含关系:
②存在条件相同:
③ 0的平方根和算术平方根都是0。
4.a2的算术平方根的性质
a (a≥0)
=│a│=
-a (a<0)
从算术平方根的定义可得:=a (a≥0)
5.立方根
(1) 定义:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根
(2) 数a的立方根的表示方法:
(3) 互为相反数的两个数的立方根之间的关系:互为相反数
(4) 两个重要的公式
6.开方运算:
(1)定义:
①开平方运算:求一个数a的平方根的运算叫做开平方。
②开立方运算:求一个数立方根的运算叫做开立方
(2)平方与开平方是互逆关系,故在运算结果中可以相互检验。
7.无理数的定义
无限不循环小数叫做无理数
8.有理数与无理数的区别
有理数总可以用有限小数或无限循环小数表示;反过来,任何有限小数或无限循环小数也都是有理数。而无理数是无限不循环小数小数,有理数和无理数区别之根本是有限及无限循环和无限不循环。有理数可以化成分数,无理数不能化成分数。
9.常见的无理数类型
(1)一般的无限不循环小数,如:1.41421356¨···
(2)看似循环而实际不循环的小数,如0.1010010001···(相邻两个1之间0的个数逐次加1)。
(3)有特定意义的数,如:π=3.14159265···
(4)开方开不尽的数。如:。
10.实数
(1)概念:有理数和 无理数统称为实数。
(2)分类 按定义
正整数
整数 0
负整数
有理数 有限小数或无限循环小数
正分数
实数 分数
负分数
正无理数
无理数 无限不循环小数
负无理数
按大小 正实数
实数 零
负实数
(3)实数的有关性质
①a与b互为相反数〈=〉a+b=0
②a与b互为倒数〈=〉ab=1
③任何实数的绝对值都是非负数,即≥0
④互为相反数的两个数的绝对值相等, 即=
⑤正数的倒数是正数;负数的倒数是负数;零没有倒数.
⑥一个正实数的绝对值是它本身,负实数的绝对值是它的相反数,0的绝对值是0
(4)实数和数轴上的点的对应关系:
实数和数轴上的点是一一对应的关系
实数的大小比较
在数轴上表示的两个数,右边的数总比左边的数大。
正数大于零;零大于负数;正数大于一切负数;两个负数比较,绝对值大的反而小。
(5)实数中的非负数及其性质
在实数范围内,正数和零统称为非负数
我们已经学过的非负数有如下三种形式
①任何一个实数a的绝对值是非负数,即≥0
②任何一个实数的平方是非负数,即≥0;
③任何一个非负数a的算术平方根是非负数,即≥0
非负数有以下性质
①非负数有最小值零
②有限个非负数之和仍然是非负数
③几个非负数之和等于0,则每个非负数都等于0。
三、本章重点难点
1.本章的主要内容是平方根、立方根的概念和求法,实数的有关概念和运算。本章重点是算数平方根和平方根的概念和求法,它们是理解立方根的概念和求法、实数的意义和运算的直接基础.
2.本章的难点是平方根和实数的概念。
四、本章中考考试内容和考试要求
1.了解算数平方根、平方根、立方根、实数的概念;会用根号表示算数平方根、平方根、立方根;会求无理数的相反数、绝对值。
2.知道实数与数轴上的点是一一对应关系,会有理数估计无理数的大致范围,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会进行简单的实数运算,会借助数轴比较有理数的大小。
3.会利用绝对值的知识 解决化简问题和非负数问题。
五、教学计划
课时 讲课内容 约授课时间/分钟 约练习时间/分钟
一个课时 平方根 平方根的相关概念
算术平方根
开平方
立方根 立方根的相关概念
开立方
实数 实数的定义
实数的运算
实数的有关性质
实数综合测试
六、教学过程
对学生的要求:熟记1——20的平方数:
熟记1——20的平方数:
(一)平方根
1、平方根的相关概念
平方根:如果一个数x的平方等于a,那么这个数就叫做a的平方根或二次方根
用公式表示
平方根的性质:①一个正数有两个平方根,一正一负,并且它们互为相反数
②零的平方根是零
③负数没有平方根
例1:求下列各数的平方根:(1);(2)0.81;(3)900;(4)361
解:(1)因为,所以的平方根是
(2)因为,所以0.81的平方根是
(3)因为,所以900的平方根是
(4)因为,所以361的平方根是
实数练习题1:
如下列数有平方根的,求出该数的平方根:
1、;2、;3、;4、1000;5、0;6、;7、121;8、;9、;10、
2、算术平方根
算术平方根:数a的正的那个平方根就叫做a的算术平方根;0的算术平方根是0
算术平方根的性质:①被开方数a是非负数
②算术平方根本身是非负数
例2:求下列各式的值:(1);(2);(3)
解:(1)由于表示10000的算术平方根,且,所以
(2)由于表示144的负的平方根,且,所以
(3)由于表示625的平方根,且,所以
实数练习题2:
1、;2、;3、;4、;5、;6、;7、;8、;
9、;10、
3、开平方
开平方:求一个数a的平方根的运算,叫做开平方
开平方与平方互为逆运算
例3:求使下列各式有意义的x的取值范围:(1);(2);(3);(4)
解:(1)由,解得,当时,有意义
(2)由,解得,当时,有意义
(3)因为不论x取任何值时,,所以x取任何值时,总有意义
(4)由,解得;由于分母不能为0,所以
所以当时,有意义
实数练习题3:
求使下列各式有意义的x的取值范围:
1、;2、;3、;4、;5、;6、;7、;
8、;9、
例4:求下列各式中x的值:(1);(2)
解:(1)因为,所以,所以
又因为,所以
(2)因为,所以
又因为,所以
当时,;当时,,所以或
实数练习题4:
求下列各式中x的值:
1、;2、;3、;4、;5、 x 2-3.24=0;6、4x2=49;7、x2-1.69=0;
8、(x+9)2=169;9、
4、立方根的相关概念
如果一个数的立方等于a,那么这个数叫做a的立方根;用式子表示为
立方根的性质:①正数有一个正的立方根
②负数有一个负的立方根
③0有一个立方根,就是0本身
例5:求下列各数的立方根:(1)343;(2);(3);(4)4
解:(1)因为,所以
(2)因为,,所以
(3)因为,所以
(4)4的立方根为
实数练习题5:
1、64;2、-125;3、;4、1000;5、-1;6、;7、;8、;9、;10、0.512
5、开立方
例6:求下列各式的值:(1);(2);(3)
解:(1) (2) (3)
实数练习题6:
求下列各式的值:
1、;2、;3、;4、;5、;6、;7、;8、
9、;10、
例7:求下列各式中的x的值:(1);(2);(3)
解:(1)由题意得,所以
(2)由题意得,即
(3)由题意得,即,所以
实数练习题7:
求下列各式中的x的值:
1、;2、(x-1)3=-0.125;3、;4、;5、
6、实数
实数:有理数和无理数的统称
无理数:无限不循环小数
例8:把下列各数分别填入相应的集合中:,3.14159265,,0.6,0,-8,,,
有理数集合:
无理数集合:
实数练习题8:
1、圈出下列数中得有理数: ,0.123333333……,0, 0.123, 29;
2、下列数中,无理数是: 3.141414, 33% , 9.0000000 , ,,
3、在, ,3,, ,中,实数是:
例9:计算(1)
解:
=
实数习题9:计算:
1、; 2、; 3、
4、;5、;6、
实数的有关性质
⑴a与b互为相反数〈=〉a+b=0
⑵a与b互为倒数〈=〉ab=1
⑶任何实数的绝对值都是非负数,即≥0
⑷互为相反数的两个数的绝对值相等, 即=
⑸正数的倒数是正数;负数的倒数是负数;零没有倒数.
例10:若、互为相反数,、互为负倒数,则
解:由题意可知 a+b=0 , cd=1
练习10
1. 的相反数是( )
A. B. C. D.
2. 下列各组数中,互为相反数的是( )
A.2和 B.-2和- C. -2和|-2| D.和
3. 的倒数是( )
A. B. C. D.
4. 实数a在数轴上对应的点如图所示,则a、-a、1的大小关系正确的是
A.-a<a<1 B.a<-a<1
C.1<-a<a D.a<1<-a
5. 若,b是a的倒数,c是a的相反数,求a+b-c的值
实数和数轴上的点的对应关系:
实数和数轴上的点是一一对应的关系
(5) 实数的大小比较
1. 在数轴上表示的两个数,右边的数总比左边的数大。
2. 正数大于零,零大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小。
例11:计算:
解:
=
练习11
1. 比大的实数是( )
A. B. C. D.
2. 比较大小: 4.9; .(填“>”或“<”)
3. 比较大小: ; ; 2.35.(填“>”或“<”)
4. 满足的整数是 .
5. 若规定误差小于1, 那么的估算值为( )
A. 3 B. 7 C. 8 D. 7或8
6. 估计( )
A.7~8之间 B. 8.0~8.5之间 C. 8.5~9.0之间 D.9.0~9.5之间
7. 如图,在数轴上表示实数的点可能是( )
A.点 B.点 C.点 D.点
8. 已知b
则化简
10. a,b的大小关系如右图所示,化简
11.已知a是的整数部分,b是它的小数部分,求的值
12.已知,b是a的小数部分,求ab的值。
(6) 实数中的非负数及其性质
在实数范围内,正数和零统称为非负数
我们已经学过的非负数有如下三种形式
⑴任何一个实数a的绝对值是非负数,即≥0
⑵任何一个实数的平方是非负数,即≥0;
⑶任何一个非负数a的算术平方根是非负数,即≥0
非负数有以下性质
⑴非负数有最小值零
⑵有限个非负数之和仍然是非负数
⑶几个非负数之和等于0,则每个非负数都等于0。
例12:,求的值
解:由于
所以a+2=0 , b-1=0 , c+3=0
a=-2 , b=1 , c= -3
练习12
1. 若 HYPERLINK "http://www." EMBED Equation.DSMT4 ,则 .
2. 已知,则
3. 已知,则
4. 已知实数a , b 在数轴上的对应点的位置如图所示,化简=
5. 的值.
实数综合测试(一)
姓名:___________ 分数:___________
一、填空题(每小题4分,共28分)
1.和是_____________的平方根.
2. 的算术平方根是_____________.
3. 化简:
4. 若,则;若,则.
5.的相反数是__________;的绝对值是_____________.
6. 若,则
7.满足的整数是_____________.
二、选择题(每小题4分,共16分)
8. 使式子有意义的的取值范围为( )
A. B. C. D.
9. 实数范围内,一个数与它的倒数相等的有( )
A.个 B.个 C.个 D.个
10. 若,则 ( )A. B. C. D.
11.在实数-、0.32、、0.2、、、中,无理数的个数是( )
A.3 B.4 C.5 D.6
三、解答题(共56分)
12. 求下列式子中的x:(每小题5分,共20分)
①x2-625=0 ②(x+9)2=144
③(x-1)3=-0.729 ④
13. 计算:(每小题5分,共10分)
(1) (2)-+
14.已知是n-m+3的算数平方根,是吗、m+2n的立方根,求B-A的值
15. 若,求的平方根.(13分)
实数水平测试(二)
姓名:___________ 分数:___________
一、选择题(每题4分,共24分)
6. 在下列实数中,无理数是( )
7. 下列计算错误的是( )
A.-(-2)=2 B. C.2+3=5 D.
8. 如图,在数轴上表示实数的点可能是( )
A.点 B.点 C.点 D.点
9. 估计78的立方根的大小在( )
A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间
10. 的相反数是( )
A. B. C. D.
11. 下列说法正确的是( )
A.的平方根是 B.将点向右平移5个单位长度到点
C.是无理数 D.点关于轴的对称点是
二、填空题(每题3分,共18分)
12. 化简=_________。
13. 计算的结果是 .
14. 的倒数是
15. 比较大小:3 。
16. 的平方根是
17. 若实数满足,则的值是 .
三、计算(每题4分,共8分)
18. 计算:
19. 计算
20. 求下列式子中的x:(每小题5分,共20分)
①x2-225=0 ②(x-3)2=144
③(x-1)3= 512 ④
四、解答题(每题10分,共30分)
21. 已知,则求
22. 若与互为相反数,求
23. 已知,求
无理数的表示
算术平方根
平方根
立方根
实数的有关概念及应用
概念
分类
绝对值、相反数
实数与数轴上点的对应
实数的运算和大小比较
实数
1
0
2
3
4
N
M
Q
P
1
0
2
3
4
N
M
Q
P
第4题图
a
1
0
第 3 页 共 13 页
