函数模型
图片预览



文档简介
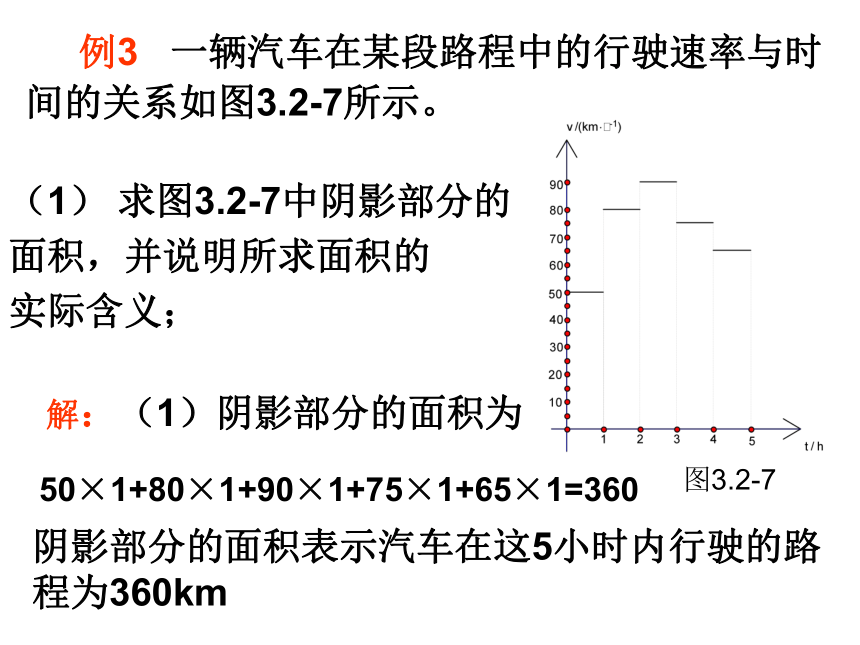
课件16张PPT。函数模型的应用实例一、新课引入到目前为止,我们已经学习了哪些常用函数?一次函数二次函数指数函数对数函数幂函数 例3 一辆汽车在某段路程中的行驶速率与时
间的关系如图3.2-7所示。(1) 求图3.2-7中阴影部分的
面积,并说明所求面积的
实际含义;解:(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360阴影部分的面积表示汽车在这5小时内行驶的路
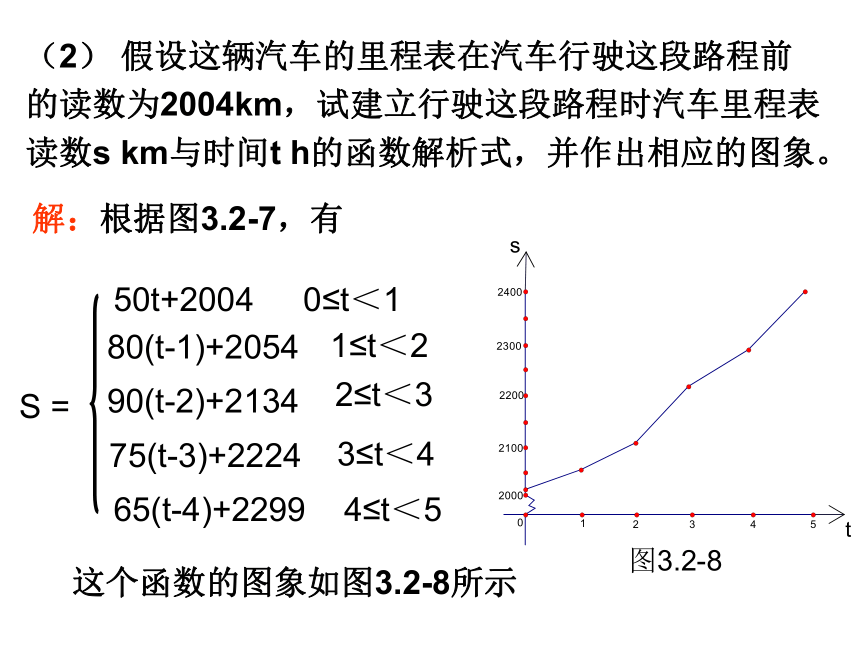
程为360km图3.2-7(2) 假设这辆汽车的里程表在汽车行驶这段路程前
的读数为2004km,试建立行驶这段路程时汽车里程表
读数s km与时间t h的函数解析式,并作出相应的图象。解:根据图3.2-7,有S =50t+2004 80(t-1)+205490(t-2)+213475(t-3)+222465(t-4)+22990≤t<11≤t<22≤t<33≤t<44≤t<5这个函数的图象如图3.2-8所示图3.2-8ts解函数的应用问题,一般地可按以下四步进行:第一步:阅读理解,认真审题第二步:引进数学符号,建立数学模型第三步:利用数学的方法将得到的常规数学问题
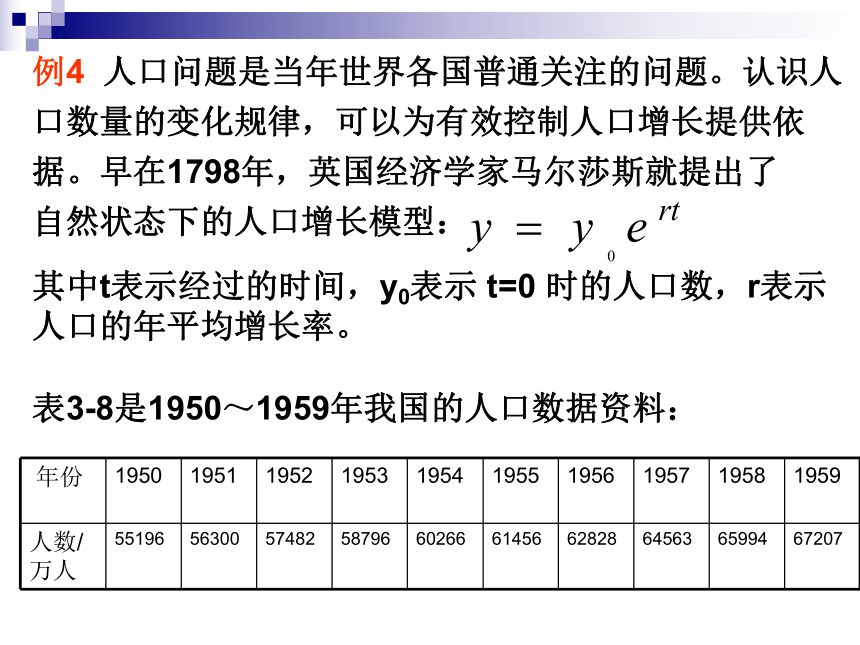
(即数学模型)予以解答,求得结果第四步:再转移成具体问题作出解答例4 人口问题是当年世界各国普通关注的问题。认识人
口数量的变化规律,可以为有效控制人口增长提供依
据。早在1798年,英国经济学家马尔莎斯就提出了
自然状态下的人口增长模型:表3-8是1950~1959年我国的人口数据资料:其中t表示经过的时间,y0表示 t=0 时的人口数,r表示
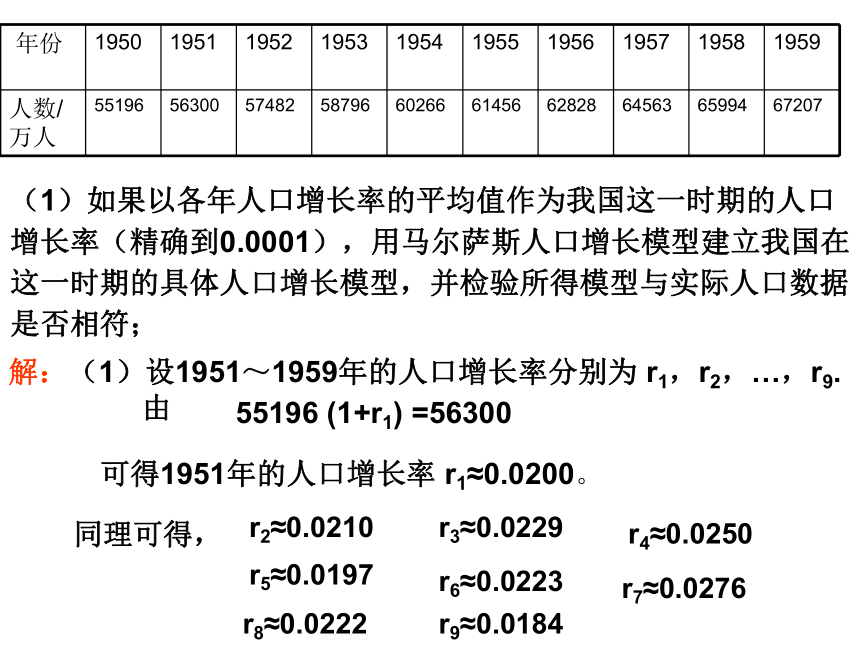
人口的年平均增长率。(1)如果以各年人口增长率的平均值作为我国这一时期的人口
增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在
这一时期的具体人口增长模型,并检验所得模型与实际人口数据
是否相符;解:(1)设1951~1959年的人口增长率分别为 r1,r2,…,r9.
由55196 (1+r1) =56300可得1951年的人口增长率 r1≈0.0200。同理可得,r2≈0.0210r3≈0.0229r4≈0.0250r5≈0.0197r6≈0.0223r7≈0.0276r8≈0.0222r9≈0.0184于是,1951~1959年期间,我国人口的年均增长率为r=(r1+r2+···+r9)÷9≈0.0221令y0=55196,则我国在1950~1959年期间的人口增长模型为根据表3-8中的数据作出散点图,
并作出函数的图象(图3.2-9)。由图3.2-9可以看出,所得模型与
1951~1959年的实际人口数据
基本吻合。t(2)如果按表3-8的增长趋势,大约在哪一年我国的
人口达到13亿?解:将 y=130000代入所以,如果按表3-8的增长趋势,那么大约在1950年
后的第39年(即1989年)我国的人口就已达到13亿。
由此可以看到,如果不实行计划生育,而是让人口
自然增长,今天我国将面临难以承受的人口压力。
例5 某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示: 请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?分析:由表中信息可知①销售单价每增加1元,日均销售量就减少40桶②销售利润怎样计算较好?
`解:设在进价基础上增加x元后,日均经营利润为y
元,则有日均销售量为 (桶) 而 有最大值 只需将销售单价定为11.5元,就可获得最大的利润。 思考1:上表提供的数据对应的散点图大致如何? 思考2:根据这些点的分布情况,可以选用那个函数模型进行拟合,使它能比较近似地反映这个地区未成年男性体重y(kg)与身高 x(cm)的函数关系? 思考5:若体重超过相同身高男性体重的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175cm, 体重为78kg的在校男生的体重是否正常? 思考3:怎样确定拟合函数中参数a,b的值? 思考4:如何检验函数 的拟合程度? 思考6:你能总结一下用拟合函数解决应用性问题的基本过程吗? 收集数据用函数模型解释实际问题No
间的关系如图3.2-7所示。(1) 求图3.2-7中阴影部分的
面积,并说明所求面积的
实际含义;解:(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360阴影部分的面积表示汽车在这5小时内行驶的路
程为360km图3.2-7(2) 假设这辆汽车的里程表在汽车行驶这段路程前
的读数为2004km,试建立行驶这段路程时汽车里程表
读数s km与时间t h的函数解析式,并作出相应的图象。解:根据图3.2-7,有S =50t+2004 80(t-1)+205490(t-2)+213475(t-3)+222465(t-4)+22990≤t<11≤t<22≤t<33≤t<44≤t<5这个函数的图象如图3.2-8所示图3.2-8ts解函数的应用问题,一般地可按以下四步进行:第一步:阅读理解,认真审题第二步:引进数学符号,建立数学模型第三步:利用数学的方法将得到的常规数学问题
(即数学模型)予以解答,求得结果第四步:再转移成具体问题作出解答例4 人口问题是当年世界各国普通关注的问题。认识人
口数量的变化规律,可以为有效控制人口增长提供依
据。早在1798年,英国经济学家马尔莎斯就提出了
自然状态下的人口增长模型:表3-8是1950~1959年我国的人口数据资料:其中t表示经过的时间,y0表示 t=0 时的人口数,r表示
人口的年平均增长率。(1)如果以各年人口增长率的平均值作为我国这一时期的人口
增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在
这一时期的具体人口增长模型,并检验所得模型与实际人口数据
是否相符;解:(1)设1951~1959年的人口增长率分别为 r1,r2,…,r9.
由55196 (1+r1) =56300可得1951年的人口增长率 r1≈0.0200。同理可得,r2≈0.0210r3≈0.0229r4≈0.0250r5≈0.0197r6≈0.0223r7≈0.0276r8≈0.0222r9≈0.0184于是,1951~1959年期间,我国人口的年均增长率为r=(r1+r2+···+r9)÷9≈0.0221令y0=55196,则我国在1950~1959年期间的人口增长模型为根据表3-8中的数据作出散点图,
并作出函数的图象(图3.2-9)。由图3.2-9可以看出,所得模型与
1951~1959年的实际人口数据
基本吻合。t(2)如果按表3-8的增长趋势,大约在哪一年我国的
人口达到13亿?解:将 y=130000代入所以,如果按表3-8的增长趋势,那么大约在1950年
后的第39年(即1989年)我国的人口就已达到13亿。
由此可以看到,如果不实行计划生育,而是让人口
自然增长,今天我国将面临难以承受的人口压力。
例5 某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示: 请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?分析:由表中信息可知①销售单价每增加1元,日均销售量就减少40桶②销售利润怎样计算较好?
`解:设在进价基础上增加x元后,日均经营利润为y
元,则有日均销售量为 (桶) 而 有最大值 只需将销售单价定为11.5元,就可获得最大的利润。 思考1:上表提供的数据对应的散点图大致如何? 思考2:根据这些点的分布情况,可以选用那个函数模型进行拟合,使它能比较近似地反映这个地区未成年男性体重y(kg)与身高 x(cm)的函数关系? 思考5:若体重超过相同身高男性体重的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175cm, 体重为78kg的在校男生的体重是否正常? 思考3:怎样确定拟合函数中参数a,b的值? 思考4:如何检验函数 的拟合程度? 思考6:你能总结一下用拟合函数解决应用性问题的基本过程吗? 收集数据用函数模型解释实际问题No
