2.3幂函数及其性质
图片预览





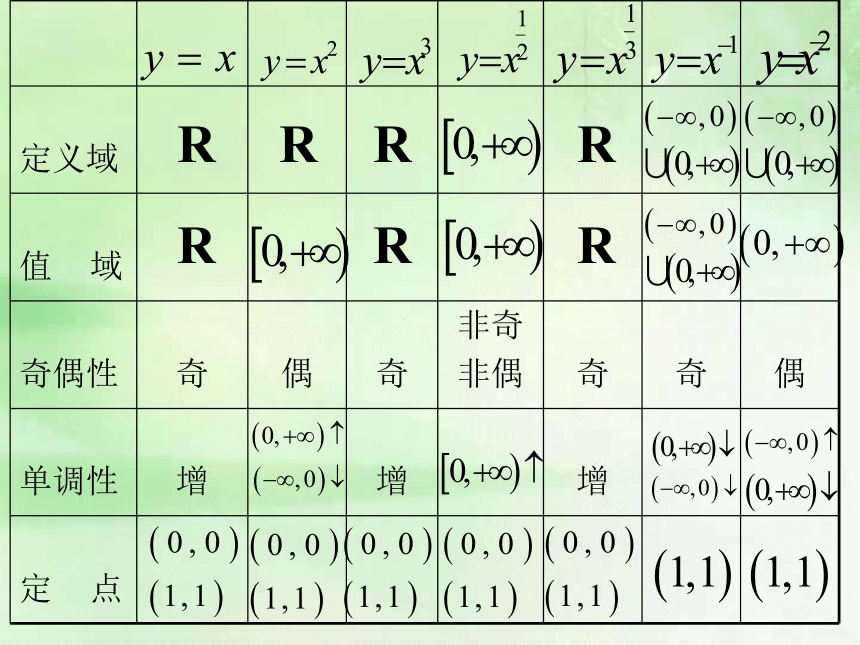

文档简介
课件15张PPT。幂函数及其性质学习目标一、知识目标:
1.通过实例了解并记住幂函数的概念.
2.结合几个常见幂函数的图象观察图象特征并能自行发现幂函数的性质.
3.记住幂函数的性质并会应用.
4.了解幂函数模型的实际应用.
能力目标:
通过观察图象特征来归纳函数性质,
从而培养学生数形结合的能力.
情感目标:
通过观察图象体会数学的简洁美.
一、幂函数的概念的引入 阅读课本第85页的具体实例(1)-(5),思考下列问题:
1.它们的解析式分别是什么?若用 表示自变量, 表示 的函数,上述五个函数解析式分别是什么?
答案:
都是以幂的底为自变量的函数,即形如:
2.以上问题中的函数有什么共同特征?
一般地函数 叫幂函数.思考:1.幂函数与指数函数有什么区别?
2.判断下列函数是否为幂函数?二、幂函数的图象特征及性质注意(1)先求定义域再列表描点;
(2)观察你画出的函数图象,寻找这些函数的图象特征.再观察图象,归纳幂函数的图象特征和性质:1.?>0时,
(1)图象都经过点(0,0)和(1,1);
(2)图象在第一象限是上升的,即在 上是增函数.
(3)图象呈“抛物线”型的弧.
2. ?<0时,(1)图象都经过点(1,1);
(2)图象在第一象限是下降的,且向右无限接近X轴,向上无限接近Y轴,即
在 上是减函数.
(3)图象呈“双曲线”型的弧.
由刚才实验可以得出:
3.在直线x=1右侧,幂指数越大,图象越高,即越远离x轴;即x>1时,当函数的自变量相等时,幂指数越大,函数值越大
思考:在直线x=1左侧呢?再观察图象,可以得到什么结论?例4 幂函数f(x)=xa ,f(x)=xb ,f(x)=xc, f(x)=xd,在第一象限的图象如图所示,则a,b,c,d的大小关系 是( ) (A)a>b>c>d (B)d>b>c>a (C)d>c>b>a (D)b>c>d>a 答案:D小结:1.记住幂函数的定义;
2.掌握幂函数的图象和性质;
3.能利用幂函数的性质解决有关问题;
4.这节课我们从观察图象入手,运用自然语言描述了函数的图象特征,最后抽象到运用数学语言和符号刻画了相应的数量特征. 这是一个循序渐进的过程,这也是数学学习和研究中经常使用的方法.
作业:1.课本87页第3题.
2.思考:指数函数、对数函数与幂函数之间有什么联系?再见!
1.通过实例了解并记住幂函数的概念.
2.结合几个常见幂函数的图象观察图象特征并能自行发现幂函数的性质.
3.记住幂函数的性质并会应用.
4.了解幂函数模型的实际应用.
能力目标:
通过观察图象特征来归纳函数性质,
从而培养学生数形结合的能力.
情感目标:
通过观察图象体会数学的简洁美.
一、幂函数的概念的引入 阅读课本第85页的具体实例(1)-(5),思考下列问题:
1.它们的解析式分别是什么?若用 表示自变量, 表示 的函数,上述五个函数解析式分别是什么?
答案:
都是以幂的底为自变量的函数,即形如:
2.以上问题中的函数有什么共同特征?
一般地函数 叫幂函数.思考:1.幂函数与指数函数有什么区别?
2.判断下列函数是否为幂函数?二、幂函数的图象特征及性质注意(1)先求定义域再列表描点;
(2)观察你画出的函数图象,寻找这些函数的图象特征.再观察图象,归纳幂函数的图象特征和性质:1.?>0时,
(1)图象都经过点(0,0)和(1,1);
(2)图象在第一象限是上升的,即在 上是增函数.
(3)图象呈“抛物线”型的弧.
2. ?<0时,(1)图象都经过点(1,1);
(2)图象在第一象限是下降的,且向右无限接近X轴,向上无限接近Y轴,即
在 上是减函数.
(3)图象呈“双曲线”型的弧.
由刚才实验可以得出:
3.在直线x=1右侧,幂指数越大,图象越高,即越远离x轴;即x>1时,当函数的自变量相等时,幂指数越大,函数值越大
思考:在直线x=1左侧呢?再观察图象,可以得到什么结论?例4 幂函数f(x)=xa ,f(x)=xb ,f(x)=xc, f(x)=xd,在第一象限的图象如图所示,则a,b,c,d的大小关系 是( ) (A)a>b>c>d (B)d>b>c>a (C)d>c>b>a (D)b>c>d>a 答案:D小结:1.记住幂函数的定义;
2.掌握幂函数的图象和性质;
3.能利用幂函数的性质解决有关问题;
4.这节课我们从观察图象入手,运用自然语言描述了函数的图象特征,最后抽象到运用数学语言和符号刻画了相应的数量特征. 这是一个循序渐进的过程,这也是数学学习和研究中经常使用的方法.
作业:1.课本87页第3题.
2.思考:指数函数、对数函数与幂函数之间有什么联系?再见!
