初一数学单元测试

相交线与平行线单元测试题
一、填空题(每小题3分，共30分)
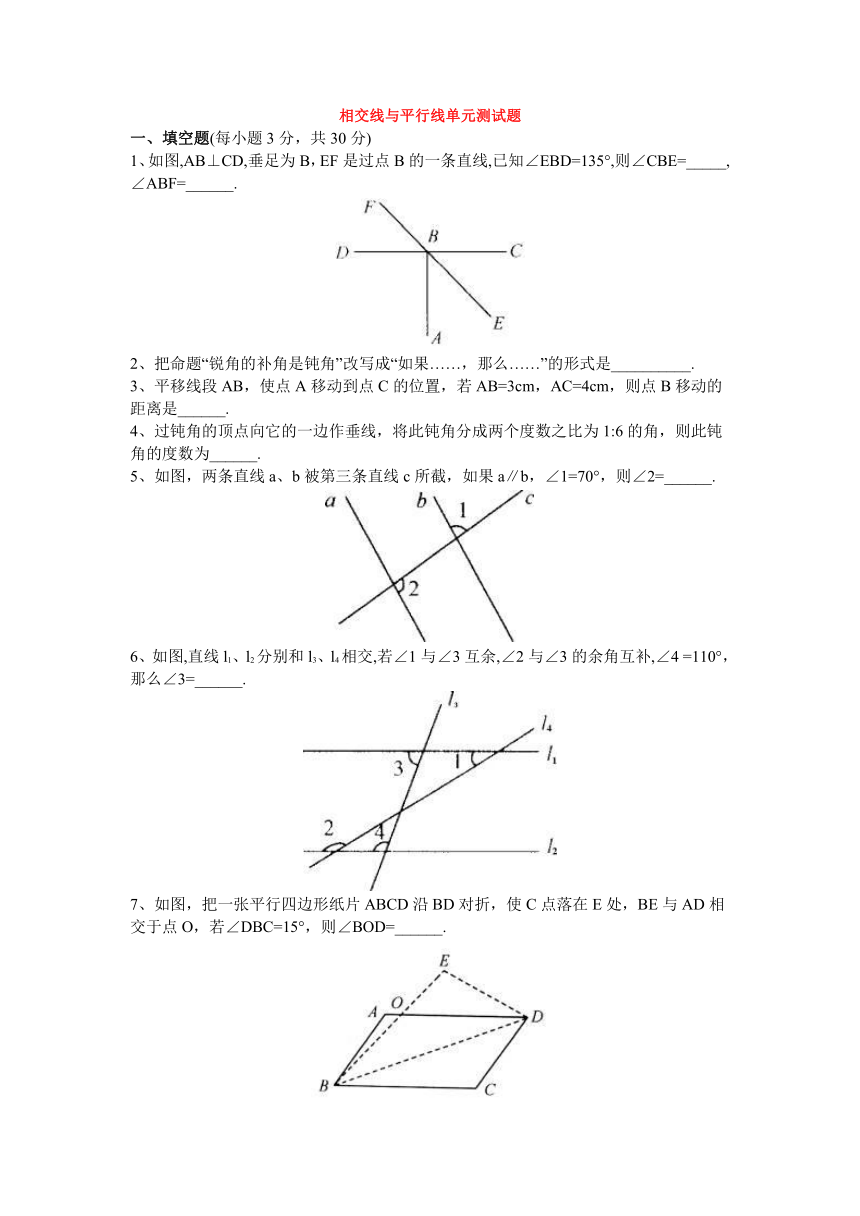
1、如图,AB⊥CD,垂足为B，EF是过点B的一条直线,已知∠EBD=135°,则∠CBE=_____, ∠ABF=______.
2、把命题“锐角的补角是钝角”改写成“如果……，那么……”的形式是__________.
3、平移线段AB，使点A移动到点C的位置，若AB=3cm，AC=4cm，则点B移动的距离是______.
4、过钝角的顶点向它的一边作垂线，将此钝角分成两个度数之比为1:6的角，则此钝角的度数为______.
5、如图，两条直线a、b被第三条直线c所截，如果a∥b，∠1=70°，则∠2=______.
6、如图,直线l1、l2分别和l3、l4相交,若∠1与∠3互余,∠2与∠3的余角互补,∠4 =110°，那么∠3=______.
7、如图，把一张平行四边形纸片ABCD沿BD对折，使C点落在E处，BE与AD相交于点O，若∠DBC=15°，则∠BOD=______.
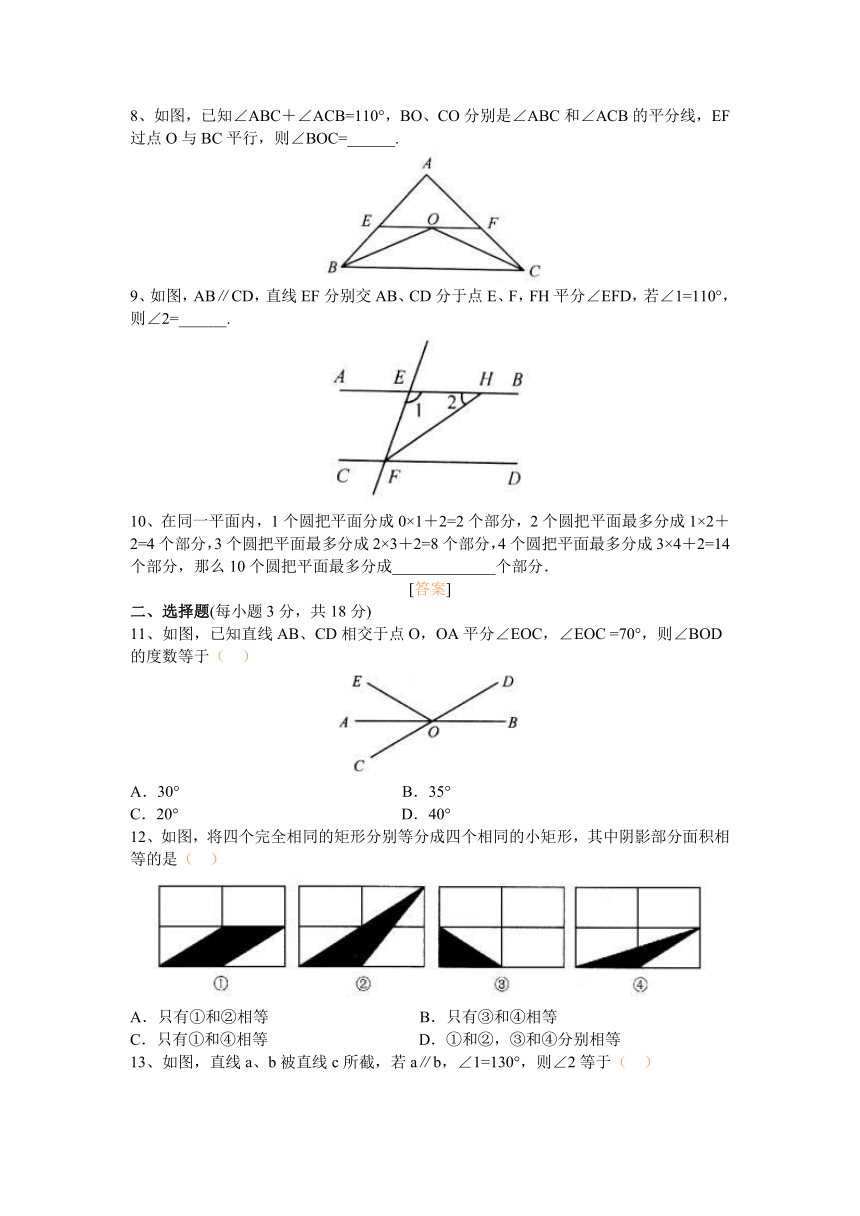
8、如图，已知∠ABC＋∠ACB=110°，BO、CO分别是∠ABC和∠ACB的平分线，EF过点O与BC平行，则∠BOC=______.
9、如图，AB∥CD，直线EF分别交AB、CD分于点E、F，FH平分∠EFD，若∠1=110°，则∠2=______.
10、在同一平面内，1个圆把平面分成0×1＋2=2个部分，2个圆把平面最多分成1×2＋2=4个部分，3个圆把平面最多分成2×3＋2=8个部分，4个圆把平面最多分成3×4＋2=14个部分，那么10个圆把平面最多分成_____________个部分．
[答案 ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )]
二、选择题(每小题3分，共18分)
11、如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC =70°，则∠BOD的度数等于（　） ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )
A．30°　　　　　　　　　　　　　　B．35°
C．20°　　　　　　　　　　　　　　D．40°
12、如图，将四个完全相同的矩形分别等分成四个相同的小矩形，其中阴影部分面积相等的是（　） ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )
A．只有①和②相等　　　　　　　　　 B．只有③和④相等
C．只有①和④相等　　　　　　　　　 D．①和②，③和④分别相等
13、如图，直线a、b被直线c所截，若a∥b，∠1=130°，则∠2等于（　） ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )
A．30°　　　　　　　　　　　　　　 B．40°
C．50°　　　　　　　　　　　　　　 D．60°
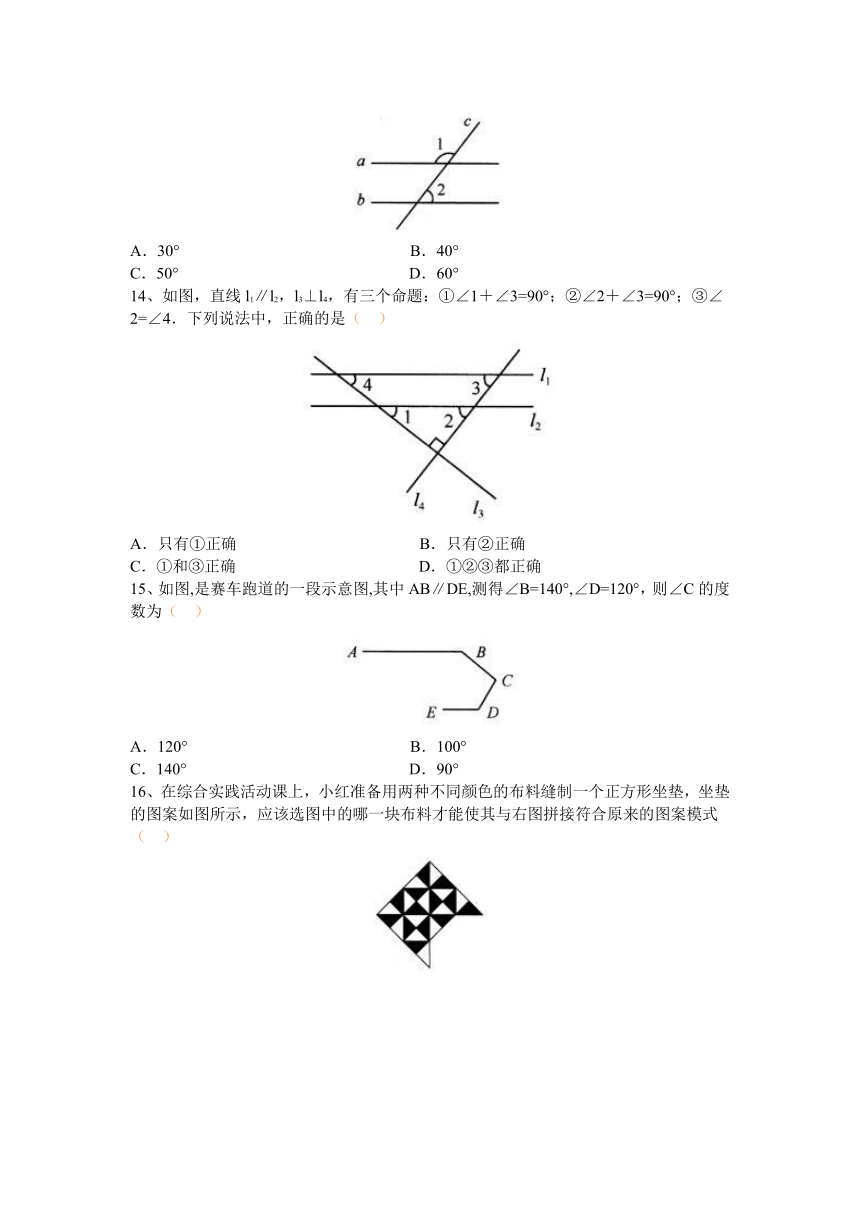
14、如图，直线l1∥l2，l3⊥l4，有三个命题：①∠1＋∠3=90°；②∠2＋∠3=90°；③∠2=∠4．下列说法中，正确的是（　） ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )
A．只有①正确　　　　　　　　　　　 B．只有②正确
C．①和③正确　　　　　　　　　　　 D．①②③都正确
15、如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°，则∠C的度数为（　） ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )
A．120°　　　　　　　　　　　　　　B．100°
C．140°　　　　　　　　　　　　　　D．90°
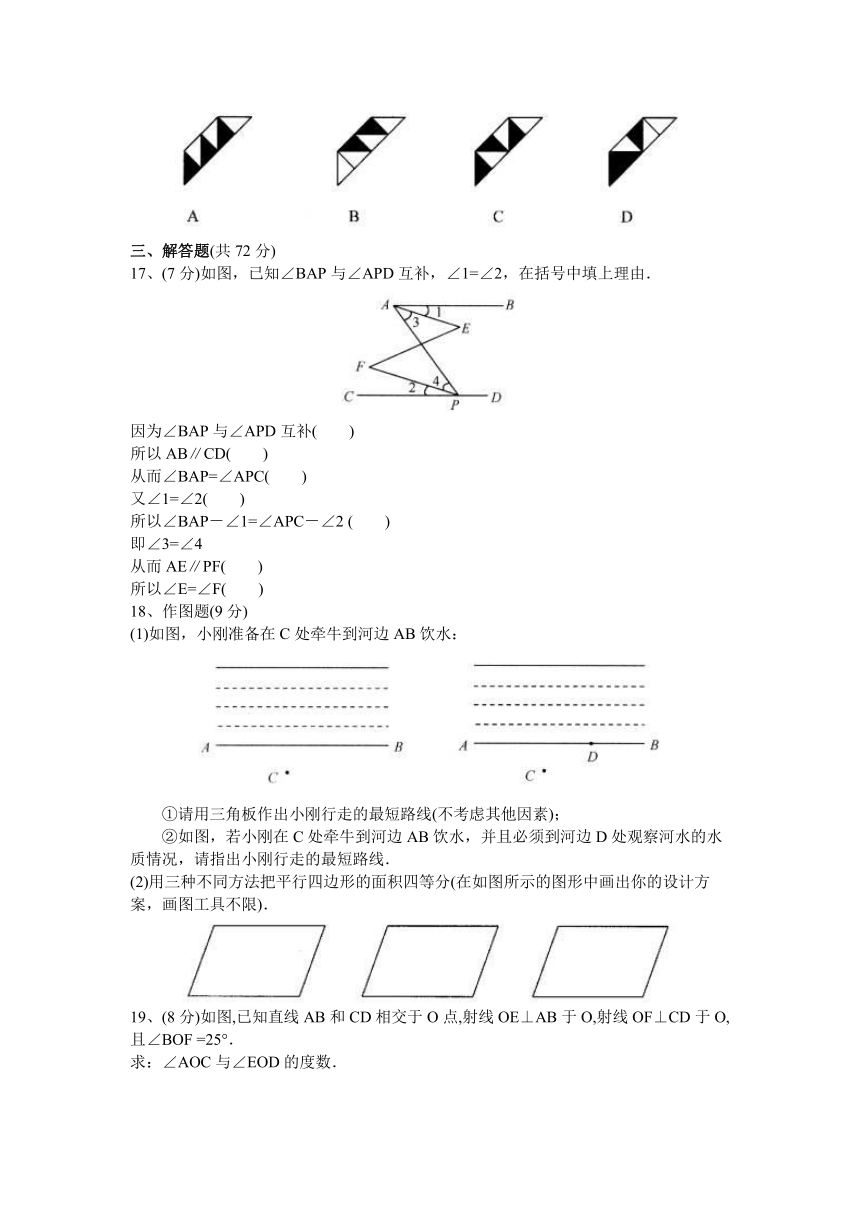
16、在综合实践活动课上，小红准备用两种不同颜色的布料缝制一个正方形坐垫，坐垫的图案如图所示，应该选图中的哪一块布料才能使其与右图拼接符合原来的图案模式（　） ( file: / / / E:\\初一\\压缩文件\\压缩文件\\相交线与平行线单元测试题\\SX_11_01_019\\index.html" \l "# )
三、解答题(共72分)
17、(7分)如图，已知∠BAP与∠APD互补，∠1=∠2，在括号中填上理由．
因为∠BAP与∠APD互补(　　)
所以AB∥CD(　　)
从而∠BAP=∠APC(　　)
又∠1=∠2(　　)
所以∠BAP－∠1=∠APC－∠2 (　　)
即∠3=∠4
从而AE∥PF(　　)
所以∠E=∠F(　　)
18、作图题(9分)
(1)如图，小刚准备在C处牵牛到河边AB饮水：
　　①请用三角板作出小刚行走的最短路线(不考虑其他因素)；
　　②如图，若小刚在C处牵牛到河边AB饮水，并且必须到河边D处观察河水的水质情况，请指出小刚行走的最短路线．
(2)用三种不同方法把平行四边形的面积四等分(在如图所示的图形中画出你的设计方案，画图工具不限)．
19、(8分)如图,已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF =25°．
求：∠AOC与∠EOD的度数．
20、(6分)如图，依据图形，找出能使AD∥BC成立的条件(至少6个)．
21、(8分)已知：如图，DE⊥AC，∠AGF=∠ABC，∠1＋∠2=180°，试判断BF与AC的位置关系，并说明理由．
22、(8分)如图所示，已知直线a∥b，直线c和直线a、b交于C、D两点，在C、D之间有一点M，如果点M在C、D之间运动，问∠1、∠2、∠3之间有怎样的关系？这种关系是否发生变化？
23、(12分)已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C(如图)．
(1)你能得出CE∥BF这一结论吗？
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗？若能，写出你得出结论的过程．
24、(14分)如图a)，已知直线m∥n，A、B为直线n上的两点，C、P为直线m上的两点，其中A、B、C为三个定点，点P在m上移动，我们知道，无论P点移动到任何位置总有△ABP与△ABC的面积相等，其理由是：______________________________________。
　　解决问题：
　　如图b)，五边形ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图所示的形状，但承包土地与开垦荒地的分界小路(图中折线CDE)还保留着，张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案．(不计分界小路与直路的占地面积)．
　　(1)写出设计方案，并在图中画出相应的图形；
　　(2)说明方案设计理由．
答案
答案：
　　1、45°；135°
　　2、如果一个角是锐角，那么它的补角是钝角
　　3、4cm　　　　　4、105°
　　5、110°　　　　6、70°
　　7、150°　　　　8、125°
9、35°　　　　10、92
选择
B D C A B C
17、已知；
　　同旁内角互补，两直线平行；
　　两直线平行，内错角相等；
　　已知；
　　等式的性质；
　　内错角相等，两直线平行；
　　两直线平行，内错角相等．
18、
　　(1)①过点C作CM⊥AB垂足为M，则CM为最短路线(图略)；
　　②联结CD，则线段CD为最短路线(图略)
　　(2)提供以下四种方案：
19、∵OF⊥CD，∴∠COF=90°．
　　∵∠BOF=25°，∴∠BOC=90°－∠BOF=65°
　　∴∠AOC=180°－∠BOC=115°．
　　∵OE⊥AB，∴∠AOE=90°．
　　∵∠AOD=∠BOC，
　　∴∠EOD=90°－∠AOD=25°
　　(∠EOD与∠BOF都是∠EOF的余角)
20、
　　内错角相等：∠ADB=∠CBD，∠ADC=∠DCH等
　　同旁内角互补：∠BAD＋∠ABC=180°，
　　∠ADC＋∠BCD=180°等
　　AD∥EF，且BC∥EF；…
　　同位角相等：∠GAD=∠ABC；…
21、BF⊥AC，理由如下：
　　∵∠AGF=∠ABC，∴GF∥BC，∴∠1=∠3．
　　∵∠1＋∠2=180°，∴∠2＋∠3=180°．
　　 ∴BF∥DE． ∴∠BFC=∠DEC．
　　∵DE⊥AC，∴∠DEC=90°．
　　 ∴∠BFC=90°． ∴BF⊥AC．
22、∠1＋∠3=∠2；这种关系不变化．
(过点M作直线与a或b平行)．
23、(1)能得到；
　　(2)能得到．
　　∵∠2=∠1，∠1=∠4，∴∠2=∠4． ∴EC∥BF．
　　∴∠C=∠3．又∵∠B=∠C，∴∠B=∠3．
　　∴AB∥CD． ∴∠A=∠D．
24、
　　因为平行线间的距离相等，所以无论点P在m上移动到任何位置，总有△ABP与△ABC同底等高，因此，它们的面积总相等．
　　解决问题：(1)画法如图．
　　联结EC，过点D作DF∥EC，交CM于点F，联结EF，EF即为所求直路的位置；
　　(2)设EF交CD于点H，由上面得到的结论，可知：
　　　 S△ECF=S△ECD，S△HCF=S△EDH．
　　∴S五边形ABCDE= S五边形ABCFE，S五边形EDCMN= S四边形EFMN．