角平分线的性质定理及其逆定理

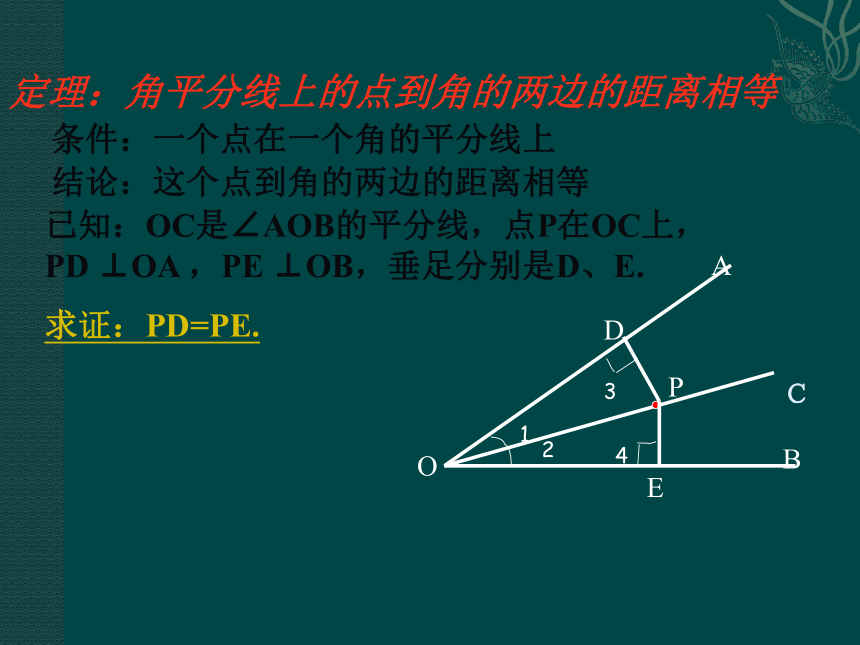
课件22张PPT。如图:若想在两条公路围成的A区域内建一个化工厂，为了减少环境污染,要求化工厂到桥头的距离是500米，同时为了交通方便,要求化工厂到两条公路的距离相等，假如你是工程师，你能在图上找到化工厂的位置吗?桥头焦寺旁堤刘（比例尺为１：５００００）A区域定理：角平分线上的点到角的两边的距离相等条件：一个点在一个角的平分线上结论：这个点到角的两边的距离相等已知：OC是∠AOB的平分线，点P在OC上，PD ⊥OA ，PE ⊥OB，垂足分别是D、E.
求证：PD=PE.Ｃ1234一.角平分线的性质定理：角平分线上的点到角的两边的距离相等用符号语言表示为：∵∠1= ∠2
PD ⊥OA ，PE ⊥OB
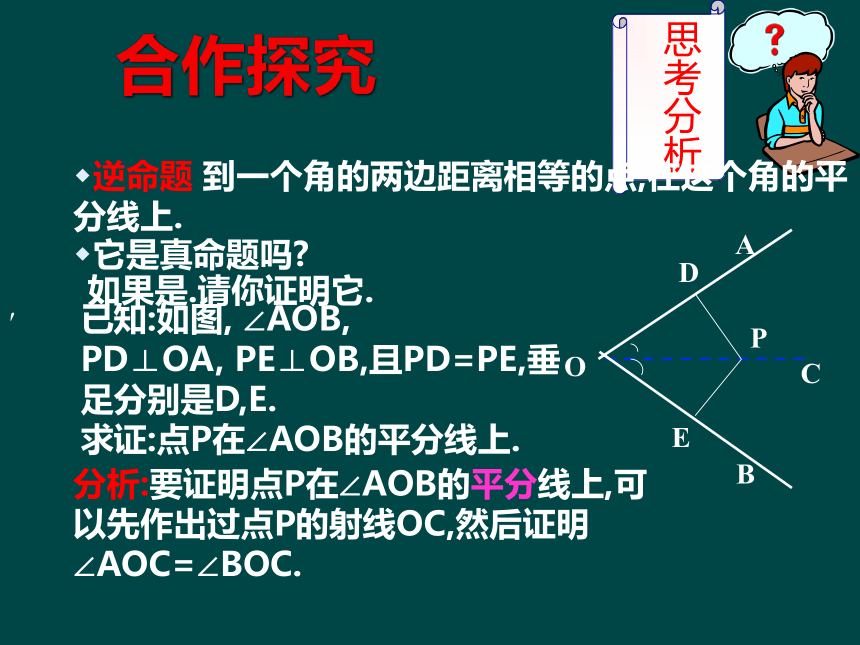
∴PD=PE.交换定理的条件和结论得到的命题为：合作探究′逆命题 到一个角的两边距离相等的点,在这个角的平分线上.它是真命题吗?如果是.请你证明它.已知:如图, ∠AOB,
PD⊥OA, PE⊥OB,且PD=PE,垂足分别是D,E.
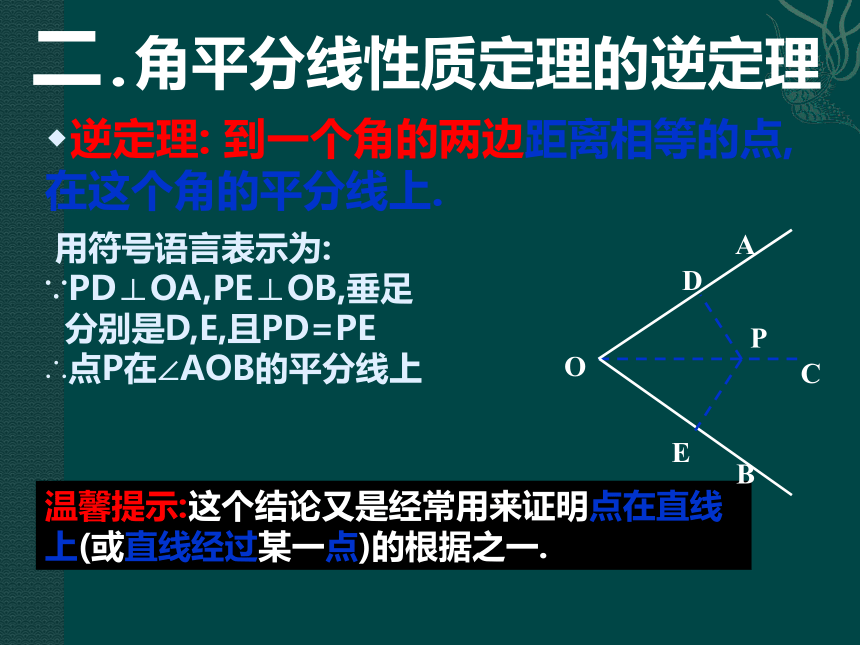
求证:点P在∠AOB的平分线上.分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠AOC=∠BOC.OCBAPDE逆定理: 到一个角的两边距离相等的点,在这个角的平分线上. 用符号语言表示为:
∵PD⊥OA,PE⊥OB,垂足
分别是D,E,且PD=PE
∴点P在∠AOB的平分线上温馨提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.OCBAPDE二.角平分线性质定理的逆定理 1.角平分线的性质定理：
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
到一个角的两边的距离相等的点，在这个角平分线上。
4.角平分线的性质定理是证明角相等、线段相等的新途径.角平分线的逆定理是证明点在直线上(或直线经过某一点)的根据之一.3.性质定理和逆定理的关系
点在角平分线上 点到角两边的距离相等总结归纳基本应用填空：
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1＝∠2
　　　　　　　　　DC=DE到一个角的两边的距离相等的点，在这个角平分线上。在角平分线上的点到角的两边的距离相等例1.已知:如图,∠C=900,∠B=300,
AD是Rt△ABC的角平分线.
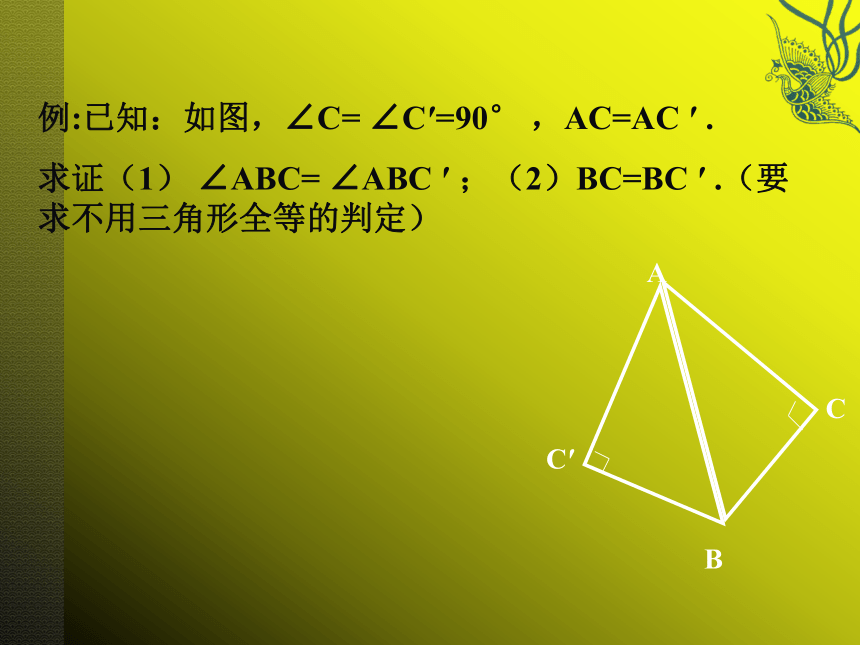
求证:BD＝2CD. 例:已知：如图，∠C= ∠C′=90° ，AC=AC ′ .
求证（1） ∠ABC= ∠ABC ′ ；（2）BC=BC ′ .（要求不用三角形全等的判定）B三.尺规作图角平分线的作法已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC
作法:用尺规作角的平分线.1.在OA和OB上分别截取OD,OE,使OD=OE.2.分别以点D和E为圆心,以大于DE/2长为
半径作弧,两弧在∠AOB内交于点C3.作射线OC.请你说明OC为什么
是∠AOB的平分线,
并与同桌进行交流.则射线OC就是∠AOB的平分线.１:如图，某个居民小区C附近有三条两两相交的道路MN、OA、OB，拟在MN上建造一个大型超市，使得它到OA、OB的距离相等，请确定该超市的位置P。
小区CP实际应用2：若已知超市P到道路OA 的距离为600米， 求P到道路OB的距离。驶向胜利的彼岸三角形内角的角平分线剪一个三角形纸片通过折叠找出每个角的平分线.结论:三角形三个角的平分线相交于一点.老师期望:
你能写出规范的证明过程.你能证明这个命题吗?观察这三条角平分线,你发现了什么?回味无穷一.定理 角平分线上的点到这个角的两边距离相等.
二.逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.三.遇到角平分线的问题,可以通过角平分线上的一点向角的两边引垂线,以便充分运用角平分线定理思考题：2、若要在△MON内部全部覆盖绿化，已知△MON的周长为2000米，∠OMN、∠MON的平分线交于点O，OD⊥MN，垂足为D，且OD=2米
求： △MON的面积3.已知:如图,P是∠AOB平分线上的一点，
PC⊥OA,PD⊥OB,垂足分别C,D.
求证:(1)OC=OD;
(2)OP是CD的垂直平分线. 证明两角相等的方法：１．同角（或等角）的余角（补角）相等．
２．平行线的性质
３．对顶角相等．
４．全等三角形的对应角相等
５．等边对等角
６．角平分线的性质定理及其逆定理证明线段相等的方法：１．全等三角形的对应边相等．
２．角平分线的性质定理
３．等角对等边
４．等腰三角形的三线合一
５.垂直平分线的性质定理（练习）已知：△MON中，MP平分∠OMN，OP平分∠MON，且PD⊥MN，PE⊥ON，垂足分别为点D、E
求证：点P在∠MNO的平分线上挑战自我如图,在△ABC中,已知AC=BC,∠C=900,AD
是△ABC的角平分线,DE⊥AB,垂足为E.(1)如果CD＝4cm，AC的长(2)求证:AB＝AC＋CD.2.已知:如图,△ABC的外角∠CBD和∠BCE的
角平分线相交于点F.
求证:点F在∠DAE的平分线上.