第3课时5.2.2选择结构(无答案)
文档属性
| 名称 | 第3课时5.2.2选择结构(无答案) |  | |
| 格式 | rar | ||
| 文件大小 | 28.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-05 09:13:00 | ||
图片预览


文档简介
第3课时5.2 流程图
重点难点
重点:掌握选择结构的执行过程;用流程图表示顺序结构的算法。
难点:选择结构程序执行的过程;用多分支结构描述求解问题的算法。
【学习导航】
知识网络
学习要求
1.理解选择结构的执行过程
2.如何在流程图中用选择框表示选择结构
3.理解多分支选择结构的流程
【课堂互动】
自学评价
1.问题:
某铁路客运部门规定甲乙两地之间旅客托运行李的费用为
其中w(单位:Kg)为行李的重量。
计算费用c(单位:元)的算法可以用怎样的算法结构来表示?
【解析】为了计算行李的托运费用,应先判断行李的重量是否大于50Kg,然后再选用相应的公式进行计算。其算法为:
S1 输入行李的重量w;
S2 如果w≤50,那么,否则;
S3 输出行李重量w和运费c。
上述算法的流程图如下:
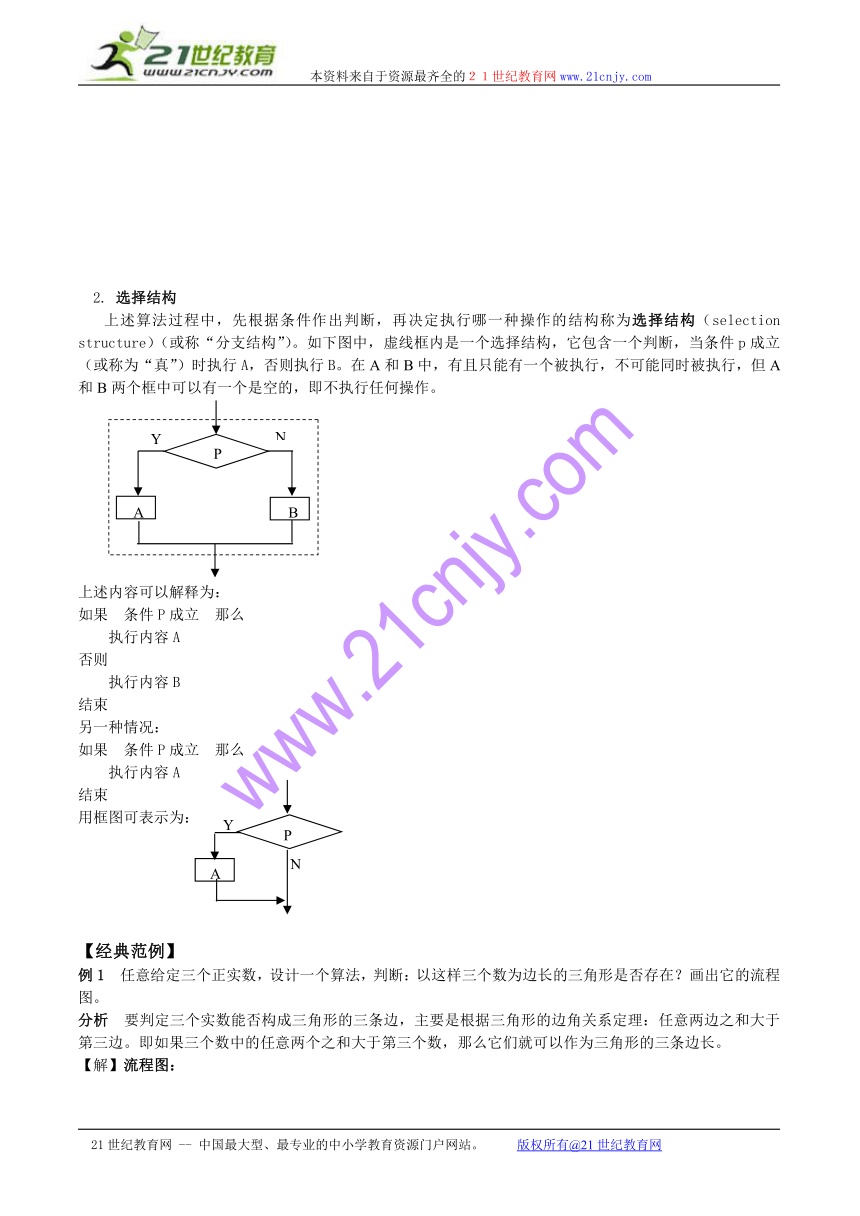
2. 选择结构
上述算法过程中,先根据条件作出判断,再决定执行哪一种操作的结构称为选择结构(selection structure)(或称“分支结构”)。如下图中,虚线框内是一个选择结构,它包含一个判断,当条件p成立(或称为“真”)时执行A,否则执行B。在A和B中,有且只能有一个被执行,不可能同时被执行,但A和B两个框中可以有一个是空的,即不执行任何操作。
上述内容可以解释为:
如果 条件P成立 那么
执行内容A
否则
执行内容B
结束
另一种情况:
如果 条件P成立 那么
执行内容A
结束
用框图可表示为:
【经典范例】
例1 任意给定三个正实数,设计一个算法,判断:以这样三个数为边长的三角形是否存在?画出它的流程图。
分析 要判定三个实数能否构成三角形的三条边,主要是根据三角形的边角关系定理:任意两边之和大于第三边。即如果三个数中的任意两个之和大于第三个数,那么它们就可以作为三角形的三条边长。
【解】流程图:
例2 设计求解一元二次方程
的一个算法,并用流程图表示。
【解】算法如下
S1 输入a,b,c
S2 △
S3 如果△<0,那么输出“由于方程无实数根”,否则,,输出这两个根。
流程图:
例3 如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法过程。
【解】
追踪训练一
1、如果考生的成绩 (以满分100分计) ,则输出“优秀”;若成绩,则输出“中等”;若,则输出“及格”;若,则输出“不及格”。若输入的成绩为95,则输出结果为______________。
2、下边的流程图(如图所示),能判断任意输入的数x的奇偶性,其中判断框内的条件是 .
3、下面的流程图表示了一个什么样的算法?
【解】
思考:如果要实现上述流程图所表示的目的,是否还有其它的算法?
算法:将a与b进行比较,将大的数放入一个临时变量Max中,再将Max与c比较,输出大的数。
4、写出解方程(a,b为常数)的算法,并画出流程图。
【解】算法如下:
流程图:
5、设计一个求任意实数的绝对值的算法,并画出流程图.
【解】算法如下:
S1 输入任意实数;
S2 若,则;否则;
S3 输出.
流程图如下:
开始
输入n
W≤50
Y
结束
N
输出w,c
N
Y
P
A
B
Y
P
N
A
开始
输入a,b,c
a>b且a>c
b>c
Y
N
Y
N
输出a
输出c
输出b
结束
开始
输入a,b
a=0
N
结束
Y
方程无解
重点难点
重点:掌握选择结构的执行过程;用流程图表示顺序结构的算法。
难点:选择结构程序执行的过程;用多分支结构描述求解问题的算法。
【学习导航】
知识网络
学习要求
1.理解选择结构的执行过程
2.如何在流程图中用选择框表示选择结构
3.理解多分支选择结构的流程
【课堂互动】
自学评价
1.问题:
某铁路客运部门规定甲乙两地之间旅客托运行李的费用为
其中w(单位:Kg)为行李的重量。
计算费用c(单位:元)的算法可以用怎样的算法结构来表示?
【解析】为了计算行李的托运费用,应先判断行李的重量是否大于50Kg,然后再选用相应的公式进行计算。其算法为:
S1 输入行李的重量w;
S2 如果w≤50,那么,否则;
S3 输出行李重量w和运费c。
上述算法的流程图如下:
2. 选择结构
上述算法过程中,先根据条件作出判断,再决定执行哪一种操作的结构称为选择结构(selection structure)(或称“分支结构”)。如下图中,虚线框内是一个选择结构,它包含一个判断,当条件p成立(或称为“真”)时执行A,否则执行B。在A和B中,有且只能有一个被执行,不可能同时被执行,但A和B两个框中可以有一个是空的,即不执行任何操作。
上述内容可以解释为:
如果 条件P成立 那么
执行内容A
否则
执行内容B
结束
另一种情况:
如果 条件P成立 那么
执行内容A
结束
用框图可表示为:
【经典范例】
例1 任意给定三个正实数,设计一个算法,判断:以这样三个数为边长的三角形是否存在?画出它的流程图。
分析 要判定三个实数能否构成三角形的三条边,主要是根据三角形的边角关系定理:任意两边之和大于第三边。即如果三个数中的任意两个之和大于第三个数,那么它们就可以作为三角形的三条边长。
【解】流程图:
例2 设计求解一元二次方程
的一个算法,并用流程图表示。
【解】算法如下
S1 输入a,b,c
S2 △
S3 如果△<0,那么输出“由于方程无实数根”,否则,,输出这两个根。
流程图:
例3 如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法过程。
【解】
追踪训练一
1、如果考生的成绩 (以满分100分计) ,则输出“优秀”;若成绩,则输出“中等”;若,则输出“及格”;若,则输出“不及格”。若输入的成绩为95,则输出结果为______________。
2、下边的流程图(如图所示),能判断任意输入的数x的奇偶性,其中判断框内的条件是 .
3、下面的流程图表示了一个什么样的算法?
【解】
思考:如果要实现上述流程图所表示的目的,是否还有其它的算法?
算法:将a与b进行比较,将大的数放入一个临时变量Max中,再将Max与c比较,输出大的数。
4、写出解方程(a,b为常数)的算法,并画出流程图。
【解】算法如下:
流程图:
5、设计一个求任意实数的绝对值的算法,并画出流程图.
【解】算法如下:
S1 输入任意实数;
S2 若,则;否则;
S3 输出.
流程图如下:
开始
输入n
W≤50
Y
结束
N
输出w,c
N
Y
P
A
B
Y
P
N
A
开始
输入a,b,c
a>b且a>c
b>c
Y
N
Y
N
输出a
输出c
输出b
结束
开始
输入a,b
a=0
N
结束
Y
方程无解
