第13课时5.4.3算法案例三(二分法)无答案
文档属性
| 名称 | 第13课时5.4.3算法案例三(二分法)无答案 |  | |
| 格式 | rar | ||
| 文件大小 | 88.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-05 09:13:00 | ||
图片预览

文档简介
第13课时 5.4 算法案例
重点难点
重点:理解区间二分法的意义,学会分析类似的问题;通过案例分析,体会算法思想,
难点:理解二分法的算法思想和算法表示
学习要求
1.理解区间二分法的意义,二分法主要是采用了循环结构处理问题要会分析类似的问题;
2.能由流程图分析出期所含有的结构并用为代码表示出相应的算法.
3.GoTo语句的认识及其他语句的进一步熟悉
【课堂互动】
问题:用区间二分法写出方程在区间[1,1.5]内的一个近似解(误差不超过0.001)的一个算法。
【算法设计思想】
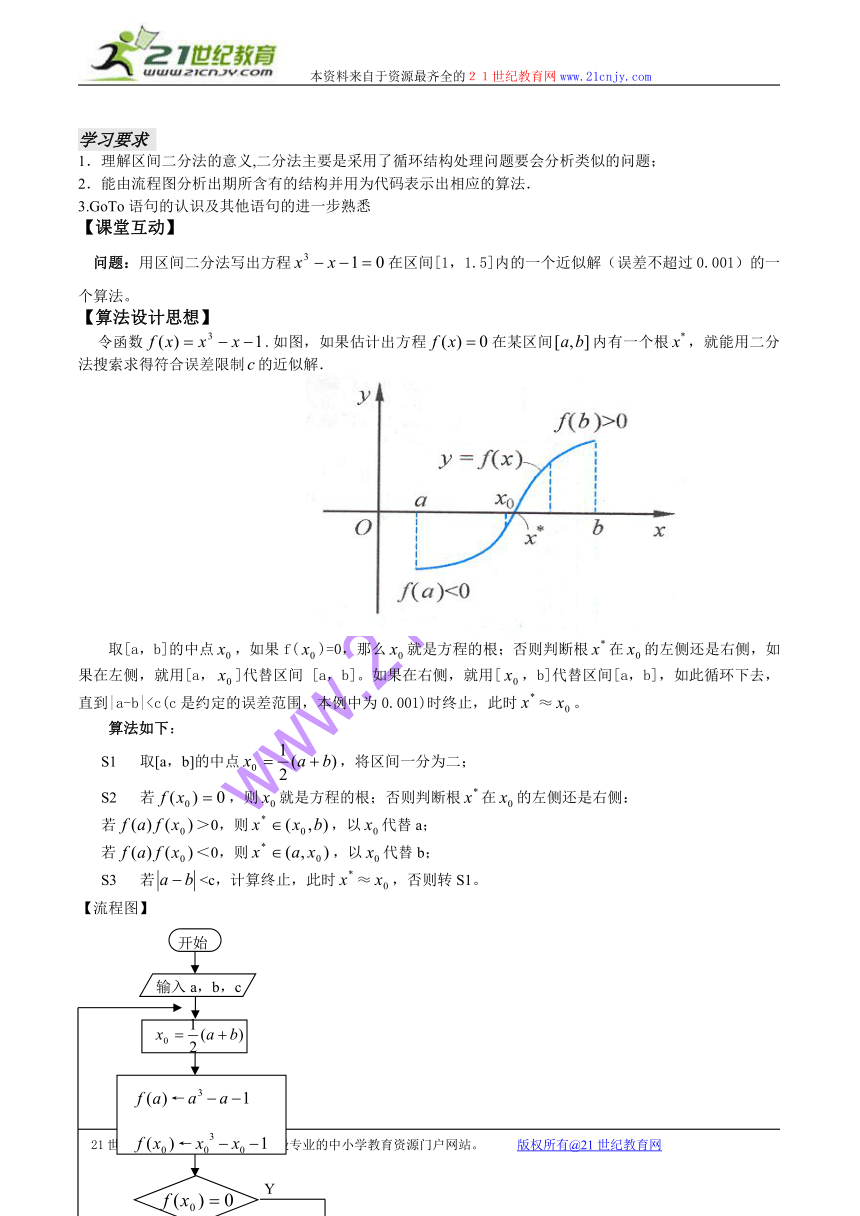
令函数.如图,如果估计出方程在某区间内有一个根,就能用二分法搜索求得符合误差限制的近似解.
取[a,b]的中点,如果f()=0,那么就是方程的根;否则判断根在的左侧还是右侧,如果在左侧,就用[a,]代替区间 [a,b]。如果在右侧,就用[,b]代替区间[a,b],如此循环下去,直到|a-b|算法如下:
S1 取[a,b]的中点,将区间一分为二;
S2 若,则就是方程的根;否则判断根在的左侧还是右侧:
若>0,则,以代替a;
若<0,则,以代替b;
S3 若【流程图】
代码1:
Read a,b,c
While And
If <0
Else
End If
End While
Print
代码2:
10 Read
20
30
40
50 If Then GoTo 120
60 If Then
70
80 Else
90
100 End If
110 If Then GoTo 20
120 Print
【追踪训练】
1.在直角坐标系中作出函数和的图象,根据图象判断方程的解的范围,再用二分法求这个方程的近似解(误差不超过0.001),并写出这个算法的伪代码,画出流程图。
【解】由图像可知方程有一个根在[1,2]内。
a←1
b←2
c←0.001
While ≥c
←(a+b)/2
←
←
If =0 Then Exit While
If <0 Then
b←
Else
a←
End If
End While
Print
流程图如下:
<0
开始
Y
结束
输入a,b,c
←
←
输出
a←
b←
N
Y
N
Y
N
重点难点
重点:理解区间二分法的意义,学会分析类似的问题;通过案例分析,体会算法思想,
难点:理解二分法的算法思想和算法表示
学习要求
1.理解区间二分法的意义,二分法主要是采用了循环结构处理问题要会分析类似的问题;
2.能由流程图分析出期所含有的结构并用为代码表示出相应的算法.
3.GoTo语句的认识及其他语句的进一步熟悉
【课堂互动】
问题:用区间二分法写出方程在区间[1,1.5]内的一个近似解(误差不超过0.001)的一个算法。
【算法设计思想】
令函数.如图,如果估计出方程在某区间内有一个根,就能用二分法搜索求得符合误差限制的近似解.
取[a,b]的中点,如果f()=0,那么就是方程的根;否则判断根在的左侧还是右侧,如果在左侧,就用[a,]代替区间 [a,b]。如果在右侧,就用[,b]代替区间[a,b],如此循环下去,直到|a-b|
S1 取[a,b]的中点,将区间一分为二;
S2 若,则就是方程的根;否则判断根在的左侧还是右侧:
若>0,则,以代替a;
若<0,则,以代替b;
S3 若
代码1:
Read a,b,c
While And
If <0
Else
End If
End While
代码2:
10 Read
20
30
40
50 If Then GoTo 120
60 If Then
70
80 Else
90
100 End If
110 If Then GoTo 20
120 Print
【追踪训练】
1.在直角坐标系中作出函数和的图象,根据图象判断方程的解的范围,再用二分法求这个方程的近似解(误差不超过0.001),并写出这个算法的伪代码,画出流程图。
【解】由图像可知方程有一个根在[1,2]内。
a←1
b←2
c←0.001
While ≥c
←(a+b)/2
←
←
If =0 Then Exit While
If <0 Then
b←
Else
a←
End If
End While
流程图如下:
<0
开始
Y
结束
输入a,b,c
←
←
输出
a←
b←
Y
N
Y
N
