第30课时7.1.1随机现象(无答案)
文档属性
| 名称 | 第30课时7.1.1随机现象(无答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 24.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-05 09:13:00 | ||
图片预览


文档简介
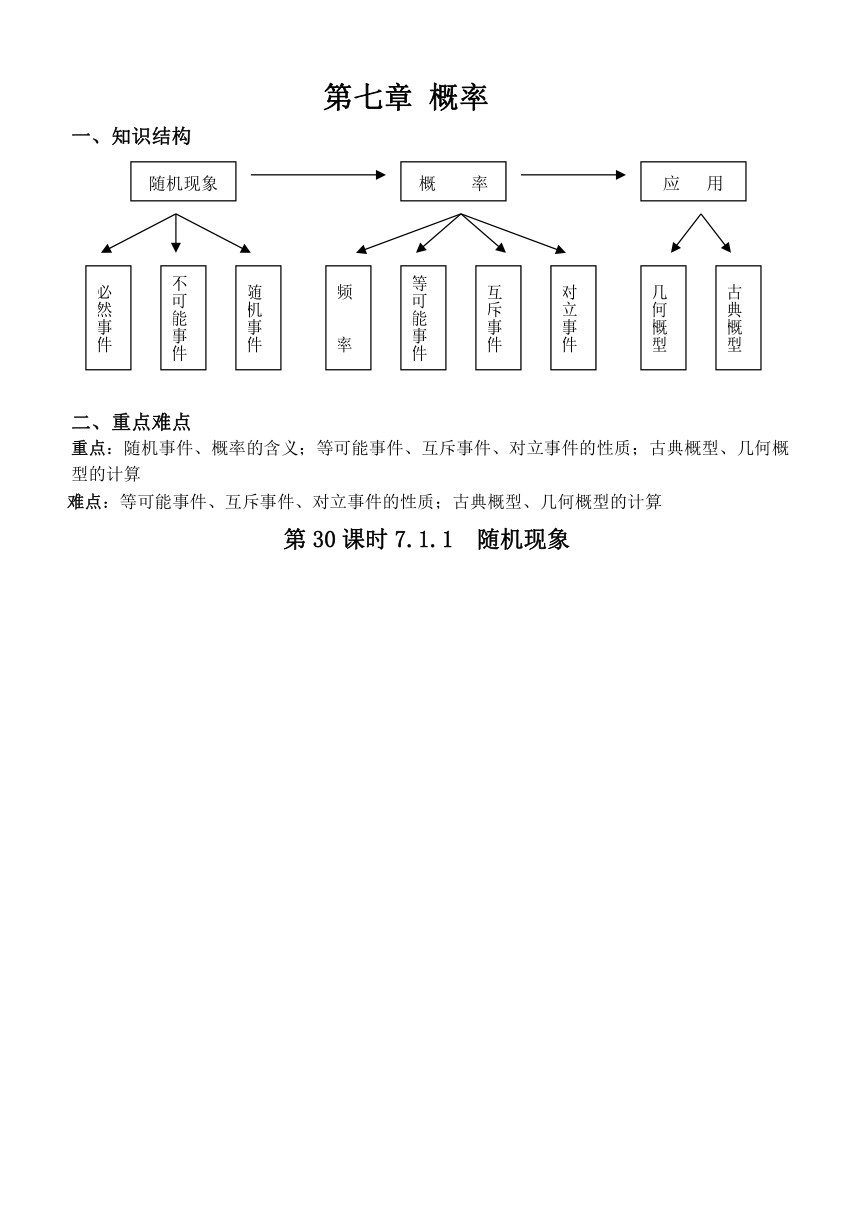
第七章 概率
一、知识结构
二、重点难点
重点:随机事件、概率的含义;等可能事件、互斥事件、对立事件的性质;古典概型、几何概型的计算
难点:等可能事件、互斥事件、对立事件的性质;古典概型、几何概型的计算
第30课时7.1.1 随机现象
【学习导航】
知识网络
学习要求
1.通过实例理解确定性现象与随机现象的含义和随机事件、必然事件、不可能事件的概念及其意义;
2.根据定义判断给定事件的类型,明确事件发生的条件是判断事件的类型的关键;
【课堂互动】
自学评价
1、
,这种现象叫做确定性现象
2、
,
这种现象叫做随机现象
3、 叫做必然事件;
叫做不可能事件;
叫做随机事件
【经典范例】
例1 观察下列现象:
(1)在标准大气压下水加热到1000C,沸腾;
(2)导体通电,发热;
(3)同性电荷,相互吸引;
(4)实心铁块丢人水中,铁块浮起;
(5)买一张福利彩票,中奖;
(6)掷一枚硬币,正面朝上;
其中是随机现象的有
【解】
例2 判断下列事件哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)抛掷一块石子,下落;.
(2)在标准大气压下且温度低于0℃时,冰
融化;
(3)某人射击一次,中靶;
(4)如果,那么;
(5)掷两枚硬币,均出现反面;
(6)抛掷两枚骰子,点数之和为15;
(7)从分别标有号数1,2,3,4,5的5张
标签中任取一张,得到4号签;
(8)某电话机在1分钟内收到2次呼叫;
(9)绿叶植物,不会光合作用;
(10)在常温下,焊锡熔化;
(11)若为实数,则;
(12)某人开车通过十个路口,都遇到绿灯;
其中必然事件有 ;不可能事件有 ;随机事件有
【解】
例3 在10个学生中,男生有个,现从10个学生中任选6人去参加某项活动.①至少有一个女生;②5个男生,1个女生;③3个男生,3个女生.当为何值时,使得①为必然事件,②为不可能事件,③为随机事件
【解】
例4 已知,给出事件.
(1)当A为必然事件时,求的取值范围;
(2)当A为不可能事件时,求的取值范围.
【解】
追踪训练
1.下列事件中随机事件的个数为 ( )
(1) 物体在重力作用下自由下落。
(2) 方程有两个不相等的实根
(3) 下周日下雨
(4) 某剧院明天的上座率不低于60%
A、1 B、2 C、3 D、4
2.下列试验中可以构成事件的是 ( )
A、掷一次硬币
B、射击一次
C、标准大气压下,水烧至100 0C
D、摸彩票中头奖
3.传说古时候有一个农夫正在田间干活,忽然发现一只兔子撞死在地头的木桩上,他喜出望外,于是拾起兔子回家了,第二天他就蹲在木桩旁守侯,就这样日复一日,年复一年,但再也没有等着被木桩碰死的兔子,这是为什么
4.事件”某人掷骰子5次,两次点数为2”是随机事件吗 条件和结果是什么 一次试验是指什么 一共做了几次试验
随机现象
概 率
应 用
必然事件
不可能事件
随机事件
频 率
等可能事件
互斥事件
对立事件
几何概型
古典概型
一、知识结构
二、重点难点
重点:随机事件、概率的含义;等可能事件、互斥事件、对立事件的性质;古典概型、几何概型的计算
难点:等可能事件、互斥事件、对立事件的性质;古典概型、几何概型的计算
第30课时7.1.1 随机现象
【学习导航】
知识网络
学习要求
1.通过实例理解确定性现象与随机现象的含义和随机事件、必然事件、不可能事件的概念及其意义;
2.根据定义判断给定事件的类型,明确事件发生的条件是判断事件的类型的关键;
【课堂互动】
自学评价
1、
,这种现象叫做确定性现象
2、
,
这种现象叫做随机现象
3、 叫做必然事件;
叫做不可能事件;
叫做随机事件
【经典范例】
例1 观察下列现象:
(1)在标准大气压下水加热到1000C,沸腾;
(2)导体通电,发热;
(3)同性电荷,相互吸引;
(4)实心铁块丢人水中,铁块浮起;
(5)买一张福利彩票,中奖;
(6)掷一枚硬币,正面朝上;
其中是随机现象的有
【解】
例2 判断下列事件哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)抛掷一块石子,下落;.
(2)在标准大气压下且温度低于0℃时,冰
融化;
(3)某人射击一次,中靶;
(4)如果,那么;
(5)掷两枚硬币,均出现反面;
(6)抛掷两枚骰子,点数之和为15;
(7)从分别标有号数1,2,3,4,5的5张
标签中任取一张,得到4号签;
(8)某电话机在1分钟内收到2次呼叫;
(9)绿叶植物,不会光合作用;
(10)在常温下,焊锡熔化;
(11)若为实数,则;
(12)某人开车通过十个路口,都遇到绿灯;
其中必然事件有 ;不可能事件有 ;随机事件有
【解】
例3 在10个学生中,男生有个,现从10个学生中任选6人去参加某项活动.①至少有一个女生;②5个男生,1个女生;③3个男生,3个女生.当为何值时,使得①为必然事件,②为不可能事件,③为随机事件
【解】
例4 已知,给出事件.
(1)当A为必然事件时,求的取值范围;
(2)当A为不可能事件时,求的取值范围.
【解】
追踪训练
1.下列事件中随机事件的个数为 ( )
(1) 物体在重力作用下自由下落。
(2) 方程有两个不相等的实根
(3) 下周日下雨
(4) 某剧院明天的上座率不低于60%
A、1 B、2 C、3 D、4
2.下列试验中可以构成事件的是 ( )
A、掷一次硬币
B、射击一次
C、标准大气压下,水烧至100 0C
D、摸彩票中头奖
3.传说古时候有一个农夫正在田间干活,忽然发现一只兔子撞死在地头的木桩上,他喜出望外,于是拾起兔子回家了,第二天他就蹲在木桩旁守侯,就这样日复一日,年复一年,但再也没有等着被木桩碰死的兔子,这是为什么
4.事件”某人掷骰子5次,两次点数为2”是随机事件吗 条件和结果是什么 一次试验是指什么 一共做了几次试验
随机现象
概 率
应 用
必然事件
不可能事件
随机事件
频 率
等可能事件
互斥事件
对立事件
几何概型
古典概型
