轴对称
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第一节 生活中的轴对称
日期 姓名
知识要点
1.轴对称图形和轴对称
(1)如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
(2)有的轴对称图形的对称轴不止一条,如圆就有无数条对称轴.
(3)有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.
(4)图形轴对称的性质:如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(5)轴对称是指两个图形之间的形状与位置关系,成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.
2.线段的垂直平分线
(1)经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线).
(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点在这条线段的垂直平分线上.因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.
典型例题
例:如图,点D是△ABC中∠BAC的平分线和边BC的垂直平分线DE的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H,求证BG=CH.
分析:由AD平分∠BAC及DG⊥AB、DH⊥AC可以得到DG=DH(角平分线的性质),而DE是BC的垂直平分线,由线段垂直平分线的性质可得到BD=CD,于是可利用“HL”证明Rt△BDG≌Rt△CDH得到BG=CH.
证明:连接BD、CD ∵点D在∠BAC的平分线上,又DG⊥AB、DH⊥AC;
∴DG=DH(角的平分线上的点到角的两边的距离相等)
∵DE是BC的垂直平分线
∴DB=DC(线段的垂直平分线上的点与这条线段两个端点的距离相等)
∵DG⊥AB、DH⊥AC ∴∠BGD=∠CHD=90°
在Rt△BDG和Rt△CDH中,
∴Rt△BDG≌Rt△CDH(HL) ∴BG=CH(全等三角形的对应边相等)
【典型例题】
一、选择题
1.下列说法错误的是 ( )
A.关于某条直线对称的两个三角形一定全等; B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称; D.角是关于它的平分线对称的图形
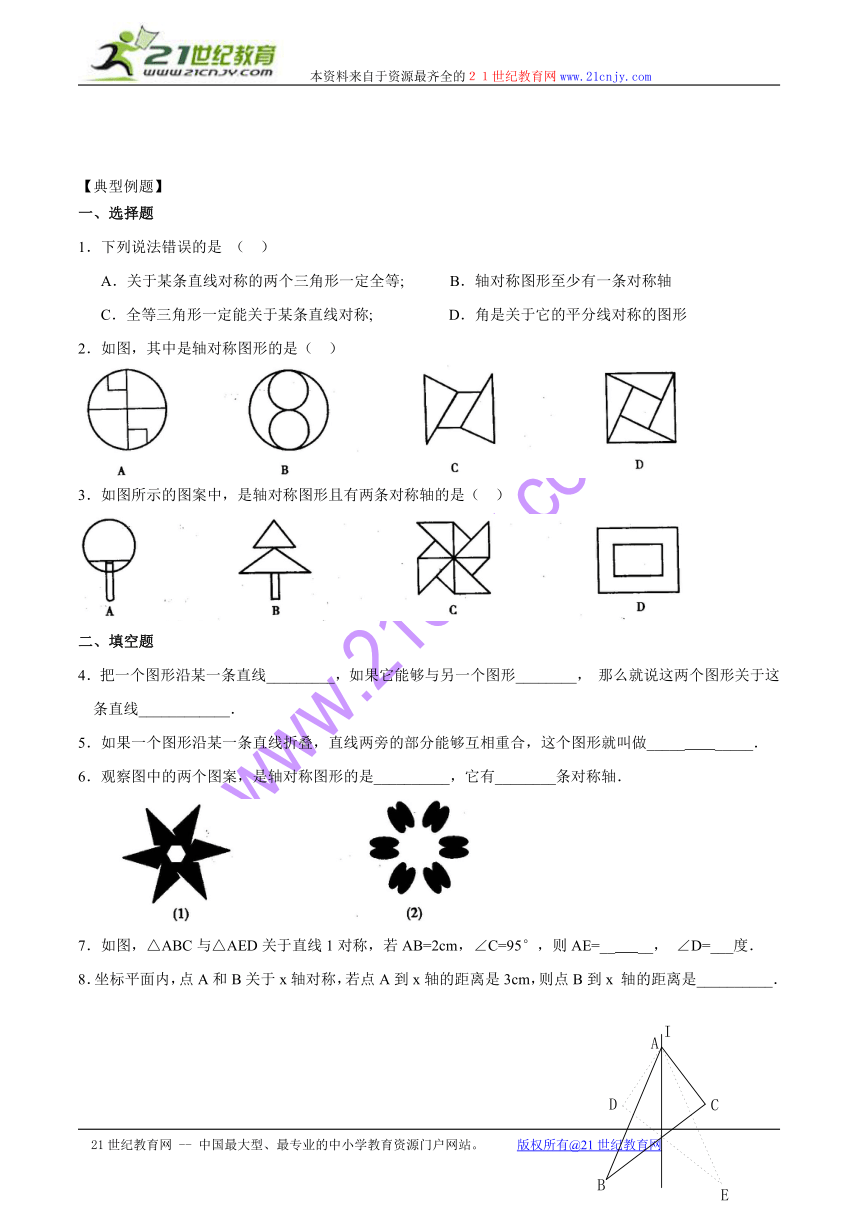
2.如图,其中是轴对称图形的是( )
3.如图所示的图案中,是轴对称图形且有两条对称轴的是( )
二、填空题
4.把一个图形沿某一条直线_________,如果它能够与另一个图形________,那么就说这两个图形关于这条直线____________.
5.如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做_____ _____.
6.观察图中的两个图案,是轴对称图形的是__________,它有________条对称轴.
7.如图,△ABC与△AED关于直线1对称,若AB=2cm,∠C=95°,则AE=__ __,∠D=___度.
8.坐标平面内,点A和B关于x轴对称,若点A到x轴的距离是3cm,则点B到x轴的距离是__________.
三、解答题
9.上图中的图形都是轴对称图形,请你试着画出它们的对称轴.
10.如图,△ABC与△ADE关于直线MN对称.BC与DE的交点F在直线MN上.①指出两个三角形中的对称点;②指出图中相等的线段和角;③图中还有对称的三角形吗?
四、探究题
11.如图,把一张纸片对折后,用笔尖在纸上扎出图(3)所示的图案,将纸打开后铺平,观察你所得的图案.位于折痕两侧的部分有什么关系?
随堂小测
一、选择题
1.点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A.PA=PB B.PA=PC C.PB=PC D.点P到∠ACB的两边的距离相等
2.下列说法错误的是( )
A.D、E是线段AB的垂直平分线上的两点,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是线段AB的垂直平分线
3.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边垂直平分线的交点
4.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是( )
A.9 B.8 C.7 D.6
5.平面内到不在同一条直线的三个点A、B、C的距离相等的点有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
6.经过线段的____________ _______的直线,叫做这条线段的垂直平分线.
7.线段的垂直平分线上的点_________ ______________________;反过来,与一条线段两个端点距离相等的点在这条线段的____________________上,因此线段的垂直平分线可以看成___________________ 的集合.
8.线段是轴对称图形,它的对称轴是__________________ __.
9.如下图,△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,则BC=_________.
10.如右图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC=_________.
三、解答题:
11.△ABC中,边AB、AC的垂直平分线交于点P,求证:点P在BC的垂直平分线上.
12.如右图,直线AD是线段BC的垂直平分线,求证:∠ABD=∠ACD.
四、探究题
13.如图,△ABC中∠ACB=90°,AD平分∠BAC,DE⊥AB于E,求证:直线AD是CE的垂直平分线.
课后作业
一、选择题
1.如图所示的标志中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.如图是用纸折叠成的图案,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图1,先将纸折叠,然后再剪,展开即得到图案):图2中的四个图案,不能用上述方法剪出的是( )
(1)
二、填空题:
4.轴对称图形中任意一组对应点的连线段的__________________是该图形的对称轴.
5.如果两个图形关于某条直线对称,那么对称轴是对应点连线的__________.
6.角是轴对称图形,其对称轴是________________________所在的直线.
7.平面内两点A、B关于____________________________对称.
三、解答题:
8.如图,已知△ABC,请用直尺与圆规作图,将三角形的面积两等分.(不写作法,但要保留作图痕迹)
9.已知图中的图形都是轴对称图形,请你画出它们的对称轴.
10.如图,已知点M、N和∠AOB,求作一点P,使P到点M、N的距离相等,
且到∠AOB的两边的距离相等.
四、探究题
11.如图,△ABC和△A′B′C′关于直线m对称.
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其它对应线段(或其延长线)的交点呢?你发现了什么规律.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第一节 生活中的轴对称
日期 姓名
知识要点
1.轴对称图形和轴对称
(1)如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
(2)有的轴对称图形的对称轴不止一条,如圆就有无数条对称轴.
(3)有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.
(4)图形轴对称的性质:如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(5)轴对称是指两个图形之间的形状与位置关系,成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.
2.线段的垂直平分线
(1)经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线).
(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点在这条线段的垂直平分线上.因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.
典型例题
例:如图,点D是△ABC中∠BAC的平分线和边BC的垂直平分线DE的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H,求证BG=CH.
分析:由AD平分∠BAC及DG⊥AB、DH⊥AC可以得到DG=DH(角平分线的性质),而DE是BC的垂直平分线,由线段垂直平分线的性质可得到BD=CD,于是可利用“HL”证明Rt△BDG≌Rt△CDH得到BG=CH.
证明:连接BD、CD ∵点D在∠BAC的平分线上,又DG⊥AB、DH⊥AC;
∴DG=DH(角的平分线上的点到角的两边的距离相等)
∵DE是BC的垂直平分线
∴DB=DC(线段的垂直平分线上的点与这条线段两个端点的距离相等)
∵DG⊥AB、DH⊥AC ∴∠BGD=∠CHD=90°
在Rt△BDG和Rt△CDH中,
∴Rt△BDG≌Rt△CDH(HL) ∴BG=CH(全等三角形的对应边相等)
【典型例题】
一、选择题
1.下列说法错误的是 ( )
A.关于某条直线对称的两个三角形一定全等; B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称; D.角是关于它的平分线对称的图形
2.如图,其中是轴对称图形的是( )
3.如图所示的图案中,是轴对称图形且有两条对称轴的是( )
二、填空题
4.把一个图形沿某一条直线_________,如果它能够与另一个图形________,那么就说这两个图形关于这条直线____________.
5.如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做_____ _____.
6.观察图中的两个图案,是轴对称图形的是__________,它有________条对称轴.
7.如图,△ABC与△AED关于直线1对称,若AB=2cm,∠C=95°,则AE=__ __,∠D=___度.
8.坐标平面内,点A和B关于x轴对称,若点A到x轴的距离是3cm,则点B到x轴的距离是__________.
三、解答题
9.上图中的图形都是轴对称图形,请你试着画出它们的对称轴.
10.如图,△ABC与△ADE关于直线MN对称.BC与DE的交点F在直线MN上.①指出两个三角形中的对称点;②指出图中相等的线段和角;③图中还有对称的三角形吗?
四、探究题
11.如图,把一张纸片对折后,用笔尖在纸上扎出图(3)所示的图案,将纸打开后铺平,观察你所得的图案.位于折痕两侧的部分有什么关系?
随堂小测
一、选择题
1.点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A.PA=PB B.PA=PC C.PB=PC D.点P到∠ACB的两边的距离相等
2.下列说法错误的是( )
A.D、E是线段AB的垂直平分线上的两点,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是线段AB的垂直平分线
3.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边垂直平分线的交点
4.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是( )
A.9 B.8 C.7 D.6
5.平面内到不在同一条直线的三个点A、B、C的距离相等的点有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
6.经过线段的____________ _______的直线,叫做这条线段的垂直平分线.
7.线段的垂直平分线上的点_________ ______________________;反过来,与一条线段两个端点距离相等的点在这条线段的____________________上,因此线段的垂直平分线可以看成___________________ 的集合.
8.线段是轴对称图形,它的对称轴是__________________ __.
9.如下图,△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,则BC=_________.
10.如右图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC=_________.
三、解答题:
11.△ABC中,边AB、AC的垂直平分线交于点P,求证:点P在BC的垂直平分线上.
12.如右图,直线AD是线段BC的垂直平分线,求证:∠ABD=∠ACD.
四、探究题
13.如图,△ABC中∠ACB=90°,AD平分∠BAC,DE⊥AB于E,求证:直线AD是CE的垂直平分线.
课后作业
一、选择题
1.如图所示的标志中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.如图是用纸折叠成的图案,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图1,先将纸折叠,然后再剪,展开即得到图案):图2中的四个图案,不能用上述方法剪出的是( )
(1)
二、填空题:
4.轴对称图形中任意一组对应点的连线段的__________________是该图形的对称轴.
5.如果两个图形关于某条直线对称,那么对称轴是对应点连线的__________.
6.角是轴对称图形,其对称轴是________________________所在的直线.
7.平面内两点A、B关于____________________________对称.
三、解答题:
8.如图,已知△ABC,请用直尺与圆规作图,将三角形的面积两等分.(不写作法,但要保留作图痕迹)
9.已知图中的图形都是轴对称图形,请你画出它们的对称轴.
10.如图,已知点M、N和∠AOB,求作一点P,使P到点M、N的距离相等,
且到∠AOB的两边的距离相等.
四、探究题
11.如图,△ABC和△A′B′C′关于直线m对称.
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其它对应线段(或其延长线)的交点呢?你发现了什么规律.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
