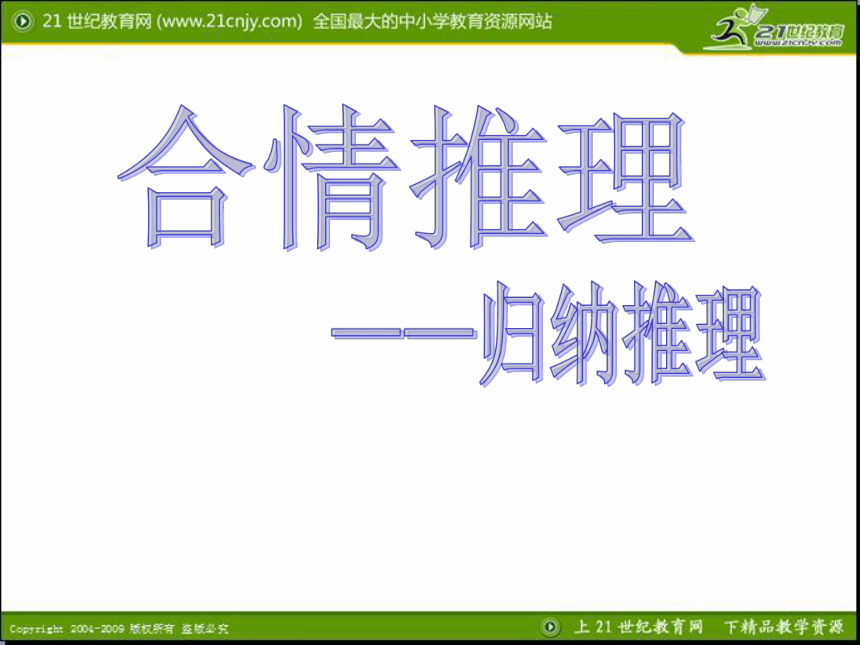
新课标人教a版选修2-2第二章推理与证明2.1合情推理与演绎推理
文档属性
| 名称 | 新课标人教a版选修2-2第二章推理与证明2.1合情推理与演绎推理 |
|
|
| 格式 | rar | ||
| 文件大小 | 867.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-06 00:00:00 | ||
图片预览





文档简介
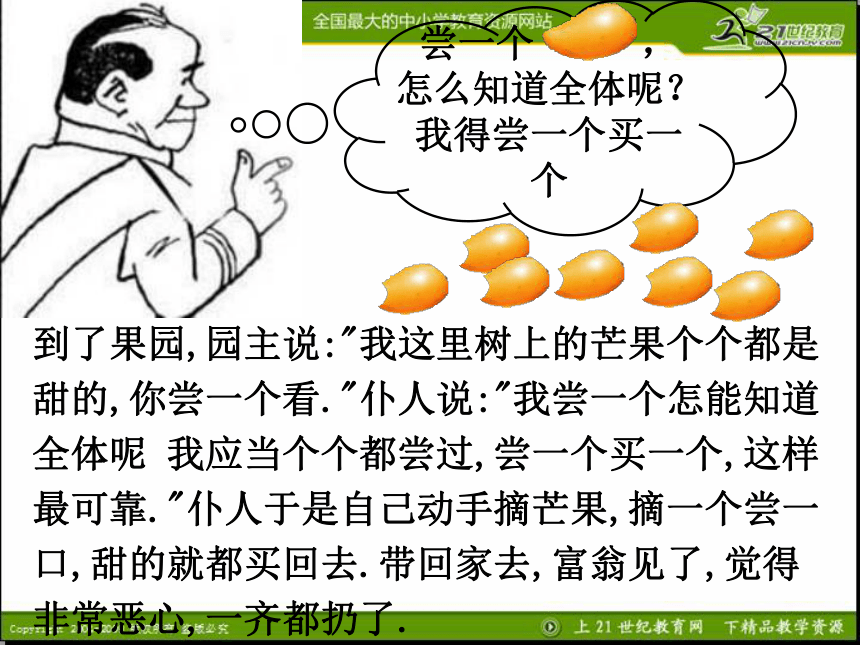
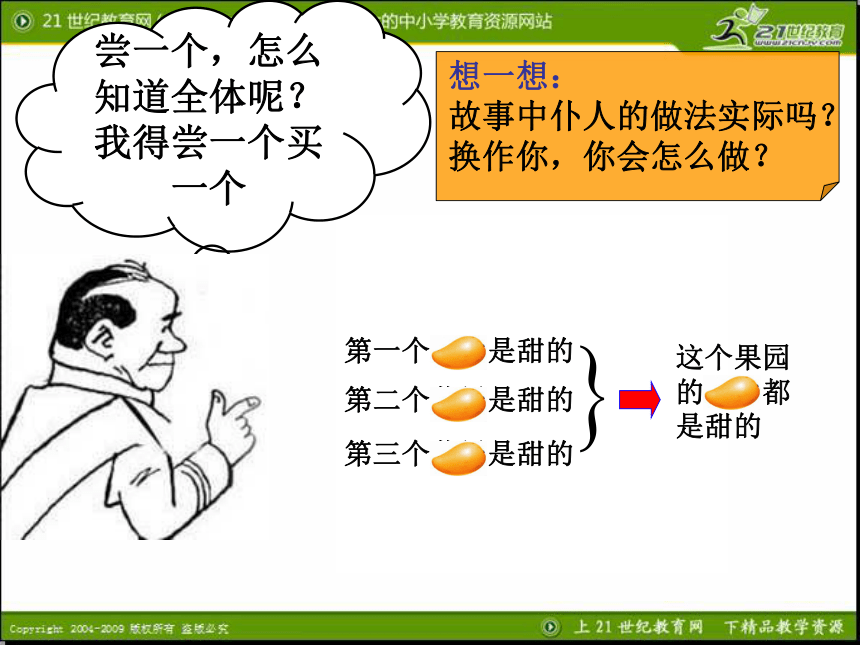
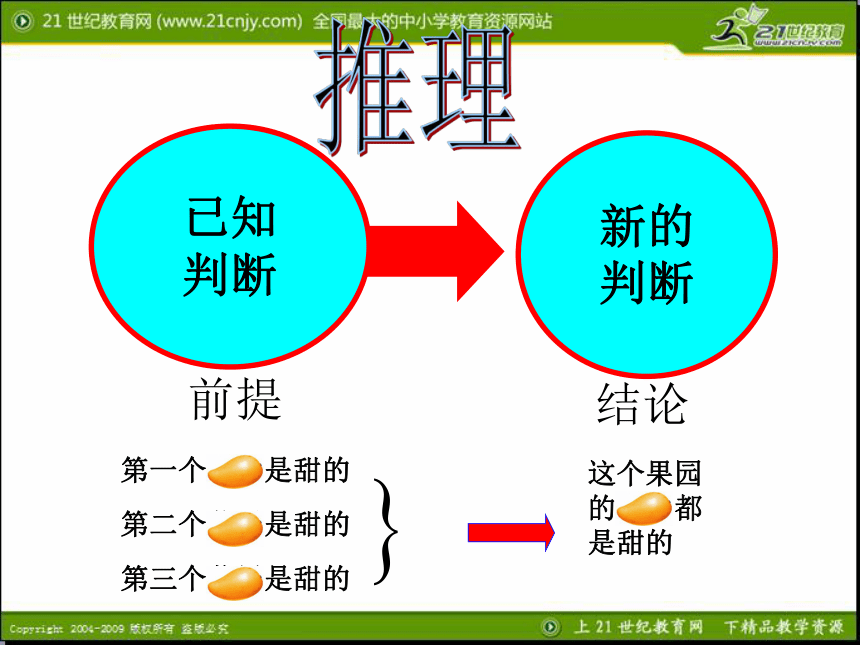
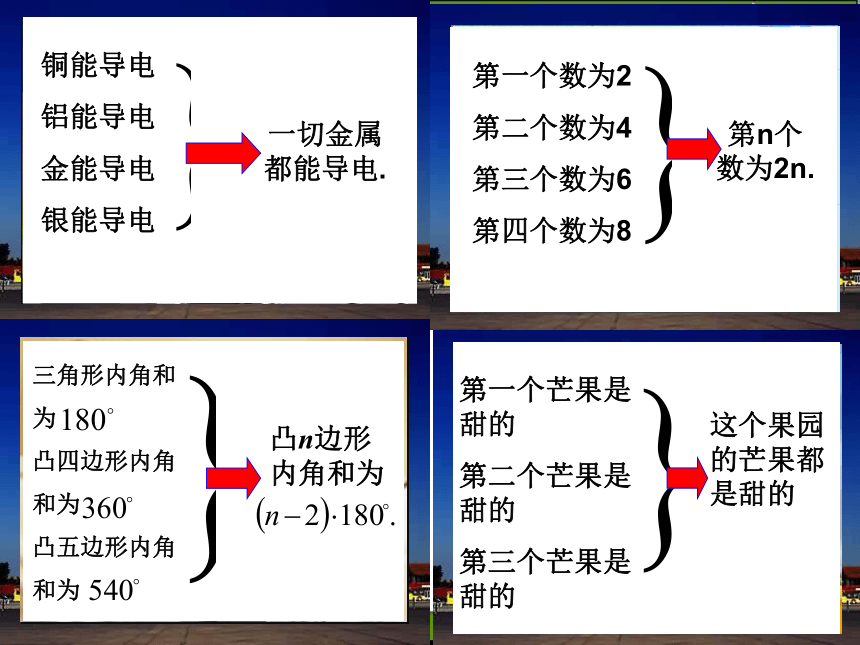
课件34张PPT。合情推理——归纳推理要甜的,好吃的! 从前有一位富翁想吃芒果,打发他的仆人到果园去买,并告诉他:"要甜的,好吃的,你才买."仆人拿好钱就去了.到了果园,园主说:"我这里树上的芒果个个都是甜的,你尝一个看."仆人说:"我尝一个怎能知道全体呢 我应当个个都尝过,尝一个买一个,这样最可靠."仆人于是自己动手摘芒果,摘一个尝一口,甜的就都买回去.带回家去,富翁见了,觉得非常恶心,一齐都扔了.尝一个 ,怎么知道全体呢?我得尝一个买一个尝一个,怎么知道全体呢?我得尝一个买一个第一个芒果是甜的第二个芒果是甜的第三个芒果是甜的这个果园的芒果都是甜的推理第一个芒果是甜的第二个芒果是甜的第三个芒果是甜的这个果园的芒果都是甜的铜能导电
铝能导电
金能导电
银能导电三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
第一个芒果是甜的
第二个芒果是甜的
第三个芒果是甜的第一个数为2
第二个数为4
第三个数为6
第四个数为8
铜能导电
铝能导电
金能导电
银能导电三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
第一个芒果是甜的
第二个芒果是甜的
第三个芒果是甜的第一个数为2
第二个数为4
第三个数为6
第四个数为8
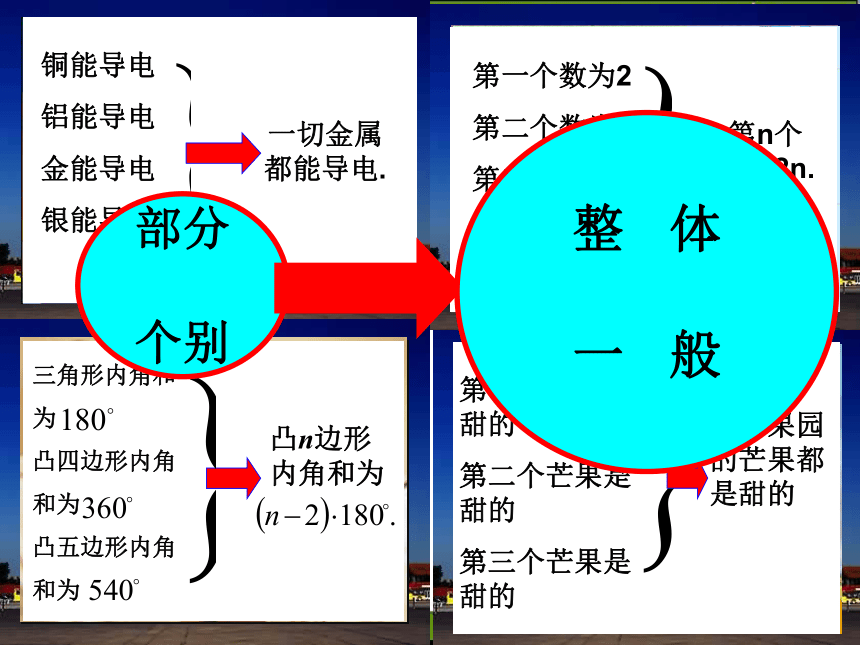
部分
个别整 体
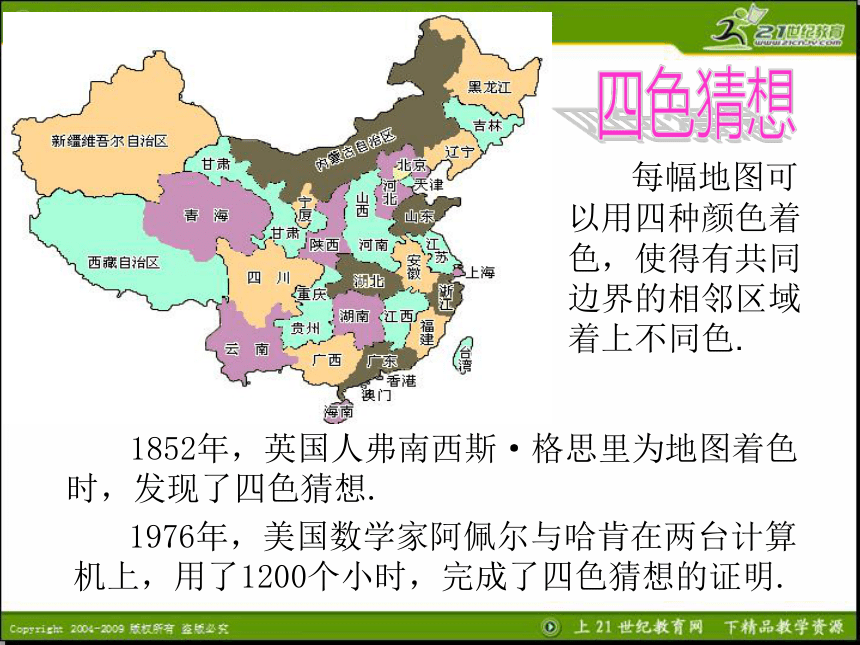
一 般归纳推理 由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征,或者由个别事实概括出一般性的结论,这样的推理称为归纳推理(简称归纳).浙江省地图 每幅地图可以用四种颜色着色,使得有共同边界的相邻区域着上不同色. 四色猜想 1852年,英国人弗南西斯·格思里为地图着色时,发现了四色猜想. 1976年,美国数学家阿佩尔与哈肯在两台计算机上,用了1200个小时,完成了四色猜想的证明.
任何一个不小于6的偶数都等于两个奇质数的和.观察下列等式
6 = 3 + 3
8 = 3 + 5
10= 3 + 7
12= 5 + 7归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.大胆猜想:陈氏定理哥德巴赫猜想16 = 5+11
18 = 7+11
20 = 7+13
22 = 5+17 半个世纪之后,欧拉发现:猜想:观察分析发现规律
大胆猜想检验猜想归纳推理的一般步骤费马猜想(05年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数.探究2当n ≥3 时, f(n)= .(用n表示)感
悟
交
流作 业 完成课本 P83 A组 1—3选做:如右图三角阵, 从上往下数,第1次全行的数都为1的是第1行,第2次全行的数为1的是第3行,…,第n次全行的数都为1的是第 行;第61行中1的个数是 .
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
… …谢谢指导!2.由三角形内角和为 ,凸四边形内角和为 ,凸五边形内角和为 ,
1.由铜、铁、铝、金、银等金属都能导电,3.地球上有生命,火星具有一些与地球类
似的特征,
4.因为所有人都会死,苏格拉底是人,
猜想:一切金属都能导电.
猜想:凸n边形内角和为 猜想:火星上也有生命.所以苏格拉底会死.
归纳推理类比推理合情推理演绎推理推
理牛顿发现万有引力
门捷列夫发现元素周期律应用归纳推理可以
发现新事实,获得新结论!归纳推理是科学发现的重要途径!歌德巴赫猜想
四色定理例3(2004春季上海)根据图中5个图形及相应点的个数的变化规律,试猜测第n个图形中有 个点.(1)(2)(3)(4)(5) 合情推理是地球上
最美丽的思维花朵之一!探究1 任取两条平行线 ,在直线上 任取三个点依次记作 ,在直线 上任取三个点依次记作 .连接 ,记交点为 ;连接 ,记交点为 ;连接 ,记交点为 .你能发现什么规律呢?
例1 已知数列 的首项 ,且有(2)令 ,化简 .(1)求数列 的通项公式;2.由三角形内角和为 ,凸四边形内角和为 ,凸五边形内角和为 ,
1.由铜、铁、铝、金、银等金属都能导电,3.地球上有生命,火星具有一些与地球类
似的特征,
4.因为所有人都会死,苏格拉底是人,
推出一切金属都能导电.
推出凸n边形内角和为 推出火星上也有生命.所以苏格拉底会死.
归纳推理类比推理合情推理演绎推理推
理合情推理——归纳推理 某课题组为了解本市的高中生数学学习状态,对四所学校做了一个问卷调查,其中有两道题的统计数据如下: 根据这四所学校的情况,你能判断该市高中生对数学的普遍印象吗? 佛教《百喻经》中有这样一则故事。 从前有一位富翁想吃芒果,打发他的仆人到果园去买,并告诉他:"要甜的,好吃的,你才买."仆人拿好钱就去了.到了果园,园主说:"我这里树上的芒果个个都是甜的,你尝一个看."仆人说:"我尝一个怎能知道全体呢 我应当个个都尝过,尝一个买一个,这样最可靠."仆人于是自己动手摘芒果,摘一个尝一口,甜的就都买回去.带回家去,富翁见了,觉得非常恶心,一齐都扔了.第一个芒果是甜的第二个芒果是甜的第三个芒果是甜的这个果园的芒果都是甜的(05年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,f(4)= ,当n>4时,f(n)= .(用n表示)探究2
铝能导电
金能导电
银能导电三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
第一个芒果是甜的
第二个芒果是甜的
第三个芒果是甜的第一个数为2
第二个数为4
第三个数为6
第四个数为8
铜能导电
铝能导电
金能导电
银能导电三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
第一个芒果是甜的
第二个芒果是甜的
第三个芒果是甜的第一个数为2
第二个数为4
第三个数为6
第四个数为8
部分
个别整 体
一 般归纳推理 由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征,或者由个别事实概括出一般性的结论,这样的推理称为归纳推理(简称归纳).浙江省地图 每幅地图可以用四种颜色着色,使得有共同边界的相邻区域着上不同色. 四色猜想 1852年,英国人弗南西斯·格思里为地图着色时,发现了四色猜想. 1976年,美国数学家阿佩尔与哈肯在两台计算机上,用了1200个小时,完成了四色猜想的证明.
任何一个不小于6的偶数都等于两个奇质数的和.观察下列等式
6 = 3 + 3
8 = 3 + 5
10= 3 + 7
12= 5 + 7归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.大胆猜想:陈氏定理哥德巴赫猜想16 = 5+11
18 = 7+11
20 = 7+13
22 = 5+17 半个世纪之后,欧拉发现:猜想:观察分析发现规律
大胆猜想检验猜想归纳推理的一般步骤费马猜想(05年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数.探究2当n ≥3 时, f(n)= .(用n表示)感
悟
交
流作 业 完成课本 P83 A组 1—3选做:如右图三角阵, 从上往下数,第1次全行的数都为1的是第1行,第2次全行的数为1的是第3行,…,第n次全行的数都为1的是第 行;第61行中1的个数是 .
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
… …谢谢指导!2.由三角形内角和为 ,凸四边形内角和为 ,凸五边形内角和为 ,
1.由铜、铁、铝、金、银等金属都能导电,3.地球上有生命,火星具有一些与地球类
似的特征,
4.因为所有人都会死,苏格拉底是人,
猜想:一切金属都能导电.
猜想:凸n边形内角和为 猜想:火星上也有生命.所以苏格拉底会死.
归纳推理类比推理合情推理演绎推理推
理牛顿发现万有引力
门捷列夫发现元素周期律应用归纳推理可以
发现新事实,获得新结论!归纳推理是科学发现的重要途径!歌德巴赫猜想
四色定理例3(2004春季上海)根据图中5个图形及相应点的个数的变化规律,试猜测第n个图形中有 个点.(1)(2)(3)(4)(5) 合情推理是地球上
最美丽的思维花朵之一!探究1 任取两条平行线 ,在直线上 任取三个点依次记作 ,在直线 上任取三个点依次记作 .连接 ,记交点为 ;连接 ,记交点为 ;连接 ,记交点为 .你能发现什么规律呢?
例1 已知数列 的首项 ,且有(2)令 ,化简 .(1)求数列 的通项公式;2.由三角形内角和为 ,凸四边形内角和为 ,凸五边形内角和为 ,
1.由铜、铁、铝、金、银等金属都能导电,3.地球上有生命,火星具有一些与地球类
似的特征,
4.因为所有人都会死,苏格拉底是人,
推出一切金属都能导电.
推出凸n边形内角和为 推出火星上也有生命.所以苏格拉底会死.
归纳推理类比推理合情推理演绎推理推
理合情推理——归纳推理 某课题组为了解本市的高中生数学学习状态,对四所学校做了一个问卷调查,其中有两道题的统计数据如下: 根据这四所学校的情况,你能判断该市高中生对数学的普遍印象吗? 佛教《百喻经》中有这样一则故事。 从前有一位富翁想吃芒果,打发他的仆人到果园去买,并告诉他:"要甜的,好吃的,你才买."仆人拿好钱就去了.到了果园,园主说:"我这里树上的芒果个个都是甜的,你尝一个看."仆人说:"我尝一个怎能知道全体呢 我应当个个都尝过,尝一个买一个,这样最可靠."仆人于是自己动手摘芒果,摘一个尝一口,甜的就都买回去.带回家去,富翁见了,觉得非常恶心,一齐都扔了.第一个芒果是甜的第二个芒果是甜的第三个芒果是甜的这个果园的芒果都是甜的(05年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,f(4)= ,当n>4时,f(n)= .(用n表示)探究2
