新课标人教A版选修2-1第三章 空间向量与立体几何3.2立体几何中的向量方法之用向量方法求空间角和距离
文档属性
| 名称 | 新课标人教A版选修2-1第三章 空间向量与立体几何3.2立体几何中的向量方法之用向量方法求空间角和距离 |

|
|
| 格式 | rar | ||
| 文件大小 | 72.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-09 14:33:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
用向量方法求空间角和距离
教学目标:
1、掌握求空间角和距离的向量方法。
2、培养学生的新思维和解题能力。
教学重点与难点:
重点:用向量工具求空间角和距离的方法。
难点:理解向量有关基本知识点。
教学方法:探究法与讲授法相结合。
教学设计:
一、复习与导入:
先复习空间向量有关知识点,然后强调向量作为工具,可解决立体几何中很多疑难问题,从而导出新课。
二、新授:
先让学生自主探究选修2-1P102例2,然后学生之间讨论方法。最后老师和学生一起作如下总结:
1、求空间角问题
空间的角主要有:直线和平面所成的角;异面直线所成的角;二面角。
(1)、求线面角:
设是斜线l的方向向量,是平面的法向量,
则斜线l与平面所成的角=
(2)求异面直线所成的角:
设、分别为异面直线a、b的方向向量,
则两异面直线所成的角=
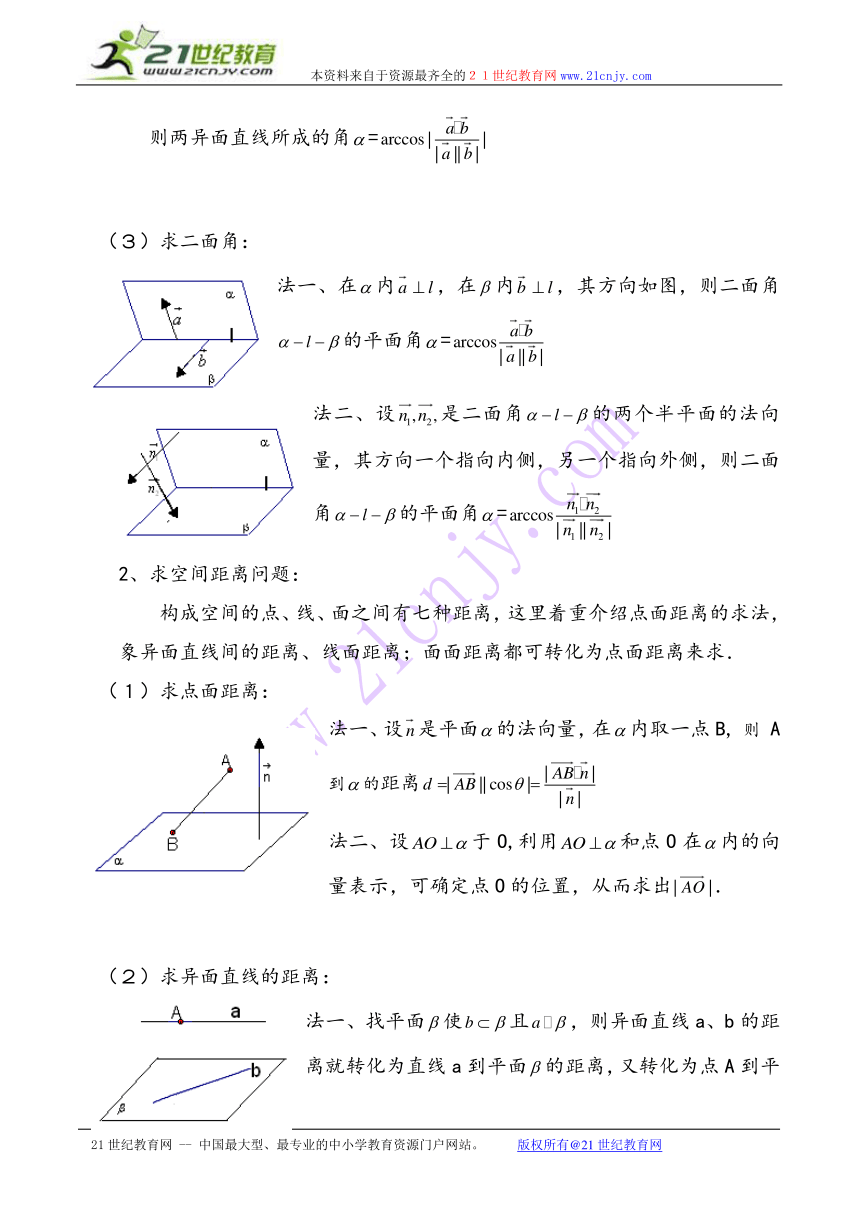
(3)求二面角:
法一、在内,在内,其方向如图,则二面角的平面角=
法二、设是二面角的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧,则二面角的平面角=
2、求空间距离问题:
构成空间的点、线、面之间有七种距离,这里着重介绍点面距离的求法,象异面直线间的距离、线面距离;面面距离都可转化为点面距离来求.
(1)求点面距离:
法一、设是平面的法向量,在内取一点B, 则 A到的距离
法二、设于O,利用和点O在内的向量表示,可确定点O的位置,从而求出.
(2)求异面直线的距离:
法一、找平面使且,则异面直线a、b的距离就转化为直线a到平面的距离,又转化为点A到平面的距离.
法二、在a上取一点A, 在b上取一点B, 设、分别为异面直线a、b的方向向量,求(,),则异面直线a、b的距离(此方法移植于点面距离的求法).
三、例题讲解:
例1.如图,在棱长为2的正方体中,E、F分别是棱的中点.
(Ⅰ)求异面直线所成的角;
(II)求和面EFBD所成的角;
(III)求到面EFBD的距离
解:略
设计说明:1.例1,首先选择以一个容易建立空间直角坐标系的多面体―――正方体为载体,来说明空间角和距离的向量求法易于学生理解.
2.解决(1)后,可让学生进一步求这两条异面直线的距离,并让学生体会一下:如果用传统方法恐怕很难(不必多讲,高中对公垂线的作法不作要求).
3.完成这3道小题后,总结:对于易建立空间直角坐标系的立几题,无论求角、距离还是证明平行、垂直(是前者的特殊情况),都可用向量方法来解决,
向量方法可以人人学会,它程序化,不需技巧.
例2.如图,三棱柱中,已知A BCD是边长为1的正方形,四边形
是矩形,
(Ⅰ)若=1,求直线AB到面的距离.
(II) 试问:当的长度为多少时,二面角
的大小为
解:(略)
设计说明:1.通过(Ⅰ),复习线面距离转化为点面距离再转化为一向量在一向量(法向量)投影的绝对值的解题思路与方法.
2.通过(II),复习面面角转化为两向量的夹角或其补角的方法,也可借此机会说明为什么这两个角相等或互补,就没有其他情况.
四、课堂练习:
P107练习题:1、2
五、小结:
与学生一同归纳小结本节课的重点知识点。(略)
六、作业布置:
课本习题、导航练习题。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
用向量方法求空间角和距离
教学目标:
1、掌握求空间角和距离的向量方法。
2、培养学生的新思维和解题能力。
教学重点与难点:
重点:用向量工具求空间角和距离的方法。
难点:理解向量有关基本知识点。
教学方法:探究法与讲授法相结合。
教学设计:
一、复习与导入:
先复习空间向量有关知识点,然后强调向量作为工具,可解决立体几何中很多疑难问题,从而导出新课。
二、新授:
先让学生自主探究选修2-1P102例2,然后学生之间讨论方法。最后老师和学生一起作如下总结:
1、求空间角问题
空间的角主要有:直线和平面所成的角;异面直线所成的角;二面角。
(1)、求线面角:
设是斜线l的方向向量,是平面的法向量,
则斜线l与平面所成的角=
(2)求异面直线所成的角:
设、分别为异面直线a、b的方向向量,
则两异面直线所成的角=
(3)求二面角:
法一、在内,在内,其方向如图,则二面角的平面角=
法二、设是二面角的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧,则二面角的平面角=
2、求空间距离问题:
构成空间的点、线、面之间有七种距离,这里着重介绍点面距离的求法,象异面直线间的距离、线面距离;面面距离都可转化为点面距离来求.
(1)求点面距离:
法一、设是平面的法向量,在内取一点B, 则 A到的距离
法二、设于O,利用和点O在内的向量表示,可确定点O的位置,从而求出.
(2)求异面直线的距离:
法一、找平面使且,则异面直线a、b的距离就转化为直线a到平面的距离,又转化为点A到平面的距离.
法二、在a上取一点A, 在b上取一点B, 设、分别为异面直线a、b的方向向量,求(,),则异面直线a、b的距离(此方法移植于点面距离的求法).
三、例题讲解:
例1.如图,在棱长为2的正方体中,E、F分别是棱的中点.
(Ⅰ)求异面直线所成的角;
(II)求和面EFBD所成的角;
(III)求到面EFBD的距离
解:略
设计说明:1.例1,首先选择以一个容易建立空间直角坐标系的多面体―――正方体为载体,来说明空间角和距离的向量求法易于学生理解.
2.解决(1)后,可让学生进一步求这两条异面直线的距离,并让学生体会一下:如果用传统方法恐怕很难(不必多讲,高中对公垂线的作法不作要求).
3.完成这3道小题后,总结:对于易建立空间直角坐标系的立几题,无论求角、距离还是证明平行、垂直(是前者的特殊情况),都可用向量方法来解决,
向量方法可以人人学会,它程序化,不需技巧.
例2.如图,三棱柱中,已知A BCD是边长为1的正方形,四边形
是矩形,
(Ⅰ)若=1,求直线AB到面的距离.
(II) 试问:当的长度为多少时,二面角
的大小为
解:(略)
设计说明:1.通过(Ⅰ),复习线面距离转化为点面距离再转化为一向量在一向量(法向量)投影的绝对值的解题思路与方法.
2.通过(II),复习面面角转化为两向量的夹角或其补角的方法,也可借此机会说明为什么这两个角相等或互补,就没有其他情况.
四、课堂练习:
P107练习题:1、2
五、小结:
与学生一同归纳小结本节课的重点知识点。(略)
六、作业布置:
课本习题、导航练习题。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
