中考数学思想
图片预览







文档简介
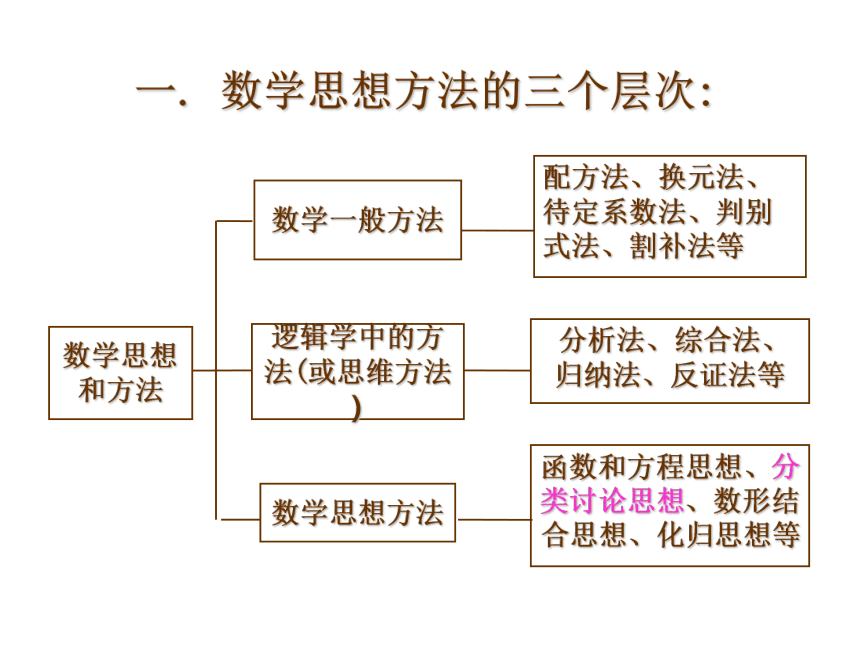
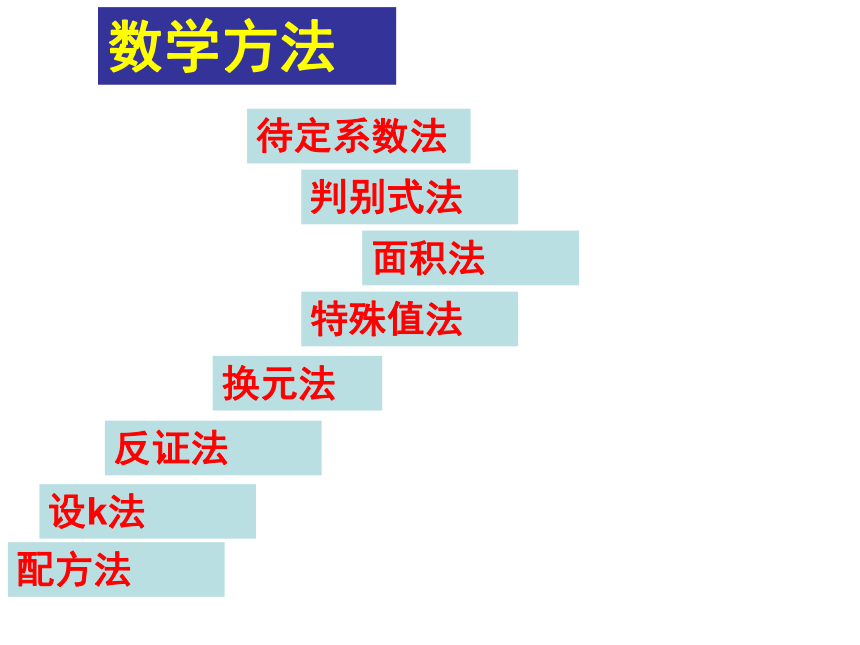
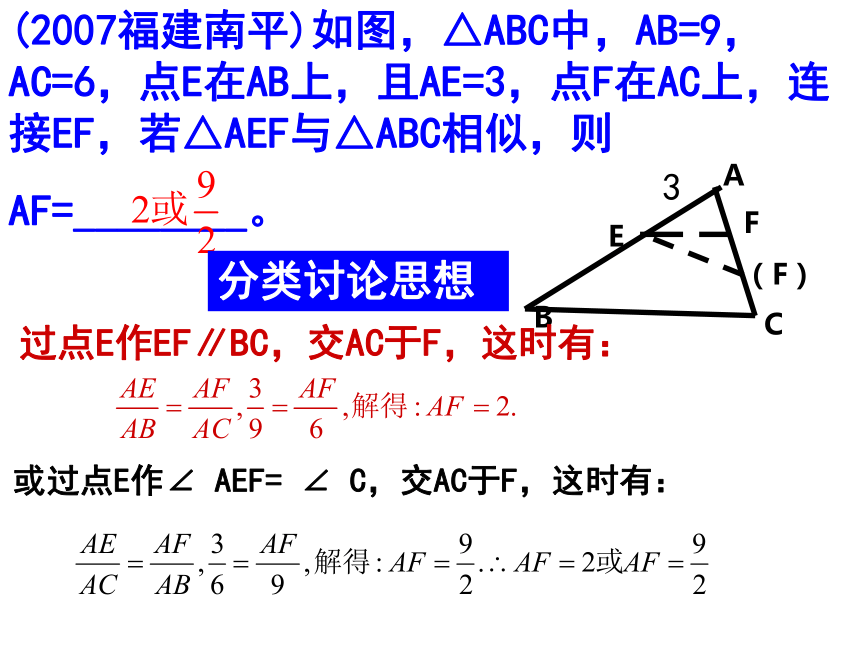
课件58张PPT。一. 数学思想方法的三个层次: 数学就是这样一种东西:她提醒你有无形的灵魂,她赋予她所发现的真理以生命;她唤起心神,澄净智能;她给我们的内心思想添辉;她涤尽我们有生以来的蒙昧与无知。数学方法换元法待定系数法特殊值法判别式法面积法反证法设k法配方法数学思想分类讨论思想方程与不等式的思想函数思想转化思想(化归思想)数形结合思想整体思想初中阶段常用到的数学思想方法有:数形结合思想、分类讨论思想、转化思想、函数与方程思想、建立数学模型的思想等.(2009乐山)若实数a,b在数轴上对应的点的位置如下图,数形结合思想(2007福建南平)如图,△ABC中,AB=9,AC=6,点E在AB上,且AE=3,点F在AC上,连接EF,若△AEF与△ABC相似,则
AF=________。ABCE过点E作EF∥BC,交AC于F,这时有:或过点E作∠ AEF= ∠ C,交AC于F,这时有:3分类讨论思想分类讨论思想(2009.安徽)已知二次函数的图像经过原点、 ,且图像与x轴的另一个交点到原点的距离为1,则二次函数的
解析式为_________________________.3、关键:根据折叠实现等量转化。(2)根据相似比得方程。(1)根据勾股定理得方程。4、基本方法:构造方程
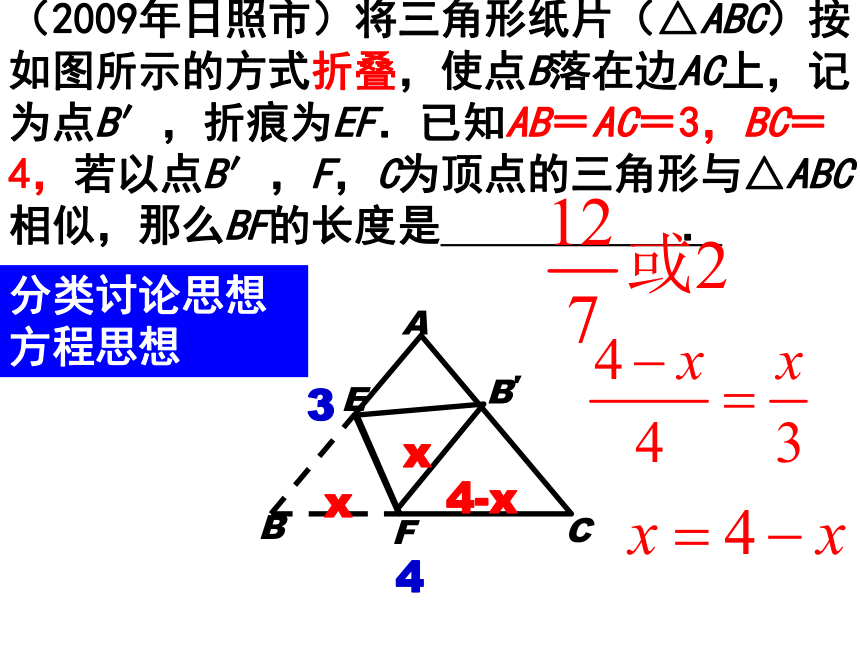
折叠问题1、两手都要抓:重视“折”,关注“叠”。2、本质:轴对称(全等性,对称性)。(2009年日照市)将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是 .xx4-x34分类讨论思想
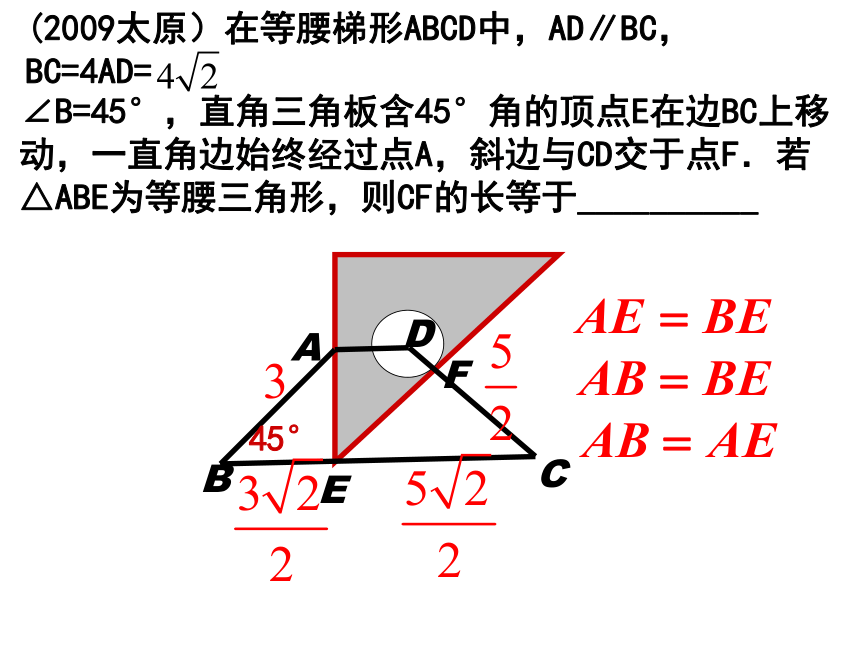
方程思想(2009太原)在等腰梯形ABCD中,AD∥BC,
BC=4AD=∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于__________ DBCAEF45°(2009太原)在等腰梯形ABCD中,AD∥BC,
BC=4AD=∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于__________ DBCAEF45°67.5°67.5°67.5°(2009太原)在等腰梯形ABCD中,AD∥BC,
BC=4AD=∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于__________ DBCAEF45°45°(2009重庆綦江)如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A.(4,0) B.(1.0) D.(2,0)BPP 课外思考中考中多解情况作为重点考察
填空题中如果没有给出图形,有两解的可能性很大(2009牡丹江)已知:Rt△ABC中,∠C=90o,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边中点D处,折痕交另一直角边于E,交斜边于F,tan∠CDE=_____?(2009牡丹江)已知:Rt△ABC中,∠C=90o,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边中点D处,折痕交另一直角边于E,交斜边于F,tan∠CDE=_____?4x6-x6-x(6-x)2=x2+42,已知:Rt△ABC中,∠C=90o,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边中点D处,折痕交另一直角边于E,交斜边于F,tan∠CDE=(8-x)2=x2+32,x38-x8-x(2009年黄冈市)在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于_____________度.50°50°40°拓展训练数形结合思想
分类讨论思想(2009呼和浩特)在等腰△ABC中,AB=AC,
一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A.7 B.11 C.7或11 D.7或10xy0.5y0.5y(2009朝阳)已知菱形的一个内角为60°,一条对角线的长为则另一条对角线的长为____________.30°30°(2008哈尔滨)菱形ABCD的边长为6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则△MCB∽△MAE(2008南昌)如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,(1)求证:B′E=BF;(2)设AE=a,AB=b, BF=c,试猜想a、b、c之间的一种关系,并给予证明.规律:折叠意味着全等
角平分线+平行线
可形成等腰三角形(2008陕西)Rt△ABC中,∠ACB=90°,
AC=5,CB=12,AD是△ABC的角平分线,
(1)求证AC=AE
(2)求△ACD外接圆的半径。XX12-X558方程思想晚上,小亮走在大街上,他发现:当他站在大街两旁的两盏路灯之间,并且发现被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3m,左边的影子长为1.5m,又知,自己身高1.80m,两盏路灯的高相同,两盏路灯之间的距离为12m,求路灯的高。(答案:6.6m)方程思想·北师大版x34-xx32x2+22=(4-x)2
x2+4=x2-8x+16
8x=12
x=1.5方程思想⊙O中,半径OB⊥半径OA于点O,
以OB为直径作⊙O1中, AD切⊙O1于点D,⊙O1的半径为r,求AO1,DE(2008杭州)r2rrx2r2x-r(2009年泸州)如图1,在边长为1的等边△ABC中,中线AD与中线BE相交于点O,则OA长度
为 .x2x方法2:(2x)2-x2=0.52(2009.兰州)已知抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点(-1,y1)(2,y2)试比较y1和y2的大小:y1_____y2.>∵a>0,可取a=1,∵对称轴是直线x=1,
∴满足该条件的抛物线解析式可以为:
y=(x-1)2,
把x=-1,x=2分别带入y=(x-1)2得:
y1=4,y2=1,
∵4>1,∴y1>y2 。特殊值法正方形ABCD中FD切半圆与点F,求△ADE与直角梯形EBCD周长之比(2008杭州)11E特殊值法:设正方形边长为1
则△ADE的周长为311设EF为x,则
(1+x)2=(1-x)2+12
x=0.25x直角梯形EBCD周长为:3.53:3.5=6:71-x则图中阴影部分的面积与正方形ABCD的面积之比是________(2008无锡)正方形ABCD,(2008重庆)正方形纸片ABCD,折叠该纸片,使点A恰好与BD上的点F重合,折痕为DE下列结论① ∠AGD=112.5° ②tan ∠AED=2
③S△AGD= S△OGD ④四边形AEFG是菱形
⑤BE=2OG正确的序号是______________22.5°45°112.5°67.5°1①④⑤(2008.福州)已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2008的值为( )整体思想把(m,0)代入抛物线y=x2-x-1得:
m2-m-1=0,m2-m=1
∴m2-m+2008=(m2-m)+2008
=1+2008
=2009(2009江苏)若3a2-a-2=0,
则5+2a-6a2=___________∵3a2-a-2=0,
∴ 3a2-a=2
∴5+2a-6a2
=5+2(a-3a2)
=5-2×2
=1若(x+y)(1-x-y)+6=0,则x+y=___设x+y=a,则原式可化为
a(1-a)+6=0
-a2+a+6=0
a2-a-6=0
(a-3)(a+2)=0-2或3换元法如果x2+x-1=0,那么代数式
x3+2x2-7的值为___∵x2+x-1=0 ,∴ x2+x=1
则x3+2x2-7
=x3+x2+x2-7
=x(x2+x)+x2-7
=x+x2-7
=1-7
=-6例:已知一次函数的图象经过点(3,5)与
(-4,-9).求这个一次函数的解析式 解:设这个一次函数的解析式为y=kx+b.∵y=kx+b的图象过点(3,5)与(-4,-9).∴这个一次函数的解析式为y=2x-1设代解待定系数法.答已知二次函数的图象的顶点是(2,3)且经过点(3,1),求这个二次函数的解析式。解:∵该抛物线的顶点为(2,3),
∴设 y=a(x-2)2+3∵这段抛物线经过点(3,1)∴ 1=a(3-2)2+3解得:a=-2∴抛物线的解析式为:y=-2(x-2)2+3=-2x2+8x-5两个相似三角形的一对对应边分别是 35 cm和14cm, 它们的周长相差42cm,求这两
个三角形的面积。设k法解:∵相似三角形对应边的比为35:14=5:2∴相似三角形面积的比为25:4
设大三角形的面积为25k,小三角形的
面积为4k,25k-4k=42,21k=42,k=2,
∴25k=50,4k=8,
答:这两个三角形的面积分别为50、8(北京2008)Rt△ABC中∠C=900,∠CBD=∠A,
(1)判断直线BD与⊙0的位置关系,并证明结论
(2)若AD:AO=8:5,BC=2,求BD的长(2)过点O作OF⊥CA于点F,
∵∠C=900
∴ ∠OFD=∠C
∵ OA=OD
∴ ∠1=∠A,
又∵∠CBD=∠A
∴ ∠1=∠CBD
∴△OFD∽△DCB
∵AD:AO=8:5
∴设AD=8k,AO=5k,
则DF=4k,OD=5k,
F(北京2008)Rt△ABC中∠C=900,∠CBD=∠A,
(1)判断直线BD与⊙0的位置关系,并证明结论
(2)若AD:AO=8:5,BC=2,求BD的长(2)连接DE,∵AE是直径,
∴∠ADE=900
∵AD:AO=8:5
∴设AD=8k,AO=5k,
则AE=10k∵∠CBD=∠A如何求直角三角形
斜边上的高?Rt△ABC的两直角边为6、8,
则该直角三角形斜边上的高为______面积法如何求直角三角形
斜边上的高?Rt△ABC的两直角边为6、8,
则该直角三角形斜边上的高为______(2009年新疆)如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是a,b
斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.方法一,解:(1)如图证明:∵大正方形的面积
表示为(a+b)2,
大正方形的面积也可表示为即直角三角形两直角边的平方和等于斜边的平方. 方法二,解:(1)如图证明:∵大正方形的面积
表示为c2,
大正方形的面积也可表示为即直角三角形两直角边的平方和等于斜边的平方. (2009安徽)如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰
能拼成一个矩形(非正方形).
(1)画出拼成的矩形的简图;
(2)求 的值.(2)由拼图前后的面积相等得:因为y≠0,整理得:(负值不合题意,舍去)一正五边形纸片沿其对称轴对折,旋转放置,做成科学方舟模型.如图所示,该正五边形的边心距OB长为 AC为科学方舟船头A到船底的距离, 请你计算 (2009芜湖) a0.5aa面积法EF割
补
面
积
法△ABC边长分别为
求△ABC面积割
补
面
积
法△ABC边长分别为
求△ABC面积割
补
面
积
法△ABC边长分别为
求△ABC面积16.(2009年清远)如图,已知AB是⊙ O的
直径,过点O作弦BC的平行线,交过点A的切
线AP于点P,,连结AC
(1)求证: △ABC∽△POA
(2)若OB=2,OP=3.5,求BC的长。规律:有的题有多问时,
一般下一问的解答
要用到第1问的结论,
如果第1问不会的话,
可选择跳步解答(2)解:∵△ABC∽△POA在证明等腰三角形时,常需应用作辅助线构造全等三角形,进而应用等腰三角形的性质为题目服务,常用的构造方法有:
①“角平分线+平行线”构造等腰三角形;
②“角平分线+垂线”构造等腰三角形;
③用“垂直平分线”构造等腰三角形;
④用“三角形中角的2倍关系”构造等腰三角形
AF=________。ABCE过点E作EF∥BC,交AC于F,这时有:或过点E作∠ AEF= ∠ C,交AC于F,这时有:3分类讨论思想分类讨论思想(2009.安徽)已知二次函数的图像经过原点、 ,且图像与x轴的另一个交点到原点的距离为1,则二次函数的
解析式为_________________________.3、关键:根据折叠实现等量转化。(2)根据相似比得方程。(1)根据勾股定理得方程。4、基本方法:构造方程
折叠问题1、两手都要抓:重视“折”,关注“叠”。2、本质:轴对称(全等性,对称性)。(2009年日照市)将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是 .xx4-x34分类讨论思想
方程思想(2009太原)在等腰梯形ABCD中,AD∥BC,
BC=4AD=∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于__________ DBCAEF45°(2009太原)在等腰梯形ABCD中,AD∥BC,
BC=4AD=∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于__________ DBCAEF45°67.5°67.5°67.5°(2009太原)在等腰梯形ABCD中,AD∥BC,
BC=4AD=∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于__________ DBCAEF45°45°(2009重庆綦江)如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A.(4,0) B.(1.0) D.(2,0)BPP 课外思考中考中多解情况作为重点考察
填空题中如果没有给出图形,有两解的可能性很大(2009牡丹江)已知:Rt△ABC中,∠C=90o,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边中点D处,折痕交另一直角边于E,交斜边于F,tan∠CDE=_____?(2009牡丹江)已知:Rt△ABC中,∠C=90o,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边中点D处,折痕交另一直角边于E,交斜边于F,tan∠CDE=_____?4x6-x6-x(6-x)2=x2+42,已知:Rt△ABC中,∠C=90o,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边中点D处,折痕交另一直角边于E,交斜边于F,tan∠CDE=(8-x)2=x2+32,x38-x8-x(2009年黄冈市)在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于_____________度.50°50°40°拓展训练数形结合思想
分类讨论思想(2009呼和浩特)在等腰△ABC中,AB=AC,
一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A.7 B.11 C.7或11 D.7或10xy0.5y0.5y(2009朝阳)已知菱形的一个内角为60°,一条对角线的长为则另一条对角线的长为____________.30°30°(2008哈尔滨)菱形ABCD的边长为6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则△MCB∽△MAE(2008南昌)如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,(1)求证:B′E=BF;(2)设AE=a,AB=b, BF=c,试猜想a、b、c之间的一种关系,并给予证明.规律:折叠意味着全等
角平分线+平行线
可形成等腰三角形(2008陕西)Rt△ABC中,∠ACB=90°,
AC=5,CB=12,AD是△ABC的角平分线,
(1)求证AC=AE
(2)求△ACD外接圆的半径。XX12-X558方程思想晚上,小亮走在大街上,他发现:当他站在大街两旁的两盏路灯之间,并且发现被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3m,左边的影子长为1.5m,又知,自己身高1.80m,两盏路灯的高相同,两盏路灯之间的距离为12m,求路灯的高。(答案:6.6m)方程思想·北师大版x34-xx32x2+22=(4-x)2
x2+4=x2-8x+16
8x=12
x=1.5方程思想⊙O中,半径OB⊥半径OA于点O,
以OB为直径作⊙O1中, AD切⊙O1于点D,⊙O1的半径为r,求AO1,DE(2008杭州)r2rrx2r2x-r(2009年泸州)如图1,在边长为1的等边△ABC中,中线AD与中线BE相交于点O,则OA长度
为 .x2x方法2:(2x)2-x2=0.52(2009.兰州)已知抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点(-1,y1)(2,y2)试比较y1和y2的大小:y1_____y2.>∵a>0,可取a=1,∵对称轴是直线x=1,
∴满足该条件的抛物线解析式可以为:
y=(x-1)2,
把x=-1,x=2分别带入y=(x-1)2得:
y1=4,y2=1,
∵4>1,∴y1>y2 。特殊值法正方形ABCD中FD切半圆与点F,求△ADE与直角梯形EBCD周长之比(2008杭州)11E特殊值法:设正方形边长为1
则△ADE的周长为311设EF为x,则
(1+x)2=(1-x)2+12
x=0.25x直角梯形EBCD周长为:3.53:3.5=6:71-x则图中阴影部分的面积与正方形ABCD的面积之比是________(2008无锡)正方形ABCD,(2008重庆)正方形纸片ABCD,折叠该纸片,使点A恰好与BD上的点F重合,折痕为DE下列结论① ∠AGD=112.5° ②tan ∠AED=2
③S△AGD= S△OGD ④四边形AEFG是菱形
⑤BE=2OG正确的序号是______________22.5°45°112.5°67.5°1①④⑤(2008.福州)已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2008的值为( )整体思想把(m,0)代入抛物线y=x2-x-1得:
m2-m-1=0,m2-m=1
∴m2-m+2008=(m2-m)+2008
=1+2008
=2009(2009江苏)若3a2-a-2=0,
则5+2a-6a2=___________∵3a2-a-2=0,
∴ 3a2-a=2
∴5+2a-6a2
=5+2(a-3a2)
=5-2×2
=1若(x+y)(1-x-y)+6=0,则x+y=___设x+y=a,则原式可化为
a(1-a)+6=0
-a2+a+6=0
a2-a-6=0
(a-3)(a+2)=0-2或3换元法如果x2+x-1=0,那么代数式
x3+2x2-7的值为___∵x2+x-1=0 ,∴ x2+x=1
则x3+2x2-7
=x3+x2+x2-7
=x(x2+x)+x2-7
=x+x2-7
=1-7
=-6例:已知一次函数的图象经过点(3,5)与
(-4,-9).求这个一次函数的解析式 解:设这个一次函数的解析式为y=kx+b.∵y=kx+b的图象过点(3,5)与(-4,-9).∴这个一次函数的解析式为y=2x-1设代解待定系数法.答已知二次函数的图象的顶点是(2,3)且经过点(3,1),求这个二次函数的解析式。解:∵该抛物线的顶点为(2,3),
∴设 y=a(x-2)2+3∵这段抛物线经过点(3,1)∴ 1=a(3-2)2+3解得:a=-2∴抛物线的解析式为:y=-2(x-2)2+3=-2x2+8x-5两个相似三角形的一对对应边分别是 35 cm和14cm, 它们的周长相差42cm,求这两
个三角形的面积。设k法解:∵相似三角形对应边的比为35:14=5:2∴相似三角形面积的比为25:4
设大三角形的面积为25k,小三角形的
面积为4k,25k-4k=42,21k=42,k=2,
∴25k=50,4k=8,
答:这两个三角形的面积分别为50、8(北京2008)Rt△ABC中∠C=900,∠CBD=∠A,
(1)判断直线BD与⊙0的位置关系,并证明结论
(2)若AD:AO=8:5,BC=2,求BD的长(2)过点O作OF⊥CA于点F,
∵∠C=900
∴ ∠OFD=∠C
∵ OA=OD
∴ ∠1=∠A,
又∵∠CBD=∠A
∴ ∠1=∠CBD
∴△OFD∽△DCB
∵AD:AO=8:5
∴设AD=8k,AO=5k,
则DF=4k,OD=5k,
F(北京2008)Rt△ABC中∠C=900,∠CBD=∠A,
(1)判断直线BD与⊙0的位置关系,并证明结论
(2)若AD:AO=8:5,BC=2,求BD的长(2)连接DE,∵AE是直径,
∴∠ADE=900
∵AD:AO=8:5
∴设AD=8k,AO=5k,
则AE=10k∵∠CBD=∠A如何求直角三角形
斜边上的高?Rt△ABC的两直角边为6、8,
则该直角三角形斜边上的高为______面积法如何求直角三角形
斜边上的高?Rt△ABC的两直角边为6、8,
则该直角三角形斜边上的高为______(2009年新疆)如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是a,b
斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.方法一,解:(1)如图证明:∵大正方形的面积
表示为(a+b)2,
大正方形的面积也可表示为即直角三角形两直角边的平方和等于斜边的平方. 方法二,解:(1)如图证明:∵大正方形的面积
表示为c2,
大正方形的面积也可表示为即直角三角形两直角边的平方和等于斜边的平方. (2009安徽)如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰
能拼成一个矩形(非正方形).
(1)画出拼成的矩形的简图;
(2)求 的值.(2)由拼图前后的面积相等得:因为y≠0,整理得:(负值不合题意,舍去)一正五边形纸片沿其对称轴对折,旋转放置,做成科学方舟模型.如图所示,该正五边形的边心距OB长为 AC为科学方舟船头A到船底的距离, 请你计算 (2009芜湖) a0.5aa面积法EF割
补
面
积
法△ABC边长分别为
求△ABC面积割
补
面
积
法△ABC边长分别为
求△ABC面积割
补
面
积
法△ABC边长分别为
求△ABC面积16.(2009年清远)如图,已知AB是⊙ O的
直径,过点O作弦BC的平行线,交过点A的切
线AP于点P,,连结AC
(1)求证: △ABC∽△POA
(2)若OB=2,OP=3.5,求BC的长。规律:有的题有多问时,
一般下一问的解答
要用到第1问的结论,
如果第1问不会的话,
可选择跳步解答(2)解:∵△ABC∽△POA在证明等腰三角形时,常需应用作辅助线构造全等三角形,进而应用等腰三角形的性质为题目服务,常用的构造方法有:
①“角平分线+平行线”构造等腰三角形;
②“角平分线+垂线”构造等腰三角形;
③用“垂直平分线”构造等腰三角形;
④用“三角形中角的2倍关系”构造等腰三角形
同课章节目录
